Consensus control of feedforward nonlinear multi-agent systems:a time-varying gain method

Hanfeng Li·Xianfu Zhang·Weihao Pan

Abstract In this paper, the leader–follower consensus of feedforward nonlinear multi-agent systems is achieved by designing the distributed output feedback controllers with a time-varying gain.The agents dynamics are assumed to be in upper triangular structure and satisfy Lipschitz conditions with an unknown constant multiplied by a time-varying function.A time-varying gain, which increases monotonously and tends to infinity, is proposed to construct a compensator for each follower agent.Based on a directed communication topology,the distributed output feedback controller with a time-varying gain is designed for each follower agent by only using the output information of the follower and its neighbors.It is proved by the Lyapunov theorem that the leader–follower consensus of the multi-agent system is achieved by the proposed consensus protocol.The effectiveness of the proposed time-varying gain method is demonstrated by a circuit system.

Keywords Consensus control·Nonlinear multi-agent systems·Time-varying gain·Output feedback

1 Introduction

The cooperative control problem of multi-agent systems has been widely considered [1,2]. This is primarily due to their significant applications in many industrial areas such as microgrids and networked mobile robots[3,4].

Leader–follower consensus, as an essential problem in the research of multi-agent systems,is to construct the distributed protocol, such that the signals of the followers can track the signals of the leader.The single integrator systems were considered in [5], and the double integrator systems were investigated in [6]. There exist also many research results on linear systems,such as[7–9].

Recently, some interesting research works have been received for nonlinear multi-agent systems. The secondorder systems were studied in [10], and the high-order systems were considered in [11]. It is widely known that the controller design of nonlinear systems with triangular structure is a meaningful problem [12]. Some results were obtained on multi-agent systems subject to the lower triangular structure; see [13–15]. Hua et al. [13] illustrated that the backstepping method was a powerful tool for solving the consensus problem of multi-agent systems. In [14,15],with the help of the state transformation, the consensus problem was transformed into the control gain constructing problem, which avoided effectively the complicated iterativeprocess.Moreover,theconsensusproblemofmulti-agent systems with the upper triangular structure was investigated in[16,17].However,the controller designed in[16]for each followeragentwasrelatedtotheobserverstateinformationof its neighbors.Li et al.[17]presented a much more restrictive condition requiring the agents dynamics to satisfy Lipschitz conditions with a known constant.

The time-varying gain method has been utilized to solve the convergence problem of the single feedforward nonlinear system. Based on the system state information or observer state information, the time-varying gain was designed in[18,19],respectively.The time-varying gain can effectively deal with the influences of the time-varying nonlinear terms or unknown parameters, and ensure the convergence performance of the states. It should be pointed out that the time-varying gain constructed in [18,19] was unbounded.Different from the forwarding design method, the timevarying gain method transforms the controller design problem into that of establishing a time-varying function, thus avoiding the complicated iterative process[16].

Generally speaking, it is difficult to construct a stabilizing controller for feedforward systems with the time-varying nonlinear terms. The existing results mainly focus on constructing the regulating controller by introducing a timevarying gain [18,19]. In this case, the convergence speed of the system states and the time-varying gain need to be considered.Therefore,this greatly restricts the time-varying characteristics of nonlinear terms,and requires that the timevarying gain cannot have a fast growth rate. On the other hand, for time-varying multi-agent systems, how to effectively improve the convergence speed of leader–follower consensus is also a challenging question.To effectively overcome these difficulties,this paper designs a new distributed time-varying gain controllers for feedforward multi-agent systems. By giving the relationship about the convergence speed between consensus errors and the time-varying gain,this paper effectively solves the consensus control problem of feedforward multi-agents with the time-varying characteristic.

In this paper,a new time-varying gain method is proposed toachievetheleader–followerconsensusoffeedforwardnonlinear multi-agent systems. There are two difficulties that we are facing. The first is that the considered system possesses an unknown constant.How to eliminate the influence of unknown constant is a difficulty. The second is that the proposed topology is directed and fixed,and it is difficult to decrease the information communication. The main contributions are summarized as follows.First,a new time-varying gain is established to determine the distributed output feedback controllers for the concerned multi-agent systems.The assumption on the agents dynamics is more general, since Lipschitz conditions contain a continuous time-varying function, which greatly relaxes the nonlinear characteristics of[15,17]. Second, the distributed controller is designed for each follower agent by only using the output information of the follower and its neighbors. Different from [14,16], the compensator state is not required to be transmitted, which decreases the information communication.Last but not least,an appropriate state transformation is proposed to introduce a Hurwitz matrix, which is crucial to analyze the leader–follower consensus of multi-agent systems. Therefore, the developed distributed protocol with a time-varying gain is a novel method to solve the consensus problem of multi-agent systems.

The rest of the paper is organized as follows.In Sect.2,preliminaries and problem formulation are provided. In Sect. 3, one presents the main results, including the design process of output feedback controllers with a time-varying gain,and the analysis process of leader–follower consensus.Section 4 illustrates a simulation example,and Sect.5 draws the conclusion.

2 Preliminaries and problem formulation

In this section,we provide some symbolic explanations and basic concepts related to the graph theory, as well as the system model and control objective in this paper.

2.1 Notations

Throughout this paper,the following notations can be given[19,20].

2.2 Graph theory

In this paper,the following graph theory can be introduced[15,21].

2.3 Problem formulation

In this paper,a group ofN+1 agents consisting of a leader andNfollowers are considered. The leader is indexed by 0,and the followers are referred as 1,2,...,N.The agents dynamics are given as follows:

Remark 1The agents dynamics of system (1) possess the upper triangular structure [22]. The consensus control of multi-agent systems with the upper triangular structure is a hot research topic [16,17]. Many actual systems, such as circuit systems with special structure [19] and multiple planar aircraft models [23], can be transformed into feedforward nonlinear multi-agent systems through appropriate transformations.Compared with the assumption of[16,17],the condition(2)in this paper is more general due to the fact that Lipschitz conditions contain an unknown constantθand the continuous time-varying function ln(t+1).In[16],the consensus problem for system(1)satisfying(2)without the function ln(t+1)was solved. Moreover, the time-varying gain designed in[17]was bounded,which may bring about conservativeness in handling the unknown constantθand the function ln(t+1).Assumption 2 is a standard condition in achieving the consensus control as in[14,15].

3 Main results

In this section, one gives the main results, including the construct process of distributed output feedback controllers with a time-varying gain,and the analysis process of leader–follower consensus.

3.1 Design of distributed output feedback controllers with a time-varying gain

By designing the compensators with the state ˆxiand timevarying gainρfor system (1), a new distributed consensus protocol can be established.

Let

whereα1is a positive design constant,to be determined later.

Remark 2The information transmission between neighbors in the multi-agent system is required.The distributed control strategy mentioned in this paper not only achieves the leader–follower consensus objective,but also effectively reduces the information transmission. The distributed output feedback controller(8)for each agent only needs the output information of its neighbors.This is mainly due to the introduction of the output consensus errorεiin the compensator(4)and the time-varying gain(5).Different from[14,16],where the controller contained the observer state information of its neighbors,the consensus protocol proposed in this paper can obviously reduce the information transmission.

Remark 3For the time-varying nonlinear terms in the logarithmic form,this paper proposes a time-varying gain in the form of a linear function.When the time is sufficiently large,the time-varying gain controllers can effectively restrain the unknown constantθand the time-varying function ln(t+1).

However,the time-varying gainρneeds to consider the convergence speed of the consensus errors. When the gainρincreases too fast, it may cause the controller to converge to zero, but the consensus errors do not converge to zero.Therefore,by introducing the design parameterα1,both the consensus errors and the controllers can converge to zero.

3.2 Leader–follower consensus via distributed output feedback controllers

Based on an appropriate technique, the leader–follower consensus is achieved by the distributed output feedback controllers with a time-varying gain.

Theorem 1Under Assumptions1and2,the following distributed output feedback controllers with a time-varying gain:

ProofThe proof is similar for Theorem 1,and it is omitted to avoid repetition.■

Remark 6In Theorem 2,to solve the influence of unknown constantθ,the gainρwith the logarithmic form is constructed.It is shown that the gainρincrease monotonously and tends to infinity.The growth rate of the gainρis slower thanthegrowthrateofalinearfunction,whichcaneffectively improve the convergence speed of consensus errors.The case that without the function ln(t+1)was solved in[16]by the time-varying gain method. However, the time-varying gain designed in[16]caused a slower consensus speed.Different from[16],the gainρwith the logarithmic form is constructed in (22), such that the convergence speed of the consensus errors is not too slow.

4 A simulation example

To demonstrate the effectiveness of the proposed consensus protocol,a simulation example can be provided.

Example 1Thenonlinearliquid-levelcontrolresonantcircuit systems as agents is investigated as[19,25]

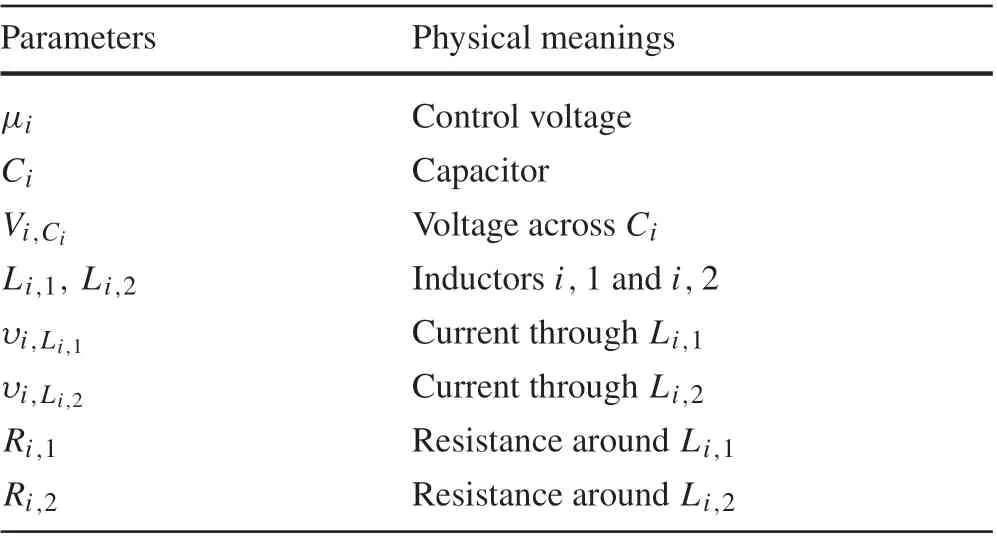
Table 1 Physical meanings of parameters

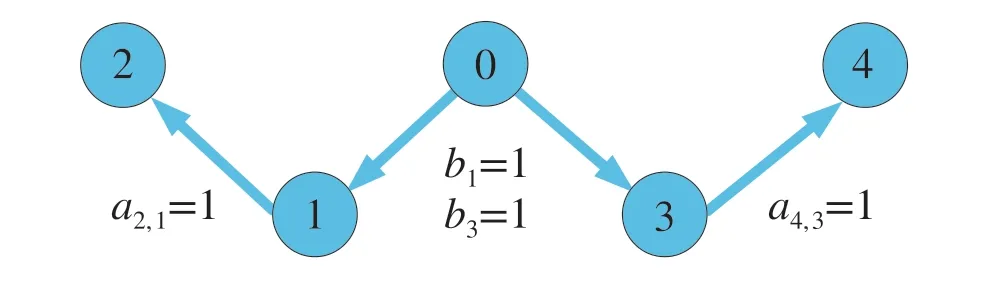
Fig.1 The communication topology

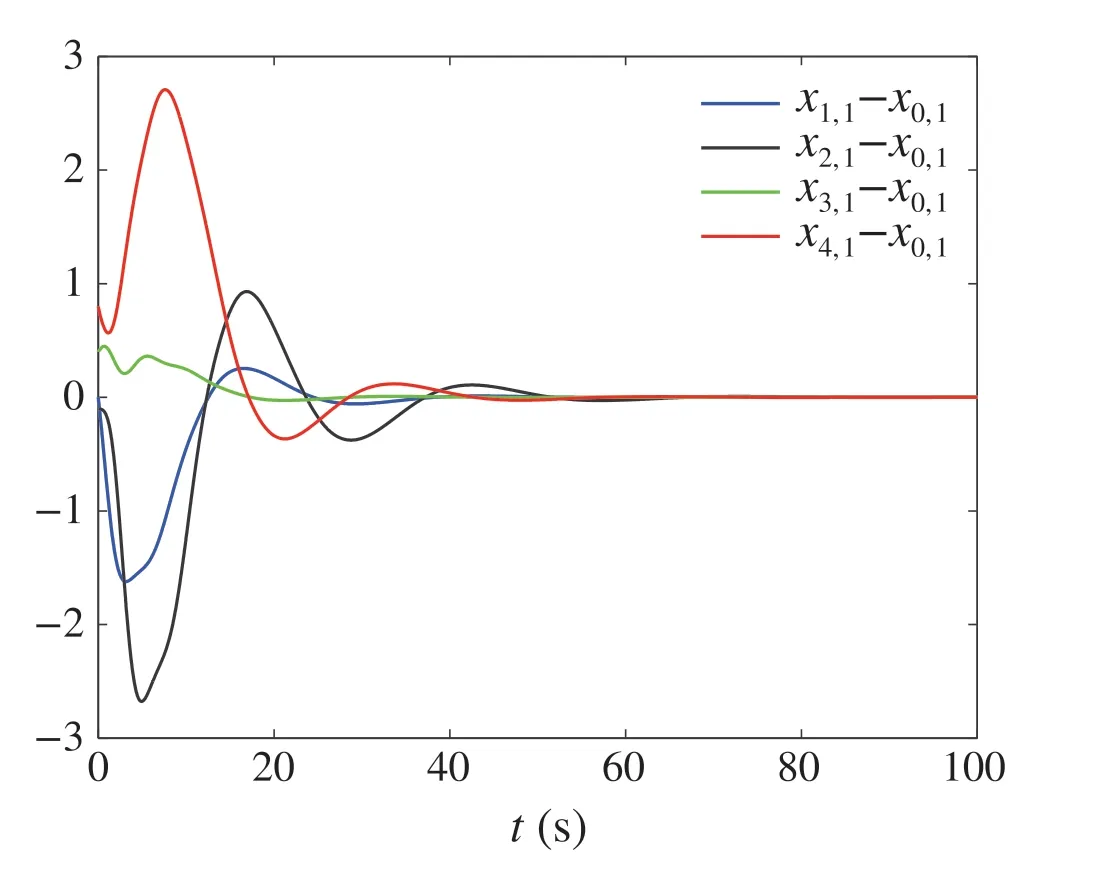
Fig.2 The responses of xi,1-x0,1,i =1,2,3,4

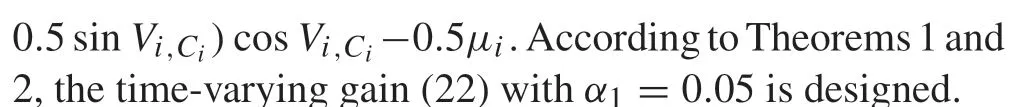
Figures 2,3,4 and 5 illustrate the signals responses of the system with initial conditionx0,1(0)=x1,1(0)=x2,3(0)=-0.5, x0,2(0)=x3,2(0)= 0.5, x0,3(0)=x4,2(0)= -0.4,x1,2(0)=x4,3(0)= 0.1, x1,3(0)= -0.7, x2,1(0)= -0.6,x2,2(0)= 0.6, x3,1(0)= -0.1, x3,3(0)= -0.3, x4,1(0)=0.3,andui(0)= ˆxi,1(0)= ˆxi,2(0)= ˆxi,3(0)= 0, i=1,2,3,4.

By Figs.2,3 and 4,it can be observed that all the states of the followers track the states of the leader.Figure 5 shows the responses of the controllers.

Remark 7Through the example(23),one can know that the designed time-varying gain can effectively adjust the convergence speed of consensus errors and distributed output feedback controllers. Compared with the examples in [14]and[16],the distributed output feedback controller(8)for theith follower agent may save the communication bandwidth,since it only needs the output information of the follower and its neighbors.Moreover,different from[17],the characteristic of the concerned system is more obvious, since the nonlinear terms contain the unknown constant.

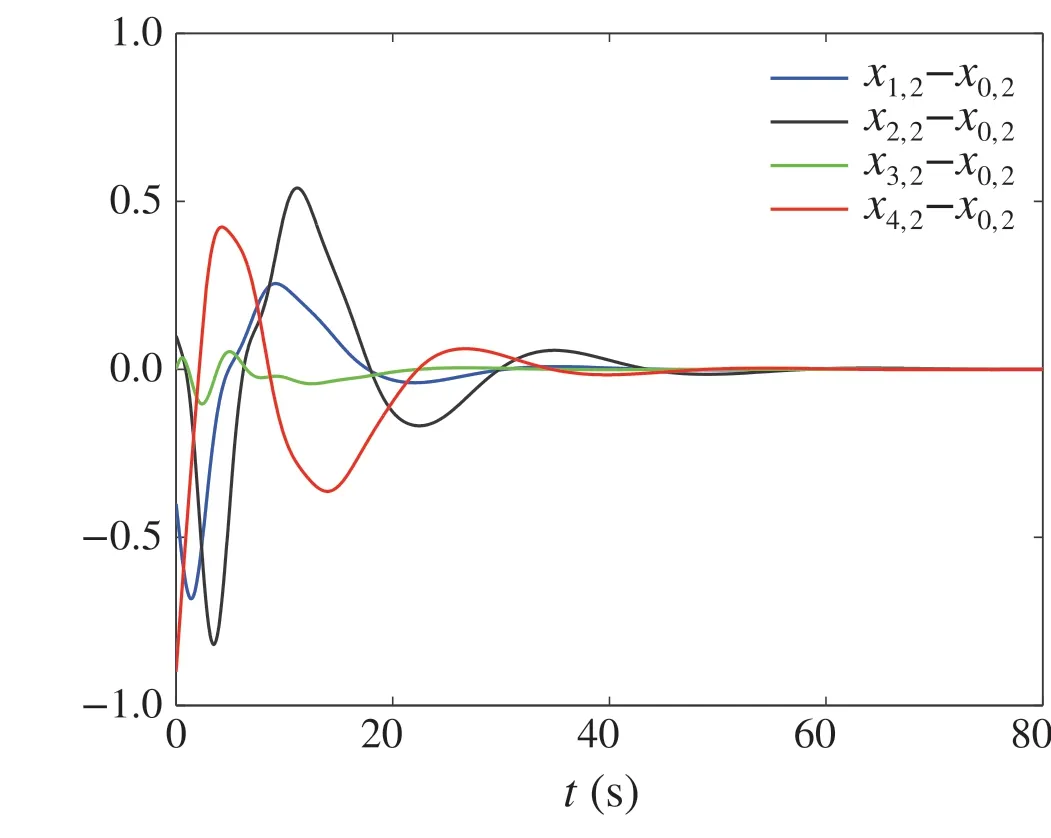
Fig.3 The responses of xi,2-x0,2,i =1,2,3,4

Fig.4 The responses of xi,3-x0,3,i =1,2,3,4

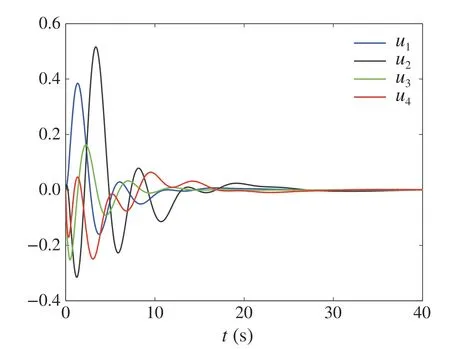
Fig.5 The responses of ui,i =1,2,3,4

5 Conclusions

In this paper, we have achieved the leader–follower consensus of feedforward nonlinear multi-agent systems via designing distributed controllers with a time-varying gain.The consensus protocol has been proposed without resorting to the celebrated forwarding design method, which has avoided the complex iterative algorithm.An appropriate state transformation has been proposed to introduce a Hurwitz matrix,which is crucial to analyze the leader–follower consensus of multi-agent systems. A simulation example has been provided to show the effectiveness of the proposed timevarying gain method.The future research is to construct the distributed controllers by the time-varying gain method for feedforward nonlinear multi-agent time-delay systems.