Safety stabilization of switched systems with unstable subsystems

Lijun Long·Yiguang Hong

Abstract This paper is concerned with the problem of safety stabilization for switched systems where the solvability of the problem under study for individual subsystems is not assumed.A new state-dependent switching strategy with guaranteed dwell-time for switched systems is constructed,and a sufficient condition for absence of Zeno behavior is derived.Also,a novel switched control design method is proposed to simultaneously guarantee the safety of the switched closed-loop system and stabilize the system based on the union of a common barrier function and a single Lyapunov function,which effectively handles the conflict between safety and stability objectives.Finally,two examples are presented to demonstrate the effectiveness of the proposed design approach.

Keywords Safety stabilization·Switched systems·Common barrier function·Single Lyapunov function·State-dependent switching

1 Introduction

The safety-critical control with many applications, such as self-driving cars, autonomous mobile robots and industrial manipulators[1–3],is conducted to guarantee that the system states stay in a safe set[4,5].Recently,it has attracted much attention in[6–8].To study such a problem,safety verification and safe control design using(control)barrier functions have been widely and successfully employed for nonlinear systems [9–12]. However, it is difficult to simultaneously satisfy safety and stabilization constraints in practical applications, and a common control that satisfies the safety and stabilization objectives may not exist since both objectives may be in conflict[13–15].

To simultaneously achieve safety and stabilization constraints of nonlinear systems, several control design approaches have been established based on the merging of(control)Lyapunov functions and(control)barrier functions[16–18],where the(control)Lyapunov functions guarantee stabilization while the(control)barrier functions guarantee safety of the state trajectories[14,19].Particularly,to handle conflicting safety and stabilization objectives,unification of(control)Lyapunov functions and(control)barrier functions conditions into a quadratic program (QP) has been studied in [6,11], which allows compromising the (control) Lyapunov functions-defined control objectives to enforce safety.However, despite the appealing idea in the aforementioned literature for guaranteeing safety and stabilization,it remains unclear on how to deal with conflicting safety and stabilization objectives for switched systems.

Duetotheirtheoreticalandpracticalsignificance,switched systems have gained much attention for the last decades[20–22].Also,different properties of switched systems,such as stability and stabilization criteria, have been proposed in[23–25]. However, in practical situations, besides stability and stabilization performance,safety may also be crucial for switched systems. Recently, in [26–29], some safety verification approaches have been successfully applied to the analysis and design for switched systems. However, to the best of our knowledge, no results about safety stabilization in switched systems have been reported.Moreover,when no safety and stabilization problem for all subsystems is solvable,how to solve the safety stabilization problem via design of a proper switching law? Obviously, the classical control design approaches in the aforementioned literature cannot be directly applied,and new design tools are required.

It is worth pointing out that in[6,11],when conflict occurs,safety is strictly guaranteed while convergence to goal is relaxed based on a (control) Lyapunov function relaxation factor.Then comes a question:can a more general condition than relaxing the stabilization term in [6,11] be provided?For example,each subsystem has only stabilization in some subregion of the state space,can we still achieve stabilization with guaranteed safety?For the existing results in[6,11,26–29],the answer is negative.However,in the switched systems framework,it might be possible to achieve safety stabilization by appropriate switching.

Motivated by the aforementioned discussions,the objective of this paper is to develop sufficient conditions for the safety stabilization problem of switched systems by design of a state-dependent switching strategy with guaranteed dwelltime. Compared with the existing results on switched and non-switched systems,the contribution of this paper is twofolds.First of all,a sufficient condition is given to verify the problem of safety stabilization for switched systems for the first time.Also,to simultaneously guarantee the safety of the switched system and stabilize the system,a novel switched control design method is proposed by exploiting the union of a common barrier function and a single Lyapunov function, which effectively handles the conflict between safety and stability objectives. Second, in order to effectively utilize the stabilization with a guaranteed safety property in a subregion for each subsystem, a novel state-dependent switching law is designed without the help of predesigned dwell-time requirements to obey a positive dwell-time constraint[30,31],and a sufficient condition to avoid the Zeno behavior is derived. Also, a solvability condition for safety stabilization of switched systems is derived by exploiting the union of a common barrier function and a common Lyapunov function.

Notations The interval[0,∞)in the space of real numbers R is denoted by R+.For a given bounded setD⊆Rn,the distance of a pointξ∈Rnwith respect toDis defined as|ξ|D=infa∈D‖ξ-a‖,where‖·‖denotes a metric norm.A functionα: R+→R+is of classKif it is continuous,strictly increasing,andα(0)= 0,and it is of classK∞if in additionα(s)→∞ass→∞.A functionβ:R+×R+→R+is of classKKifβ(·,t)is of classKfor each fixedt≥0,and similarly,β(s,·)is of classKfor each fixeds≥0. A functionβ: R+×R+→R+is of classKLifβ(·,t)is of classKfor each fixedt≥0, andβ(r,t)decreases to 0 ast→∞for each fixedr≥0. (see [21] for details). A functionφ(x)is said to be positive definite ifφ(0)=0 andφ(x)＞0 for anyx/=0 ∈Rn.

2 Problem formulations and preliminaries

Consider a family of switched systems of the form

wheret0is the initial time,x0is the initial state,Ndenotes the set of nonnegative integers.Whent∈[t j,t j+1),σ=k j,that is,thek j-th subsystem is active.Also,we assumek j/=k j+1for allj(see[20,22]for details).

The switching signalσis said to be withdwell-time τ,ift j+1-t j≥τfor any two consecutive switching timest jandt j+1.

Denote byx(t)the trajectory or solution of the switched system(1)at timet≥t0,starting atx0att=t0.In addition,the solutionx(t)of the switched system (1) is assumed to exist and to be unique. It is assumed that the state of the switched system(1)does not jump at the switching instants.

LetD⊂Rnbe the set of unsafe states,which is assumed to be known,and 0/∈D.In general,the set of unsafe statesDis defined by physical constraints or safety requirements.

We will discuss the following problem in this paper.

Problem 1 (Safety stabilization problem) For the switched system (1) with a given set of unsafe statesD, design a switching lawσ, such that for allx0∈RnDand for allt≥t0, the switched system (1) is safe and asymptotically stable, i.e.,x(t)/∈Dand the switched system (1) is stable and limt→∞x(t)=0.

Our main objective is to solve the safety stabilization problem for the switched system (1) by design of a statedependent switching strategy with a guaranteed dwell-time.In this paper,the solvability of the safety stabilization problem for subsystems is not assumed.This is because if there exists a subsystem in the switched system(1)for which the safety stabilization problem is solvable,then the safety stabilization problem of(1)is trivial.

In Assumption 1,the inequalities(3a)and(3b)are commonly used conditions in [14,19,32]. The inequality (3c)implies that all subsystems of the switched system(1)admit a common barrier functionB(x).The solvability of inequality(3d)is weaker than the standard partial differential inequalities in [32] since the inequality (3d) is only satisfied in a subregionΩkof the whole state space Rn.Also,in order to guarantee a positive dwell-time between consecutive switchings, we needV(x)andφ(x)to satisfy the properties (3d)and(3f).

3 Main results

In this section, we discuss how to design a proper statedependent switching strategy with guaranteed dwell-time in order to achieve the safety stabilization problem for the switched system(1).

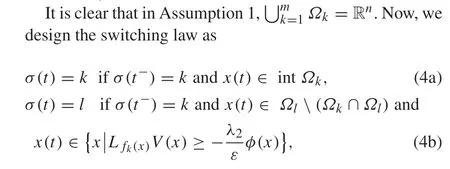
whereε ＞1 is a constant,andσ(t0)=kwithx0∈ΩkD.

Remark 1Obviously, by the switching law (4), whenx(t)is in the interior ofΩk, the value ofσ(t)=kremains unchanged;whenx(t)entersΩk∩Ωl,the value ofσ(t)=k

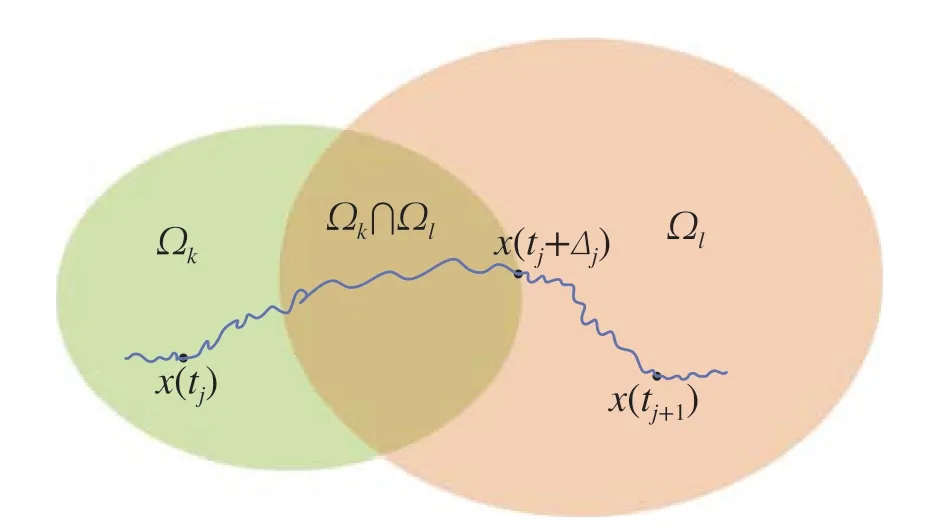
Fig.1 Diagram of the switching law(4)

Theorem 1Suppose that the switched system(1)with a given unsafe set D⊂Rn satisfies Assumption 1. Then the safety stabilization problem for(1)is solvable, and no executions are Zeno under the switching law(4).

ProofThe proof consists of two parts. The first part is to prove the stabilization with guaranteed safety of the switched system(1).The second part is to prove the nonexistence of Zeno executions.

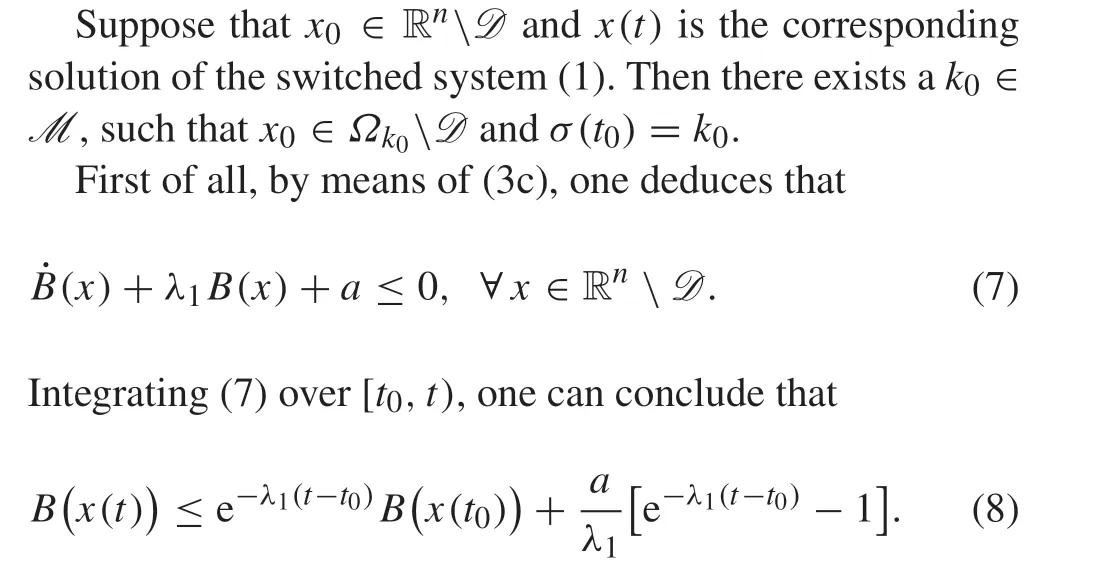
Hence,the switched system(1)under the switching law(4)is stable in the sense of Lyapunov.Moreover,since the inequality in(3d)holds strictly forx/= 0,the asymptotic stability follows from the standard argument of Lyapunov theory.

Next,we show that no executions of the switched system(1)are Zeno,i.e.,there exists a positive dwell-time between any two consecutive switching instantst jandt j+1,j∈N.

According to(3d),(3e),(3f),the switching sequence(2),the switching law(4)and Remark 1,one gets

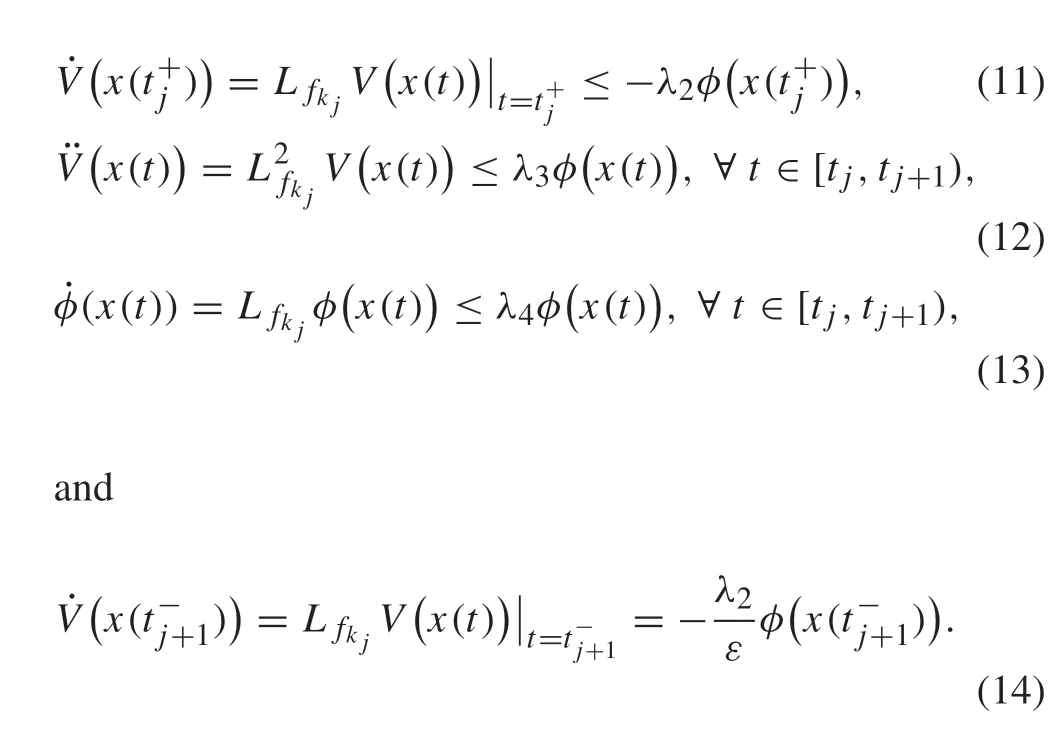
In this paper,we defineC1functionB(x)satisfying(3a)and(3c),as a common barrier function.Also,we defineC1functionV(x)satisfying(3b)and(3d),as a single Lyapunov function.

Remark 2It is important to note that in Theorem 1,the existence of a common barrier function and a single Lyapunov function implies that the switched system (1) is asymptotically stable, while avoiding an unsafe setD, i.e., the trajectoryx(t)of the switched system (1) which starts in RnDwill not enterDunder the switching law designed(4).

Remark 3In the state-dependent switching strategies considered, a common restriction in which a finite number of switches occur on every bounded time interval is needed to rule out Zeno behavior[20,21,25,33].However,the designed state-dependent switching strategies in [20,21,25,33] do not guarantee a minimal dwell-time between consecutive switchings.The practical case is one where a minimal dwelltime between consecutive switchings is required [21,22].Recently, [30,31] have provided state-dependent switching laws to obey a dwell-time constraint,but a set of predesigned dwell-time requirements is required.It should be pointed out that,in this paper,the switching law(4)is designed without the help of predesigned dwell-time requirements to obey a positive dwell-time constraint,and a novel switched control design framework is developed to strictly ensure simultaneous stabilization and safety enforcement of the switched system(1).

Remark 4Theorem1simultaneouslyguaranteesthesafetyof the switched system and stabilizes the system based on the union of a common barrier function and a single Lyapunov function, which may provide an unified view of the barrier function and Lyapunov function theories and effectively handles the conflict between safety and stability objectives. In fact,in this paper,each subsystem does not necessarily have the safety stabilization property in the whole state space,but it has the safety stabilization property in some subregions of the state space.In fact,how to simultaneously satisfy barrier and Lyapunov function conditions are important in practice and but technically challenging.

In what follows, we give a convex combination-based method for finding such a single Lyapunov functionV(x).

LetV(x): Rn→R andφ(x): Rn→R beC1positive definite functions,andλ2＞0 be a constant.

Then the safety stabilization problem for the switched system(1)is solvable under arbitrary switchings.

Remark 5It should be also mentioned that recently, for switched systems, sufficient conditions for safety verification have been derived in [26–29]. However, those results mentioned above cannot be directly applied to verify safety stabilization in switched systems.In Corollary 1,a sufficient condition for safety stabilization of switched nonlinear systems is obtained for the first time.

4 Two illustrative examples

In this section, to verify the effectiveness of the approach proposed,two examples are considered.

Example 1Consider a simple mobile robot navigation described by

with a given unsafe setD= {x∈R2|x1＞2},wherex=[x1,x2]Tis the position, andv= [v1,v2]Tis the velocity

The simulation result is depicted in Fig.2 with the initial conditionx0= [-2.2,1]T. It can be seen from Fig.2 that the state trajectories converge to zero,and the lower-bound of|x(t)|Dis larger than 0,which implies that the state trajectory of the system(23)avoids the set of unsafe stateD,i.e.,the switched system(23)is safe and stable under the switching law shown in Fig.2.

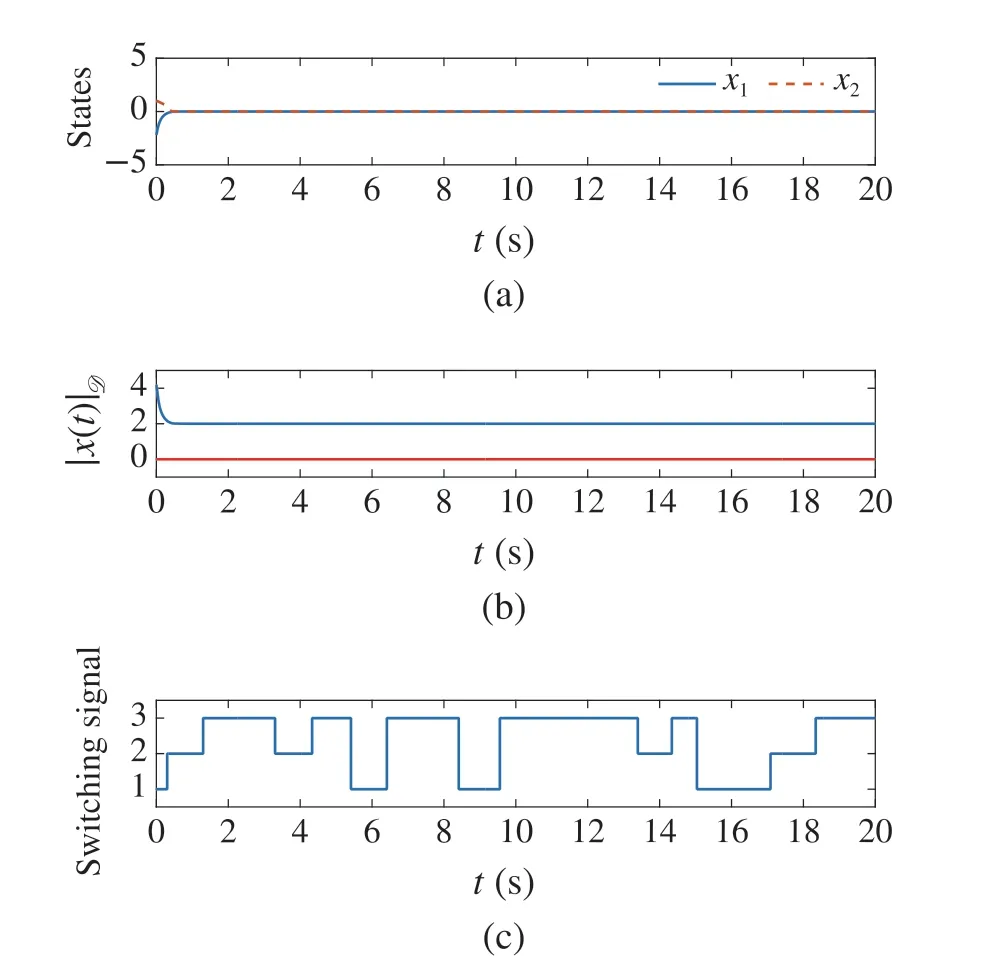
Fig. 2 Trajectories of x(t) = [x1(t),x2(t)]T, |x(t)|D, and σ(t) in Example 1

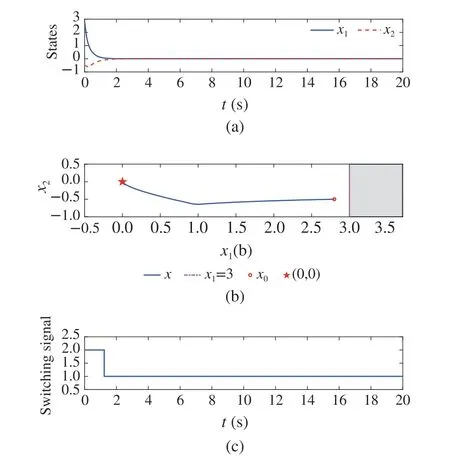
Fig.3 State trajectories,σ(t),and the set of unsafe state D is shown in grey area in Example 2

5 Conclusions

In this paper,a novel switched control design framework has been developed to strictly ensure simultaneous stabilization and safety enforcement of switched systems based on the union of a common barrier function and a single Lyapunov function. Also, the solvability of the safety stabilization problem for individual subsystems has been unnecessary.A state-dependent switching strategy with guaranteed dwelltime for switched systems has been designed,and sufficient condition for absence of Zeno behavior has been derived.