Learning-based adaptive optimal output regulation of linear and nonlinear systems:an overview

Weinan Gao·Zhong-Ping Jiang

Abstract This paper reviews recent developments in learning-based adaptive optimal output regulation that aims to solve the problem of adaptive and optimal asymptotic tracking with disturbance rejection.The proposed framework aims to bring together two separate topics—output regulation and adaptive dynamic programming—that have been under extensive investigation due to their broad applications in modern control engineering. Under this framework, one can solve optimal output regulation problems of linear, partially linear, nonlinear, and multi-agent systems in a data-driven manner. We will also review some practical applications based on this framework,such as semi-autonomous vehicles,connected and autonomous vehicles,and nonlinear oscillators.

Keywords Adaptive optimal output regulation·Adaptive dynamic programming·Reinforcement learning·Learning-based control

1 Introduction

1.1 Background

The output regulation problems [1–11] concern designing controllers to achieve asymptotic tracking with disturbance rejection for dynamic systems,wherein both disturbance and reference signals are generated by a class of autonomous systems, named exosystems. It is a general mathematical formulation applicable to numerous control problems arising from engineering,biology,and other disciplines.

The evolution of output regulation theory can be summarized by three phases. In the first phase, the theory of servomechanism was actively developed to tackle output regulation problems based on classical control theory in the frequency domain tracing back to the 1940s [12,13]. After the state-space representation was introduced by Kalman,pioneers in the automatic control community, including Davison, Francis, and Wonham, have extensively studied the linear output regulation problem with multiple inputs and multiple outputs [5,14–17]. With some mild assumptions on the exosystem and plant,the solvability of the linear output regulation problem is reduced to the solvability of a class of Sylvester equations, called regulator equations.There are two major strategies for addressing output regulation problems: feedback-feedforward and internal model principle [16]. By means of the internal model principle,one can convert an output regulation problem to a stabilization problem of an augmented system composed of the plant and a dynamic compensator named internal model.Another remarkable feature of the internal-model based control schemes is that they guarantee asymptotic decay of the tracking error while tolerating plant parameter uncertainties.Asanextensionofthetraditionalinternalmodelprinciple,the notion of adaptive internal model was proposed by taking the totally unknown exosystem into consideration [18]. Moreover, the cooperative output regulation problems of linear multi-agent systems[19–24]have drawn considerable attention over the last decade which include the leader-follower consensus as a special case.

In the second phase,the control community has turned its attention to the development of a theory for nonlinear output regulation due to the fact that almost all the real-world control systems are nonlinear, and many of them are strongly nonlinear.The nonlinear output regulation problem was initially studied for the special case when the exosignals are constant[25]. Owing to the pioneering work of Isidori and Byrnes[7], the solvability of nonlinear output regulation problem was linked to that of a set of nonlinear partial differential equations,named nonlinear regulator equations.The solution to the nonlinear regulator equation contributes to a feasible feedforward control input. By center manifold theory [26],one can design a corresponding feedback-feedforward control policy to achieve the nonlinear output regulation.Since nonlinear regulator equations contain a set of partial differential equations,it cannot be ignored that to obtain the analytic solution to these equations is generally hard.With the above obstacle in mind,Huang and Rugh offered an approximated solution of the nonlinear regulator equation by power series approaches [27].Similar to linear output regulation, (adaptive)internal model based solutions have also been proposed for nonlinear output regulation problems; see [28–32] and references therein.To realize asymptotic tracking and disturbance rejection in an optimal sense is another major task in outputregulationtheory;see[33–35].Toourbestknowledge,Krener firstly opened the door of nonlinear optimal output regulation[34].His solution starts from solving the nonlinear regulator equation,then a feedback controller is obtained by solving the Hamilton–Jacobi–Bellman equation.The asymptotic convergence of the tracking error can be ensured by LaSalle’s invariance principle.

Notice that most solutions developed in the first and second phases are model-based. Owing to the fact that developing mathematical models for physical systems is often costly,time-consuming,and involves uncertainties,the third phase is devoted to the integration of data-driven and learning-based techniques for output regulator design.This phase shift is strongly motivated by the exciting developments in data science,artificial intelligence(AI)and machine learning that have received tremendous media coverage over the last few years. For instance, deep neural networks and reinforcement learning techniques have been bridged such that the agent can learn efficiently towards the optimal control policy despite of its uncertain and complex environment[36,37].Inspired by the deep reinforcement learning theory,the Google DeepMind team has invented its own AI players of Go game,named AlphaGo and AlphaGo Zero,which have shown their superiority against human players[38,39].In the area of output regulation,neural network based approaches have been proposed in [40,41] to approximate the solution to nonlinear regulator equations.A numerical method based on successive approximation, which is an important tool in machine learning, has been proposed to obtain the center manifolds and to solve the nonlinear output regulation problem [42]. Nevertheless, it is a longstanding challenge to generalize existing solutions to tackle the learning-based adaptive optimal output regulation problem, which aims at realizing output regulation and optimizing the closed-loop system performance under unknown system model.The purpose of this paper is to provide an overview of our recent works,see,e.g.,[43–45],on the learning-based output regulation,that are aimed at learning adaptive and optimal output regulators from input and state or output data collected along the trajectories of the control system.

1.2 Learning-based adaptive optimal output regulation

The framework of learning-based adaptive optimal output regulation is depicted in Fig.1. Based on this framework,the optimal controller that achieves output regulation can be learned through the actor-critic structure, which is popular in adaptive dynamic programming (ADP) [46–68]. As an important branch of reinforcement learning, ADP concentrates on how an agent should modify its actions to better interact with an unknown environment to achieve a longterm goal. It is thus a good candidate to solve adaptive optimal control.Existing ADP methods include policy iteration (PI) [50,51,53,55,61,62,69] and value iteration (VI)[46,52,60,70–72].

There are several reasons why we have developed the learning-based adaptive optimal output regulation framework.

1. Fundamentally different from most existing output regulation approaches,the developed learning-based adaptive optimal output regulation framework does not rely on either the knowledge of system model or the system identification. It is a non-model-based and direct adaptive control framework.

2. Practically,non-vanishing disturbance,time-varying references,and dynamic uncertainties may exist simultaneously in many control systems; see, e.g., [73]. Unfortunately,existing ADP approaches often do not consider the challenge to tracking control arising from the co-existence of these factors. The proposed framework successfully fills in this gap,and thus it significantly enhances the practicability of ADP.

3. The developed framework has a wide applicability. One canleverageittotackleadaptiveoptimaloutputregulation problems of linear,partially linear,nonlinear,and multiagent systems.

Fig.1 The framework of learning-based adaptive optimal output regulation

The remainder of this papar is organized as follows. In Sect.2,we present two learning-based solutions to the adaptive optimal output regulation problem of linear systems:feedback-feedforward and internal model principle.In Sect.3, we have achieved learning-based robust optimal output regulation of partially linear composite systems via robust ADP [53]. To solve the learning-based output regulation problems of multi-player systems,a solution based on ADP and game theories is given in Sect. 4. Sections 5 and 6 target on the learning-based cooperative output regulation problems,while Sect.7 contains the learning-based adaptive optimal output regulation of nonlinear systems.Application results are discussed in Sect.8,while Sect.9 concludes this overview paper by a summary and overlook.

2 Learning-based adaptive optimal output regulation of linear systems

We begin with a class of continuous-time linear systems described by

where the vectorx∈Rnis the state,u∈Rmis the control input,andv∈Rqstands for the exostate of an autonomous system(2),named the exosystem .A∈Rn×n,B∈Rn×m,C∈Rr×n,D∈Rr×m,E∈Rn×q,F∈Rr×qandS∈Rq×qare system matrices.d=Evrepresents the external disturbance,y=Cx+Duthe system output,yd= -Fvthe reference signal,ande∈Rrthe tracking error.

Throughout this paper,we make the following assumption on the exosystem.

Assumption 1 The origin of exosystem(2)is Lyapunov stable,and all the eigenvalues ofShave zero real parts.

2.1 Adaptive optimal feedback-feedforward controller design

With respect to the system (1)–(3), the linear output regulation problem has been solved through the feedbackfeedforward control strategy [5], i.e., to design a controller in the form of

such that the closed-loop system is globally exponentially stable and the tracking error asymptotically converges to zero, whereK∈Rm×nandL∈Rm×qare feedback and feedforward control gains,respectively.

Beyond the linear output regulation problem, the linear optimal output regulation problem has been proposed in[34]considering both asymptotic tracking and transient performances of the closed-loop control system.Specifically,with the complete knowledge of system dynamics,one can design a controller as follows to solve the linear optimal output regulation problem

whereK*is the optimal feedback control gain which can be obtained by solving the dynamic optimization Problem 2,and the corresponding feedforward control gainL*isL*=U*+K*X*.The pair(X*,U*)is the minimizer of Problem 1.Now we ready to formulate these Problems 1 and 2.

Problem 1

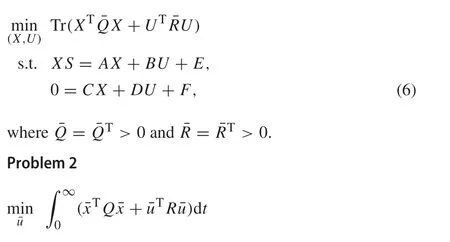
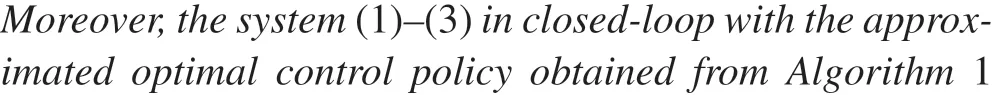
Algorithm1(ADPlearningalgorithmforsolvinglinearoptimal output regulation problems)1: Compute basis matrices X0,X1,··· ,Xh+1.2: Utilize u =-K0x+ξ on[t0,ts]with bounded exploration noise ξ and a stabilizing K0.3: Select a small ∈＞0.i ←0, j ←0 4: repeat 5:Solve Pj,K j+1 from(9)6:j ←j +1 7: until|Pj - Pj-1|≤∈8: j* ←j,i ←i +1 9: repeat 10:Solve S(Xi)from(9)11: until i =h+1 12: Find(X*,U*)

Note that the presented method is generalizable to the cases of discrete-time linear systems with time delay. We refer the interested reader to recent papers[74,75].

2.2 Adaptive optimal controller design based on internal model principle

Besides feedback-feedforward control methods, the second class of solutions to output regulation problems rely on the internalmodelprinciple[16].Thesolutioncomesfromdeveloping a dynamic feedback controller

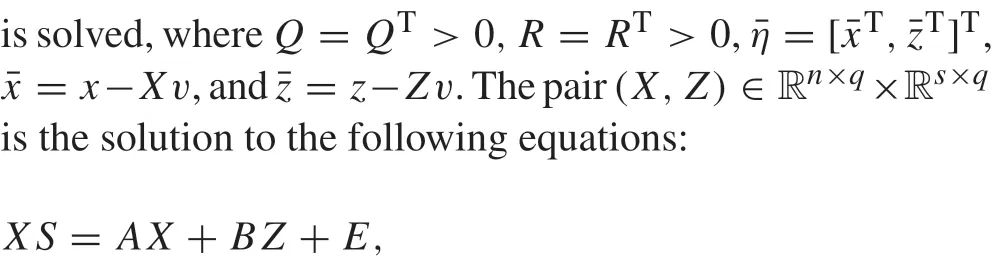
3 Learning-based robust optimal output regulation of partially linear composite systems

The purpose of this section is to show that the Theorem 1 can be generalized to solve the robust optimal output regulation problem of a class of partially linear composite systems[77].The system in this class is an interconnection of a linear subsystem and a nonlinear subsystem named the dynamic uncertainty,which is modeled as follows:

holds,then the robust optimal output regulation problem of the partially linear composite system(13)–(16)is solvable by the robust optimal controller u=-K*(x-X*v)+U*v.

Even if the system dynamicsA,B,E,g,Δare unknown withζunmeasurable,the control gain of the robust optimal controller,K*,X*,U*,can be learned online following the Algorithm 1 withureplaced byu+Δ.Please refer to[80]for mode details.

4 Game and learning-based output regulation for multi-player systems

There is only one player in all the system models considered in previous sections.In this section,we study the non-zerosum game output regulation problem for continuous-time multi-player linear systems. Our goal is to learn the Nash equilibrium through online data collected along the system trajectories.The linear continuous-time systems with multiple players are described by

Remark 1Note that it is usually difficult to solve (31) analytically as it is a system of coupled nonlinear functions.Interestingly, one can leverage the data-driven ADP algorithm proposed in [83] to numerically approximate the solution to (31) and the corresponding feedback and feedforward control gains via online data.

The following theorem discusses the convergence of the ADP algorithm and the tracking ability of the closed-loop system.

As an extension,we have recently solved the global robust optimal output regulation problem of partially linear composite systems with both static and dynamic uncertainties in[84].In order to overcome this challenge,we have combined game theory,small-gain theory[85],output regulation theory and ADP techniques.

5 Learning-based cooperative optimal output regulation of multi-agent systems

In this section,we will present data-driven distributed control methods to solve the cooperative optimal output regulation problem of leader-follower multi-agent systems. Different from existing work, a distributed adaptive internal model is originally developed which is composed of a distributed internal model and a distributed observer to mimic the leader’s dynamics and behavior.

Consider a class of linear multi-agent systems

Note that the cooperative output regulation problem is solved if one designs a control policy such that the closedloop multi-agent systems are asymptotically stable (in the absence ofv) and limt→∞ei(t)= 0,fori= 1,2,...,N.We show in the Lemma 1 that the cooperative output regulation problem is solvable by developing a distributed adaptive internal model.

is Hurwitz for all the followers. Based on Lemma 1, the designed optimal controller (52) can be used to solve the cooperative optimal output regulation problem.

Note that PI and VI are two typical ADP methods to deal with adaptive optimal control problems.We will concentrate on designing data-driven adaptive optimal control policies based on PI and VI, and solving the cooperative optimal output regulation problem in a model-free sense.

To begin with, it is brought to attention that the leader’s state information is required by all followers. Although we cannot measure this information directly from the multiagent systems,we can develop an estimator of leader’s statev.

whereμ2＞0.

5.1 Online PI design

To begin with, we rewrite the augmented system (34)–(38)by

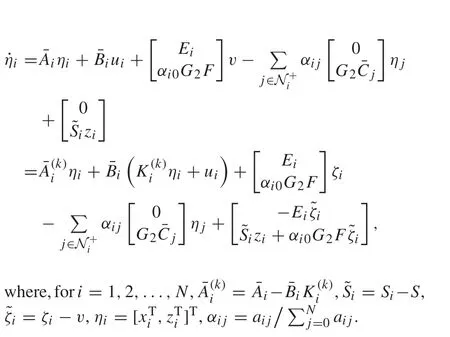
5.2 Online VI design

Essentially, the VI algorithm is to update the value matrix and control gain by

It is interesting to note that the proposed research can be extended to the case of cooperative optimal output regulation of discrete-time multi-agent systems [87], and cooperative adaptive optimal control of continuous-time multi-agent systems with ensured leader-to-formation(LFS)stability[45],which indicates how the leader inputs and disturbances affect the stability of the formation.

6 Learning-based cooperative robust optimal output regulation of partially linear multi-agent systems

The solution presented in the previous section does not take the dynamic uncertainty into consideration. In this section,we aim at solving the cooperative robust optimal output regulation of multi-agent system in the presence of dynamic uncertainties.

To begin with, consider a class of heterogeneous and multi-agent systems

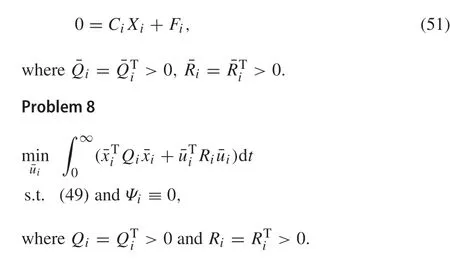
By linear optimal control theory and output regulation theory,the decentralized optimal controller can be designed through solving AREs.However,this controller is designed under two strong conditions:(1)Ψi≡0,(2)each agent can directly communicate with the exosystem.We will present an approach based on cyclic-small-gain theory and robust adaptive dynamic programming which can remove the Condition(1),and relax the Condition(2)by the Assumption 6.To be more specific,under the Assumption 6,the robust distributed controller is developed as follows:

Then, the system(49)in closed-loop with(52)–(53)achieves cooperative output regulation.

One can leverage the robust ADP algorithm in[88]to learn the control gainsK*iandL*i.The convergence has also been rigorously analyzed therein.

7 Learning-based adaptive optimal output regulation of nonlinear systems

In this section, we focus on the adaptive optimal output regulation problem of continuous-time nonlinear systems.Consider the class of strict-feedback nonlinear systems described by

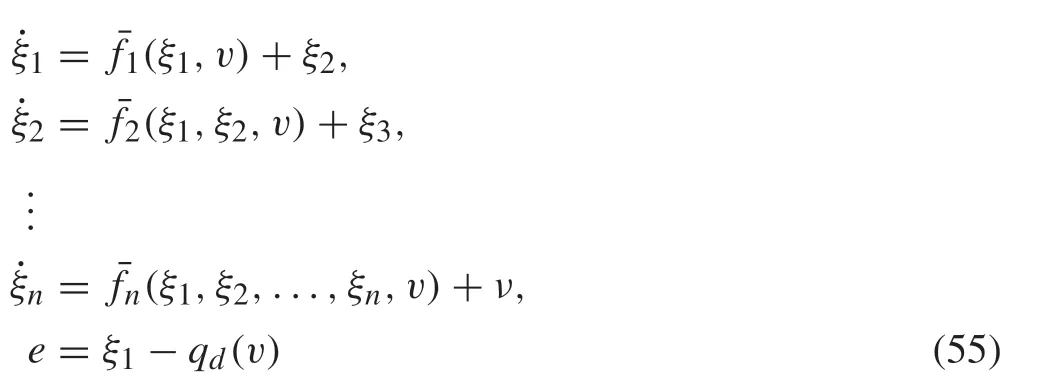
whereQ: Rn→R is positive definite and proper, andris a positive constant with initial conditionsx0=x(0)andv0=v(0).

Lettingξ(v)=[ξ1(v),...,ξn(v)]T,the nonlinear optimal output regulation problem is formulated as follows:

Then,we present a model-based PI method starting from an admissibleu1:

7.1 Phase-one learning:solving regulator equations

7.2 Phase-two learning:solving HJB equations

Theorem 6 [44]Consider the nonlinear plant (55), the exosystem (2) in closed-loop with the approximate optimal controller obtained by[44,Algorithm 2]Then,the following properties hold:

(1)The trajectory of the closed-loop system is bounded for any t≥0.

(2)The tracking error e(t)is uniformly ultimately bounded with arbitrarily small ultimate bound.

Notice that the results in this section has been generalized to solve cooperative optimal output regulation problem of nonlinear discrete-time systems in[91].

8 Applications

The aim of this section is to demonstrate the broad applicability and efficiency of the developed learning-based adaptive optimal output regulation approaches. Through using semi-autonomous vehicles as an example, we validate the learning-based adaptive optimal output regulation approach.We further apply the learning-based cooperative output regulation approaches on connected and autonomous vehicles.Last but not least,we leverage learning-based nonlinear output regulation approaches on Van Der Pol Oscillators.

8.1 Application to semi-autonomous vehicles

In this section,we present a data-driven shared control framework of the driver and the semi-autonomous vehicle to obtain the desired steering control performance. The terminology semi-autonomous refers to the situation that an auxiliary copilot controller and the human driver manipulate the vehicle simultaneously.By leveraging the small-gain theory,we have developed shared steering controllers which is not relied on the unmeasurable internal states of human driver. Furthermore, by adopting data-driven ADP and an iterative learning scheme, the shared steering controller is learned from real-time data collected along the trajectories of the interconnected human-vehicle system.

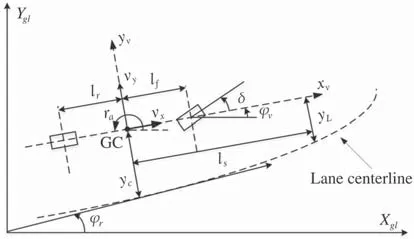
Fig.2 Vehicle model illustration

The vehicle model for steering control is described by

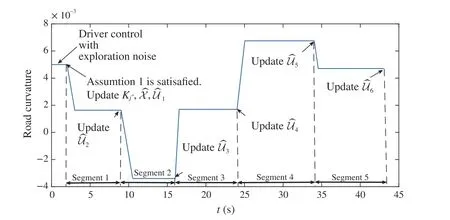
Fig.3 Road curvature profile

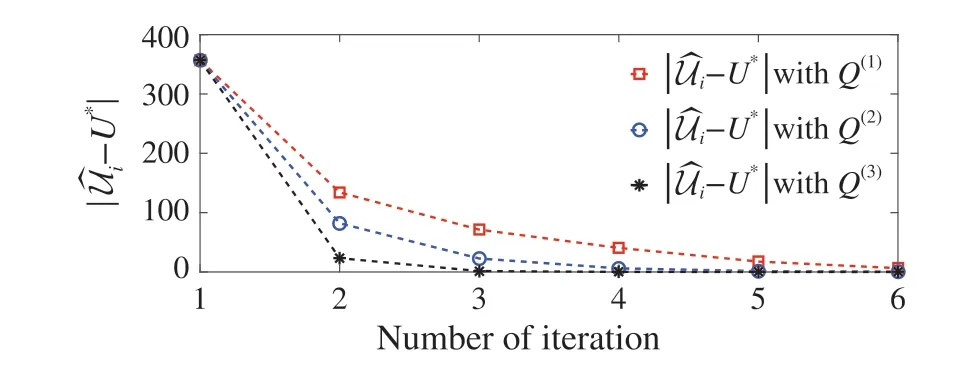
Fig. 4 Convergee of Ui during drivi with different chosen Q values

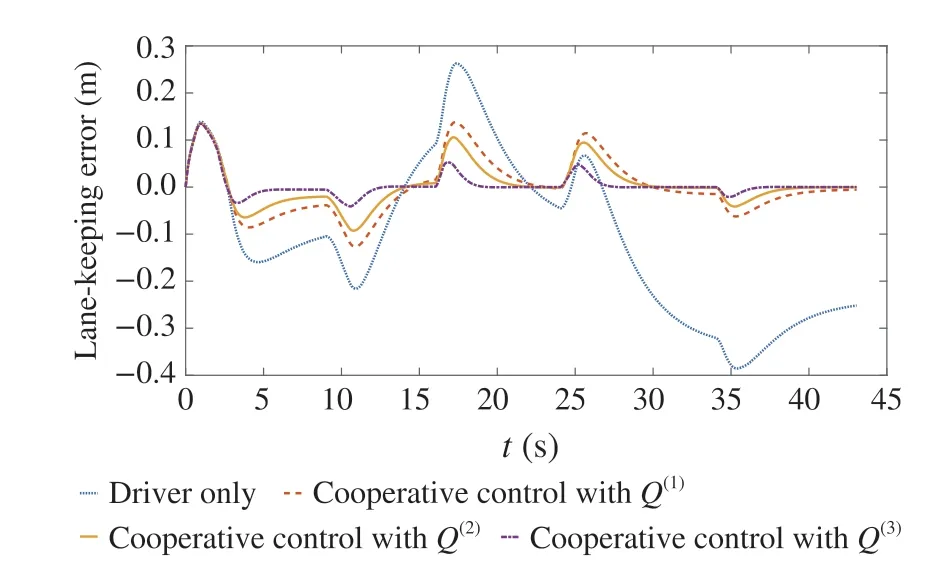
Fig. 5 Lane-keeping performance comparison between driver and shared control strategies with different Q values

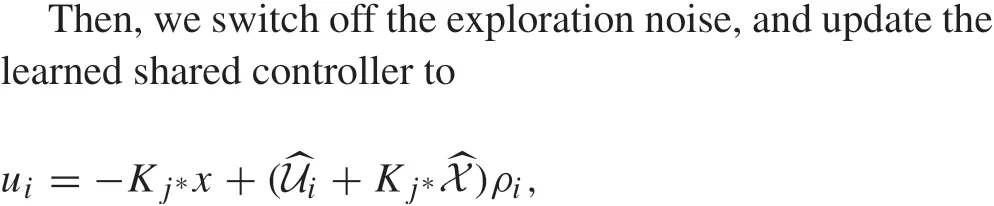
8.2 Application to connected and autonomous vehicles

whereuirepresents the desired acceleration of vehiclei.Forj=i-1,i,xk= [Δhk,Δvk,ak]Tincludes the headway and velocity errors,and the acceleration of vehiclek.

Fig.6 Buses in closed-loop with data-driven CACC controller,a traffic simulation via Paramics

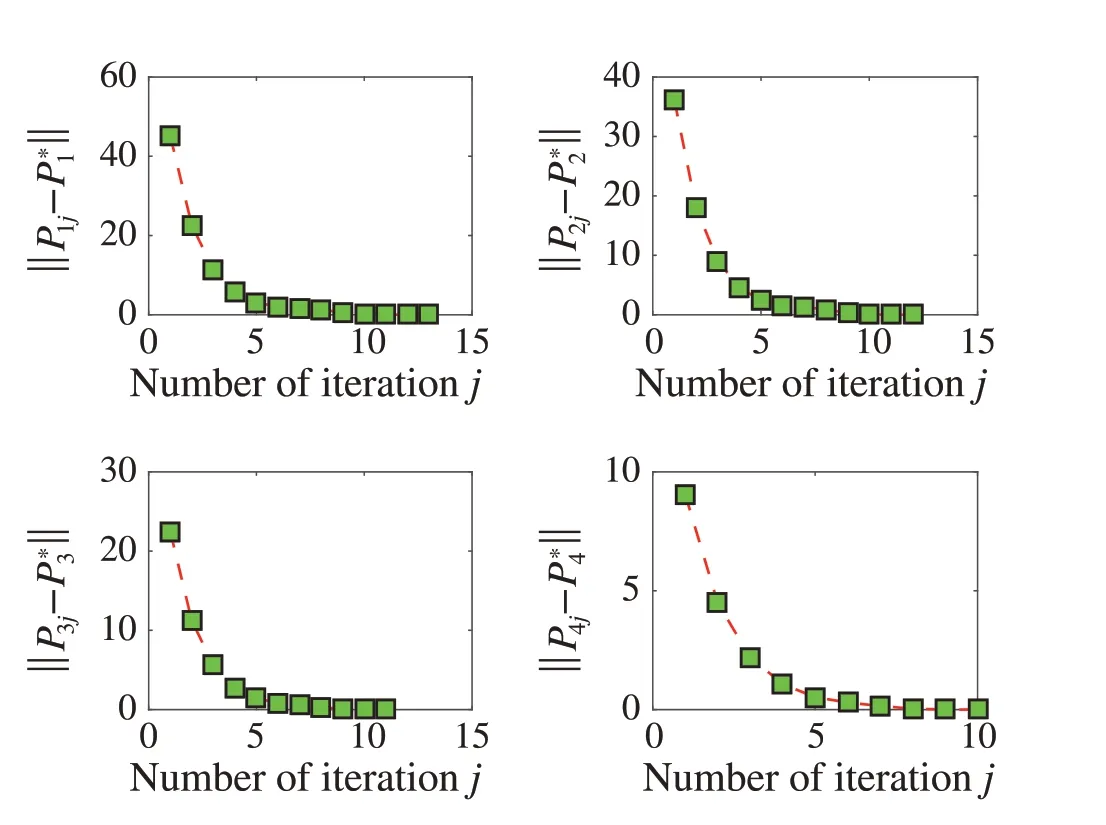
Fig. 7 The comparison of learned value matrix Pi j and the optimal value matrix P*i

Remark 2Another scenario is considered in [96] where a platoon ofnhuman-driven vehicles is followed by an autonomous vehicle. A data-driven connected cruise control has been designed therein.We have further included the vehicle-to-infrastructure (V2I) communication and developed data-driven predictive cruise control approaches in[97,98].

The ADP algorithm to learn theK*iandP*ihas been proposed in [94] and validated by the Paramics micro-traffic simulation.

Figure6 shows buses(with green shape)by using the datadriven control algorithm in the traffic simulations. These buses operate with roughly the same headway. We have selectedaplatoonof 4autonomous buses ontheexclusivebus lane to observe the convergence.The learned valuePi jand corresponding optimal valueP*iof theith bus are compared in Fig.7.The the comparison of learned control gain and the optimal gain is shown in Fig.8. It shows that the learning stops at less than 15 iterations for all the autonomous buses.

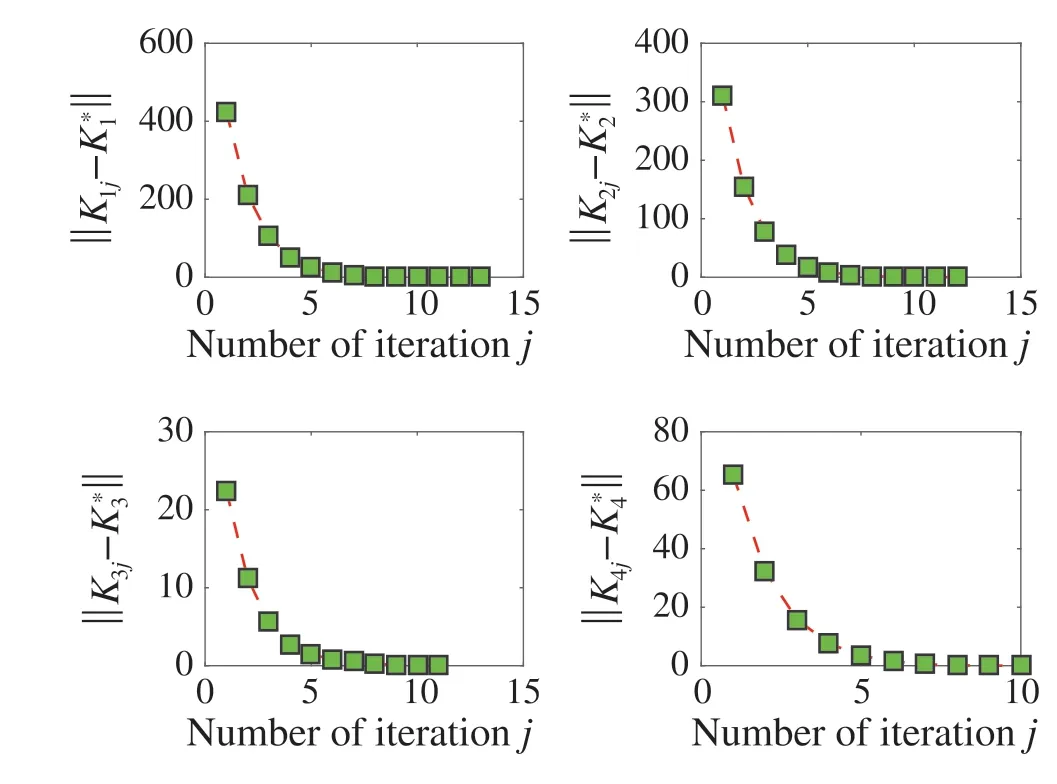
Fig. 8 The comparison of learned value matrix Ki j and the optimal value matrix K*i

8.3 Application to Van Der Pol oscillators

Consider a nonlinear Van der Pol oscillator modeled by

where the system parameterιis unknown but within the range of [-0.3,-0.5]. The exosystem (2) is a marginally stable autonomous system modeled by

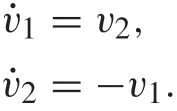
In order to validate the effectiveness of the nonlinear adaptive optimal output regulation techniques, we have applied the[44,Algorithms 1 and 2]to approximate the optimal controller via collected input and state data from the oscillator.

In order to generate online data, we setι= -0.5 and initial values of(exo)states byξ(0)= [2,-4]Tandv(0)=[0,0.5]T.Initially,the control inputμ(t)is a summation of sinusoidal noises with different frequencies in order to excite the system,which is function obtained by the first iterationV1(x,v)in Figs.11 and 12.It is checkable that the cost of the closed-loop system reduce dramatically after the online learning.

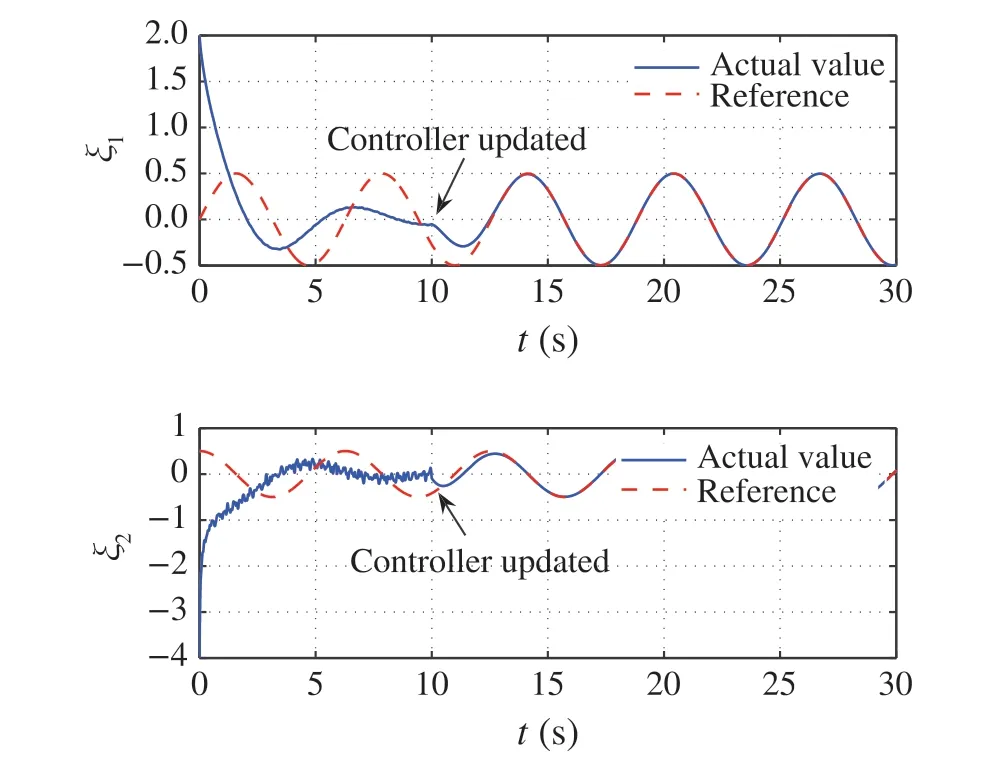
Fig.9 System state and reference trajectories

Fig.10 Evolution of weights of value function and control policy

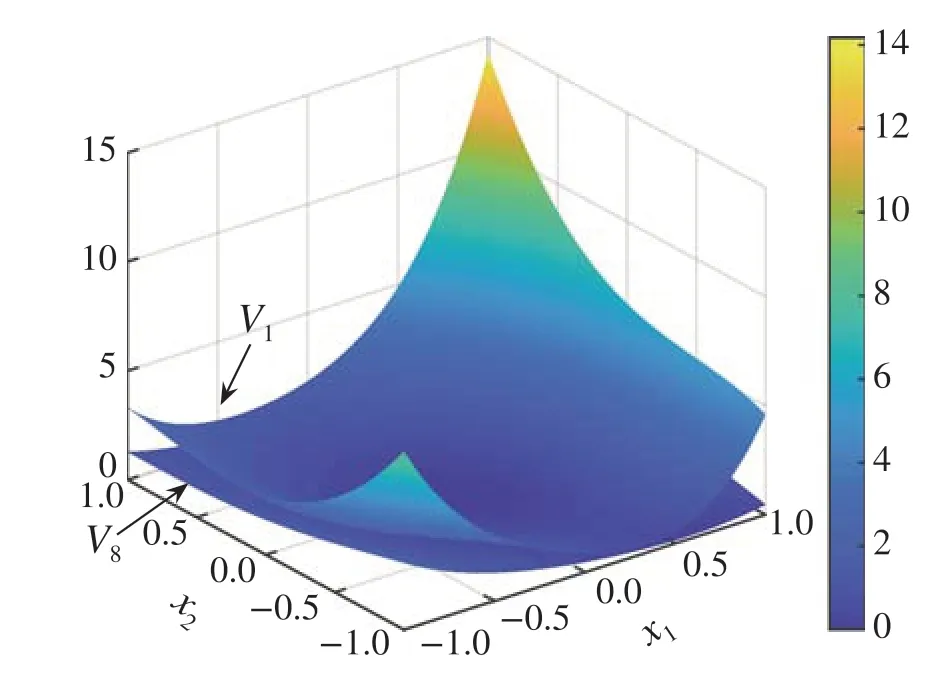
Fig. 11 System costs with different control policies under v1 = 0.5 and v2 =0

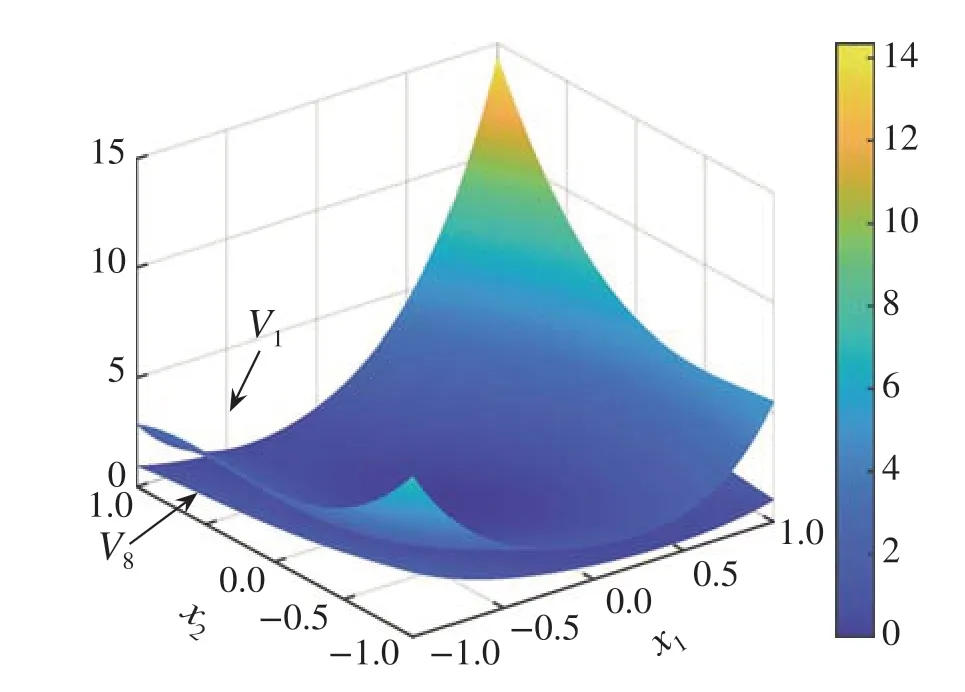
Fig.12 System costs with different control policies under v1 = v2 =0.3536

9 Summary and outlook

This paper is an overview of the recent progresses in output regulation and ADP,including our work in learningbased adaptive optimal output regulation. The proposed learning-based framework is different from traditional output regulation approaches that are mostly model-based. It also enhances the practicability of ADP as it considers nonvanishing disturbance,time-varying reference,and dynamic uncertainties in the control system together.We have shown in this overview that the framework can be used to solve the adaptive optimal output regulation of dynamic systems in different models,which attests its wide applicability.

Future research directions under the proposed frameworkincludelearning-basedrobustoptimaloutputregulation of nonlinear systems with dynamic uncertainties, learningbased stochastic adaptive optimal output regulation with unmeasurablenoises,andlearning-basedresilientoutputregulation under malicious cyberattacks.