基于标签映射的长短期浏览行为数据挖掘仿真

陈 清，张 程，刘 瑛

(华东交通大学理工学院，江西 南昌 330100)

1 引言

随着信息技术的快速发展，给用户带来大量多标签数据的同时，随之也增加了对数据信息处理的难度[1]。数据分类是数据挖掘中处理信息的有效途径，大部分数据均属于高维数据，并且在高维空间存在的状态是十分稀疏的，对这些高维数据进行处理、计算与分析是尤其重要的，传统的数据挖掘形式仅考虑数据的几何结构，易忽略数据标签信息，导致对数据进行分类时，不能达到理想的分类效果，因此，如何对标签数据进行分类与挖掘的研究具有重要意义[2]。

梁修荣[3]等人提出基于聚类和SVM的长短期浏览行为数据挖掘方法，该方法首先获取数据轮廓系数，把轮廓系数作为类分离度量参数，通过该参数对数据的正、负样本进行聚类与分组。分别对小组进行交叉结合训练，获取不同的SVM分类器，将数据样本与聚类中心间的距离加权结果作为分类器的判断依据，对数据类别进行判断并选取合适的分类器，来实现浏览行为的数据分类与挖掘。但该方法没有对数据进行降维处理，减少了数据存储空间并降低了数据维数，导致分类结果不够准确。张兆晨[4]等人提出基于卷积神经网络的长短期浏览行为数据挖掘方法，该方法首先构建卷积神经网络，根据神经网络结构中的卷积核尺寸，建立玻尔兹曼机模型。通过数据感兴趣区域体素构造数据集，对玻尔兹曼机进行训练，获取相应的权重矩阵，并对该矩阵进行相对变换。将变换结果作为卷积神经网络的初始卷积核参数，最后对整个模型进行训练，获取分类模型，实现浏览行为的数据分类与挖掘。但是该方法没有对数据进行降维处理，无法保留重要信息特征，导致数据挖掘的相对误差较大。张燕[5]等人提出基于异构距离的长短期浏览行为数据挖掘方法，该方法利用聚类算法对浏览行为数据集进行均衡处理，得到均衡的数据子集。针对数据子集，分别建立分类器，通过异构距离对数据集中的样本间距进行计算。最终利用Adaboost算法进行迭代得到分类器，实现浏览行为的数据分类与挖掘。该方法没有对数据进行降维处理，剔除冗余信息，导致数据挖掘的效率较低。

为了解决上述方法存在的问题，提出基于标签映射的长短期浏览行为数据挖掘方法，首先对数据进行降维处理，再结合节点映射构建标签化数据集对长短期浏览行为数据进行训练与学习，实现数据的分类与挖掘。

2 长短期浏览行为数据降维处理

对数据进行降维处理会出现数据信息丢失情况，可通过PCA算法控制数据的损失程度，该算法根据数据本身的相关性对降维后的数据进行保护[6]，详细计算步骤如下：

p=MTk，s.t.MTM=R

(1)

式中，M表示数据转换矩阵，M∈Qr×r′，数据矩阵k通过数据转换矩阵M∈Qr×r′进行转换，得到新的r′维度空间p，R表示单位矩阵。

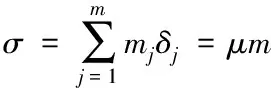
其中，加权系数表示为m=(m1，m2，…，mn)T，σ到m的变换坐标表示为μ，σ的相关矩阵设为L，L的取值已知时，即

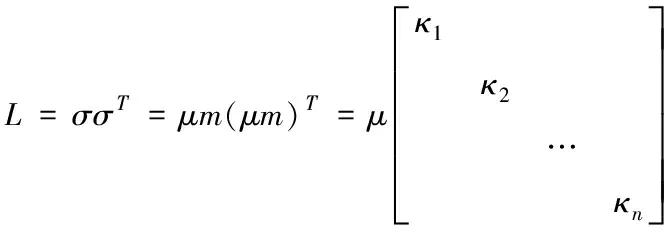
(2)

通常情况下，已知的数据信息通过σ进行表示，由上述可知，L已知，当μμT=R，则R为单矩阵，定义为

Lδj=κjδj

(3)

KL在进行降维变换时，需选取m前面的特征向量，其选取向量个数表示为n′，选取后需去除剩余部分的其它特征向量，即

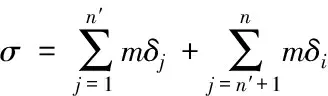
(4)

式中，δj分别表示δi均表示矩阵L的代数特征值与特征分量。

(5)

式中，若n-n′个的特征向量对应的特征值之和最小，则此时均方误差为最小。当最大的特征值所对应的特征向量为n′个时，所构成的n-n′的矩阵表示为μn′，则μn′可取代μ，即mn′=μn′σ，其中，对σ进行降维后所得到的主成分为mn′。

根据上述计算对协方差矩阵进行表示，即

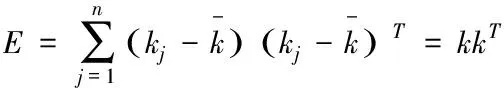
(6)

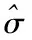
关于式(1)中M的矩阵求解，可通过关于E的特征值所对应的特征向量来实现，关于E的特征值和特征向量的求解如下：

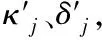
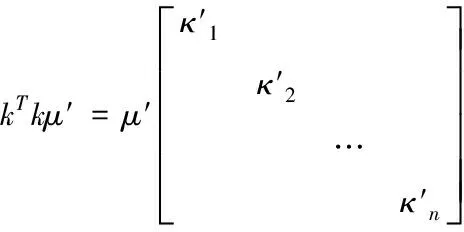
(7)

通过上式获取E与E的转换矩阵间的特征值与特征向量存在的对应关系，完成对数据的降维处理，即

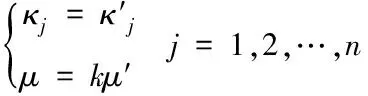
(8)

3 基于标签映射的长短期浏览行为数据挖掘

基于标签映射的长短期浏览行为数据挖掘方法在建立映射层模型与学习层的基础上进行分类与挖掘，其详细步骤如下：

1)映射层

该层次主要是对浏览行为数据节点向量进行转换[7]，通过随机游走的形式对浏览行为数据进行采集，获得与浏览行为相关的数据节点集的序列化表达式[8]。

每个游走序列的最大长度为max-length，整个游走过程需要游走的总次数为walk-times，得到相应节点表示为N，其整个网络数据的游走过程的输出训练集为Trainingset={(N，Enυ(N))}。

当游走产生节点N的周边环境节点时，对参数进行优化，其最终目标函数计算公式为

(9)

上述公式表示模型的最终目标是对游走得到的Enυ训练集进行参数更新迭代运算，使得模型在某参数解的条件下，当前训练集的概率q取值达到最大。节点向量映射过程如图1所示。

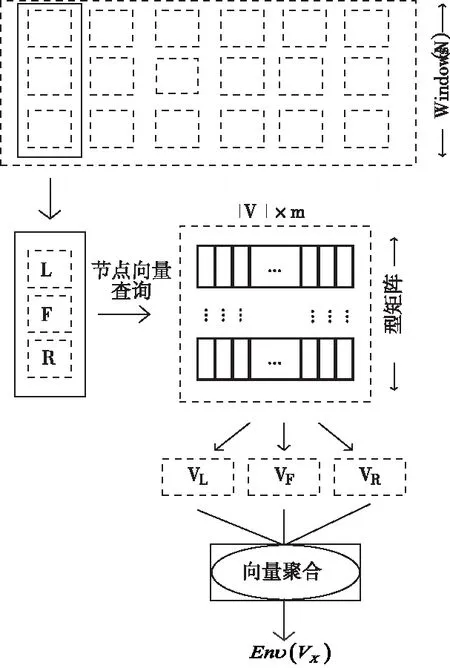
图1 节点向量映射

根据如图1所示，对K节点的周围节点进行取样，对L、F、R节点进行聚合，其聚合运算结果表示K节点的向量序列，通过线性求和聚合原理对节点进行聚合，得到聚合结果Enυ(NK)。对节点向量进行处理时，采用Huffman树对构造的节点进行查询。

叶子节点周边环境的节点向量表示为NEnυ(N)，使用Huffman树对节点进行查询时，此时的叶子节点经过路径的分类概率计算公式如下

(10)

得到最终的优化目标函数为

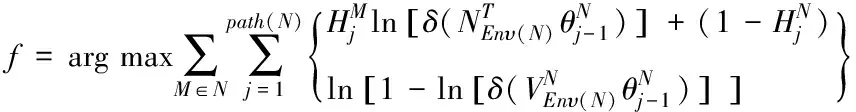
(11)

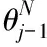
在迭代过程中，为了提高收敛速度以及有效避免迭代算法的梯度消失现象，可引入牛顿表达式l1(K)=wq(K-Ki)l(K)，使l1(K)与l(K)初始值相同，以此为基础对节点向量参数进行迭代，具体计算公式如下

(12)

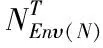
2)学习层

上述层次进行迭代更新，得到网络浏览数据节点的特征矩阵，定义为V，然后对节点向量矩阵相似度进行计算，根据相似度值来判断分类结果。采用余弦相似性指标对节点间的相似值进行计算，从网络数据集的边缘数据集中，选取部分边缘数据集，分别对每个数据集两端进行相似度计算，并与网络数据中无连接关系的节点进行相似度比较，根据节点间的转移概率矩阵对节点相似度矩阵进行计算[10]。

获取浏览数据节点特征，首先对特征节点向量进行处理，通过节点特征建立标签化训练数据集，将节点向量间所构成的新向量分为两个类别，分别为：链接存在与链接不存在，以此为基础对二分类模型进行训练，对测试数据集是否存在链接进行计算与验证。建立标签化训练数据集的步骤如下

(13)

式中，Na、Nb分别为a与b节点的特征向量。则a与b节点所构成的边向量Nab为

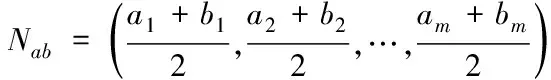
(14)

对边向量的标签进行划分，即

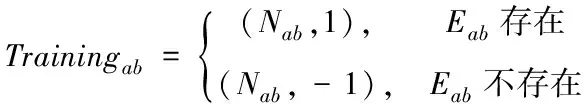
(15)

式中，Eab表示节点a与b构成的边。

分类器的设置可通过SVM二分类方法对不同维数的数据分别进行决策，对于线性可分数据与非线性可分数据，可分别选取合适的策略进行分类[11]。SVM超平面与决策边界示意图如图2所示。

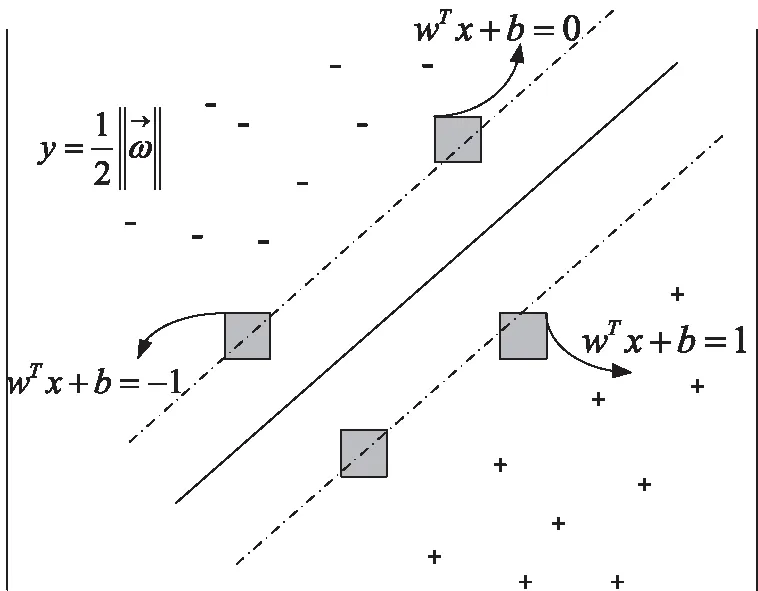
图2 SVM超平面与决策边界

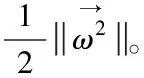
对于线性不可分的数据集，SVM二分类方法需结合核函数进行操作，将原始数据映射到更高维度的空间，在新的维度空间进行线性划分[12]。SVM二分类优化的计算公式为

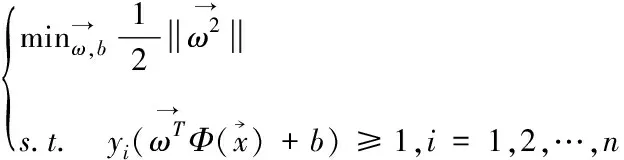
(16)

式中，拉格朗日对偶问题可表示为

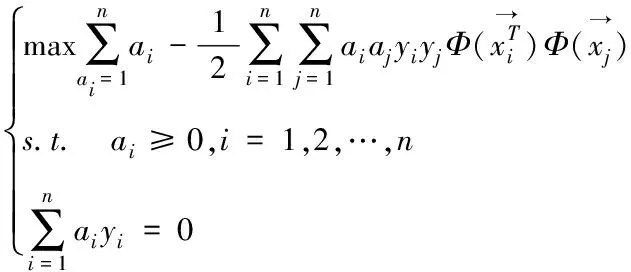
(17)

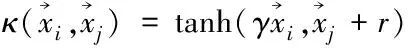
(18)

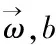
4 实验与结果

为了验证基于标签映射的长短期浏览行为数据挖掘方法的可行性与有效性，需要进行相关实验。本次实验环境为Visual C#，内存为2GB，CPU为PetiumDual 1.6GHz，系统为Windows XP操作系统。本次实验采用基于标签映射的长短期浏览行为数据挖掘方法(方法1)、基于聚类和SVM的长短期浏览行为数据挖掘方法(方法2)、基于卷积神经网络的长短期浏览行为数据挖掘方法(方法3)进行测试，将分类开销、分类时间和分类准确率作为测试指标进行相关测试，具体测试结果如下。

1)分类开销

通过图3对比3种方法的分类开销。

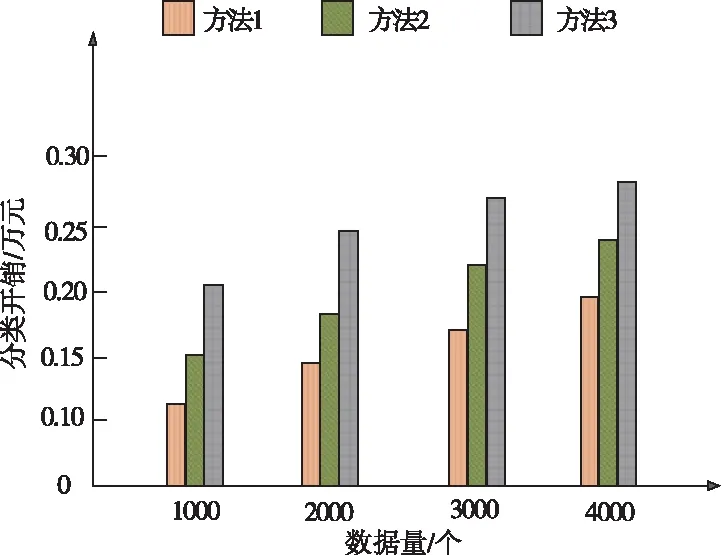
图3 对比不同方法的相对误差

由图3可知，方法1的分类开销低于方法2与方法3，证明方法1的分类开销最小且分类效果更好。因为方法1在对长短期浏览行为数据进行分类时，对数据进行降维处理，去除数据的冗余特征，结合标签映射对数据进行训练学习，进而降低了分类开销，提高了数据挖掘效果。

2)分类时间

通过图4对比3种方法的分类时间。

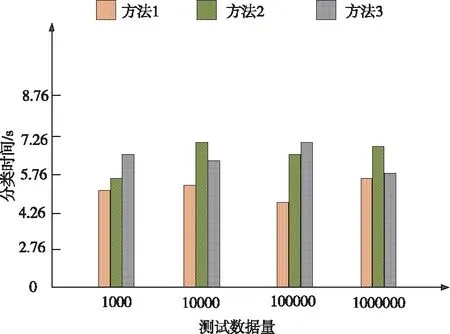
图4 对比不同方法的分类时间

分析图4可知，方法2与方法3的分类时间均高于方法1，证明方法1的分类速度较快且分类效果较好。因为方法1在对长短期浏览行为数据进行分类时，对数据进行降维处理，在数据维数得到降低的同时提高了分类速度，结合标签映射对数据进行分类，达到了数据挖掘的理想效果。

3)分类准确率

通过图5对比3种方法的分类准确率。

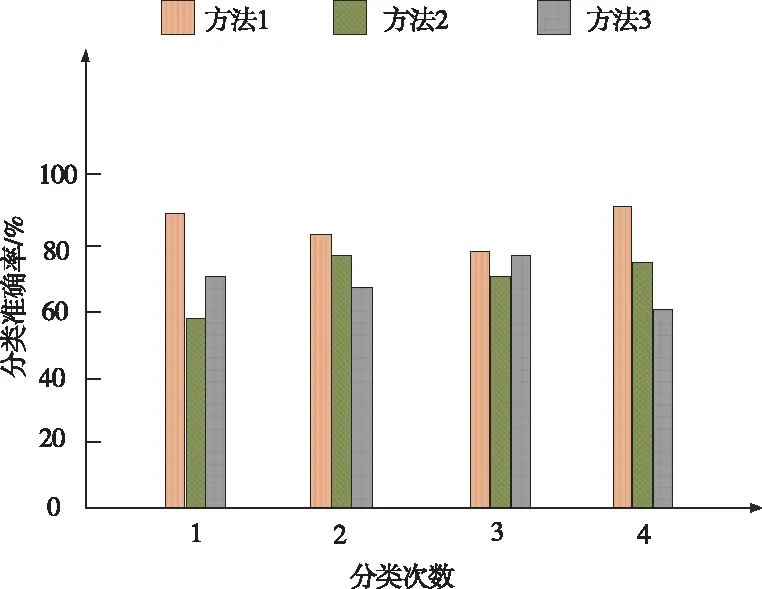
图5 对比不同方法的分类准确率

据图5数据可知，方法1的分类准确率高于方法2与方法3，证明方法1的分类准确性更高。因为方法1在对长短期浏览行为数据进行分类时，对数据进行降维处理，剔除无用信息，有效保留重要信息特征，减少所需存储空间，加快计算速度，使得数据分类及数据挖掘效果更好。

5 结束语

信息技术的发展在网络信息数据全球化的背景下，对数据进行分类在数据挖掘领域中有着广泛的应用。目前数据分类方法在对数据进行分类时，没有剔除数据的冗余特征、降低数据维度、无法保留重要信息特征，导致数据分类结果的相对误差较大、分类时间较长以及分类结果不够准确，为此提出基于标签映射的长短期浏览行为数据挖掘方法，该方法有效解决了当前分类方法中存在的问题，达到了数据挖掘的理想效果。