机场交通需求概率密度预测方法研究

田 文，杨 帆，郭怡杏，宋津津

(南京航空航天大学民航学院，江苏 南京 211106)

1 引言

民航运输网络关联程度日益加强，一旦某机场发生延误，其他关联机场就会产生交通流量波动，需要对其交通需求准确预测，以实施科学的流量调配策略。由于机场交通需求变化存在不确定性，而传统确定性交通需求预测方法较难体现，因此考虑将不确定性纳入交通需求预测。已有预测成果主要围绕三方面展开：一是将不确定性因素，如飞行轨迹、飞行意图等纳入预测过程，建立确定性预测模型或组合预测方法[1，2]；二是量化飞行轨迹[3]、进出扇区时间[4]等随机因素[5]，给出交通需求期望概率区间[6]；三是以单位时间内航空器数量为对象，采用参数估计、半参数估计和非参数估计等方法[7-9]揭示预测结果的随机性[10-12]。上述方法或由于其确定性预测方式较难直观反应不确定性的影响，或限于数据条件需预设随机性分布规律。

针对上述研究不足，创新性地构建了一种基于神经网络分位数回归和核密度估计的机场概率密度预测方法，通过提取不同分位点交通流量变化规律，获得机场交通需求的概率密度分布，以得到具体的点预测值及其变化区间，避免了对需求预设随机性前提下的普适性验证难题。基于广州白云机场的运行数据验证，发现所提方法给出的不确定性区间预测结果要比确定性点预测结果传递更多随机规律性信息，且与BP神经网络预测方法相比准确性更高。

2 机场交通需求概率密度预测方法

2.1 基于神经网络分位数回归及核密度估计的概率性交通需求预测模型

利用神经网络分位数回归[9]来预测机场未来交通需求的分位数，再利用双曲正切函数作为神经网络隐含层函数，把得到的机场交通需求的预测分位数作为核密度估计的输入变量，实现对机场交通需求的概率密度预测。基于神经网络分位数回归的预测模型为

Q(θ|X)=f[x，u(θ)，v(θ)]

(1)

其中，θ为分位点，u(θ)={uij(θ)}i=1，2，…，n；j=1，2…，J为输入层与隐含层之间的待估权重矩阵；v(θ)={vj(θ)}j=1，2，…，J为隐含层与输出层之间的连接权重向量。为达到模型(1)的最后参数估计，可通过优化求解目标函数

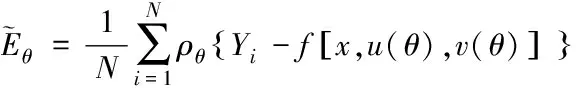
(2)

来实现这一寻优过程。为了使训练的神经网络不进入过度拟合状态，在目标函数加入了相应的惩罚参数项，得到新的目标函数

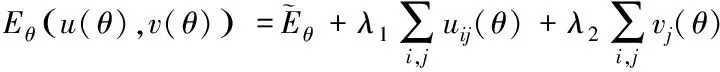
(3)

选用双曲正切函数作为神经网络隐含层核函数，提高交通需求的预测精度

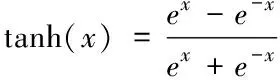
(4)

其中，tanh(x)为神经网络隐含层期望输出值，x为输入变量组成的矩阵。

在概率密度估计过程中，若随机变量分布已知，可直接使用参数估计进行概率密度估计。然而，由于机场实际交通流量数据不符合一定的分布规律，因此采用核密度估计，从机场实际交通流量数据样本出发，根据预测得到的未来一定时段内连续交通流量，得到其连续概率密度曲线图。对于独立同分布随机变量x1，x2，…，xn，服从的概率密度函数f(x)的核密度估计量形如下：

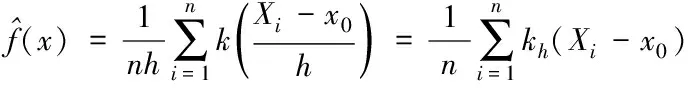
(5)

2.2 机场交通需求概率密度预测方法

对样本数据进行Q-Q图分布检验，如发现样本数据不符合分布假设，则将样本数据输入到神经网络分位数回归模型进行训练，确定神经网络的参数和结构。此过程中，将分位数回归与神经网络结合，可获得不同分位点水平所对应的分位数，作为输入变量代入网络结构中训练，进而得到响应变量条件分位数估计函数，利用核密度估计求其概率密度分布函数及预测值，方法流程如图1。

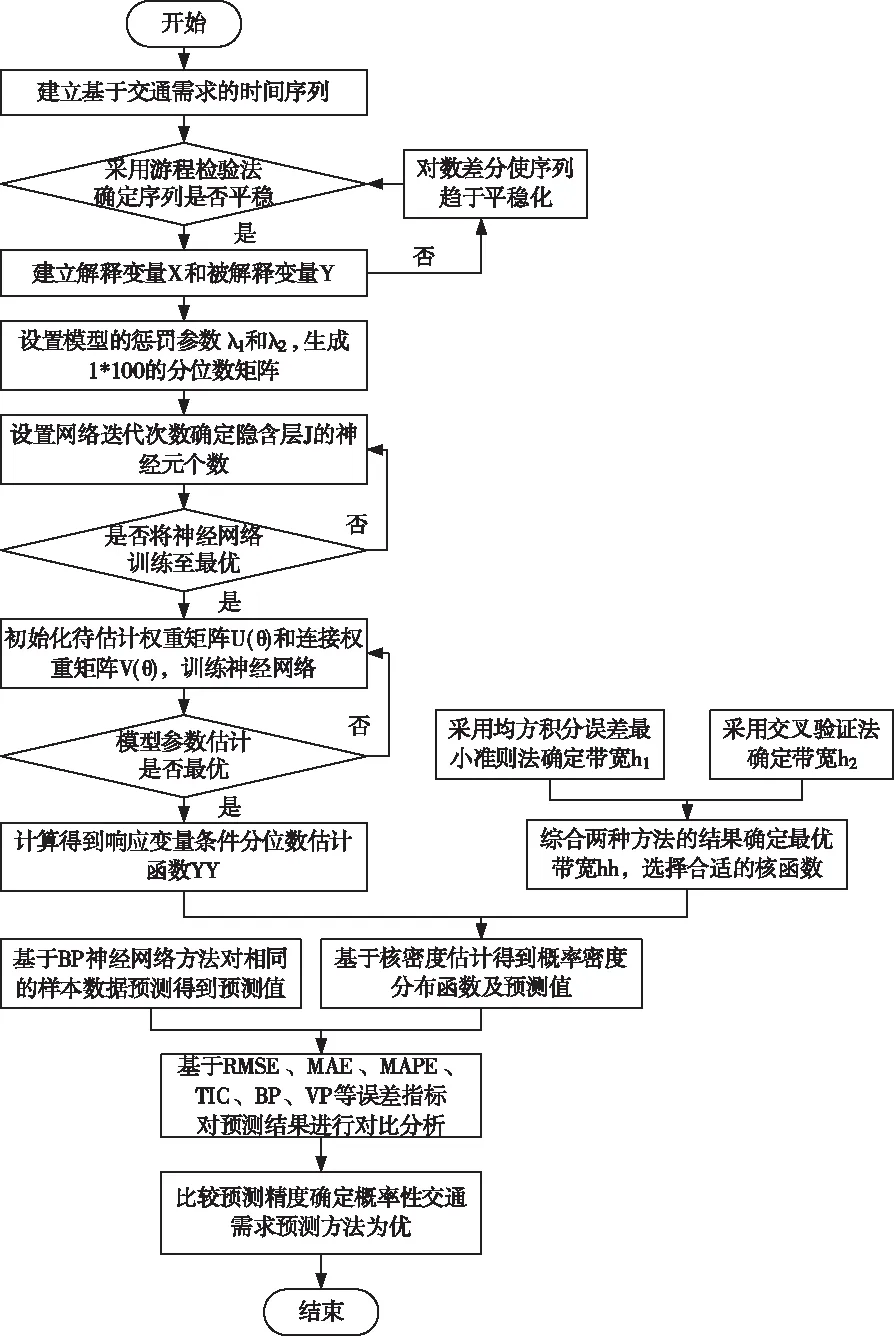
图1 概率密度预测流程图

3 实例分析

3.1 数据来源及样本描述

2019年6月广州白云机场起飞架次、降落架次以及机场气象数据作为样本数据，选取前21日每日9：00-9：15时段每15分钟的交通流量作为输入变量，以22日同时段交通流量作为输出变量，实行滚动预测，共得到2016组样本。对样本数据进行Q-Q图分布检验如图2，发现样本数据不符合正态分布假设，因此采用机场交通需求概率密度预测方法。

图2 样本数据分布检验

将样本数据输入神经网络分位数回归模型进行训练，确定神经网络的参数和结构。本文构建的模型是基于单隐层的神经网络分位数回归，输入层变量数量为21，隐含层变量数量为1，输出层变量数量为1，即神经网络的结构为21-1-1。迭代次数5000次，为防止神经网络分位数回归网络陷入过度拟合，模型的惩罚参数1、2设为0.1，模型中分位数点取[0.0001，0.9999]，间隔0.01，共生成100个分位点。

3.2 实证结果及分析

以2016年6月22日9：00-9：15时段为例，将获得的样本代入神经网络分位数回归模型中进行训练，得到连续的100个条件分位数，将这100个条件分位数代入核密度估计方法中，得到预测当日该15分钟时段内交通需求的概率密度曲线图，随机选取100次预测中6次概率密度分布结果如图3。可以发现，真实值(红色标线)虽未出现在概率密度曲线的最高点附近，但在对该概率密度积分后得到的概率值所对应的预测值(黑色标线)与真实值非常接近。

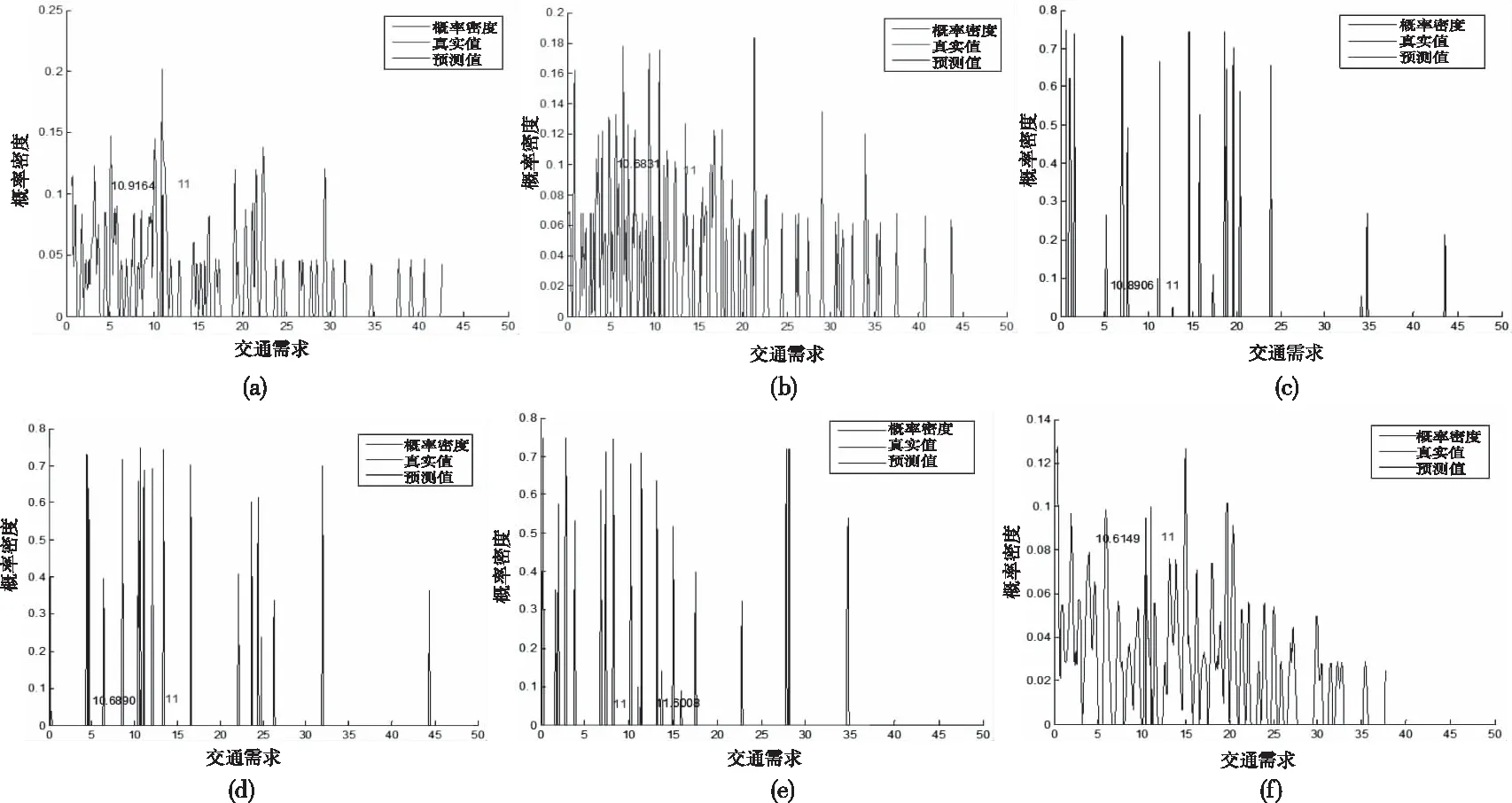
图3 2016年6月22日9：00-9：15广州白云机场交通需求概率密度分布

为更好说明机场交通需求概率密度预测方法准确性，使用传统BP神经网络预测同时段交通流量。对比两种方法的预测结果及其误差，如图4：左图中蓝色曲线代表采用BP神经网络预测方法得到的100个预测值，红色曲线代表采用概率密度预测方法得到的100个预测值，与该时段的真实值11(黑色虚线)对比发现，BP神经网络方法得到的结果波动性较大，概率密度预测方法得到的结果较为稳定，始终围绕在真实值左右。如实际运行中需在此结果中选取预测值，则BP神经网络法得到的结果有可能过于偏离真实值，而概率密度预测方法得到的结果更加准确。

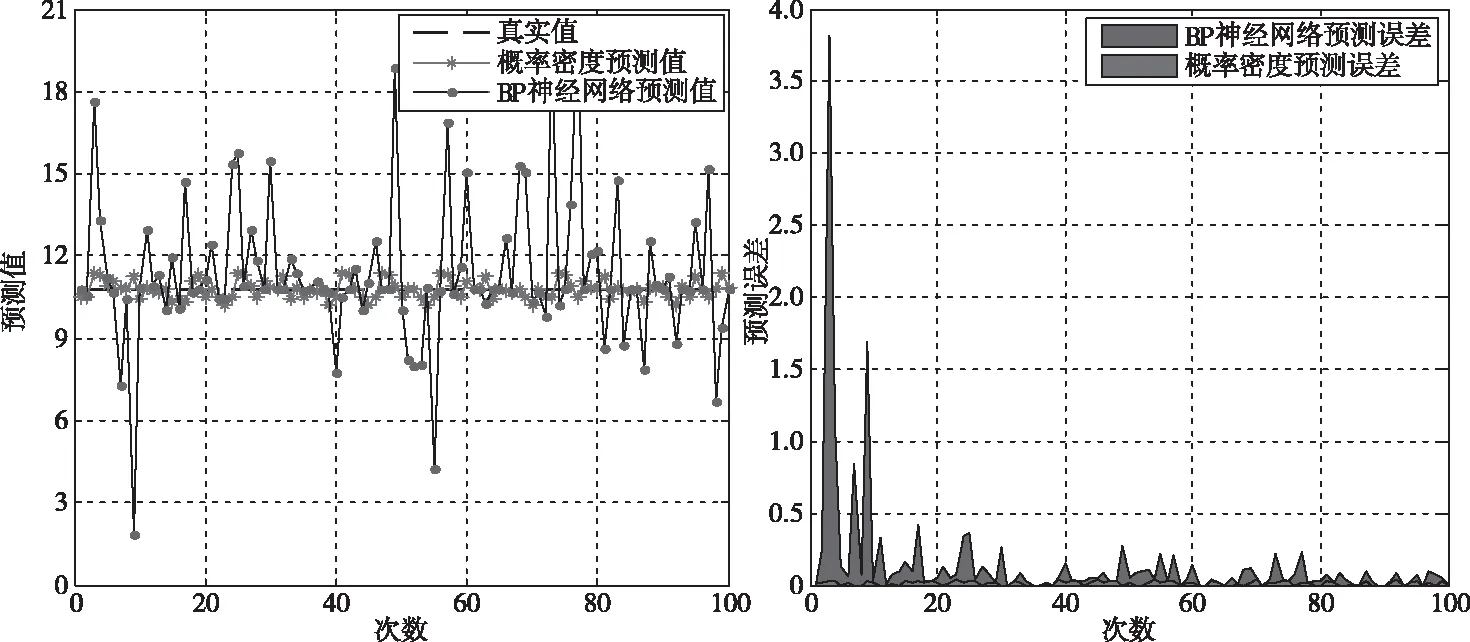
图4 2016年6月22日9：00-9：15广州白云机场交通需求预测值及误差

图4右图中，蓝色阴影部分代表采用BP神经网络预测方法得到的100个预测值所对应的预测误差，红色阴影部分代表采用概率密度预测方法得到的100个预测值所对应的预测误差，两类误差相对比发现：概率密度预测方法结果误差小，基本保持在4%左右；BP神经网络预测方法在预测初期误差偏差大，直到约30次预测后，结果才逐渐稳定地接近真实值，但其准确性仍与概率密度预测得到的结果存在较大差距。说明BP神经网络存在一定学习过程，较难充分满足空管较强的现实时效要求。

4 总结

为更好体现机场交通需求的变化趋势及其对应的概率水平，本文构建了神经网络分位数回归及核密度估计相结合的概率性交通需求预测模型和方法，实现了对机场交通需求预测值变化区间及其发生概率的量化，并利用实际机场运行数据进行了仿真验证，得到结论：①利用所提预测方法对该概率密度积分后，得到的概率值所对应的预测值与真实值非常接近。②所提预测方法结果始终保持较小误差波动，而常用传统BP神经网络预测结果需约30次学习后方能逐渐接近真实值，且偏差较大。