例谈数学竞赛中复数数列问题的解法

徐友伟

(浙江省杭州市建德市寿昌中学，311612)

数学竞赛中的复数数列问题,常以复数的递推关系为载体出现.求解这类问题既要用到复数的概念、性质及运算法则等知识,又要根据递推数列的结构特点运用数列的有关解题技巧,因而综合性较强.下面以近几年全国高中数学联赛试题为例,探究复数数列问题的常见解法.

一、直接递推

分析依据递推公式研究复数数列{zn}相邻项之间的关系,明确求解方向.

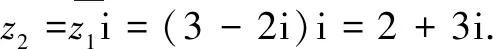
所以z99=z1i50-1=z1i=(3+2i)i=-2+3i,z100=z2i50-1=z2i=(2+3i)i=-3+2i.进而z99+z100=-5+5i.

二、实部、虚部分别递推

分析先设出复数的代数形式,然后将题设递推公式转化为代数形式,通过分别研究实部、虚部的递推关系,将复数数列问题转化为实数数列问题,从而获解.

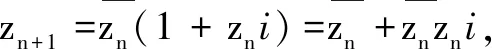
三、转化为复数模进行递推

证明由题意,利用反证法可知zn≠0(n∈N*).

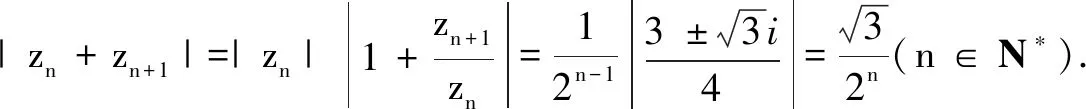
综上，得证.

评注本题将复数数列的递推关系转化为其模的递推关系来研究,在对正整数m分奇偶性讨论的基础上,依据复数模的性质进行放缩法求解,充分考查了学生的化归转化能力和数学抽象、逻辑推理及数学建模等核心素养.