例谈“三会”视角下数学情境问题的解决 *

马 琳 陈算荣

(江苏省扬州大学数学科学学院，225002)

《普通高中数学课程标准(2017年版)》(以下简称“课标”)提出教师在数学教学中要引导学生会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界[1](以下简称“三会”)．“三会”强调了数学与世界的紧密联系,是学生学习数学的终极目标．史宁中教授对“三会”做了进一步阐述:数学的眼光就是数学抽象,数学的思维就是逻辑推理,数学的语言就是数学模型[2]．可见,数学核心素养是“三会”的具体化．考察近几年的高考数学题,不难发现基于情境的数学问题(以下简称“情境题”)开始涌现,通过情境题考查学生的数学核心素养水平是高考命题的一种策略．情境题较之于一般的纯数学背景题,需要学生从实际情境中抽象出其中蕴含的数学问题,也就是具备数学的眼光,显然难度增大．学生在面对不同的情境时,可能会遇到各种各样的困难,因此,学会如何分析情境题至关重要．

“三会”中蕴含着“观察思考表达”这一认识世界的过程,而情境题是考查学生“三会”的一个重要载体,情境题的解决过程亦循着“观察思考表达”的分析框架．具体来说,用数学眼光观察世界是指用数学概念和数学符号去观察客观世界,发现客观世界中的形和量及它们之间的关系[3];要求学生在情境题中从数学的角度将题干中的信息整理出来,弄清条件,分析解决问题需要得到哪些信息．用数学思维思考世界是指用数学知识来推理、证明的思考过程[3];要求学生能根据题中信息有逻辑地思考问题从而有效解决问题．用数学语言表达世界是指用文字语言、图形语言和符号语言来表达客观对象之间的数量关系和空间形式[3];要求学生可以用数学语言将思考过程和解答过程表达出来,最终得到问题的解．

根据问题与情境的融合度不同,情境题可分为五个层次,分别是前结构层次、单点结构层次、多点结构层次、关联结构层次和拓展抽象结构层次,其内涵详见表1[5][5]．

从表1可看出,单点结构层次和多点结构层次的情境题的差别主要在于从题目中提取信息单元的多少,前者情境简单,后者情境熟悉,难度比较接近; 关联结构层次和拓展抽象结构层次的情境题都需要提取多个信息,前者情境陌生,后者需要超越情境,难度也较为相当,后者略高．基于篇幅的限制,下面仅选择代表前结构层次、单点结构层次和关联结构层次的三道高考题,阐述如何从“三会”的视角去分析和解决情境问题．

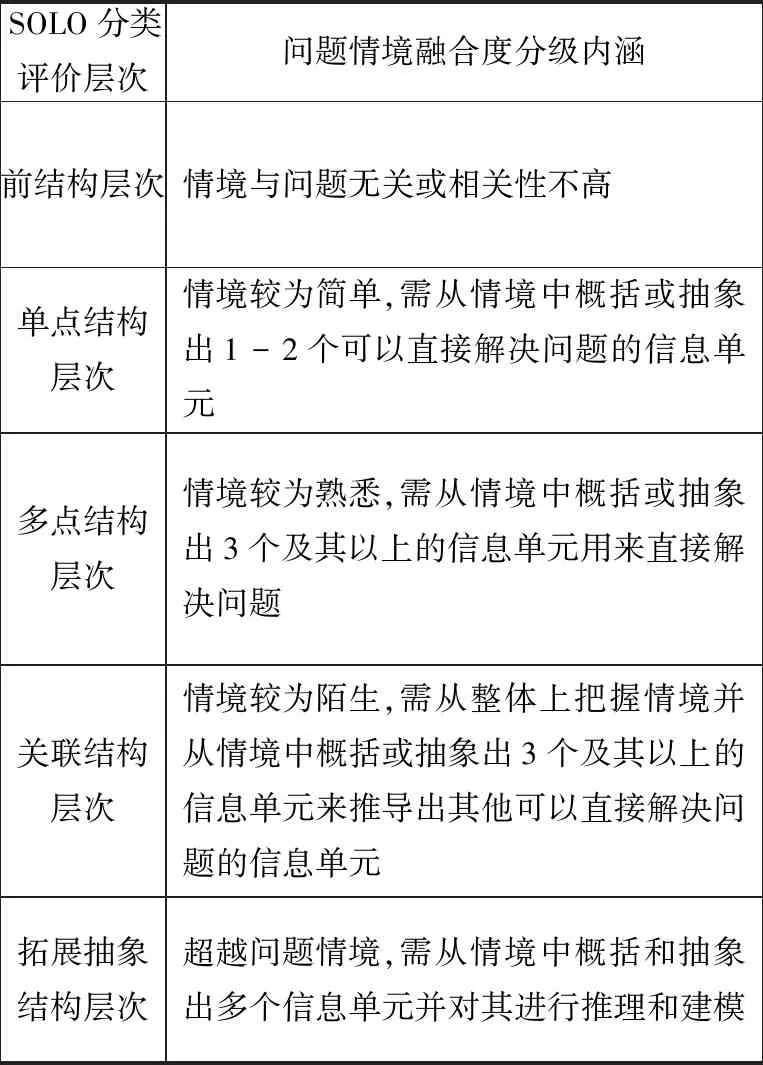
表1 问题情境融合度层次划分

一、前结构层次情境题

(A)346 (B)373 (C)446 (D)473

观察该问题情境是对用三角高程测量法测量珠峰高程的描述,但题目中的三角高程测量法仅是一个背景,与数学问题联系不密切,属于前结构层次情境题．因此,该题的情境不影响学生解题,并且题目为实际的测高情境进行了数学化的抽象配图,所以本题也不需要学生对情境进行数学抽象,只需将文字语言与图片结合起来观察并从中概括出已知和未知信息．已知信息:A′,B′,C′分别是ABC三点在同一水平面的投影,∆A′B′C′中两个角的度数,由点C测得点B的仰角,由点B测得点A的仰角和BB′与CC′的差.未知信息:在图片中没有角或线段表示由点C测得点B的仰角,由点B测得点A的仰角和AA′-CC′.

思考这一环节教师要引导学生思考在图片中如何构造两个仰角和AA′-CC′以及如何求AA′-CC′.首先,教师引导学生根据仰角定义在图中作垂线,从而可以在图中表示出仰角和AA′-CC′.其次,在学生知道如何表示AA′-CC′的基础上,引导学生思考如何在得到的图形中将已知量与未知量转化到∆A′B′C′中,利用解三角形的相关知识得到答案．

表达这一环节要求学生将上述问题思考清楚后用数学语言来表达出来．首先,作出相应辅助线,得到AA′-CC′可以表示成A′B′+100.其次,根据三角函数相关知识得到C′B′的长度．最后,在∆A′B′C′中利用正弦定理求得答案．具体表达如下:

如图2,过点C作CD⊥BB′于点D,过点B作BF⊥AA′于点F,则∠BCD=15°，BD=100，∠ABF=45°，CD=C′B′,A′B′=BF=AF,BB′=FA′,∠C′A′B′=75°.

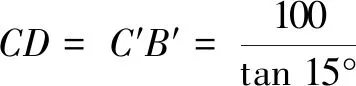
二、单点结构层次情境题

情境问题2(2019年全国Ⅰ卷理科第6题)我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“───”和阴爻“─ ─”,图3就是一重卦．在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是( )

观察该问题情境是以“卦”为背景的文化情境,学生需要在情境中提取出“重卦”的定义,并结合具体的图例信息,进一步理解“重卦”的定义,故学生需要从情境中提取2个信息,并分析这些信息对于解题的意义.本题属于单点结构层次的情境．所以教师要引导学生结合图片中的例子用数学的眼光观察情境中对重卦的描述,提取出已知信息并抽象出概率模型．已知信息:每个重卦中有6个爻、每个爻有阳爻和阴爻两种可能．未知信息:重卦恰有3个阳爻的概率．

思考首先,教师启发学生根据概率的定义,分析求解该问题需要由已知推出哪些所需的中间量,从而引导学生根据已知得出由阳爻或阴爻组成的6个爻有多少种可能,即能构成多少个重卦,以及其中恰好包含3个阳爻的重卦的数量．在此基础上,再引导学生根据排列组合的相关知识,求得这些中间量．

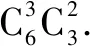
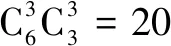
三、关联结构层次情境题

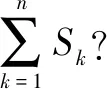
由题意可知,对折3次可得到2.5dm×12dm,5dm×6dm,10dm×3dm,20dm×1.5dm四种规格的图形，对折4次可得到1.25dm×12dm,2.5dm×6dm,5dm×3dm,10dm×1.5dm,20dm×0.75dm五种规格的图形．

四、结束语

鉴于数学问题情境有多种多样,教师在日常教学中不仅要重视情境的创设,让学生感受到生活中处处有数学,而且要重视如何“破解”情境,发现其中蕴含的数学问题和数学模型,让学生领会解决情境问题的要领．“观察——思考——表达”是掌握“三会”的要领,也是情境问题解答的要领．观察是第一步也是极其关键的一步,不仅要观察题目所给的条件,观察图形的结构和图形各要素之间的数量关系和位置关系,有时还需要结合情境加以想象性的观察.例如前面的关联结构层次情境题,学生可以结合语言文字描述进行活动操作想象,并在活动场景想象中加以观察．观察是正确思考的前提,思考则是问题解决的“机关”．思考就是要在已知和未知之间搭建联结的桥梁,将条件与条件进行关联和整合分析,不断生成新的已知,直至把最后要解决的未知变成已知,这样桥梁就自然搭建好了．表达是数学问题情境解决的成果体现,是将观察和思考的成果用数学的方式简洁地、有逻辑地呈现．学生真实地经历“观察

——思考——表达”这一过程,才能真正落实和发展数学核心素养．