也谈一道二元最值问题的解法
2022-02-28彭光焰
彭光焰
(湖北省广水市一中,432700)
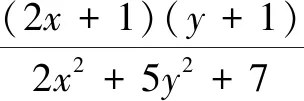
这是江苏省天一中学2019年10月份高三数学调研考试填空题最后一题,文[1][2]对这道试题进行了深入研究,给出了多种精彩的解法,认真学习后收获颇多.但两文给出的方法需要引入多个参数并多次放缩,比较独特,操作性不强,学生不易接受.文[3]给出的导数解法是由高中生提供的,尽管计算量很大,但对高一学生实属不易,说明她自学了导数的有关知识.笔者在此介绍判别式法、基本不等式法、拉格朗日乘数法来解决此类问题,具有可操作性.
思路1分式的分子和分母最高次数都是二次,可以考虑用判别式法求解决.
解法1判别式法
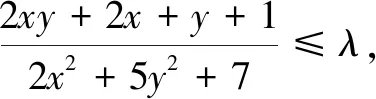


思路2拉格朗日乘数法是解决二元函数最值的有效方法,可以考虑用拉格朗日乘数法来解决此问题.
解法2拉格朗日乘数法

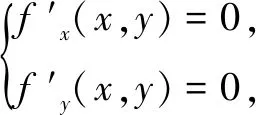
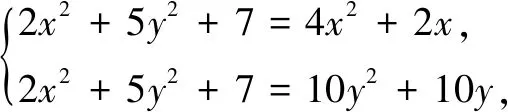

在工程建设阶段,应根据工程的进度和质量,尽量控制施工成本。由于施工内部结构复杂,施工过程繁琐,对施工过程的管理要求较高。选择技术优良、管理体系完善、信誉良好的施工单位和监理单位。监督资格需要更仔细地评估。选择有影响力的建筑单位。完善的施工管理体系能有效实施施工企业流程控制,能顺利完成施工成本动态管理。在选择施工所需原材料时,需要对制造商和市场进行详细的市场调查,确定最合适的采购计划,选择合适的供应商,加强对材料的检验和管理。
思路3由拉朗日乘数法得到当x=2,y=1时原式有最大值,启发我们用基本不等式求最大值.
解法3基本不等式法
由x>0,y>0,得2x2+5y2+7=(x2+4y2)+(x2+4)+(y2+1)+2≥4xy+4x+2y+2=2(2xy+2x+y+1)>0,等号当且仅当x=2,y=1时成立.


下面用此方法来解决文[3]中的题2.

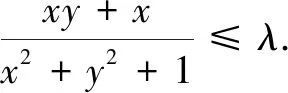

先视上式为关于x的一元二次不等式,得λx2-(y+1)x+λy2+λ≥0,由题意可知Δ1=(y+1)2-4λ(λy2+λ)≤0.
再视Δ1≤0为关于y的一元二次不等式,得(4λ2-1)y2-2y+4λ2-1≥0,由题意可知4λ2-1>0,且Δ2=4-4(4λ2-1)2≤0.

解法2由条件及基本不等式,可得

