高三数学综合测试

一、单项选择题(本大题共8小题，每小题5分，计40分)

1. 已知集合A={x|y=lg(x-2)},B={x|x2-4x<0},则(RA)∩B=( )

(A)(-∞,2] (B)(0,2]

(C)(2,4) (D)[2,+∞)

3.已知函数y=f(x)的部分图象如图所示,则函数y=f(x)的解析式可能是( )

(C)y=sinx-xex(D)y=sinx-xcosx

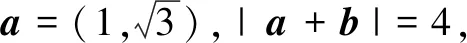
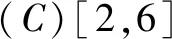
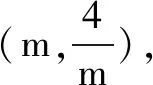
(A)-2 (B)1 (C)2 (D)8

6.某学校社会实践小组共有5名成员,该小组计划前往三个红色教育基地进行“学党史,颂党恩,跟党走”的主题宣讲志愿服务.若每名成员只去一个基地,每个基地至少有一名成员前往,且甲、乙两名成员前往同一基地,丙、丁两名成员前往不同基地,则不同的分配方案总数有( )

(A)86种 (B)64种 (C)42种 (D)30种

(A)x>y>z(B)z>x>y

(C)x>z>y(D)y>z>x

8.由倍角公式cos 2x=2cos2x-1,可知cos 2x可表示为cosx的二次多项式,对cos 3x,我们有cos 3x=cos(2x+x)=cos 2xcosx-2sinxcosxsinx=4cos3x-3cosx,故cos 3x也可以表示为cosx的三次多项式.一般地,存在一个n次多项式Pn(t),使得cosnx=Pn(cosx),这些多项式Pn(t)称为切比雪夫(P.L.Tschebyschelf)多项式.(提示:18°×3=90°-18°×2)

如图,在等腰∆ABC中,已知∠ABC=54°,AB=AC,且∆ABC的外接圆半径OC=1,结合上述知识,可得BC=( )

二、选择题(本题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)

(C)函数g(x)为奇函数

10.已知(1-2x)2 021=a+a1x+a2x2+…+a2 021x2 021,则( )

(A)展开式中所有项的系数和为-1

(B)展开式中二项系数最大项为第1 010项

(D)a1+2a2+3a3+…+2 021a2 021=2 021

11.若实数x,y满足x>y>0,则使得x-y<1成立的一个充分不必要条件是( )

(A)x+y<1

(B)log2x-log2y<1

(C)sinx-siny<1

(D)4x-2·4y<0

12.观察如下数阵:

第1行 1 2

第2行 1 3 2

第3行 1 4 3 5 2

第4行 1 5 4 7 3 8 5 7 2

… …

第n行 1x1x2… … … … … … …xk2

该数阵特点:在第n行每相邻两数之间都插入它们的和得到第n+1行的数,n∈N*.设第n行数的个数为an,第n行的所有数之和为Sn,则( )

(A)an+1=2an-1

(B)Sn+1=3Sn-3

(C)Sn=3[(n-1)2+1]

(D)k=2n-1-1

三、填空题(本题共4小题,每小题5分,计20分)

14.写出满足条件“函数y=f(x)在(0,+∞)单调增,且f(xy)=f(x)+f(y)”的一个函数f(x)=______.

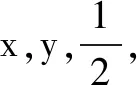
四、解答题(本题共6小题,计70分.解答时应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)为推动实施健康中国战略,树立国家大卫生、大健康观念,手机APP也推出了多款健康运动软件,如“微信运动”,某运动品牌公司140名员工均在微信好友群中参与了“微信运动”,且公司每月进行一次评比,对该月内每日运动都达到10 000步及以上的员工授予该月“运动达人”称号,其余员工均称为“参与者”.下表是该运动品牌公司140名员工2021年1月-5月获得“运动达人”称号的统计数据:

月份12345 “运动达人”员工数1201051009580

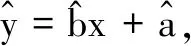
(2)为了进一步了解员工们的运动情况,选取了员工们在3月份的运动数据进行分析,统计结果如下:

运动达人参与者合计 男员工60m80 女员工n2060 合计10040140

请补充上表中的数据(直接写出m,n的值),并根据上表判断是否有95%的把握认为获得“运动达人”称号与性别有关?

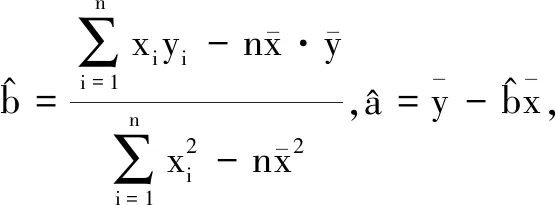
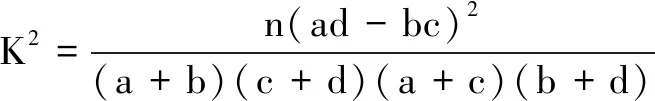
P(K2≥k)0.100.050.0250.001 k2.7063.8415.0246.635

18.(本小题满分12分)已知各项均为正数的数列{an},{bn}满足a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列.

(1)求a的值;

(2)求cos∠DAE的值.

20.(本小题满分12分)为落实立德树人根本任务,坚持五育并举全面推进素质教育,某校举行了乒乓球比赛,其中参加男子乒乓球决赛的12名队员来自高一年级3人,高二年级4人,高三年级5人.本次决赛的比赛赛制采取单循环方式,即每名队员进行11场比赛(每场比赛都采取5局3胜制),最后根据积分选出最后的冠军,亚军和季军.积分规则如下:每场比赛5局中以3∶0或3∶1获胜的队员积3分,落败的队员积0分;而每场比赛5局中以3:2获胜的队员积2分,落败的队员积1分.

(1)比赛结束后冠亚军恰好来自不同年级的概率是多少?

(1)求证:k1k2为定值;

(2)若k1=3k3,求∆FMN的周长.

22.(本小题满分12分)已知函数f(x)=lnx-ax+1,a∈R.

(1)当a=1时,求函数f(x)的最大值;

参考答案

一、单项选择题.

1. B;2. A;3. D;4. C;5. C;

6. D;7. C;8. A.

二、多项选择题

9. BC;10. AC;11.AD;12.ABD.

三、填空题

四、解答题

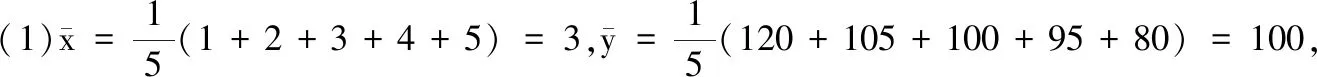
令x=6,得y=-9×6+127=73,即该运动品牌分公司6月份获得“运动达人” 称号的员工数为73.

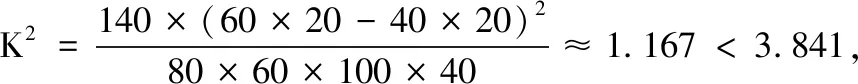
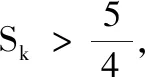
(2)X的可能取值为0,1,2,3.

X0123 P1988116811627

若t=2,则直线l经过右顶点B(2, 0),与题意不符,舍去.所以t=-1,直线l的方程为x=my-1,恒过椭圆C的左焦点F′(-1, 0).

所以,FMN的周长为FM+MN+NF=FM+MF′+NF′+NF=2a+2a=4a=8.

若1-a≥0,即a≤1,则g′(x)≥1-a≥0,g(x)在[1,+∞)单调增,有g(x)≥g(1)=0.故a≤1符合题意.

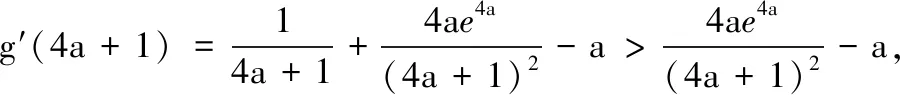
综上,实数a的取值范围为(-∞,1].

○单谈数学○

编者按

单墫，数学家，数学教育家，教授，博士生导师，我国著名数学传播、普及和数学竞赛专家。1964年扬州师范学院数学系毕业，从事数论及数学课程与教学论研究，在数学普及与数学竞赛方面，倾注了大量的时间和精力，培养了一批活跃在我国数学教育前沿领域的专家学者。精彩的辅导讲座、高水平的普及读物，受到数学爱好者的喜爱。

作为扬州大学的杰出校友，单墫老师长期关心《初中数学教与学》、《高中数学教与学》，指导期刊选题、编辑和出版，并亲自为期刊选题、编辑和出版，并亲自为期刊撰稿。数十年来，单墫老师笔耕不懈，坚持每天解题。长期的解题实践形成了“要享受到解题的乐趣”；“要有充足的信心、坚韧不拔的毅力”；“从简单的做起”；“从不同的角度看问题”；“引入适当字母，向基本量靠拢”；“力求简单自然，直剖核心”；“设法创造条件，不断变更问题”等著名的解题原则。为了更好地传播单墫老师的数学解题思想和实用、优质的解题方法，本刊不定期设置“单谈数学”栏目，以飨读者。