均匀设计和模糊数学优化茯苓海棠果果糕配方

周慧，胡永金，陶亮，高斌，付晓萍，田洋

（云南农业大学食品科学技术学院，云南 昆明 650201）

茯苓，多孔菌目茯苓属菌类，是一种药食同源食品。含有多糖、三萜类、脂肪酸、甾醇、酶等生物活性成分[1]，具有抗肿瘤[2]、免疫调节、抗炎、抗氧化[3]、抗衰老、抗肝炎和抗血热等作用[4]，作为中药使用已有两千多年的历史。丽江海棠果，原名丽江山荆子，是来自蔷薇科苹果属丽江山荆子的果实[5]，纳西语叫“多利久补”，是治肾炎、糖尿病的药食兼用的干果。其富含黄酮和多糖等活性成分[6]，具有抗肿瘤[7]、抗氧化[8]、抑菌[9]等功效。目前市场上对海棠果产品开发主要有果醋[10]、果汁[11]、果酒[12]、果酱[13]、酸奶[14]、酵素[15]、油[16]，但在丽江，海棠果主要是鲜食或加工成果干，缺乏深加工。

果糕是我国一种传统糕类食品，属于蜜饯类制品，也是水果深加工的重要形式之一。但我国传统果糕含糖量较高[17]，不符合现代社会健康食品的消费趋势。丽江海棠果和茯苓都具有一定的功能性，所以本次试验以其为原料，选择零热量、抗龋齿的赤藓糖醇代替部分白砂糖研制低糖果糕，为丽江海棠果和茯苓的深加工发展提供技术参考。

目前，多数食品配方优化采用正交试验设计或响应面方法，比较适合因素较少、水平数较少的研究，面对多因素、多水平研究时，试验次数将会大幅度增加，而均匀设计法可在最少试验次数基础上，灵活增加因素水平个数，辅助电脑进行优化处理与验证。此外，常用的感官评价方法也集中在“百分制”法，易受评价员主观影响，因此选择更加客观、合理的评判方法[17-19]对产品感官特性进行评价显得更有意义。研究表明借助模糊数学原理可将复杂的食品感官评价用精确的数学方法来处理，更适合多因素多评价指标问题的解决；同时均匀设计方法的数据也易于计算机处理分析，获得的模型结果可靠、客观性强。本试验采用均匀设计法与模糊数学法相结合，对茯苓海棠果果糕配方进行优化处理，该联用的方法可为茯苓海棠果果糕的生产提供科学依据，也有助于推动食品配方优化研究领域的发展。

1 材料与方法

1.1 材料与试剂

丽江海棠果果干：丽江拓农基地；食盐：云南省盐业有限公司；白砂糖：昆明香冠食品有限公司；茯苓粉：市售；赤藓糖醇、琼脂、卡拉胶、黄原胶、苹果酸、无水柠檬酸：昆明顺佳有限公司。

1.2 仪器与设备

榨汁机（C93T）：九阳股份有限公司；高速多功能粉碎机（JP-800B）：永康市久品工贸有限公司；电子分析天平（AX223ZH/E型）：奥豪斯仪器（常州）有限公司；小熊搅拌机（LLJ-A10T1）：广东小熊电器有限公司；手持折光仪（LB90T型）：广州市速为电子科技有限公司。

1.3 方法

1.3.1 茯苓海棠果果糕的制备工艺流程

海棠果果干→清洗去梗→去涩→漂洗→软化→打浆→过滤→加入茯苓粉、混合糖、复合凝胶剂、复合酸等熬制浓缩→倒模成型→烘制→冷却→成品→包装

1.3.2 操作要点

1.3.2.1 海棠果果泥制备

选择优质海棠果果干，将其清洗、去梗，置于4%氯化钠溶液中预煮10 min脱涩后用清水浸泡1 h去盐。于沸水中加热20 min软化，以干果与水质量比1∶4为定比，打浆后过40目滤网得到海棠果果泥。

1.3.2.2 熬制浓缩

称量果泥、混合糖（赤藓糖醇、白砂糖）、茯苓粉、复合凝胶剂（琼脂、卡拉胶、黄原胶）、复合酸（柠檬酸、苹果酸）后加热进行浓缩。为防止出现气泡，熬煮时先大火后小火，加热过程中不断搅拌使其均匀且预防糊锅。每隔一段时间用手持折光仪测量可溶性固形物含量。

1.3.2.3 倒模烘制

将熬煮浓缩后的果泥趁热倒入模具中，室温25℃静置冷却成型，脱模后按试验设计放入55℃烘箱中烘烤，干燥过程中将其翻转2次～3次。烘烤结束后室温25℃冷却，密封包装得到成品。

1.4 茯苓海棠果果糕的单因素试验设计

以海棠果果泥100 g为基准，固定白砂糖含量，以茯苓粉添加量（1%～5%）、赤藓糖醇添加量（10%～50%）、苹果酸∶柠檬酸质量比（1∶3～3∶1）、复合酸添加量（0.1%～1.1%）、复合凝胶剂琼脂∶卡拉胶∶黄原胶质量比（2∶1∶2、2∶2∶1、1∶1∶1、1∶2∶2、1∶2∶1）、复合凝胶剂添加量（0.5%～2.5%）、熬煮终点可溶性固形物含量（45%～65%）、烘烤时间（13 h～21 h）为因素，以感官评分为指标，开展单因素试验。

1.5 茯苓海棠果果糕的配方优化设计

在确定茯苓海棠果果糕的基本配方成分基础上，结合预试验和单因素试验范围，经分析后开展选择性均匀试验，因素水平见表1。

表1 均匀设计试验因素水平Table 1 Factors and levels used in uniform design

1.6 模糊数学模型的建立

1.6.1 因素集、评语集和权重的确定

评价因素集U是研究产品感官质量构成因素的集合。本研究中，应用模糊数学原理建立感官评价系统[18-19]，产品模糊评价的重点是以组织形态、色泽、酸甜度、风味和口感5个要素进行评定，即评价因素集U={组织形态 u1；色泽 u2；酸甜度 u3；风味 u4；口感 u5}。

评语集V是邀请10位专业评定人员组成感官评定小组对评价指标反馈信息的集合，可用文字、具体数值或等级表示。本研究中，对每个因素按优、良、中、差等级评价，即评语集定位为 V={优 v1；良 v2；中 v3；差 v4}，并将其分别赋值为90、80、70、60分。感官评价标准见表2。

表2 感官评价标准Table 2 Sensory evaluation standard

权重是每个因素在被评价因素中的影响和地位。本试验随机找10位评定员采用二次对比决定法[20]确定5种因素的权重，两两比较时重要的因素得1分，反之得0分，与自身比较时记1分。权重即各项指标与总分之比，即 W={组织形态 W1；色泽 W2；酸甜度 W3；风味 W4；口感 W5}，其中 W1=0.23；W2=0.12；W3=0.19；W4=0.23；W5=0.23。权重评分结果见表3。

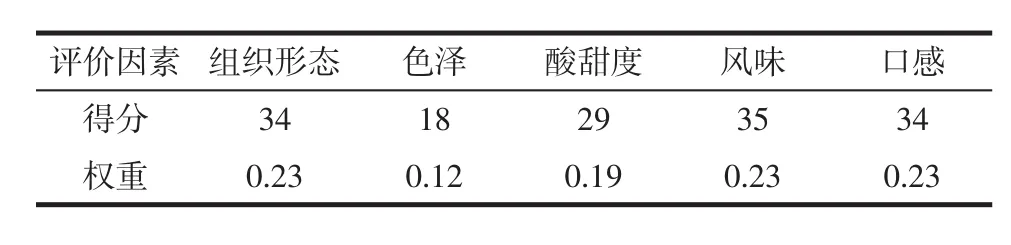
表3 权重评分结果Table 3 Weighted score results

1.6.2 感官评分的计算

食品感官指标综合评判的结果用R表示。R是权重W和模糊矩阵A的合成。即R＝W·A，即产品不同指标、不同等级评价人数。

采用普通矩阵乘法计算综合隶属度R，隶属度R的各个量分别乘以赋值，优、良、中、差依次赋予分值90、80、70、60分，并进行加和，从而得到每个样品的感官评分。

1.7 数据处理

试验数据用SPSS24.0和Microsoft office Excel 2010软件进行数据分析。

2 结果与分析

2.1 模糊数学评价结果

2.1.1 模糊数学感官评分统计结果

由10名感官评定员对试验方案样品的组织形态、色泽、酸甜度、风味、口感等进行感官评定选择，统计汇总后结果见表4。

表4 感官评定票数统计分布Table 4 Vote distributions of sensory evaluation

2.1.2 建立模糊矩阵

将票数折算成赞成的比率，得到模糊矩阵Aj。

以试验1号组织形态为例，5人选择优，5人选择良，中和差无人选择，因此得到组织形态=（5，5，0，0）；同理可得色泽=（3，7，0，0）；酸甜度=（6，3，0，1）；口感=（9，0，0，1）。

2.1.3 模糊变换综合评价结果

依据模糊综合评判数学模型原理，采用矩阵乘法计算规避因取大取小算法产生的误差。

以试验1号样品为例:

将综合评判结果的每个量分别乘以其对应的分值相加可得出样品的最后总得分，试验1号总得分为0.610×90+0.325×80+0.000×70+0.065×60=84.80。同理可得2号～10号感官评分。综合评判结果见表5，模糊数学感官评分最高为84.90。

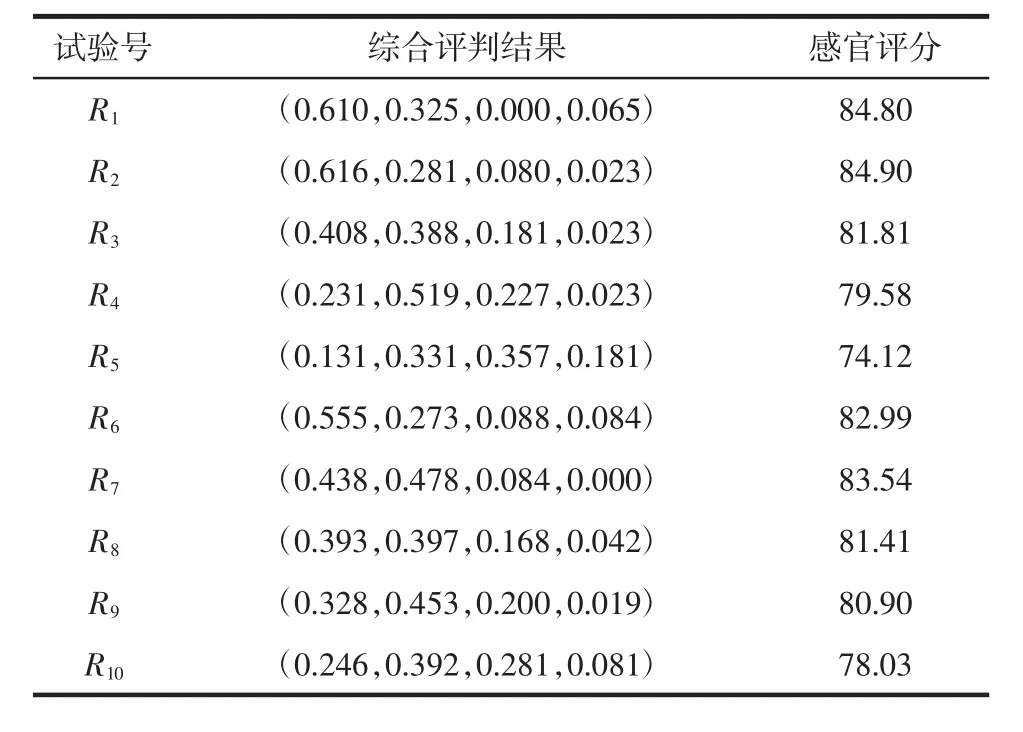
表5 综合评判结果和感官评分Table 5 Comprehensive evaluation result and the sensory score

2.2 多元线性回归模型和多元二项式回归模型分析

使用SPSS24.0统计分析软件进行多元回归分析[21]，分别设定自变量茯苓粉添加量（x1）、赤藓糖醇添加量（x2）、苹果酸∶柠檬酸质量比（x3）、复合酸添加量（x4）、复合凝胶剂添加量（x5）、熬煮终点可溶性固形物含量（x6）、烘烤时间（x7）和因变量感官评分（y），方差分析见表6。

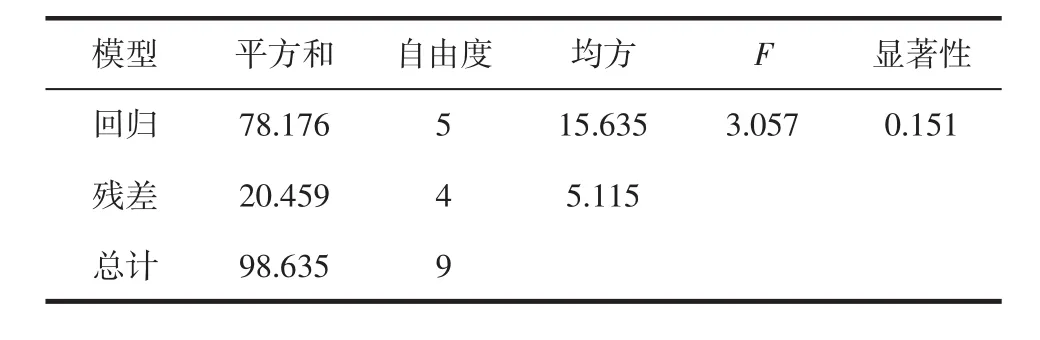
表6 方差分析Table 6 Variance analysis of regression model

由表6可知，方差分析显著性结果P=0.151＞0.05，说明使用多元线性回归模型不能显著性地分析自变量与因变量之间的变化，需考虑使用多元二次多项式回归模型。

在 SPSS24.0 中分别设定 x1、x2、x3、x4、x5、x6、x7，x12、x22、x32、x42、x52、x62、x72为自变量，y 为因变量。再次进行多元回归分析，结果见表7～表9。

表7 多元多项式回归模型摘要Table 7 A summary of the multi-polynthic regression model

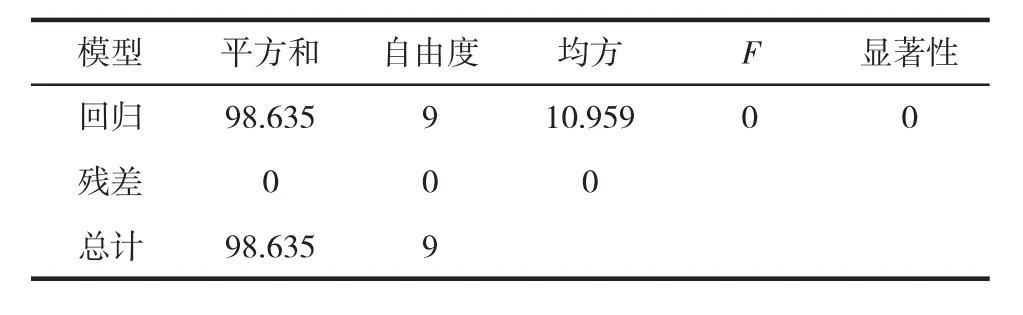
表8 多元线性回归方差分析Table 8 Multilinear regression variance analysis

表9 多元多项式回归模型偏相关系数Table 9 Partial correlation coefficients for multiple polynotion models

由表7～表9可知，复相关系数R=1.000、决定系数R2=1.000，且具有显著性，表明该回归模型能较好地解释自变量与因变量之间的关系，即该多元化多项式回归模型比较适用于当前条件下描述自变量与因变量的线性关系。因赤藓糖醇添加量（x2）、复合凝胶剂添加量（x5）、熬煮终点可溶性固形物含量（x6）、烘烤时间（x7）和复合凝胶剂添加量的平方（x52）的容差为0，其存在严重的共性情况，故被排除。

回归方程确定为y=131.071-4.868x1+1.921x3+8.493x4+0.675x12-0.018x22-0.534x32-5.963x42-0.011x62+0.031x72。

2.3 最佳方案的确定与分析结果验证

通过Excel“规划求解”分析回归方程，确定最优方案：茯苓粉添加量2.5%，赤藓糖醇添加量15%，琼脂∶卡拉胶∶黄原胶质量比1∶2∶2，复合凝胶剂添加量1.5%，苹果酸与柠檬酸质量比1.80∶1，复合酸添加量0.71%，熬煮终点可溶性固形物含量54%时，烘烤时间19 h，其感官评分预期值y为102.94，远远高于直观分析法获得较优方案值R2。因为多元回归模型的多样性，需要进行验证判断，采用方程运算法，对优化结果进行验证，将直观分析法得出的最优试验组R2数值带入回归方程中得出运算结果为86.59，低于回归分析获得的试验结果值，表明回归模型合理、可靠。

3 结论

在茯苓海棠果果糕配方优化研究中，采用均匀法建立了数学模型：y=131.071-4.868x1+1.921x3+8.493x4+0.675x12-0.018x22-0.534x32-5.963x42-0.011x62+0.031x72，该方程能较好预测产品品质随各参数变化的规律，经验证该数学模型可靠。借助该模型得到最佳配方：茯苓粉添加量2.5%，赤藓糖醇添加量15%，琼脂∶卡拉胶∶黄原胶质量比 1∶2∶2，复合凝胶剂添加量1.5%，苹果酸与柠檬酸质量比1.80∶1，复合酸添加量0.71%，熬煮终点可溶性固形物含量54%时，烘烤温度55℃，烘烤时间19 h，此时可获得风味独特、品质上佳的海棠果果糕产品。