一种基于混合硬化本构模型的汽轮机轮盘榫槽疲劳寿命预测方法

唐 晶，王恭义，程 凯，叶笃毅

(1.浙江大学 能源工程学院，浙江 杭州 310027； 2.上海汽轮机厂有限公司，上海 200240)

1 前 言

转子轮盘作为汽轮机核心部件之一，在服役过程中通常承受脉动交变载荷作用，因此轮盘榫槽齿根往往承受一定的拉伸平均应力(如图1所示)。近年来，由于汽轮机中末级长叶片的应用使得叶片离心载荷显著增加，由此导致了轮盘榫槽缺口部位的最大应力可能接近甚至超过材料屈服极限[1]。由于榫槽齿根部位出现明显塑性变形，将导致上述拉伸平均应力出现循环松弛现象。

图1 轮盘榫槽载荷谱及其局部应力应变历程Fig.1 Loading spectrum and local stress and strain response of the groove notch

目前工程中通常采用经验公式(如：Landgraf、MaxWell等[2])来描述材料的平均应力松弛行为。为了拟合上述经验公式中的材料参数，需要预先开展大量非零平均应力下的疲劳实验，这在实际应用中将耗资费时[3]。而且现有的经验公式通常只是对平均应力循环松弛行为的单纯数学拟合，缺乏对平均应力松弛物理机制的深刻揭示。因此，往往会因研究对象不同，其拟合精度出现较大的波动，从而对后续疲劳寿命预测结果产生较大影响[4]。为了克服上述经验公式的不足，近年来，许多学者引入了循环本构模型对材料平均应力松弛行为进行描述。例如，Arcari等[5]采用Jiang与Wetzel动态本构模型模拟了变幅加载下7075和7249铝合金的迟滞迴线及平均应力松弛行为，其模拟精度较经验公式有了显著提升。Rezaiee-Pajand[6]，Mahmoudi[7]等采用多级背应力+线性项的本构模型对循环迟滞迴线及棘轮效应进行模拟，也取得较好的结果。最近，Kourousis等[8]在Chaboche模型基础上提出mMAFM模型，并采用计算软件开展了7075铝合金的循环平均应力松弛模拟与疲劳寿命预测。同样，廖异、曾详国等[9]也采用Chaboche模型对平均应力松弛过程进行本构描述，并推导了Chaboche本构模型的增量形式，最终结合Morrow模型预测了AZ91E-T6镁合金的疲劳寿命。由于动态本构模型基于力学原理，具有明确的物理意义，且能够描述材料瞬态力学响应等优点，因此，在结构疲劳寿命预测中呈现广阔的应用前景[10]。

本研究主要针对某新型汽轮机转子轮盘榫槽的抗疲劳设计需要，基于局部应力、应变法，并结合混合硬化本构模型(N5L1)[11]，研究了轮盘榫槽齿根局部平均应力循环松弛行为，并最终建立了一种考虑榫槽齿根平均应力动态松弛的转子轮盘疲劳寿命预测方法，为汽轮机转子轮盘抗疲劳设计和服役安全性评估提供更为精确的定寿方法。

2 基于混合硬化本构模型的转子轮盘榫槽疲劳寿命预测方法

2.1 混合硬化本构模型(N5L1)简介

在Chaboche随动硬化律[12-13]中，一般考虑屈服面遵循Von Mises屈服准则。图2给出了混合硬化律中屈服面的运动规律。根据塑性流动准则，塑性流动受到弹性区域的约束，发生在加载面内，即f≤0，因此，屈服面可表示成：

图2 屈服面的运动演化规律Fig.2 Evolution law of the yield surface motion

f=J(σ-X)-R-k=0

(1)

式中：随动硬化变量X与各向同性变量R分别表示屈服面的位置与大小，k表示初始屈服面大小。

根据Von Mises屈服准则，式(1)中函数f只与应力偏量第二不变量(J2理论)有关：

(2)

采用与瞬时耗散现象相关的广义正交性假定，塑性流动可以表示为：

(3)

(4)

Chaboche根据上述屈服面运动规律，将随动硬化律中总背应力张量X进一步表示为多级背应力分量Xj的叠加。其中，基于五级背应力+线性项(N5L1)的模型近年来获得了较为广泛关注，其表达式可写成：

(5)

(6)

式(1)中各向同性硬化变量R主要用于描述材料的循环硬化/软化特性，其积分形式表示为：

R=Rs(1-e-bp)

(7)

式中：Rs表示硬化变量R能够达到的最大值；b表示其达到稳定的速度；p表示各向同性硬化律中的累积塑性应变，可通过下式估算：p=2Nεap。

将式(3)～(6)代入式(2)中，并进行积分，再叠加各项同性硬化部分(式(7))，则由式(1)可最终得到五级背应力+线性项的混合硬化本构模型(N5L1)的形式：

+vRs(1-e-bp)+vk

(8)

式中：X0和εp0分别表示背应力和塑性应变初始值；v=±1分别表示正、负塑性应变速率；Cj和γj表示材料常数，可由单调拉伸曲线或循环曲线得到。

2.2 基于混合硬化本构模型的轮盘榫槽疲劳寿命预测方法

基于局部应力/应变法，采用上述混合硬化本构模型预测轮盘榫槽疲劳寿命的步骤可归结如下：首先采用局部应力应变近似计算公式，并结合混合硬化本构模型，将转子轮盘作用载荷谱(具有恒定平均载荷，如图1所示)转化为榫槽缺口局部应力应变谱(出现了平均应力松弛)；然后选择修正平均应力的损伤模型计算每个加载循环的疲劳损伤；最终对所有加载循环的损伤进行累积，确定轮盘榫槽的疲劳寿命。

2.2.1榫槽齿根局部应力应变计算 Ye等[14-15]根据热力学原理建立的局部应力应变近似计算公式来确定榫槽缺口部位的局部应力应变，见式(9)：

(9)

式中：ΔS和Δe分别表示轮盘作用名义应力、应变范围；Δσ和Δε分别表示榫槽缺口局部应力、应变范围；ΔWq表示一个循环过程中的热量耗散。当材料满足幂硬化律时，上式也可进一步表示为：

(10)

式中：K′和n′为材料循环特性参数；局部应力范围Δσ=σmax-σmin，其中，σmax表示上一个加载循环结束时的最大局部应力，可通过上一个加载循环结束的局部塑性应变εp代入式(8)后确定；σmin表示上一个卸载循环结束时对应的最小局部应力，可从上一步计算结果中提取。将式(10)联合式(8)后则可得到基于混合硬化模型(N5L1)计算确定榫槽缺口局部的应力和应变。

2.2.2损伤计算与损伤累积 大量研究表明，SWT(Smith-Walker-Topper)模型[16]能够综合考虑应变幅与平均应力对疲劳损伤的影响，对于大多数材料与试验结果符合较好。因此，本研究采用SWT模型来计算轮盘榫槽的疲劳损伤，其表达式为：

(11)

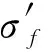
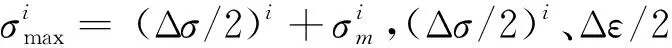
Di=1/Nfi

(12)

采用Miner线性准则对整个加载循环过程中榫槽齿根部位疲劳损伤进行累积，则有：

(13)

最终可确定考虑平均应力松弛的轮盘榫槽齿根的疲劳寿命(NfN)为：

NfN=N

(14)

采用Matlab软件对上述轮盘榫槽疲劳寿命预测过程进行编程，其计算流程可表示如图3。

图3 基于N5L1模型的榫槽构件疲劳寿命预测流程图Fig.3 Flow chart of the groove component life prediction based on N5L1 model

3 榫槽构件寿命预测及试验验证

3.1 榫槽材料低周疲劳特性参数的确定

为了确定榫槽材料的低周疲劳特性参数和混合硬化本构模型(式(8))中的材料参数，本文首先进行了榫槽材料的光滑试样室温拉伸实验及应变比R=0下的应变控制低周疲劳试验。表1列出了该榫槽材料的低

表1 榫槽材料低周疲劳特性参数Table 1 LCF mechanics properties of wheel groove material

周疲劳力学性能参数。

采用Kang等[17]提出的方法，结合单调拉伸曲线(需要去除各向同性硬化影响)则可确定式(8)中的随动硬化参数Cj和γj。

对于循环加载过程中背应力有显著变化的材料(如本文研究的轮盘材料)，在确定各向同性参数Rs和b时，忽略随动硬化(将背应力视为常数)会带来一定的误差，因此本研究引入摩擦应力：

σF=k+R=k+Rs(1-e-2bNΔεp)

(15)

图4为相应的拟合曲线。最终可确定混合硬化模型(式(8))中的各项参数如表2所示。

图4 σF-p曲线Fig.4 The curve of σF-p

表2 轮盘材料随动硬化及各向同性硬化参数Table 2 Kinematic hardening and isotropic hardening parameters of the rotor groove material

3.2 脉动加载下榫槽材料平均应力循环松弛行为模拟

使用上述混合硬化本构模型(N5L1)对脉动加载下榫槽材料的滞回环及平均应力松弛进行模拟。

图5给出了采用式(8)结合表1和表2中各参数模拟得到的两种应变幅下(较低应变幅0.6%(a)、较高应变幅1%(b))榫槽材料的的滞回环(最初和半寿命循环下)与试验结果比较。从图中可以看出，采用式(8)所示的混合硬化本构模型(N5L1)总体能够较好地模拟本文研究的榫槽材料在脉动加载下的循环应力应变响应。

图5 应变幅0.6%(a)和1%(b)下第一个循环及半寿命下的滞回环模拟Fig.5 Cyclic hysteresis loops under first cycle and half-life with strain amplitudes of 0.6%(a) and 1%(b)

图6是基于式(8)模拟获得的不同作用应变幅下平均应力松弛曲线与试验值的比较。从图中结果不难发现：在脉动作用应变幅下，榫槽材料出现了显著的平均应力松弛现象。在较高应变幅下(如1.0%)，平均应力在最初若干循环内即快速松弛到零；而在相对低的应变幅下(如0.6%)，平均应力相对松弛缓慢，并最终稳定在某一平均应力值。从图5中可进一步得出：混合硬化模型(N5L1)总体能够较好地模拟榫槽材料平均应力松弛行为。

图6 不同应变幅下的平均应力松弛模拟Fig.6 Simulations of the mean stress relaxation under different strain amplitudes

3.3 榫槽构件疲劳寿命预测及试验验证

为了验证本文建立的基于混合硬化本构模型的轮盘榫槽疲劳寿命预测方法的精度，对图7中某型汽轮机轮盘榫槽构件进行了疲劳寿命预测及试验验证。

图7 榫槽模拟件几何形状Fig.7 Geometry of the rotor groove component

由于图7中榫槽构件存在多个缺口，而其疲劳失效通常是由应力集中最严重的缺口所决定。因此，本文首先采用有限元法计算了榫槽构件各缺口的应力集中系数(Kt)，结果见表3所示。

从表3可以得出，榫槽构件的齿根A存在最大应力集中系数，是榫槽构件的最危险部位。因此，本研究对榫槽构件的疲劳寿命预测主要针对该缺口进行，其计算过程采用图2所示的流程，并结合表1和2中榫槽材料的低周疲劳特性参数。

表3 榫槽构件各缺口理论应力集中系数Table 3 Theoretical stress concentration coefficient of each notch of the rotor groove component

为了验证本文榫槽构件疲劳寿命预测方法的精度，对图6的榫槽构件参照相关标准[18]进行疲劳实验，试验在MTS-810电液伺服疲劳试验机上进行，采用应力比R=0的轴向载荷控制，正弦波加载。为了确保实际载荷响应与控制载荷一致，试验频率在0.0333～0.1 Hz范围内调整。试验过程中采用100倍长距离显微测试系统(见图8)对榫槽缺口部位的裂纹萌生与扩展进行观察，并将出现0.5mm左右的裂纹对应的循环周次作为榫槽构件的裂纹萌生寿命。实验中也发现，榫槽构件的裂纹通常在A缺口最先萌生，这与该缺口应力集中最严重部位(见表3)一致。

图8 榫槽构件低周疲劳试验现场(a)及裂纹观察(b)Fig.8 (a)LCF test site；(b) observation of crack

表4给出了榫槽构件的疲劳寿命预测值及试验结果。这里作为比较，也给出了基于平均应力松弛经验公式(Landgraf[2])的疲劳寿命预测结果。图9则是上述预测寿命与实验结果的比较。

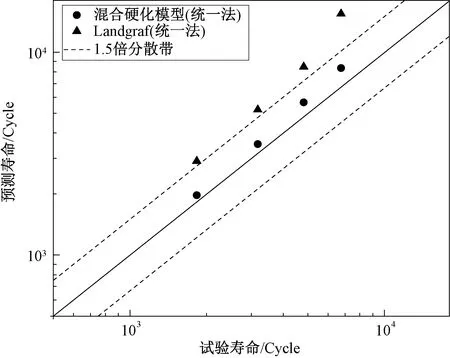
图9 榫槽构件预测寿命与试验寿命的比较Fig.9 Comparison of the predicted life and measured life of the rotor groove components

表4 轮盘榫槽构件寿命预测结果及试验寿命值Table 4 Predicted and measured fatigue life of the rotor groove components

从表4中可以看出，相比于Landgraf平均应力松弛经验公式，本研究基于混合硬化模型(N5L1)的疲劳寿命预测精度有了显著提高。前者与试验寿命误差约在50%～130%之间，而后者预测寿命与试验值误差总体控制在7%～25%之间。由此可以得出，本研究基于混合硬化模型(N5L1)的寿命预测方法可实现对榫槽构件疲劳寿命更为准确的预测。由于混合硬化本构模型可直接模拟疲劳过程中的平均应力松弛行为，而无需专门开展非零平均应力下的疲劳试验，这大大方便于实际应用，因此更值得工程上重视。

1．在R=0的应变控制疲劳试验中，轮盘榫槽材料的平均应力随着循环出现明显的松弛现象。本文采用混合硬化本构模型(N5L1)能够较好地模拟榫槽材料的平均应力循环松弛行为。

2．基于局部应变法，采用混合硬化本构模型(N5L1)，并结合近似公式计算榫槽缺口局部应力应变历程，采用SWT模型计算疲劳损伤与线性损伤累积，从而建立了一种预测轮盘榫槽构件疲劳寿命预测的新方法。

3．本研究建立的基于混合硬化本构模型的疲劳寿命预测方法较采用平均应力松弛经验公式(Landgraf)的寿命预测方法具有更高的预测精度，通过对某榫槽构件进行寿命预测并与试验结果相比较，两者相对误差总体在1.5倍分散带以内。因此，该方法值得在汽轮机轮盘榫槽抗疲劳设计中重视。