基于阵列涡流技术的管道变形检测数值分析*
2022-02-28辛佳兴陈金忠李晓龙朱宏武王长新
辛佳兴 陈金忠 李晓龙 朱宏武 王长新
(1.中国石油大学(北京)机械与储运工程学院 2.中国特种设备检测研究院压力管道部)
0 引 言
近年来, 我国油气管道建设事业迅速发展,相关资料[1]表明,截止到2019年底,我国长输管道总里程达16.9×104km,到2025年,管网规模将达到24.0×104km。与公路、铁路和海洋等运输方式相比,管道运输[2]是相对可靠且高效的能源运输方式。管道网络点多、线长、运行环境特殊[3],安装环境复杂,应力集中[4]、地壳运动以及机械损伤[5]等会均会导致管道出现不同程度的变形,造成管道运输速率下降和局部强度降低。及时发现管道变形缺陷[6]并排除安全隐患[7],对保证油气资源正常运输有重大意义。
相对于传统的油气管道缺陷检测技术,涡流检测技术有着快速、高精度、非接触的优点,近年来国内外学者对此进行了大量研究[8-10]。PIAO G.Y.等[11]利用涡流检测方法,研制了涡流检测探头并进行了管道内检测牵拉试验,实现了被测管道内外壁缺陷识别和定量分析;汤祺[12]利用分时激励阵列脉冲涡流位移检测方法,对油管直线度和椭圆度进行了定量检测,并给出了油管椭圆度和直线度测量算法;王宝超等[13]基于涡流传感技术,研制了非接触式管道变形内检测设备,并进行了管道牵拉试验,验证了该设备管道变形检测的有效性;刘锐[14]依据涡流检测原理,研制了涡流管道膨胀检测传感器,并通过试验验证了该传感器可实现管道变形的动态与多通道测量;WANG Z.W.等[15]从磁畴的微观水平解释了铁磁性材料的涡流检测的机理,并系统研究了缺陷尺寸与检测信号峰值之间的关系。
在上述研究的基础上,本文对阵列涡流管道变形检测技术进行理论分析,从磁畴的微观水平上解释了涡流信号的变化机理,提出变形检测探头的不同布置方案,利用Maxwell有限元分析软件进行数值模拟,研究了阵列涡流传感器的不同布置方案对磁敏感元件输出信号的影响,并推导了传感器输出信号变化量ΔV与管道变形量Δd之间的数学模型,所得结论可为阵列涡流管道变形内检测器的研制提供技术支撑。
1 管道涡流变形检测理论
1.1 涡流变形检测理论
电磁场理论核心是麦克斯韦方程组,从本质上说,阵列涡流管道变形检测问题就是麦克斯韦方程组的求解及验证的过程,方程组的微分形式如下:
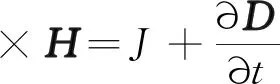
(1)
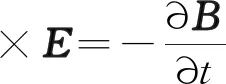
(2)
∇·D=ρ
(3)
∇·B=0
(4)
式中:H为磁场强度,A/m;J为电流密度,A/m2;D为电位移矢量,C/m2;E为电场强度,V/m;B为磁感应强度,T;ρ为体积载荷密度,C/m3。
涡流检测原理如图1所示。当激励线圈通入交变电压信号时,根据安培定律,在空间内会产生交变的一次磁场H1,假设该磁场在空间中一点处的磁感应强度为B1,B1的方向可以通过右手螺旋定则确定;当交变的一次磁场H1作用于被测试件时,由于试件表面的磁通量发生变化,由法拉第电磁感应定律可知,试件表面将产生感应电动势,从而产生涡电流,变化的涡流将在空间内产生一个变化的二次涡流磁场H3,其磁感应强度为B3。
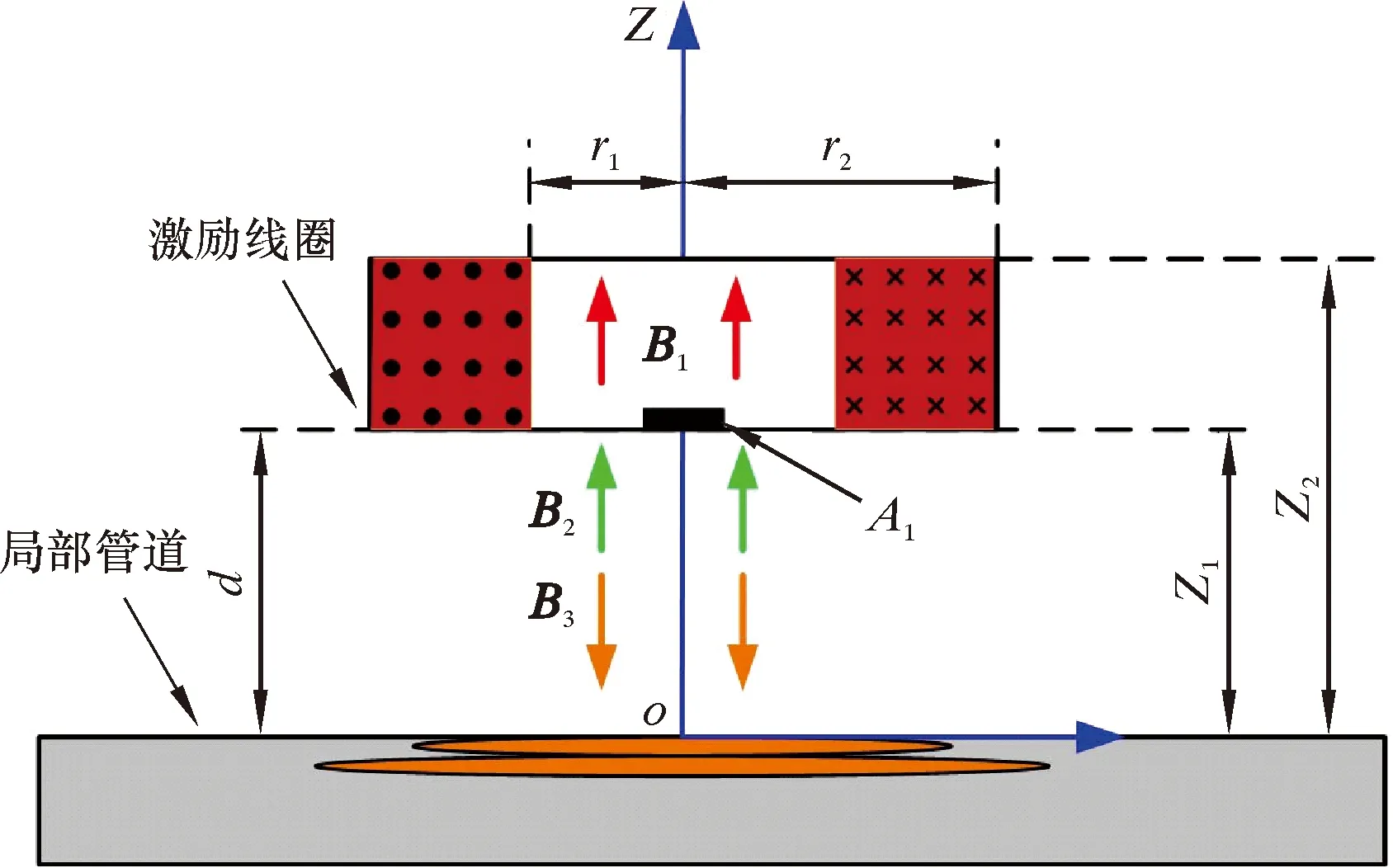
图1 涡流检测原理
铁磁性材料在弱磁场范围内的磁化过程主要是畴壁的位移过程,即沿着外磁场方向磁畴增大,与外磁场方向相反的磁畴缩小[16]。X52、X60和X70等铁磁性管材具有高磁导率的特点,在一次磁场H1的作用下,管道局部被磁化,内部磁畴向着磁场H1方向发生旋转,因此产生磁化磁场H2,其磁感应强度为B2。外磁场作用下管道磁畴偏转示意图如图2所示。图2a中线圈与被测管道间的距离d很小,因此被磁化的局部管道处一次磁场H1值较大,激发出较强的磁化磁场H2,由于与被测管道处的一次磁场与线圈间距离d成反比,所以随着d值的增加,被磁化部分磁畴偏转所激发出的磁场B2呈现出由图2a到图2d依次减小的变化规律。
磁性芯片在空间中某一点处获取的复合磁感应强度B是B1、B2与B3的矢量和,B值可以由式(5)确定:
B=B1+B2+B3
(5)
其中,线圈轴线上A1点的磁感应强度B1可以由毕奥萨伐尔定律定量确定:
(6)
式中:n为线圈匝数,I为线圈中通过的实际电流,μ0为真空中的磁导率,Z2与Z1的差值表示线圈高度,r1为线圈内径。
管道由于磁化作用激发出磁场H2,在A1点处的磁感应强度B2可以通过式(7)确定:
B2=μ0χ(H1)H1(Z1)
(7)
式中:χ为磁化系数,是关于激励线圈产生磁场H1的函数;H1为被测试件所处位置Z1处激励线圈所产生磁场强度,其大小与线圈和被测试件之间距离d值有关。
管道内表面涡流场激发出磁场H3,在A1点处的磁感应强度B3可以通过式(8)确定:
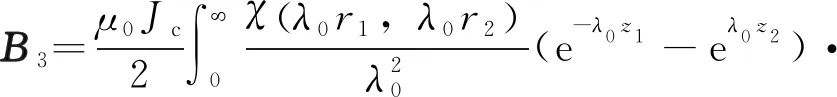
(8)
式中:Jc为等效的理想单匝线圈电流密度,J1(λ0)为第一类一阶Bessel函数,λ0为积分变量,R(λ0)是与被测材料电导率和磁导率相关的物理量。
综上所述,对于同一涡流传感器,固定被测管材的磁导率、电导率及激励参数,复合磁场的磁感应强度B仅是激励线圈和管道内表面间距离d的函数,因此可通过提取复合磁场的磁感应强度B实现量化管道形变量Δd的目标。
1.2 涡流变形检测探头布置方案
管道涡流变形内检测器三维模型如图3所示,主要包括里程轮、检测器骨架、检测探头、皮碗和防撞头等。

1—里程轮;2—皮碗;3—防撞头;4—检测探头;5—检测器骨架。
内检测器上的检测探头通常采取阵列方式沿管道周向布置。检测探头由涡流变形检测模块组成,单一的检测模块包括检测线圈、磁性芯片及电路系统,其中磁性芯片是将空间内一点处的磁场强度转化为模拟电压信号的元件。对于阵列式管道变形检测传感器,其阵列密度越大,对管道周向检测分辨率越高,变形检测效果越好。但提高传感器的阵列密度,则需减小阵列传感器的间距,传感器单元的间距越小,其检测模块间的相互干扰变大,对涡流变形检测探头输出信号的影响也越大。
涡流变形检测探头布置方案大体上可分为3种,如图4所示。方案1:单个检测探头由1个涡流变形检测模块封装而成,相邻线圈间距足够大,可认为彼此间的电磁干扰很小;方案2:单个涡流检测探头由2个涡流变形检测模块封装而成,单一的涡流变形检测模块只受邻近检测模块的电磁干扰;方案3:单个涡流检测探头包含3个涡流变形检测模块,并且涡流检测探头等间距布置,可认为相邻单一变形检测模块受邻近2个检测模块的电磁干扰。

图4 涡流变形检测探头布置方案
在管道变形缺陷检测的工程中,变形内检测器在管道内介质的推动下,沿着管道轴向方向以速度v运动。管道变形内检测器变形检测示意图如图5所示。当内检测器所处位置的局部管道未发生形变,则变形检测探头与管道表面的距离d为一定值,其输出信号为V;当内检测器通过变形区域时,变形检测探头与局部被检测管道的相对距离改变为dx,其输出信号为Vx,此时管道的变形量Δd=d-dx,变形检测探头输出信号的变化量ΔV=V-Vx,变形检测探头内磁性芯片感应到的磁场强度变化量可以由式(9)求得:
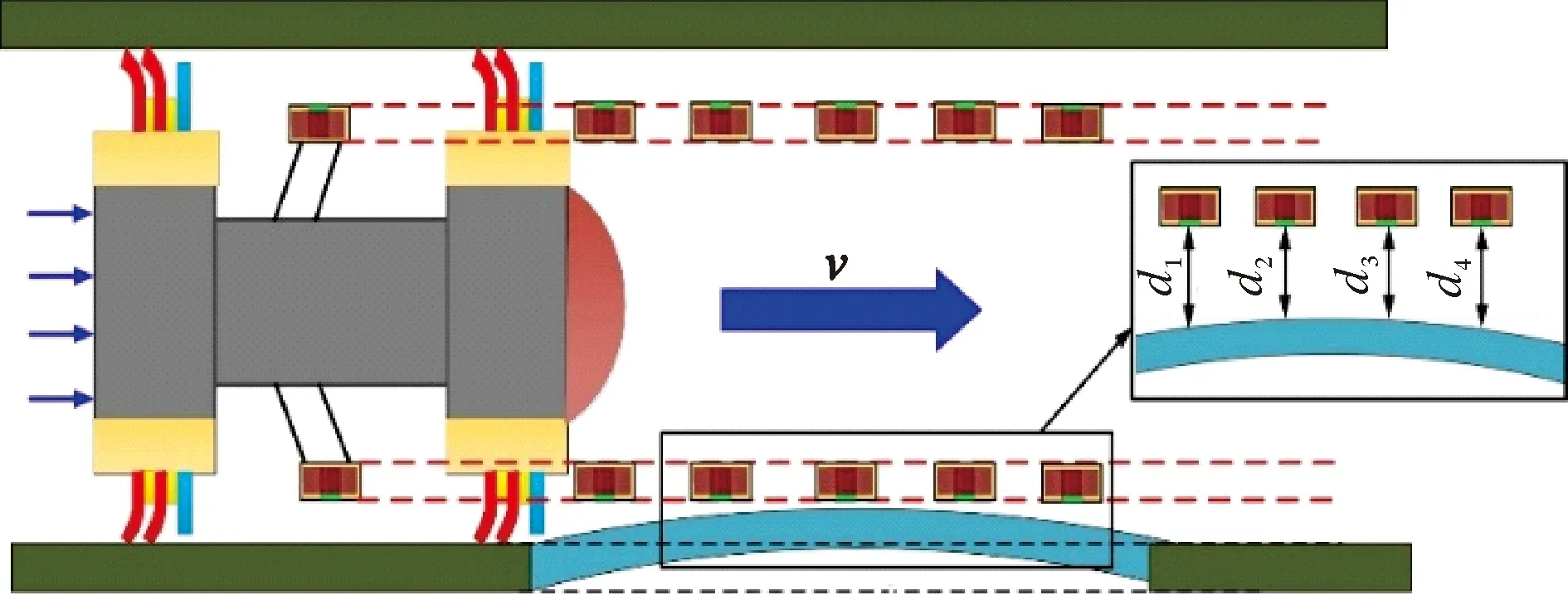
图5 管道内检测器检测管道变形示意图
(9)
式中:ΔV表示管道未变形处检测探头输出电压信号与管道变形时检测探头输出电压信号的差值,k表示与磁性芯片灵敏度及电路放大倍数相关的常量。
下文将通过数值模拟的方法来探究管道涡流变形检测探头在不同布置方案下ΔB随Δd的变化规律。
2 数值模拟
由文献[17]可知,当管道曲率相对于传感器尺寸较小时,利用平面代替管道弧面进行仿真分析对结果影响较小。因此,利用Maxwell有限元分析软件建立简化的三维阵列涡流管道变形检测模型,模型主要包括激励线圈、求解点A1(磁性元件位置)、被测试件和空气域。
激励线圈内径为5 mm,外径为13 mm,高度为5 mm,匝数为90。激励电压信号幅值为1.5 V,频率为500 Hz。待检测平板材料设置为低碳钢steel_1008,被测试件(长×宽×高)为100 mm×50 mm×5 mm。
2.1 模型建立
涡流变形检测模块如图6所示。磁性芯片位于激励线圈轴向与下边沿交点A1位置处。受实际应用中探头封装和外壳等尺寸限制,激励线圈不可能无限靠近被测试件,因此设置激励线圈与被测试件的距离d值由1 mm增加到11 mm,步进1 mm。
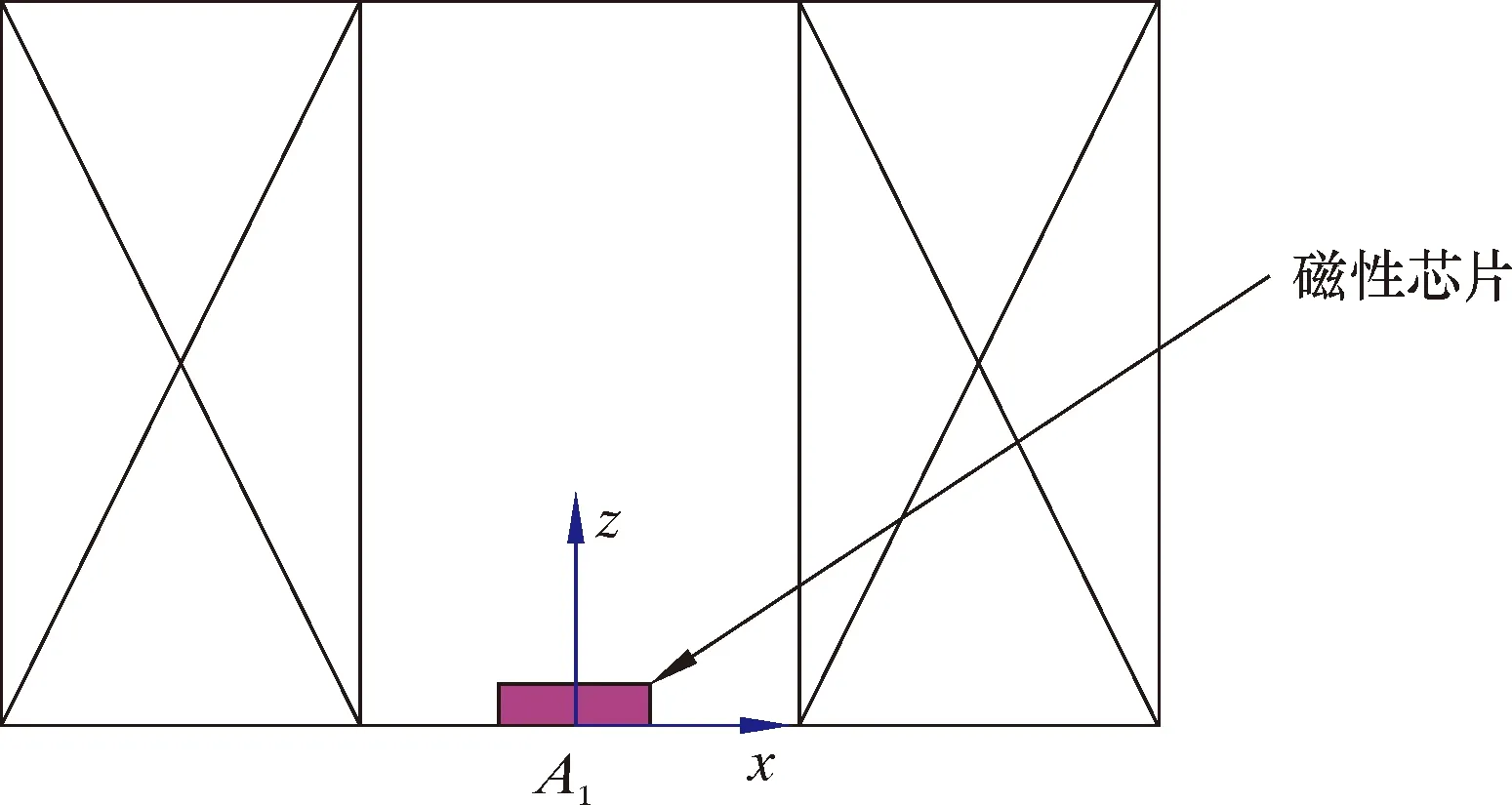
图6 涡流变形检测模块
为研究不同传感器布置方案下A1点磁感应强度峰值随d值的变化规律,建立三种布置方案的三维仿真模型。图7为单涡流变形检测模块三维模型。图8为双涡流变形检测模块三维模型。图9为阵列涡流变形检测模块三维模型。
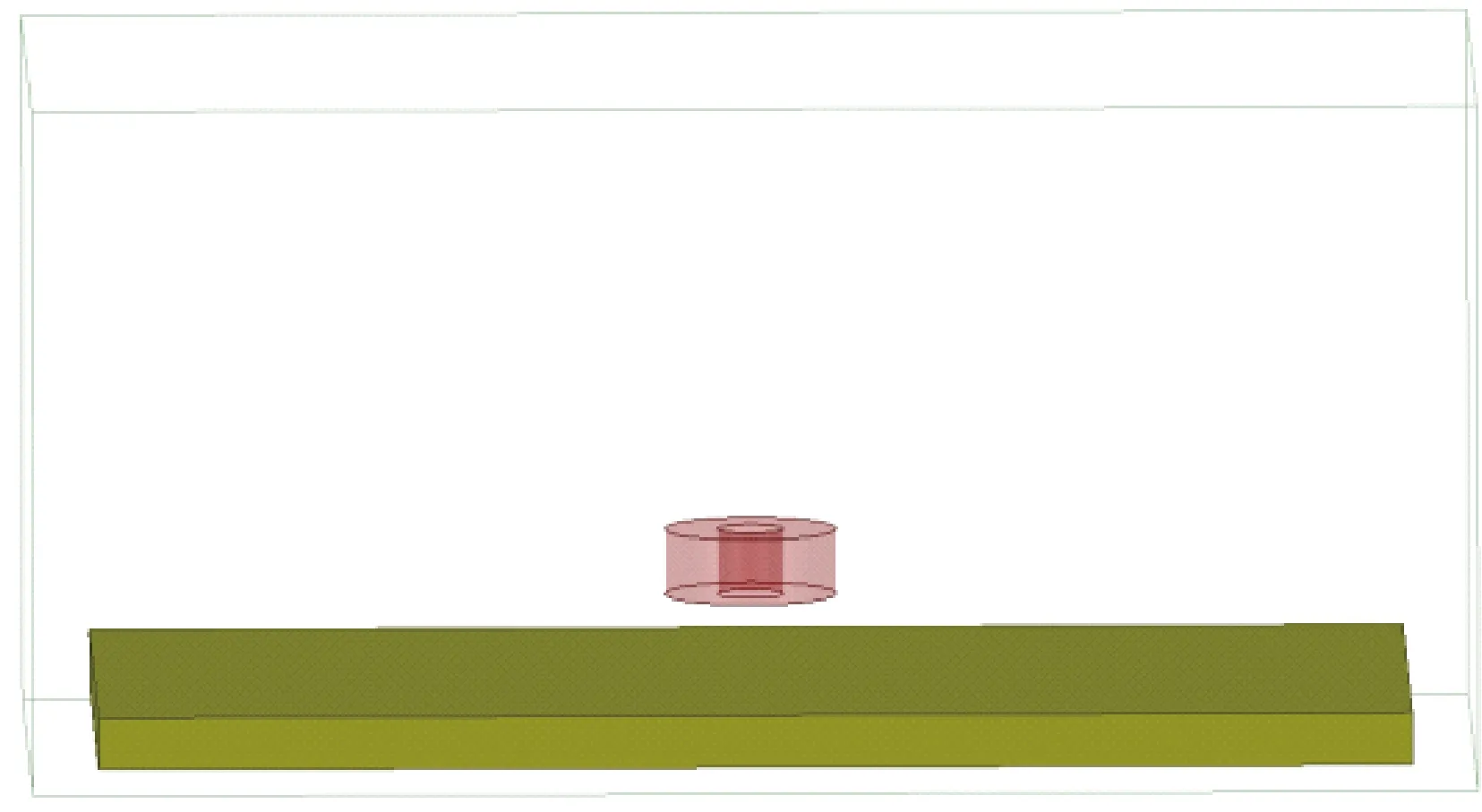
图7 单涡流变形检测模块三维模型

图8 双涡流变形检测模块三维模型
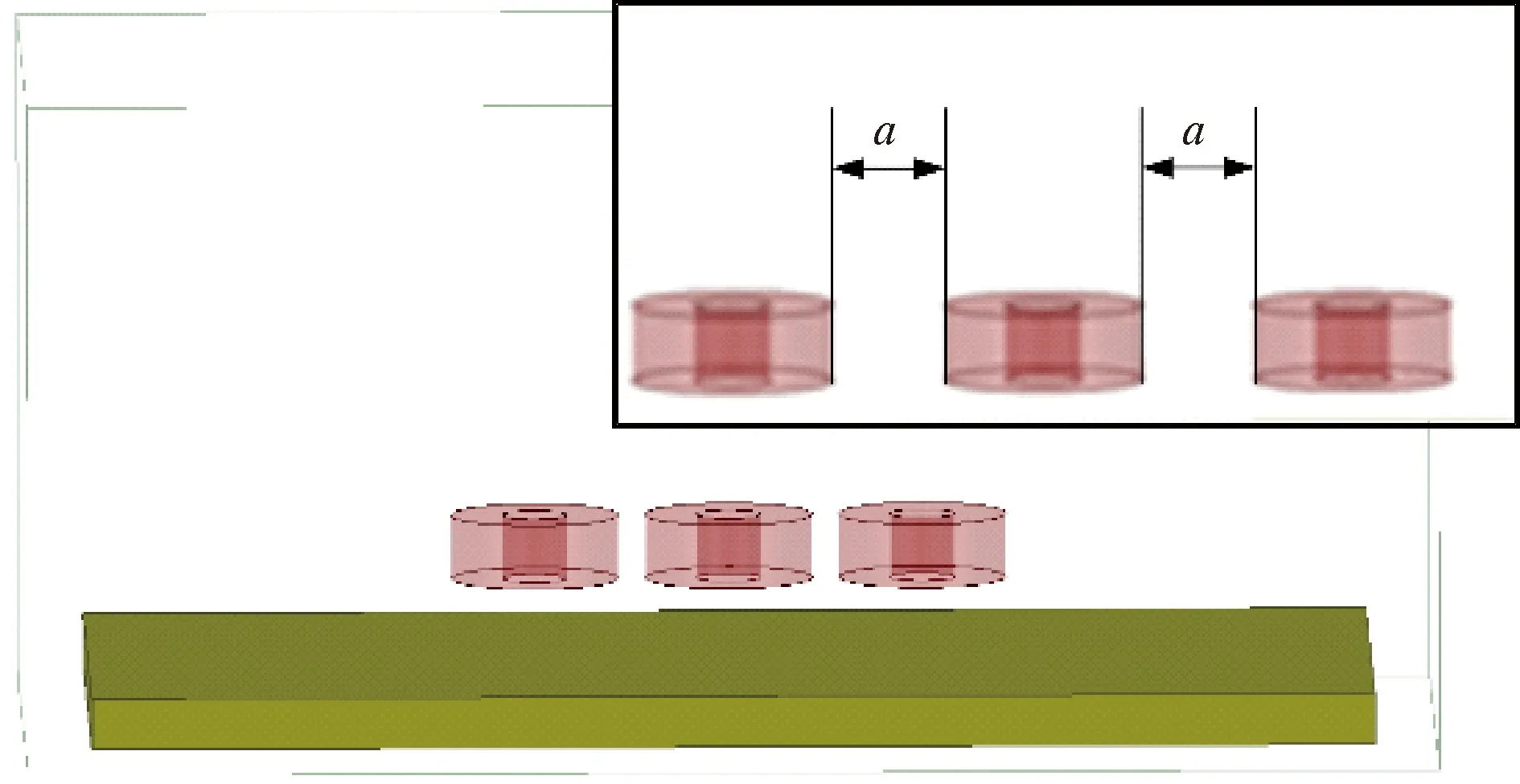
图9 阵列涡流变形检测模块三维模型
2.2 仿真结果
假设管道未发生变形时,涡流变形检测探头与管道内壁的距离d值最大为11 mm。采取方案1布置时,点A1处z方向磁感应强度分量ΔBz的输出结果如图10所示。由图10可知,不同探头提离高度d下,各输出信号的变化趋势基本保持一致,并且在同一d值下,在时域上一周期内的0.7 ms时刻A1点磁感应强度达到峰值。
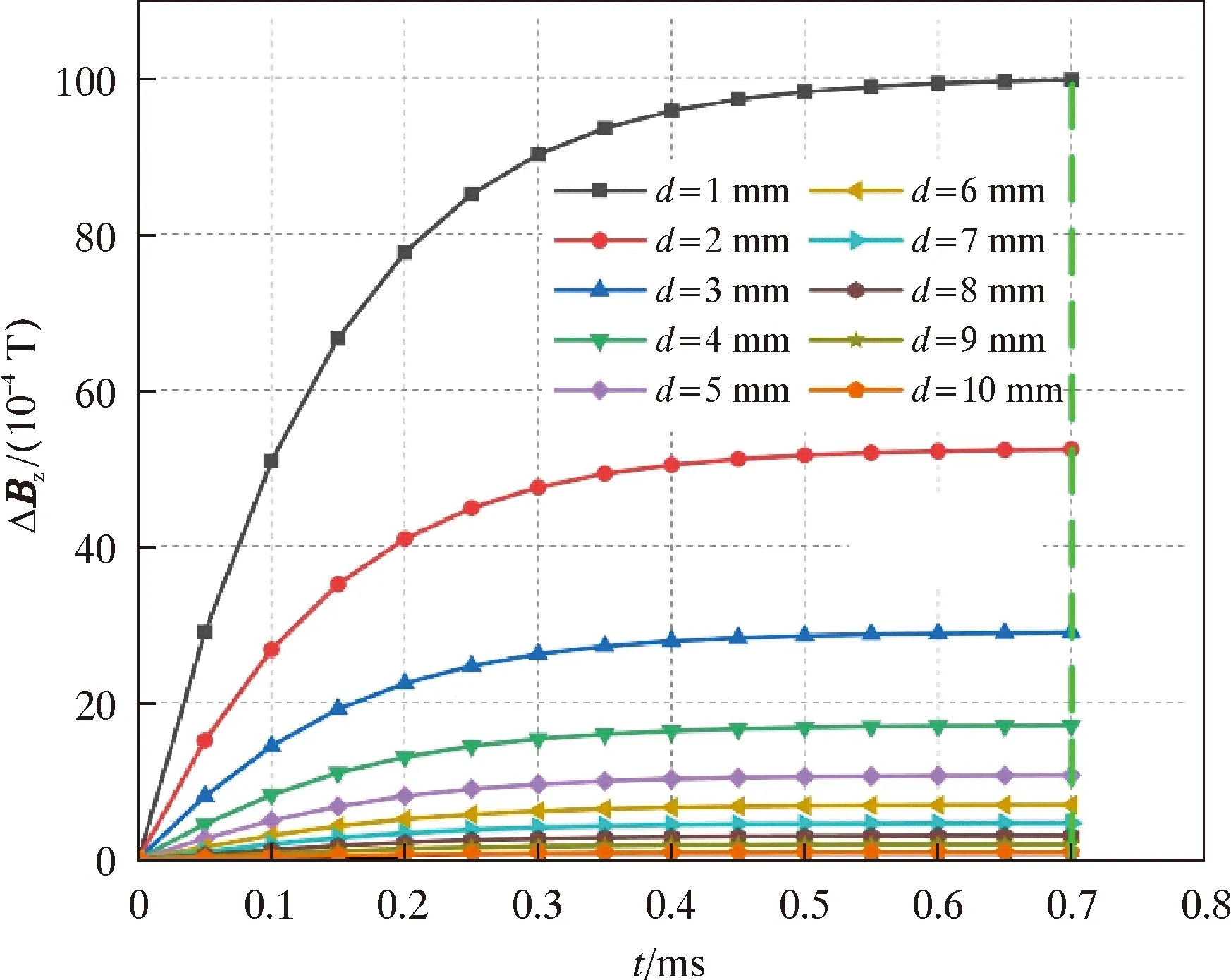
图10 单线圈布置A1点ΔBz的变化曲线
当采取方案2布置时,a=0时相邻线圈间的电磁感应最大,对A1点磁场强度的电磁干扰最大。仿真模型中设置a=0.1 mm,绘制A1点磁感应强度差值分量ΔBz随d值的变化曲线,如图11所示。
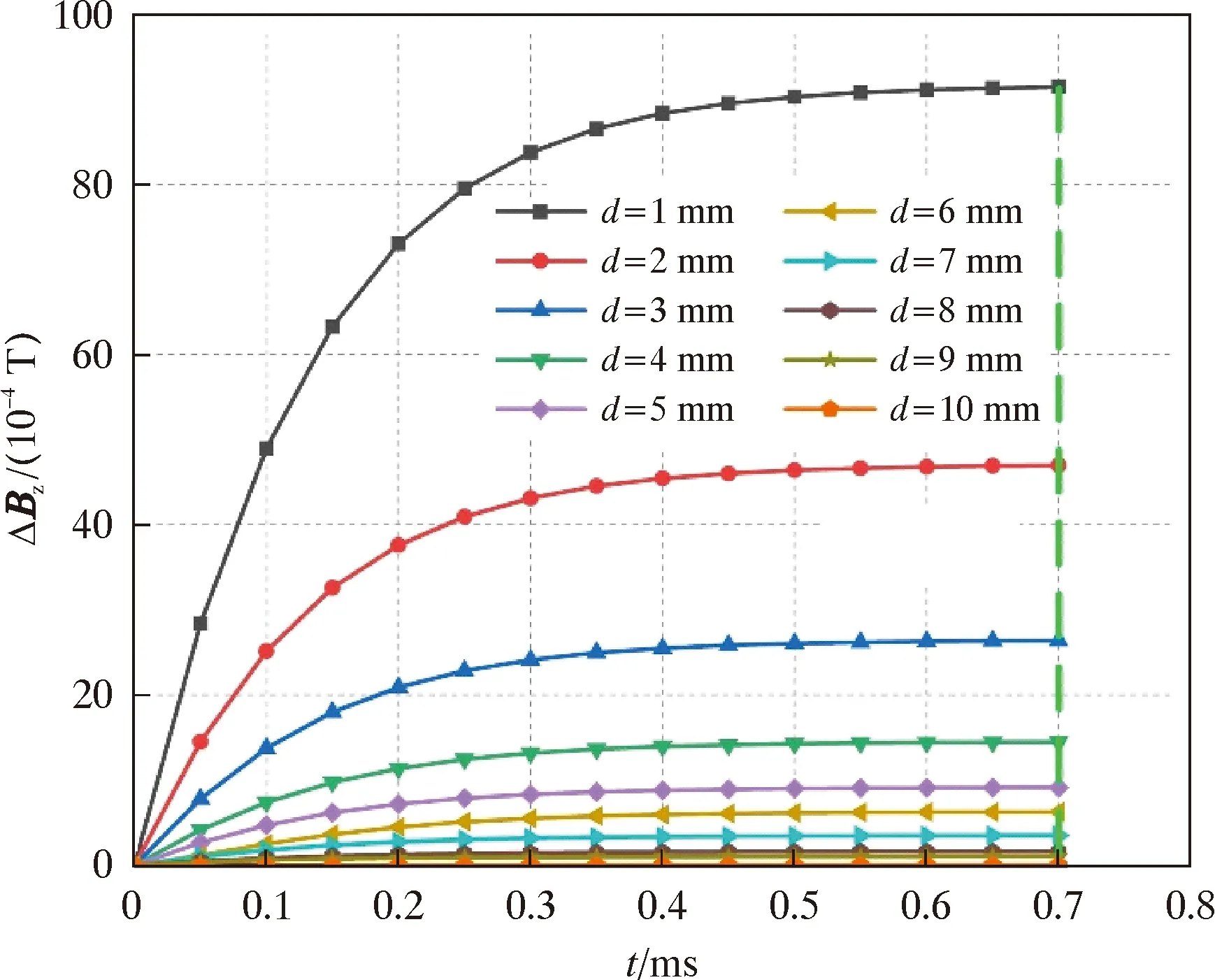
图11 双线圈布置A1点ΔBz的变化曲线
当传感器采取方案3布置时,线圈间距a=0时,中间线圈内的A1点受相邻线圈电磁干扰的程度最大。因此只分析中间线圈A1点磁感应强度的变化规律,绘制A1点磁感应强度差值分量ΔBz随d值的变化曲线,如图12所示。
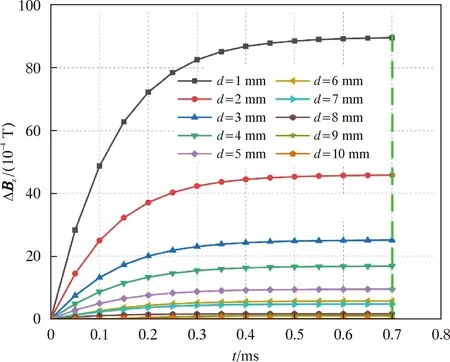
图12 三线圈布置A1点ΔBz的变化曲线
3 结果及讨论
磁感应强度峰值信号包含被测试件丰富的缺陷信息,因此提取3种布置方案下A1点Bz峰值,绘制Bz峰值随d值的变化曲线,如图13所示。
图13中3条曲线变化趋势基本相同,Bz与d呈现负相关的非线性变化规律,并且存在 “急促-缓慢-稳定”的3个变化阶段。

图13 Bz峰值随d值的变化曲线
在1~11 mm范围内,3条曲线的磁感应强度变化分别为L1、L2和L3(L1=99.70×10-4T、L2=91.41×10-4T、L3=89.58×10-4T),其平均变化量分别为S1、S2和S3(S1=9.970×10-4T/mm、S2=9.141×10-4T/mm、S3=8.958×10-4T/mm)。当d值在1~5 mm范围内变化时,为曲线的“急促”变化阶段,3种布置方案的磁感应强度变化量均大于5×10-4T/mm,平均磁感应强度变化量分别为22.26×10-4、20.57×10-4和20.02×10-4T/mm;当d值在5~8 mm范围内变化时,为曲线的“缓慢”变化阶段,3种布置方案的磁感应强度变化量均大于1.5×10-4T/mm,其平均磁感应强度变化量分别为2.57×10-4、1.88×10-4和1.95×10-4T/mm;当d值在8~11 mm范围内变化时,为曲线的“稳定”变化阶段,3种布置方案的磁感应强度变化量小于1×10-4T/m。实际检测中存在噪声,认为涡流传感器在与管道内表面距离d大于8 mm时,对变形检测能力较低。
出现上述变化的原因是管道作为高磁导率的铁磁性材料,受激励线圈的磁化作用明显,管道磁畴偏转产生的B2比涡流场产生的B3更强,因此Bz与d表现出负相关。具体来说,当d值较小时,在B1的作用下,局部变形管道的磁畴向着B1方向偏转程度大,在空间A1点激发出较强B2;随着d值增加,B1对局部变形管道磁化程度降低,磁畴偏转激发出的B2减小,因此空间中A1点的复合磁场强度B减小。
对比3条曲线,可以发现检测探头与管道内壁间距离d值相同时,采用方案一涡流变形检测模块单独布置时Bz值最大。相邻线圈激发出的外加磁场B4方向与中间线圈激发出磁场B1的方向相反,导致传感器阵列布置时,A1点在同一d值下的Bz信号减小,因此同一d值下,单一涡流变形检测模块布置时Bz值最大。平面磁场分布矢量图如图14所示。
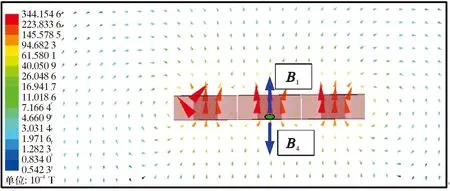
图14 平面磁场分布矢量图
差分信号ΔBz反映管道形变量Δd对于传感器输出信号影响的差异程度。ΔBz峰值随管道变形量Δd值的变化曲线如图15所示。
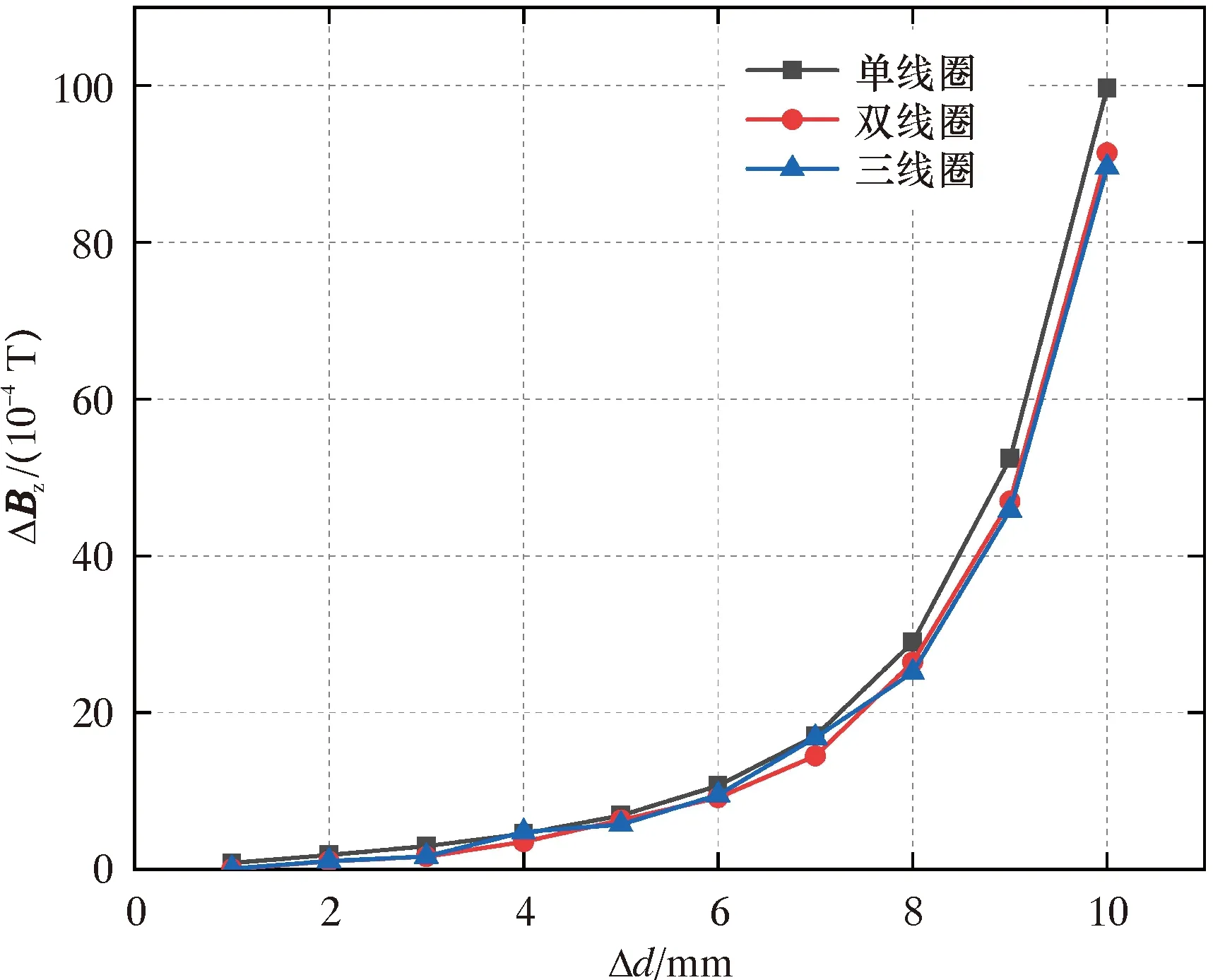
图15 ΔBz峰值随Δd值的变化曲线
ΔBz峰值随管道变形量Δd的拟合方程为:
ΔBz=C1Δd+C2(Δd)2+C3(Δd)3+C4(Δd)4
(10)
式(10)中的C1、C2、C3和C4参量取值如表1所示。
在三种布置方案下,ΔBz与Δd均呈四次多项式递增的变化规律,并且三条曲线的相关性系数R2均大于0.99,这表明曲线拟合情况良好。
由式(9)与式(10)联立,可得传感器输出信号变化量ΔV与管道变形量Δd之间的关系式:
ΔV=k[C1Δd+C2(Δd)2+C3(Δd)3+C4(Δd)4]
(11)
在管道内检测工程应用中,可以提取阵列涡流检测模块的电压信号差值的峰值ΔV作为特征量,据此对管道不同位置处的变形量Δd进行定量计算。
4 结 论
(1)对于油气管道等铁磁性材料,采用电涡流法检测管道变形时,铁磁性材料因磁畴磁化产生的感应磁场强度大于感应涡流场所产生的磁场强度。
(2)对于电涡流管道变形检测技术,当探头与管道内表面间的距离d值大于8 mm时,磁感应强度平均变化量小于1×10-4T/mm,考虑实际检测中存在噪声,管道变形量检测可靠性及精度降低,因此应控制d值小于8 mm。
(3)阵列涡流检测传感器输出信号变化量ΔV与管道变形量Δd呈四次多项式递增的变化规律;对比单线圈涡流传感器,阵列涡流传感器在磁场互感影响下磁感应强度灵敏度至多下降10%。
(4)在管道涡流变形内检测器研发过程中,为提高涡流变形检测探头对管道形变Δd检测的灵敏程度,应适当增加相邻检测模块的间距。
