液控单向阀瞬态开启过程流固耦合特性研究*
2022-02-28谢小路何东升张林锋李川王波代辉
谢小路 何东升 张林锋 李川 王波 代辉
(西南石油大学机电工程学院)
0 引 言
液压解码器是ICV的核心液控系统,而液控单向阀作为液压解码器的核心元件,其动态响应和可靠性直接影响整个系统的工作性能。
液控单向阀在工作过程中由于流场不稳定导致的振动、噪声等问题属于流固耦合范畴,国内外文献使用CFD和试验的方法建立了常规单向阀的分析模型,对其稳定性和非线性运动特性进了研究,但针对液控单向阀的研究较少。
文献[1-2]采用Fluent建立了气液单向球阀的CFD模型,分析了阀芯材质、弹簧刚度、含气体积分数和入口流量等对单向球阀瞬态开启稳定性的影响。文献[3]采用动网格方法分析了弹簧刚度对锥阀的瞬态液动力性能的影响。文献[4-5]则基于Fluent动网格技术建立了容积泵内单向阀流固耦合数值模型,使用用户自定义函数(UDF)控制阀芯的位移,研究了单向阀在开启过程中的瞬态响应,获得了与试验相近的损耗系数,还对比了时间步长、湍流模型及求解模型等仿真参数对数值结果的影响,指出使用隐式求解方案优于显示方案。文献[6]采用CFD技术研究了截止阀开启与关闭过程中阀体内部的速度、压力分布以及压力损失等情况,分析了流体通过阀道时产生的漩涡、水锤和死水区等水流情况,指出阀的开启和闭合会导致压力大幅度波动。文献[7]基于CFD软件和试验研究了飞机燃油系统用某单向阀开启过程,指出阀芯的最大开度位置与弹簧刚度、阀芯形状和内部流道有着密切关系。文献[8]利用Fluent软件的6DOF模块建立了插装阀开启过程中的非定常流场模型,数值模拟计算出的阀芯位移、控制腔压力和稳态液动力与理论公式计算值相符,指出与常规方法相比,CFD方法的结果与阀芯实际运动更加接近。文献[9]通过设计试验研究了锥阀的振动和噪声现象,指出瞬态液动力导致了锥阀的规律周期振动现象。文献[10-11]则基于三维流固耦合有限元动力学仿真分析和直接耦合算法,建立了一种车用锥形节流阀由关闭至开启而后又关闭全过程的数值分析模型,研究结果表明,影响阀芯振动频率较为显著的因素是阀芯质量和油液体积模量,阀芯和阀座之间的接触碰撞会提高其振动频率。
以上基于Fluent动网格的方式实现流固耦合分析的文献,其使用的UDF程序无法实现对阀芯的振动分析。而本文采用Fluent 6DOF模型和网格重构理论,考虑了阀芯至极限位置后的振动情况,编译了一套新的UDF,建立了单向阀受到微型液缸推杆推力作用下的瞬态开启过程的非稳态强耦合动力学响应分析模型。
1 结构模型及工作原理
1.1 结构模型
解码器实物三维透视图如图1所示。解码器内部集成了多个微型液控单向阀(以下简称单向阀)组件。压力损失小和响应迅速是实现地面远程控制命令的基本保证之一,因此有必要对单向阀瞬态开启过程进行深入分析。
单向阀结构如图2所示。
1.2 工作原理
单向阀的工作原理为:在初始状态下,常闭单向阀受到进出口压差的影响,单向阀内的小球堵住了内部流道,液压油无法联通,当连通微型液缸的液压油先推动其内部活塞向左运动,活塞推杆运动到和单向阀内部阀芯小球接触,由于活塞对小球的推力Fp大于流体对小球的阻力Fv与弹簧弹力Fs之和,此时小球在活塞推力作用下逐渐开启,阀芯运动方向与流体流动方向相反,阀芯的运动受到活塞推力和液压油压力的共同影响。
2 数值模型
为研究阀芯受力运动情况,采用瞬态方法进行计算,对流体区域采用有限体积法,采用Fluent动网格技术并编译一套新的UDF程序来实现开启瞬态过程的数值计算。
2.1 控制方程
数值计算选用了Fluent软件中的RNGk-ε湍流模型,使用基于压力-速度耦合的Simple算法,动量方程中的雷诺应力张量使用涡黏度模型[4-5,12]:
(1)
(2)
式中:k为湍流动能,ui为速度分量,μ为运动黏度,ε为耗散率。
使用具有标准壁面函数(standard wall function)的RNGk-ε湍流模型,此方程引入了对湍动黏性系数的修正方程,在模拟流动分离、强旋流和弯曲壁面流动等问题时更接近实际流动状态。湍流动能k以及其耗散率ε来自以下传输方程[12-13]:

(3)
(4)
(5)

2.2 网格参数
本文采用Fluent Meshing进行网格划分。为了降低计算时间成本和动网格参数的需要,将计算域分成3个混合域(见图3),各域之间用Interface连接,且只在“中”部非结构域内部进行网格更新,其网格类型为四面体,“上”和“下”两个域采用多面体-六面体(Poly-Hexcore)网格。整个模型共535 433个节点(nodes)和1 258 055个单元(elements)。网格质量在0.38以上,满足Fluent求解计算要求。
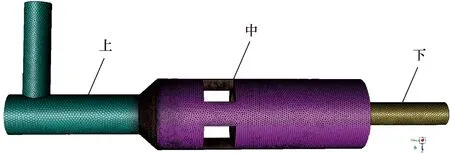
图3 单向阀网格模型
2.3 使用Fluent UDF控制阀芯运动
在活塞推动阀芯运动之前,阀芯受到的预紧力FOFF由液压油对其的液动力Fv和弹簧预紧力F0共同组成。阀芯的运动由合力决定,其受力简图如图4所示。图4中Fp为阀芯推杆推力,Fs为弹簧力。

图4 阀芯运动受力简图
由牛顿第二定律推导出如下二阶常微分方程,用于模拟阀芯的运动[14-15]。
(6)

对式(6)左侧进行简化,可以得到运动部件(阀芯)的加速度表达式[16]:
(7)

(8)
引入阀芯的位移yt为自变量,弹簧力的表达式为:
(9)
式(9)中K是弹簧的弹性系数,于是可以得到新的离散方程[17]:
(10)
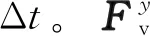
由于ANSYS Fluent无法直接读取执行等式(9),所以需要使用UDF编译模块对等式进行程序化处理。式中的参数有阀芯质量为0.006 08 kg,弹簧弹性系数K为2 600 N/m,弹簧预紧力F0为5.2 N,Fp取769 N,时间增量步为0.000 01 s。
2.4 动网格(Dynamics Mesh)更新技术
本文使用弹簧近似光顺(spring-based smoothing)和局部网格重划法(local remeshing),结合两种方法相互作用生成动态网格。使用编译UDF程序控制阀芯时,由于计算域随着阀芯瞬态位置的变化而变化,为避免出现负体积网格,需要在下一次迭代计算前对网格做更新处理。
2.5 边界条件设置
使用Fluent进行数值计算,阀内流体为32#液压油,密度为850 kg/m3,运动黏度为0.001 18 Pa·s,入口和出口边界分别设定为压力入口和压力出口,进口压力5 MPa,流速0.5 m/s,出口压力为4.5 MPa,为了增强动量的收敛性,将动量欠松弛因子设为0.4[16],其他参数设定为默认标准。
3 结果分析
3.1 流体-结构相互作用对阀芯运动特性的影响
使用UDF程序提取并记录流体对阀芯的合作用力,流体作用力直接影响阀芯的运动,是造成阀工作不稳定的重要因素之一。
图5为阀芯受到的瞬态液动力Ff随时间的变化规律。由图5可知:在阀芯移动前,流体作用力维持在30.6 N左右,和推力Fp大小无关;阀芯移动瞬间,Ff有小幅增加的趋势,并在开启过程中基本保持不变;当阀芯位移至最大时受微型液缸推力影响,阀芯运动速度为0,此时阀芯周围流场极不稳定,瞬态液动力Ff瞬间激增[17],后又稳定在30.6 N左右不再波动。

图5 瞬态液动力变化曲线
图6为阀芯运动速度随时间的变化规律。由图6可知,阀开启后,在Ff、Fs和Fp的共同作用下,速度呈线性增加,受Fp影响,阀芯至最大位移时,速度为0。
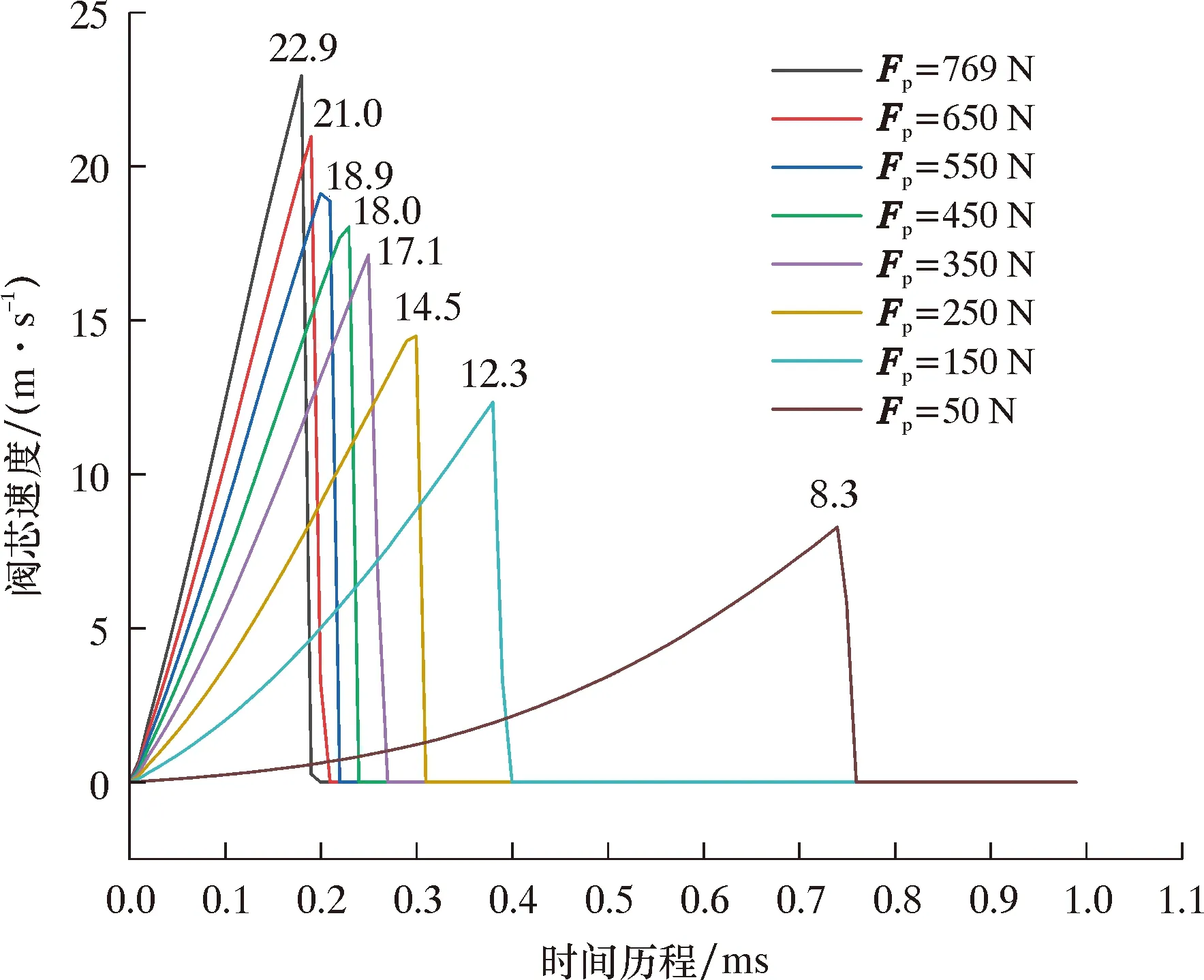
图6 阀芯速度变化曲线
图7显示了阀芯位移随时间的变化规律。由图7可知,在阀开启的瞬间,阀芯受到压差、液动力和弹簧预紧力的共同作用,随着活塞推力Fp继续推动阀芯,阀芯加速运动至位移最大值后停止运动,并在1 ms内达到了最大开度,阀芯受液压推力信号后能够迅速响应,保证了解码器的动态响应。
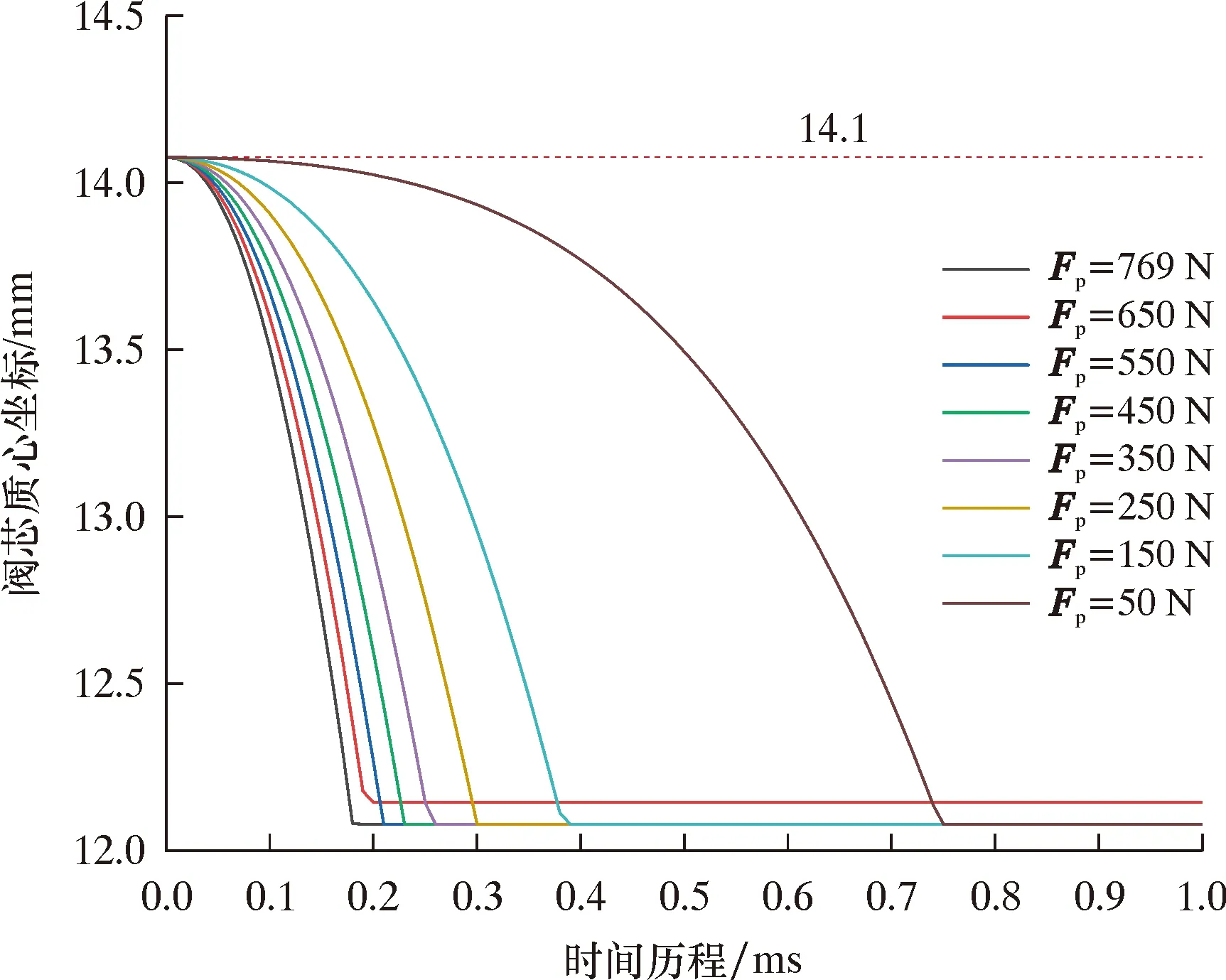
图7 阀芯位移变化曲线
3.2 压力场
图8为活塞推力作用下单向阀瞬态开启过程的部分静压云图。由图8可知,在开启初始,阀芯前后端流场压力变化显著,在开启过程中,此处阀芯承受着较大压力,阀芯顶部(球形部分)在整个过程中都承受一定的背压,故阀芯小球上半部压力较大。当阀达到最大开度后,对于阀芯周围流场,最大静压在出口区域。
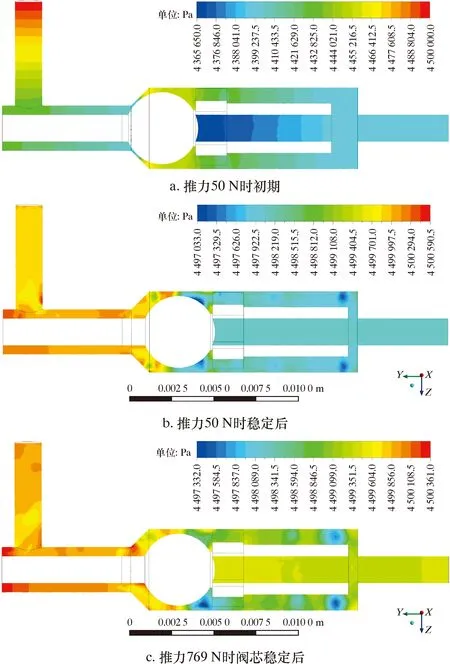
图8 活塞推力作用下单向阀瞬态开启过程的部分静压力云图
3.3 速度场
图9为瞬态开启过程中各特征时刻的速度分布云图。由图9可知:同一时刻内,阀芯顶部与阀腔喉部区域具有最高流速,而阀的顶部和底部流速相对较小;开启过程中的最大流速区域如图9a所示,此时的喉部油液最大流速高达10.4 m/s,当阀芯完全开启后,流速降低至2.7 m/s左右。

图9 瞬态开启过程中各特征时刻的速度分布云图
图10为单向阀流线及阀芯表面压力云图。由图10可知,阀芯表面受力不均,背压集中在小球顶部,在入口后方区域与阀芯底部形成涡流,阀芯上下部分环空横截面积突然改变导致流体流向改变,在此处形成了一对流向相反的涡流区,有较大能量损失。
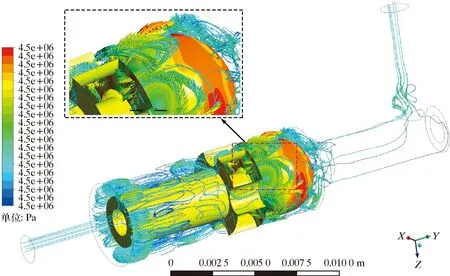
图10 阀芯压力分布和速度矢量图
4 结 论
本文基于CFD有限元软件Fluent建立了一种应用于智能完井井下解码器内部精细的微型液控单向阀三维数值模型,编译了一套新的UDF程序来控制阀芯在开启过程中的运动特性,利用动网格更新技术,实现了单向阀由关闭状态至完全开启的高速通流过程的动力学响应,取得良好的预测结果,并得到如下结论。
(1)基于Fluent 6DOF理论和新的UDF程序,提出了一种研究液控单向阀流固耦合分析的数值模型,新开发的UDF支持Fluent并行计算,大大提高了数值计算的效率。同时验证了使用微型液缸-单向阀系统作为解码器基本控制单元的可行性与可靠性。
(2)Fluent软件中的动网格技术和非稳态求解器可以很好地解决阀门开启过程中内部流道强湍流问题,可以准确地模拟出液压油在不同时刻的流动状态。
(3)使用新的研究方法将活塞动态推力Fp简化成一个大小固定的力来分析该单向阀的开启过程的动力学响应,Fp的大小直接影响阀芯能够获得的最大速度值,但对终态流场影响较小。
(4)单向阀在开启时阀的底部和顶部区域流体运动最为剧烈,阀内流体最高流速为10.4 m/s,而阀芯的运动速度达22.9 m/s,能够迅速实现动作响应,但要避免单向阀入口压力过高而出现剧烈的压力波动情况,应正确使用单向阀,以发挥其最佳性能并延长使用寿命。
