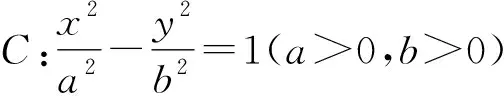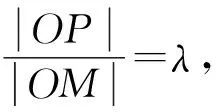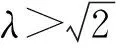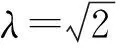2009年新课标高考理数第20题解析几何的探究

杨雪苹

(广东省广州大学附属中学南沙实验学校 511458)

圆锥曲线是高考的重要考点，在解题中涉及到函数与方程、不等式、三角和直线等内容，体现各种能力的综合要求，要求学生有较高的计算水平、较强的计算能力.求曲线轨迹方程常用方法有：直接法、定义法、代入法、参数法.求轨迹方程，一定要注意轨迹的纯粹性和完备性.要注意区别“轨迹”与“轨迹方程”是两个不同的概念.

1 试题呈现

题目(2009年新课标20)已知椭圆C的中心为直角坐标系xOy的原点，焦点在x轴上，它的一个顶点到两个焦点的距离分别是7和1.

(1)求椭圆C的方程；

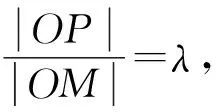
2 试题解析

2.1 题型分析

求圆锥曲线的标准方程是作为高考解答题中的第(1)问，最常见的方法是定义法与待定系数法.本题中第(1)问考查待定系数法求圆锥曲线的标准方程.

离心率是高考对圆锥曲线考查的重点，涉及a,b,c三者之间关系.本题的第(2)小题是考查圆锥曲线垂直相关点的轨迹问题，是比值为离心率e时的一般化变式：

2.2 解法探究

由椭圆定义知：到两个焦点的距离分别是7和1的顶点一定是长轴两端点中一个.

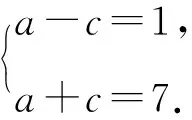
解得a=4,c=3.

所以b2=a2-c2=16-9=7.

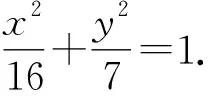
(2)设M(x,y)，其中x∈[-4,4].

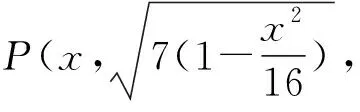
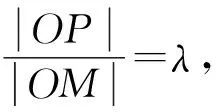
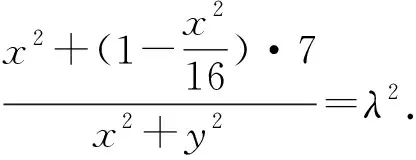
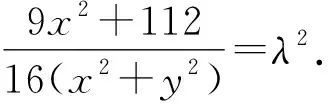
整理,得(16λ2-9)x2+16λ2y2=112，其中x∈[-4,4].

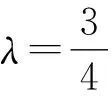
化简,得9y2=112.

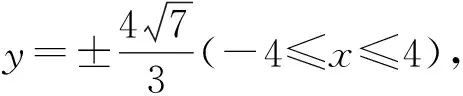
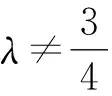
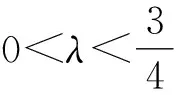
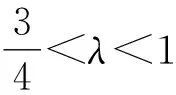
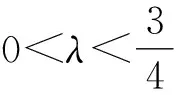
小结本题第 (1)小题主要考查椭圆的基本性质；在第(2)小题中， 点M的轨迹方程通过直接将相关点的坐标代入等量关系，考查形如(λ-a)x2+bλy2=c(其中a,b,c为定值)的动点的轨迹，渗透着分类讨论思想.若把载体变为双曲线，问题该如何解答呢？

3 试题变式

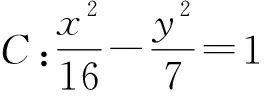
解析设M(x,y)，其中x≥4或x≤-4.

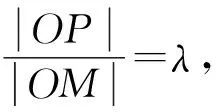
由于点P在双曲线上，可得

即(23-16λ2)x2-16λ2y2=112，其中x≥4或x≤-4.

因为(23-16λ2)x2=16λ2y2+112>0,

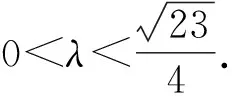
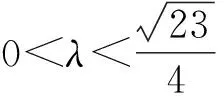
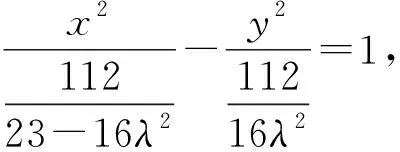
即23-16λ2≥7，即0<λ≤1时，

点M的轨迹为中心在原点、实轴在x轴上的双曲线满足x≥4或x≤-4的部分；

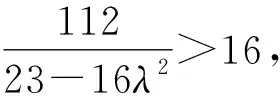
4 结论的一般化及推广

4.1 结论的一般化

当0<λ

当λ=e时，点M的轨迹是两条平行于x轴的线段；

当e<λ<1时，点M的轨迹为中心在原点、长轴在x轴上的椭圆满足-a≤x≤a的部分；

当λ≥1时，点M的轨迹为中心在原点、长轴在x轴上的椭圆.

4.2 结论的推广

当0<λ≤1时，点M的轨迹是中心在原点、实轴在x轴上的双曲线满足x≥a或x≤-a的部分；

当1<λ

当λ≥e时，点M的轨迹不存在.