椭圆切线方程的推导及其简单运用

武增明

(云南省玉溪第一中学 653100)

证法1 (判别式法)[4]当过椭圆上一点P(x0，y0)的切线的斜率存在时，设切线方程为y=kx+m，将其代入椭圆方程b2x2+a2y2=a2b2，化简并整理得(a2k2+b2)x2+2a2kmx+a2m2-a2b2=0.

因为直线与椭圆相切，

所以Δ=(2a2km)2-4(a2k2+b2)(a2m2-a2b2) =0，

化简得a2k2-m2+b2=0.

当过椭圆上一点P(x0，y0)的切线的斜率不存在时，切线方程为x=±a，满足上式.

证法2 (判别式法)[3]当过椭圆上一点P(x0，y0)的切线的斜率存在时，设切线方程为y-y0=k(x-x0)，即y=kx-kx0+y0.

将其代入椭圆方程b2x2+a2y2=a2b2，

化简并整理得(a2k2+b2)x2+2a2k(y0-kx0)x+a2(y0-kx0)2-a2b2=0.

因为直线与椭圆相切，所以有

Δ=4a4k2(y0-kx0)2-4a2(a2k2+b2)[(y0-kx0)2-b2]=0.

从而可解得

故切线方程为

进一步化为

所以b2x0x+a2y0y=a2b2.

当过椭圆上一点P(x0，y0)的切线的斜率不存在时，切线方程为x=±a，满足上式.

所以在点P(x0，y0)处的切线的斜率为

以下同证法2.

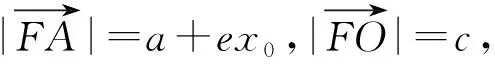
在研究此题的解答时，发现此题可以引申、推广得到如下圆锥曲线的两个美好性质.

证明略，留给感兴趣的读者朋友证明.

(1)已知直线l的斜率为k，用a，b，k表示点P的坐标；

(2)若过原点O的直线l1与l垂直.证明：点P到直线l1的距离的最大值为a-b.

解析(1)设P(x0，y0)，

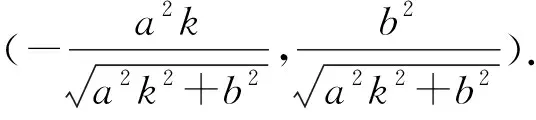
(2)依题意得直线l1的方程为a2y0x-b2x0y=0.故P(x0，y0)到直线l1的距离为

所以由柯西不等式得

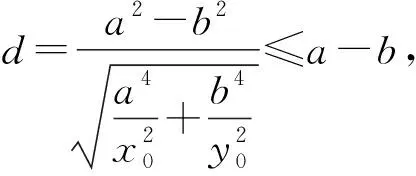
所以点P到直线l1的距离的最大值为a-b.

过双曲线和抛物线上一点P(x0，y0)的切线方程的推导方法可类比于过椭圆上一点P(x0，y0)的切线方程的推导方法，在这里限于篇幅，推导从略，读者朋友不妨试一试.