三道2021年高考数学试题的答案解析

胥植麟

(云南省昆明市云南师范大学 650500)

题1 (2021年高考数学乙卷20)设函数f(x)=ln(a-x).已知x=0是函数y=xf(x)的极值点.

(1)求a；

解析(1)因为y=xf(x)=xln(a-x)，

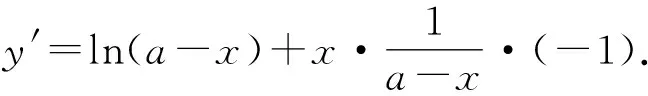
因为函数y=xln(a-x)在x=0处可导，且在x=0处取得极值，

所以根据费马引理，得

f′(0)=0.

即lna=0，解得a=1.

(2)根据第(1)问,得

f(x)=ln(1-x).

题目要证明g(x)<1，

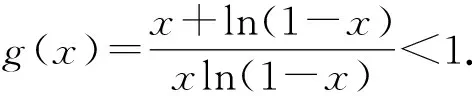
拆成两项,得

就是要证明

就是要证明

(Ⅰ)

由g(x)的函数关系式，得

g(x)的定义域为x<1且x≠0.

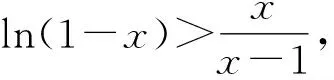
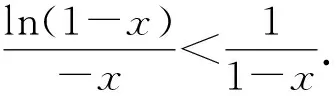
(Ⅱ)

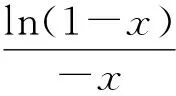
令φ(t)=lnt,则函数在[1-x,1]内连续，(1-x,1)内可导，根据拉格朗日中值定理，

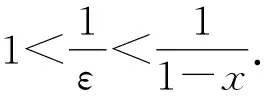
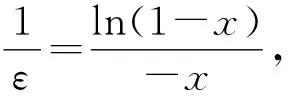
所以(Ⅱ)式成立.

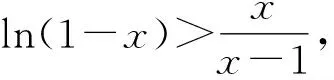
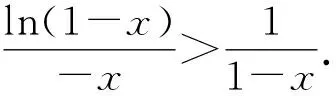
(Ⅲ)

同样根据拉格朗日中值定理，令φ(t)=lnt,

则函数在[1,1-x]内连续，(1,1-x)内可导，

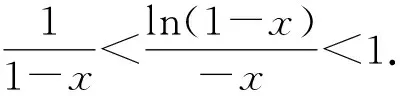
所以(Ⅲ)式成立.

综上所述,当x<1时,g(x)<1成立.

题2(2021年高考数学乙卷21)已知抛物线C：x2=2py(p>0)的焦点为F，且F与圆M：x2+(y+4)2=1上的点的距离最小值为4.

(1)求P；

(2)若点P在M上，PA，PB是C的两条切线，A，B是切点，求△PAB面积的最大值.

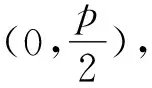
所以抛物线C的方程为x2=4y.

(2)连接AB，由于AB是抛物线C的弦，而PA,PB又是抛物线C的切线，则△PAB为阿基米德三角形.

由于PA,PB的交点P在圆M上，而圆M上的任意一点都不在抛物线C的准线上，故弦AB一定不过焦点(0，1).

设点A坐标为(x1,y1)，点B坐标为(x2,y2),

则PM为△PAB的中线.

根据阿基米德三角形的性质，PM∥y轴.

设弦AB所在的直线方程为y=kx+b，

代入抛物线C的方程，得

x2-4kx-4b=0.

根据韦达定理，得

x1+x2=4k,x1x2=-4b.

所以点M坐标为(2k,2k2+b)，

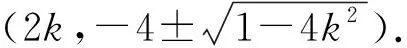
因为PA，PB是抛物线的切线，

所以可以得到两条切线方程，分别是

yPA：xx1=2(y+y1)，

yPB：xx2=2(y+y2).

两式相加,得

x(x1+x2)=2(2y+y1+y2).

又x1+x2=4k,y1+y2=k(x1+x2)+2b，

点p的横坐标为2k，

联立得点p的纵坐标为-b.

所以点p为(2k，-b)，

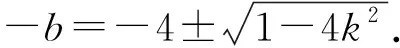
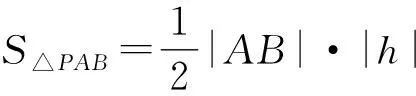
化简，得

因为面积要最大值,所以负号的情况省略，即

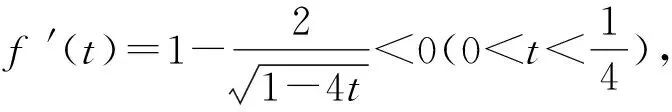
所以f(t)max=f(0).

所以△PAB面积的最大值在k2=0时取到.

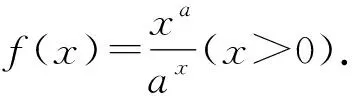
(1)当a=2时，求f(x)的单调区间；

(2)若曲线y=f(x)与直线y=1有且仅有两个交点，求a的取值范围.

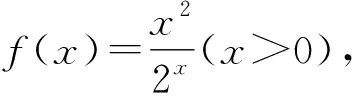
令f′(x)=0,因为x>0，2x>0，

所以2-xln2=0.

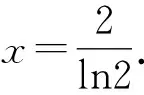
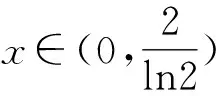
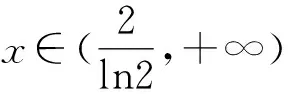
因为x>0，所以两边取对数，得lnxa=lnax.

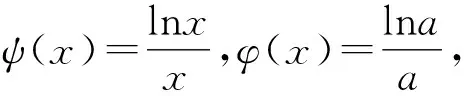
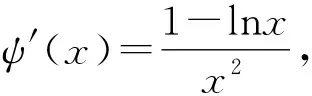
由1-lnx=0，解得x=e.

当00，则ψ(x)单调递增；

当x>e时，ψ′(x)<0，则ψ(x)单调递减.

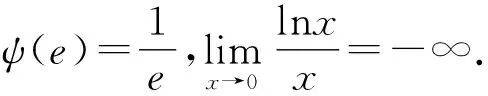
当x趋近于无穷时，

由于有不等式

lnax1,β>0)，

如图1，ψ(x)与φ(x)在x>0时有两个交点.

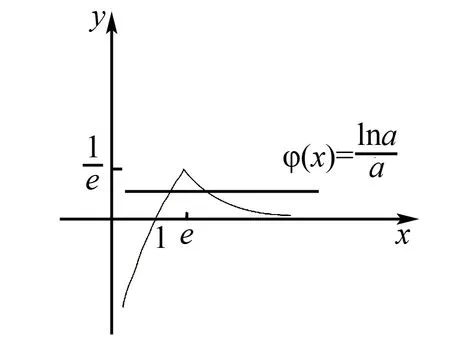
图1

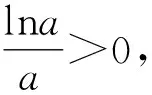
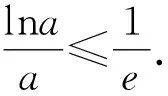
所以只要令a≠e即可满足条件.

综上所述，a>1且a≠e.