利用导数突破高考圆锥曲线压轴题
2022-02-25贺凤梅
贺凤梅
(新疆伊犁巩留县高级中学 835400)
1 题目呈现
题目(2021年普通高等学校招生全国统一考试全国乙卷理科 第21题) 已知抛物线C:x2=2py(p>0)的焦点为F,且F与圆M:x2+(y+4)2=1上点的距离的最小值为4.
(1)求p的值;
(2)若点P在M上,PA,PB是C的两条切线,A,B是切点,求ΔPAB面积的最大值.
2 总体分析
本题是全国乙卷理科解答题的第21题,属于压轴题,以面积最值为命题点,综合考查圆锥曲线和导数.圆锥曲线中的最值问题解决方法一般分两种:第一种是几何法,特别是利用圆锥曲线的定义和平面解析几何的有关结论来求最值;第二种是代数法,常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题,然后利用基本不等式、函数的单调性或三角函数的有界性等来求解最值.另外,导数的几何意义的引入也大大丰富了高中数学的知识体系,给我们用常规方法无法解决的问题提供了新的视角,同时也拓宽了解决圆锥曲线问题的思路.下面从不同的视角来探讨这个高考压轴题,并进行追根溯源,深刻理解此问题的本质,期望弄通悟透.
3 试题解答

以下重点探讨第(2)问.
视角1借助导数的几何意义,同一法求直线方程,进而求面积的最值
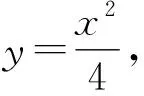
①
②
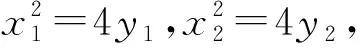


化简整理,得x2-2x0x+4y0=0,
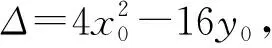
由韦达定理有x1+x2=2x0,x1x2=4y0,



由条件易知y0∈[-5,-3].

视角2借助导数的几何意义,斜截式求直线方程,进而求面积的最值.


③


在进行道床建设时,要保证材料符合相关的标准要求,加强道床施工的质量控制,保证其具有较高标准的承载力,可以在较长时间承载地铁的运行,有以下技术要点:①在道床施工中,要将预留缝隙与隧道结构缝控制在统一平面上;②在搭设与拆除脚手架时要与钢轨置离;③进行混凝土浇筑时要适当的分层,采用特殊的方法分台阶浇筑,保证其具有充足的承载力。
评注此解法同解法1,先得出切线PA,PB的方程,联立两直线方程得出交点P的坐标(用点A,B的横坐标表示);再设直线AB的斜截式方程,与抛物线方程联立,借助韦达定理得出两根之和与两根之积.接下来进行对照,将点P的坐标用直线AB方程斜截式中的k和b来表示,最后利用面积公式并结合解法1可得解.
视角3借助导数的几何意义及数形结合思想,求出面积表达式,进而求面积的最值.
解法3 设A(x1,y1),B(x2,y2),P(x0,y0),由解法2可得

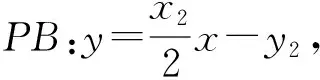

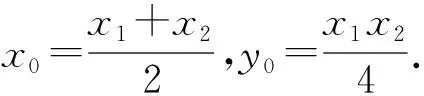
设AB中点为Q,则由中点坐标公式可得点
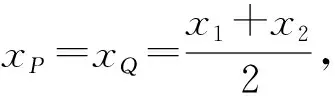
所以|PQ|=|yQ-yP|.



评注此解法关注到点P的横坐标与弦AB中点Q的横坐标相同,因此PQ⊥x轴,从而简化了面积的转化与求解,这也体现了数形结合思想的重要性.由此解法我们得到的启示是:在做直线与圆锥曲线的综合题时,先做草图,数形结合,也许可以找到解题的突破口.
4 追根溯源

(1)求p的值;
(2)当M在C2上运动时,求线段AB的中点N的轨迹方程.
评注此题也有多种解法,可以直接设切点的坐标,利用导数的几何意义得出切线方程,再利用求轨迹的方法求解.此法的关键点是设而不求,思路直接,难点是参数多,需要注意消参的技巧;也可以借助抛物线的参数式,利用导数求出切线的方程,进而求出两切线的方程,转化为以t1,t2为两根的方程,最后利用韦达定理求解,关键点是方程的转化和消元的技巧.此题解法从略,有兴趣的读者可以自己尝试.
从近几年全国各地的高考圆锥曲线的压轴题来看,圆锥曲线的定义、几何性质及直线与圆锥位置关系仍是高考的热点和难点.文中两题以圆锥曲线中的抛物线为背景,过曲线外一点引曲线两条切线问题为载体展开.一道题是利用导数求切线斜率,并求所得到的三角形面积的最大值;另一道是利用导数求切线斜率,寻求动点轨迹方程.两题均考查了圆锥曲线的一些基本知识及消参等基本运算;从思想方法上来看,考查了数形结合思想、函数与方程思想等.
要学好高中数学,就应该对所学知识有整体的认识和把握,即理解这些知识在解决数学问题乃至实际问题中所起的作用.我们也要明确,数学是思维的科学,逻辑思维、数形结合、概括与综合等都是数学的重要思想方法.