横隔板间距对钢箱梁扭转畸变的影响分析

张辉军

（中建三局工程设计有限公司，湖北 武汉 430074）

1 工程概况

湖北鄂东长江公路大桥（以下简称“鄂东大桥”）位于长江中游黄石市与鄂州市交界区域，是沪蓉高速公路湖北省东段（武黄高速公路和黄黄高速公路）和国家高速公路网大庆至广州高速公路湖北段的共用过江通道。大桥全长6203.0m，主桥为双塔双索面混合梁斜拉桥，跨径布置为3×67.5m+72.5m+926.0m+72.5m+3×67.5m。主跨为926m，仅次于香港昂船洲大桥，居世界同类型桥梁第二。

鄂东大桥主跨钢箱梁采用低合金高强度结构钢Q345q-D，为分离式双箱断面（见图1），梁中心线处内轮廓高3.8m，全宽为38m（含布索区和风嘴），桥面设置2%双向横坡。桥面顶板、底板、下斜底板及中纵腹板纵向主体均采用U形加劲，边纵腹板及顶板、下斜底板的边角部分采用板式加劲；边纵腹板设置三道板式加劲，两道通长，一道位于斜拉索锚固区范围。钢箱梁横隔板间距3m，分为B1、B2、B3三种。B1类用于斜拉索处，B2类为普通横隔板，B3类用于钢箱梁过渡段，厚度分别为14mm、12mm、16mm。

图1 鄂东大桥钢箱梁标准断面图

2 正交异性板钢箱梁的受力特点

薄壁箱形梁具有薄壁杆件的特性，应力、变形情况比较复杂。作用于箱形梁的外力可综合表述为偏心荷载下的结构分析,其变形和位移可分解为纵向弯曲、横向弯曲、扭转及畸变4种基本状态[1]，如图2所示。箱梁在偏心荷载作用下，因弯矩作用在横截面上，将产生纵向弯曲正应力σM和剪应力τM。对于宽高比较大的正交异性板钢箱梁，还需要考虑剪力滞效应的影响。因扭转变形将在箱梁各板中产生横向弯曲应力和剪应力。其中，箱梁扭转包括自由扭转和约束扭转。自由扭转为假定无纵向约束的刚性转动，截面纤维纵向变形自由，但保持截面周边投影不变形，此时仅产生自由扭转剪应力τK。约束扭转时，截面纵向纤维变形受到强大横隔板等的约束，截面沿桥纵向自由变形受到约束而不能自由翘曲，产生翘曲正应力σW和约束扭转剪应力τW。畸变是由于钢箱梁各板件的宽厚比较大，箱形截面受扭后无法保持截面投影仍为矩形，截面周边发生了变形，产生畸变正应力σdW和畸变剪应力τdW。同时，由于畸变箱形截面板件发生横向弯曲，在板内产生横向弯曲应力σdt。在集中荷载作用下的箱梁板件，除了直接受力部分产生横向弯曲外，由于截面的框架效应，引起其他板件也产生横向弯曲，在纵截面产生弯曲正应力σc。

图2 箱形梁偏心荷载下的受力分解图示

因此，箱形梁纵、横截面上的应力可以表示如下：

横截面正应力：σZ=σM+σW+σdW

横截面剪应力：τ=τM+τK+τW+τdW

纵截面弯曲正应力：σS=σdt+σc

3 有限元模型的建立

扭转、畸变及横向弯曲效应引起的正应力，在通常的解析方法中是将它们分开考虑。而事实上，扭转与畸变是相互耦合在一起的。本文采用ANSYS分析时，将扭转畸变正应力作为一项指标进行处理，即同一荷载在偏心作用和中心作用下产生的纵向应力之差。这样计算结果更加接近实际情况。

截取5段标准钢箱梁建立有限元模型，其力、位移边界条件均与杆系模型下的计算结果保持一致，斜拉索以同刚度的弹簧单位等效。横隔板的间距采用6种方式布置（见表1）。在横隔板间距变换过程中，保持拉索处B1横隔板位置不变，分别建立模型，见图3。

表1 横隔板布置情况

图3 五跨钢箱梁有限元模型

由于不关心车辆荷载作用位置的局部应力情况，将三辆550kN车辆荷载简化为1.2m×0.2m面荷载按中心加载和偏心加载两种情况施加。中心荷载施加在第二跨梁末端桥中心处，偏载施加在第二跨梁末端左幅边纵腹板顶板上。选取左右中纵腹板上下四个角点第三跨沿轴向作为应力提取路径，计算分析各种横隔板间距下截面的扭转畸变正应力，得出其扭转畸变正应力分布图（见图4），图中横坐标起点为第三段钢箱梁的起点[2]。

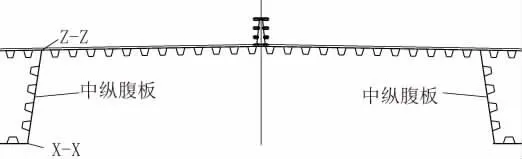
图4 应力选取路径示意图

4 扭转畸变正应力分析

由图5可知，当没有设置横隔板时，Z-Z路径的扭转畸变正应力较大，在第三段梁内基本为压应力。最大压应力为78.1MPa，出现在梁端起点处。设置1道横隔板后，Z-Z路径起点处扭转畸变应力仍为最大压应力，但是已经降为55.685MPa，相对于无横隔板时下降了22.415MPa，降幅28.7%。当设置3道横隔板时，扭转畸变应力大幅减小，最大扭转畸变拉应力为2.42MPa，最大扭转畸变压应力为2.81MPa，相对于1道横隔板时减小52.875MPa，减幅为94.95%。

图5 Z-Z路径扭转畸变正应力

由图6可知，X-X路径上无横隔板时，扭转畸变正应力均为拉应力，最大值也出现在梁端，大小为37.86MPa。增设1横隔板后，最大扭转畸变拉应力减小为11.513MPa，相对于无横隔板时减小了69.59%。此时在横隔板处扭转畸变应力产生一处2.637MPa的应力变化，最小拉应力0.46MPa，之后开始出现压应力。这是由于横隔板在其平面内具有很大的刚度，能较好地约束箱梁腹板和顶底板的变形，使横隔板、顶底板、腹板组成的闭合箱梁的抗扭刚度得到了很大的提高。

图6 X-X路径扭转畸变正应力

对比上面的分析，这种由于横隔板对畸变的限制形成的扭转畸变应力变化在Z-Z路径上并不明显，这说明横隔板的作用在底板更加显著。因此，当钢箱梁增设1道横隔板后，不论是对弯曲应力还是扭转畸变应力，均有明显改善。设置3道横隔板时，扭转畸变应力均为压应力，大小基本在2MPa以内，最大压应力为2.76MPa，相对于只有1道横隔板时减小了123.94%。可以明显看到，此时钢箱梁顶、底板的扭转畸变应力都得到了很好的控制，可以认为钢箱梁在整个梁段内均不产生畸变。

由图7可知，当横隔板数目增加到4道、5道、6道时，与设3道横隔板时相比，扭转畸变应力的大小没有随着横隔板的增加有明显改善，且不是严格按照横隔板数目的增加而减小。在梁端4m外，即经过2道横隔板后，扭转畸变应力基本已在0.5MPa以内，可以认为钢箱梁不再发生扭转畸变[2]。

图7 Z-Z路径扭转畸变正应力

由图8可知，在X-X路径上，当横隔板数目增加到4道、5道、6道时，扭转畸变应力变化已不明显。各路径在不同横隔板布置下的最大扭转畸变正应力汇总见表2。

表2 各路径在不同横隔板布置下的最大扭转畸变正应力（单位：MPa）

图8 X-X路径扭转畸变正应力

5 结 语

结合鄂东大桥实例，采用ANSYS建立实体模型，计算分析了6种不同横隔板间距对钢箱梁在偏心荷载作用下的扭转畸变正应力的影响情况。当不设置横隔板时，由于偏心活载带来的扭转畸变应力值达到了78.1MPa，轴向压应力达到286.35MPa，已远超过Q345的设计容许应力。当设置3道横隔板时，可以将扭转畸变应力控制在5.36MPa以内，已经能够适用于实际工程。再增加横隔板数量时，扭转畸变应力并没有实际的改善。