中国粮食总产量影响因素分析

□文/史春红

（首都经济贸易大学 北京）

［提要］通过多元线性回归方法，从土地因素、自然因素、科技因素以及劳动力因素等四个方面分析中国粮食总产量的影响因素，发现粮食播种面积、农用化肥施用量和受灾面积是影响粮食生产的三大因素，并从多个方面提出增加中国粮食产量的建议。

我国是粮食生产与消费大国，政府一直十分重视粮食问题。中国的粮食状况如何、中国的粮食生产潜力有多大、中国人民能不能养活自己、中国将如何发展粮食生产，都是人们普遍关心的问题。

一、中国粮食生产发展阶段划分

我国粮食生产的发展，大致分为三个阶段：

第一阶段为1950～1978年。新中国刚刚成立，这个时期我国一方面改革了土地所有制关系，引导帮助农民走上了互助合作的道路，解放了生产力；另一方面改善了农业基础设施，提高了农业物质装备水平，加快了农业科技进步，为粮食生产的持续发展奠定了基础。

第二阶段为1979～1984年。这个时期是新中国建立以来粮食增长最快的时期，主要是因为我国政府在农村实施的诸多措施。我国进行农村改革，实行家庭联产承包责任制，改革农产品购销制度，允许自由买卖，极大地提高了农民的生产积极性；再加上杂交水稻的推广，从而成为新中国建立以来粮食数量增长最快的时期。

第三阶段为1985年至今。这一时期，我国政府在一方面继续发展粮食生产；另一方面进行了农业生产结构调整，发展了多种经营，食物多样化发展较快，提高了人民的生活质量。

目前，我国已经基本解决了城乡居民的温饱问题，政府今后的任务是一方面进一步增加粮食总量；另一方面努力发展食物多样化的生产，调整食物的结构，进一步提高人民的生活质量。而且，我国政府也清醒地看到，我国粮食供需平衡的水平还需要进一步提高，供需偏紧的状况还将长期存在。

粮食是人类生命得以延续的最基础的物质条件。随着技术水平的提高、社会的发展，从整体来讲我国粮食产量呈上升趋势。在改革开放（1978年）之前，我国粮食产量增长非常缓慢，一直都在30，000万吨以下。改革开放后，粮食产量从30，000万吨一路疯狂走高，粮食生产飞速发展，但产量波动也更频繁。从2000年开始出现几年连续减产的现象，产量曾一度降到43，070万吨，一下子退回到十几年前的水平。从2007年以来，我国粮食连续增产，在2018年粮食总产量达到65，789万吨。

我国的人口数量每年都在增加，耕地面积却不断减少。但是，耕地面积减少，粮食总产量却没有降低，这可能是其他影响因素带来的。如果粮食总产量降低，我国就会到国际市场去购买粮食，从而导致粮食价格大幅度上涨，最坏的可能是引起世界性饥荒。也就是说，中国粮食总产量影响中国的粮食价格甚至是全球的粮食价格。所以，粮食对国家的影响是非常重大的，分析影响粮食总产量的因素是非常有必要的。

二、数据介绍

样本时间资料选自《中国统计年鉴》，本文使用了1978～2018年中国粮食产量和粮食作物播种面积、受灾灾面积、耕地灌溉面积、农业化肥施用量、农用机械总动力、农村用电量以及第一产业就业人员数等数据，并对影响粮食产量的因素进行了实证分析。

我们把X1（粮食作物播种面积）看作土地因素方面的影响变量，X2（受灾面积）看作自然因素方面的影响变量，X3（耕地灌溉面积）、X4（农用化肥施用量）、X5（农业机械总动力）、X6（农村用电量）看作科技因素方面的影响变量，X7（第一产业就业人员数）看作劳动力方面的影响变量。

三、描述性分析

（一）因变量分布。图1为因变量折线图，从中可以看出，总体来讲，粮食产量是呈现上升趋势的；图2为因变量柱状图，从中可以看出，因变量近似正态分布，满足线性回归假设。（图1、图2）

图1 因变量折线图

图2 因变量柱状图

（二）变量之间的相关性分析。表1显示了所有变量之间的相关性，从表中可以看出，各个自变量与因变量之间的相关系数较大，说明存在显著的线性关系。自变量之间的相关系数较大，说明这些自变量之间存在较强的相关性，在后续建模中需要注意避免多重共线性。（表1）

表1 变量之间的pearson相关性一览表

四、基本假设的检验

将全部自变量选入，进行多重共线性检验和残差的正态性检验、异方差性检验以及自相关性检验。

（一）正态检验。图3为标准化残差图，图4为正态P-P图，都是用来正态性检验的。从图3中可以看出，残差大致服从正态分布；从图4中可以看出，各点落在对角线附近，说明残差大致服从正态分布。总之，残差满足正态性的假设条件。（图3、图4）

图3 标准化残差图

图4 正态P-P图

（二）异方差性检验。图5为残差与预测值的散点图，表2为残差与自变量之间的Spearman等级相关系数，都是用来异方差性检验的。从图5中可以看出，这些点大致均匀地分布在零值上下，说明残差基本不存在异方差性。从表2中可以看出，标准化残差与各个自变量的Spearman等级相关系数都比较小，并且P值都大于0.05，说明标准化残差与各个自变量没有显著相关性，不存在异方差。（图5、表2）

表2 残差与自变量之间的Spearman等级相关系数检验一览表

图5 残差与预测值的散点图

（三）自相关性检验。表3为DW检验，图6为et和et-1残差图，都是用来自相关性检验的。从表3中可以看出，DW值为0.543，说明残差存在一阶正自相关。从图6中也可以看出，et和et-1存在正自相关关系。（表3、图6）

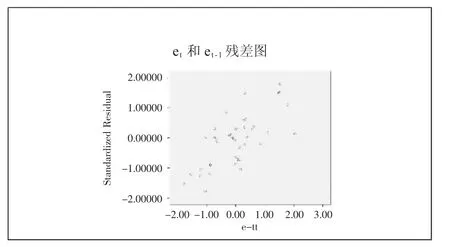
图6 et和et-1残差图

表3 DW检验一览表

（四）多重共线性检验。利用SPSS软件做多重共线性诊断，输出结果如表4所示。从中可以看出，多个自变量的VIF值远远超过10，说明这个回归方程存在严重的多重共线性。（表4）

表4 多重共线性检验一览表

五、建立多元线性回归模型

在前面的基本假设的检验中，我们知道残差满足正态性和方差齐性，但是方程不满足多重共线性。下面我们消除多重共线性并建立模型。

（一）模型建立。利用逐步回归法消除多重共线性，输出结果如表5所示。从中可以看出，最终留下了X1（播种面积）、X2（受灾面积）、X4（农用化肥施用量）这三个变量，且这三个变量的VIF值已小于10，说明消除了多重共线性。（表5）

表5 逐步回归法系数输出一览表

得到的多元线性回归模型为：

（二）模型检验。从表6中可以看出，通过逐步回归消除多重共线性后，R2=0.955，说明拟合效果较好；从表7中可以看出，F值为263.226，P值=0.00，说明模型显著。（表6、表7）

表6 模型拟合一览表

表7 方差分析一览表

六、结论及建议

（一）结论。多元线性回归模型为：

粮食产量=-21483.016+0.470×粮食作物播种面积+（-0.097）×受灾面积+5.556×农用化肥施用量

从土地因素来看，粮食作物播种面积与粮食产量呈正相关，在一定条件下，增加粮食作物播种面积能够增加粮食产量；从自然因素来看，受灾面积与粮食产量呈负相关，在一定条件下，减少受灾面积能够增加粮食产量；从科技因素来看，农用化肥施用量与粮食产量呈正相关，在一定条件下，增加农用化肥施用量能够增加粮食产量。本文通过计量经济分析方法，对影响程度有了更加精确的评估，事实上影响粮食生产的因素不仅多而且复杂，我们不可能逐个引入模型，只能根据因素自身重要程度、数据取得难易程度、模型的数学条件等进行适当取舍，因此很可能存在一定误差。

（二）建议。从以上研究分析来看，受灾的面积与粮食产量成负相关，也就是说受灾的面积越大，粮食产量越低。所以，想要提高我国粮食的生产量，就要尽量降低自然灾害。要加强气象预报功能和农田水利基本设施建设；向农业推广抗灾减灾技术，加快基础设施建设，加强减灾体系建设等，从而把自然灾害的影响降到最低。

从上述粮食产量的多元线性模型来看，播种面积也是一个重要的因素。现在我国的退耕还林力度加大，使得粮食播种面积大幅度减少。近期还出现严重的违规占地现象，这都影响粮食产量。因此，要落实耕地保护政策，稳定粮食播种面积，执行基本农田保护制度，不断提高粮食生产能力。

我国农业机械普遍使用，促进了粮食生产，从相关系数来看，农机也是相关影响因素之一。我国农业劳动生产率的提高很大程度上取决于农机使用率，应调整农业的产业结构，在适宜的地区发展农业机械化，转变农业增长方式，提高粮食产量。

从国家层面来看，我国应该努力改善生产条件，千方百计提高粮食综合生产能力。为了实现粮食增产的目标，我国政府采取了一系列措施。比如，保护耕地资源，制定和完善了《农业法》《土地管理法》以及《水土保持法》等一系列法律法规，抑制了耕地面积锐减势头；增加农业投入；加强水利建设，政府领导人民治理江河、拦洪蓄水、改善生产条件，修建水库、改造易涝地等，有效地提高了农业抗灾能力；提高农业的物质装备水平，一方面大力发展了国内化肥生产，提高化肥的自给率，另一方面积极推进农药、农膜、农机、农电、柴油等农用工业的发展，只为全面提高粮食综合生产能力。

我国应该综合开发利用山地、水面、草原等国土资源，增加各类食品产量，更多地增加肉类、禽蛋、奶类、水产品、蔬菜、水果等食品的供给。同时，注意保护农业资源，改善生态环境，实现农业可持续发展。措施如下：逐步建立符合我国资源特点的畜牧业生产结构；继续坚持“以养殖为主，养殖、捕捞、加工并举”的方针，积极扩大内陆淡水养殖面积，进一步开发利用浅海滩涂，发展远洋捕捞；巩固完善大中城市蔬菜生产基地，鼓励农区通过间作套种等多熟制栽培措施，发展蔬菜生产，稳定提高蔬菜均衡供给水平和有效供给能力；实现粮食生产的持续稳定增长，发展食物多样化生产，还需处理好人口、资源、环境的关系，加强农业资源管理，保护生态环境。

总之，粮食生产问题是一个复杂的问题，经过分析，粮食产量主要受到化肥施用量、播种面积和受灾面积等因素影响。面对这些因素，要着手于解决方案，逐个研究和分析，从而达到增加和稳定粮食产量的目的。■