在实验室中模拟引力透镜效应以及系外行星的搜寻

苏 俊 谢基伟 潘苏东 王思慧 翁雨燕

（1.华东师范大学教师教育学院，上海 200062；2.江苏省海安高级中学，江苏 海安 226600；3.南京大学天文与空间科学学院，江苏 南京 210023；4.南京大学物理学院，江苏 南京 210023；5.苏州大学物理科学与技术学院，江苏 苏州 215006）

1 引言

我们经常看到哈勃望远镜拍摄的引力透镜照片，什么是引力透镜，它是怎样形成的？这是很多中学师生非常感兴趣的问题.根据爱因斯坦的广义相对论，当光线经过大质量天体附近时会发生偏转，形成引力透镜效应，类似于一个光学透镜对光线的折射.在美国高中物理教材《科学发现者：物理原理与问题》中有不少物理前沿知识的介绍，其中在光学基础部分介绍了引力透镜效应.［1］另外，引力透镜效应在亚洲物理奥林匹克竞赛和泛珠三角物理邀请赛等中学生物理竞赛中也作为试题出现过.［2］图1（a）为引力透镜示意图，背景光源发出的光经过前方天体发生偏转，形成扭曲的像；图1（b）为哈勃望远镜拍摄的爱因斯坦圆环，背景天体的光线被前景天体扭曲，呈现环状的像.

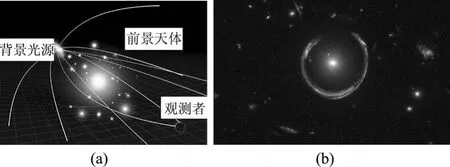
图1 引力透镜效应

2019年诺贝尔物理奖颁发给了两个领域，表彰詹姆斯·皮布尔斯教授对物理宇宙学的理论贡献；同时授予米歇尔·梅耶教授和迪迪埃·奎洛兹教授，他们利用径向速度法第一次发现了一颗围绕类太阳恒星运行的系外行星飞马座51b，［3］开启了人类对太阳系外行星与生命的探索.根据exoplanet.eu官网统计，至今人类已经发现4000多颗系外行星.系外行星的主要搜寻方法有径向速度法、凌星法、微引力透镜法.径向速度法和凌星法是目前系外行星的主要搜寻方法，笔者在之前的工作中介绍了这两种方法.［4］当一个系外行星经过背景光源与观测者之间，行星的引力也会使得光线发生微弱的偏转，使得背景光源的亮度出现涨落，这种现象称为“微引力透镜效应”（为简化问题，接下来我们统称引力透镜效应），利用这种引力透镜效应也可以进行系外行星的搜寻.

在物理教育教学过程中，适当给中学生拓展科学前沿知识是值得尝试的，有利于培养中学生的科学素养，拓宽学科视野.引力透镜效应是我们在天文照片上看到的现象，我们能否在实验室中真实模拟出引力透镜效应？

1969年SidneyLiebes等人构建了一个与引力透镜等效的物理模型，为在实验室中模拟引力透镜效应提供了可能.［5］但是，在当时要制作出满足特定函数曲面的透镜在技术比较繁琐.3D打印技术在近些年得到了快速发展，打印精度和速度不断提高，同时打印成本也在不断降低，在很多中学的实验室也会配备3D打印机.光敏树脂3D打印机的出现使得打印透镜成为现实.这里，我们利用了3D打印技术来制作满足特定函数曲面的透镜.

本文将首先介绍引力透镜效应的基本原理，然后描述利用3D打印技术制作引力透镜的方法，再从实验上模拟引力透镜效应的主要特征以及系外行星的搜寻.

2 引力透镜的原理

根据爱因斯坦广义相对论，由于引力场的作用，当光线经过质量为M的天体附近时，光线会发生偏转，当偏转角α很小时，α近似表示成［6］

其中G为万有引力常数，r为碰撞参数，c为真空中的光速.

光线在引力场中的偏转会产生引力透镜效应，下面我们来分析最简单的情形，如图2，点质量天体M充当一个“透镜”，记作L，点光源S发出的光经过点质量天体M附近发生偏转，观测者从O点观测光源S的像.其中DL为L与O的距离，DLS为L与S的距离，DS为O与S的距离，θS为S相对于L、O连线的张角，θI为S的像I相对于L、O连线的张角.由于天体间的距离比较远，以下计算均认为这些角度很小.

图2 引力透镜效应

由图2可知θIDS=θSDS+αDLS，其中r≈θIDL，利用（1）式可得

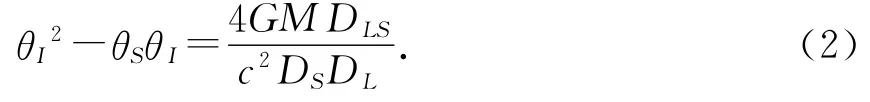
当三者共线时，θS=0，可得像的张角为，S的像是一个对称的环，称为爱因斯坦圆环，张角θI记作θE，即

若S与L、O的连线不共线，（2）式有两解

光源S有两个像，张角分别为θ1与θ2，其中张角为θ1的像位于爱因斯坦圆环外侧，张角为θ2的像位于爱因斯坦圆环内侧.可以证明，两个像总的光强Itot会大于光源S原有的光强IS，且Itot表示为［7］

当点质量天体M以一定速度v垂直视线方向经过恒星S与观测者O之间时，根据（5）式，微弱的引力透镜效应会使得恒星S亮度出现涨落，光变曲线如图3.当一个恒星 -行星系统经过恒星S与观测者O之间，忽略该过程中主恒星M与行星P相对位置变化，如图4，行星的引力场也会产生微弱的引力透镜效应，但是强度更弱，光变曲线在图3的基础上会有一个微小的变化，通过捕捉这种微小变化来搜寻系外行星.

图3 M产生的引力透镜效应

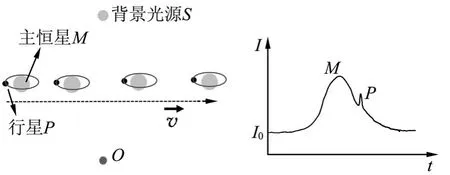
图4 恒星-行星系统的微引力透镜效应

3 模拟实验

3.1 制作透镜

接下来构建点质量天体对应的引力透镜，并利用3D打印机将透镜打印出来.设底面半径为r处透镜厚度为D（r），透镜的折射率为n，切线斜率满足，如图5（a），光线垂直于底面入射，空气折射率取1，根据斯涅耳定律有nsinβ=sin（α+β），α为入射角，β为折射角.当α，β为小角，则，积分得

其中B为积分常数，通过改变参数A，B调整透镜的厚度.笔者利用数学软件Mathematica11画出（6）式的三维图形，如图5（b），这里取B=50，A=3，r的取值范围为0.5～40，D（r）的取值范围为38～45，利用PlotTheme→ “FilledSurface”命令来填充曲面内部空间.为了使打印出的透镜表面更平滑，添加了PlotPoints→200命令，然后利用PrintOut3D命令将图形保存成3D打印机能够识别的STL文件格式.最后，笔者使用耗材为透明光敏树脂的3D打印机打印出两个尺寸的透镜（打印精度为0.1mm）.如图6，透镜L1的尺寸为15cm×15cm×1.3cm，透镜L2的尺寸为7cm×7cm×0.6cm.

图5 透镜示意图

图6 3D打印的透镜

3.2 模拟引力透镜效应

利用3D打印的透镜模拟引力透镜效应.将透镜L1固定在光具座的支架上，利用一个LED灯来模拟光源S，通过相机来拍摄S的像.将透镜中心、相机镜头和LED灯调整到同一高度，透镜放置于相机与光源之间，并尽量做到光线垂直入射透镜.在垂直于相机和光源的连线上移动透镜，从而改变透镜的位置.当光源、相机和透镜3者共线时，可看到爱因斯坦圆环；当3者不共线时出现两个像S1和S2，如图7，虚线表示爱因斯坦圆环所在的位置，可以看到像S1位于爱因斯坦圆环外侧，像S2位于爱因斯坦圆环内侧，且像S1比S2更明亮.

图7 （a）图为光源、相机和透镜共线时出现的爱因斯坦圆环；（b）图为三者不共线时出现的两个像S1和S2

3.3 模拟系外行星的搜寻

系外行星在移动过程中会引起背景光源亮度的涨落，我们利用手机软件Phyphox中的Light功能来测量亮度的变化.在相机的位置上放置手机，在垂直于手机与光源的方向上缓慢移动透镜L1，可以看到透镜扫过手机与光源连线过程中的亮度变化，如图8（a）.接下来，模拟系外行星的引力透镜效应，这里利用尺寸较大的L1透镜模拟主恒星M，小尺寸L2透镜来模拟行星P，将L2透镜固定在光具座的另一个支架上，靠近L1透镜并排放置（为简化问题，这里认为主恒星M与行星P相距较远，两者的引力透镜效应相对独立），并调整两透镜中心在同一高度，同时缓慢移动两个透镜，使得透镜L1、L2先后扫过手机与光源连线，我们看到亮度出现两个峰值，如图8（b）.用这个方法可以简便模拟恒星-行星系统的引力透镜效应.

图8 （a）图为透镜L1扫过手机与光源连线过程中的亮度变化；（b）图为透镜L1、L2先后扫过手机与光源连线亮度变化

4 结论

本文中，我们构建出符合点质量引力透镜效应的透镜模型，并用3D打印机打印出透镜.我们利用透镜来模拟了爱因斯坦圆环和源的成像，同时也模拟了系外行星的搜寻过程.该实验所需的器材简便易得，可以把天文图片中才能看到的现象变成有趣的研究性课程实践活动，学生在实验室中就可以模拟出天体的引力透镜效应.