关于“十字相乘法”的教学建议

白礼虎

摘要：新的课程标准虽然删除了“十字相乘法”，但是在实际教学中，很多初高中老师仍将其作为一个重要内容补充给学生，用以锻炼学生的思维和能力。鉴于此文中给出了四个教学片断，并对“十字相乘法”的教学给出了一些建议，以供参考。

关键词：十字相乘法;判别式;试误;教学

中图分类号：A 文献标识码：A 文章编号：（2022）-2-

整式乘法和因式分解是初中数学一个非常重要的内容，二者是一个互逆的过程。单就思维量而言，整式乘法要少一点，因式分解要复杂一些。文[1]中给出了十字相乘法的基本原理，同时对“十字相乘法”与“求根公式法”进行了比较，并且指出后者更具一般性，是适应性更宽的“通性通法”。新的课程标准《义务教育数学课程课标（2011年版）》认为“十字相乘法”不是一般方法，故而删去了“十字相乘法”。但是很多一线教师和学者对此不太赞同， 文[2] 中认为“十字相乘法”可以对学生进行素质教育，有利于培养学生的逆向思维和探索精神。文[3]中认为“十字相乘法”并未增加多少学生的学习负担，呼吁给“十字相乘法”留一席之地。文[4]中经过调查得出，初中数学教师在讲解因式分解过程中将其作为教学知识进行补充、高中数学教师在初高中知识衔接过程中将其作为教学知识进行补充是一个普遍现象.

本文就这一问题谈谈自己的认识，从“十字相乘法”的解题过程来看，将二次项和常數项分解后，交叉相乘再相加要等于一次项系数。问题的关键在于分解的不唯一性从而导致可能要多次尝试才能凑成中间的一次项系数。试误的过程加大了计算的难度，而且并不是所有的二次三项式都可以用，所以课本在因式分解一节中只介绍了提公因式法和公式法以及简单的分组分解法，对于“十字相乘法”只字未提。但是从实际教学角度来看很多教师倾向于添加“十字相乘法”作为补充内容。这主要是因为增加之后可以很好的锻炼学生的思维并巩固所学内容。学生一旦掌握，对于二次三项式的因式分解以及解一元二次方程和不等式都有更快速的解题优势。故而我认为尽管教材删除了，但我们仍然可以作为补充内容好好的讲解一下。那么究竟如何添加，讲解时要注意哪些要点，下面我给出四个教学片断供大家教学参考。

教学片断一：

问题：形如可以因式分解吗？

设计意图：在分组分解的基础上让学生掌握十字相乘法的一般原理。

教学片断二：

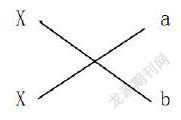
十字相乘法的形式：

举例：因式分解

一般形式：

其中，，

步骤：  1. 将常数项和二次项进行分解

交叉相乘和相加，凑成中间一次项

横写因式即可

简记为：竖向分解，交叉相乘，求和凑中，横写因式

规律：  1. 先将常数项分解成两个有理数的乘积，再看这两个有理数的和是否等于一次项的系数。

2. 当常数项为正数时，拆成的两个有理数一定同号，符号与一次项系数相同;当常数项是负数时，拆成的两个有理数异号，绝对值较大的数与一次项系数同号。

设计意图：让学生理解十字相乘法的格式，掌握常数项的分解规律。

教学反思：教学片断一、二是在因式分解中介绍提公因式法、公式法和分组分解法后紧跟着介绍“十字相乘法”。此时更多的以规律的形式给出，借助分组分解法，让学生掌握“十字相乘法”的一般原理，同时给出较简单的可以用“十字相乘法”的运算习题。第一课时注重对原理的理解，形式的把握，题目难度要严格控制。

教学片断三：

问题1：所有形如的式子都可以用“十字相乘法”吗？

举例：可以用“十字相乘法”吗？

让学生先来解一元二次方程，计算判别式

，

此时一定有两个根而且由于判别式不能开根，所以一定是两个无理根，此时不能用。

如果改成，可以吗？

问题2：你可以得出能用“十字相乘法”的判断标准吗？

结论：用判别式进行判定，如果可以开根，则可以用“十字相乘法”得到有理根。

设计意图：本节内容放在一元二次方程后面，进一步介绍“十字相乘法”的适用范围，给出了“十字相乘法”的一个判定标准，避免盲目试误。

教学片断四：

问题：可以用十字相乘法吗？如果可以，该怎么分解？

举例：因式分解

先算判别式，可以开根。

结论：当二次项系数不为1时，也可对其进行分解 。

一般形式：

其中，，，

设计意图：将“十字相乘法”进一步扩展到二次项系数不为1的情况，让学生更深刻体会它的形式和原理。

教学反思：教学片断三和四，作为第二课时要到二次函数和一元二次方程结束之后，进一步讨论“十字相乘法”。此时学生已对“十字相乘法”有了一定的了解，要着重从判别式的角度对该方法的适用情景做探讨，并且进一步将“十字相乘法”推广到二次项系数不为1的情况。

小结

文中以四个教学片断展示了“十字相乘法”教学的几个主要内容，即“十字相乘法”的原理，求解的过程，适用的判断方法以及推广到二次项系数不为1的情况。建议分两个课时从两个不同的时间段进行切入。第一个为初学阶段，重点为原理;第二个为深入阶段，重点为灵活运用。在第一个阶段，学生初次接触到“十字相乘法”，要引导学生逆向思考，注重学生的探索精神的培养。第二个阶段，学生已学习了二次函数以及一元二次方程的相关内容，特别是求根公式的使用，可以和学生讲解“求根公式法”和“十字相乘法”二者之间的联系，让学生灵活运用。

参考文献

[1]王尚志，张思明，胡凤娟.如何认识“十字相乘法”？（一）[J].中学数学教学参考，2008（11）：6-8.

[2]邝孔秀.“十字相乘法”该删吗？[J].数学通报，2001（10）：22-23.

[3]王怀喜.请给“十字相乘法”留一席之地[J].中小学数学（初中版），2013（Z1）：84.

[4]郭蕊. 初中数学“十字相乘法”教与学的调查研究[D].新疆师范大学，2016.