小近距隧道台阶法开挖爆破振动信号特征分析
2022-02-23任文斌付晓强
任文斌,付晓强,俞 缙
(1.中铁十二局集团第四工程有限公司,西安 710000;2.三明学院建筑工程学院,福建 三明 365004;3.华侨大学福建省隧道与城市地下空间工程技术研究中心,福建 厦门 361021)
随着城市化进程的加快和现代交通的发展,城市居民对出行便利性的要求越来越高,城市公路隧道建设日新月异。城市环境复杂性高,施工控制标准严格,钻爆法掘进过程中产生的冲击、振动等次生灾害对周围建(构)筑物的影响不容忽视。爆破振动监测作为爆破效果评估最为有效的手段之一,其监测信号的特征提取对指导高效安全施工具有积极的现实意义[1-2]。
针对于此,国内外科研院所和工程技术人员对复杂环境下隧道掘进采集数据开展了大量的研究,取得了丰硕的成果。如付晓强等[3]对青岛地铁3#线爆破监测信号中包含的趋势项等干扰成分进行了消除,提取得到了反映爆破特征的真实信号,有效地避免了信号“端点零漂”现象对信号特征的影响。汪平等[4]采用HHT方法对京张高铁地下车站开挖爆破信号进行了深入分析,得到了爆破主振频率范围,为构筑物保护提出了针对性的控爆措施。韦啸等[5]以乌鲁木齐轨道交通1#线掘进为背景,通过不同信号分解方法最终获得了可靠的信号波形,通过信号瞬时能量波动分析,科学把握了隧道掘进振动效应变化规律。上述及相关文献均为本文提供了极具价值的借鉴,然而受工程复杂性和测试条件的限制,隧道爆破信号特征提取仍面临诸多挑战,如信号分析精度差,求解效率低等关键性难题。
传统的信号分析方法在实现信号特征解析的同时,也存在一定的局限性。如王海龙等[6]通过隧道信号分析实践发现,小波分析方法中小波基的选取对于分析结果至关重要,同时,最优小波基的选取对分析人员的经验性要求较高,对分析者的先验水平依赖较大。郭云龙等[7]采用HHT方法对隧道爆破信号进行分析,证实了该方法的优良特性,也指出了其主要缺陷是信号分解过程中易出现模态混叠和端点效应,一定程度上影响了信号解析精度。吴义文等[8]通过经验小波变换对矿山微震信号和爆破振动信号进行了识别,收到了良好的效果,验证了该分析方法的高效性和优良解析能力。本文以厦门海沧疏港通道大跨度隧道钻爆法施工为背景,通过对隧道爆破信号进行有效监测和开展精细化特征提取,获得了隧道爆破时频能量变化特征,并对雷管实际起爆时刻进行了识别,为同类工程爆破信号分析及安全高效掘进提供了一定的理论参考。
1 算法基本理论
1.1 经验小波变换
经验模态分解(Empirical Mode Decomposition,EMD)和小波变换(Wavelet Transform,WT)均为经典的时频变换方法[9]。而经验小波变换(Empirical Wavelet Transform,EWT)是法国学者Gilles结合上述EMD分解的自适应性和WT分析理论而提出的,其根据信号的傅里叶频谱特征,自适应地选取小波滤波器组对目标信号的模态分量进行提取。
对于任意给定信号,其归一化的傅里叶特征频率区间为[0,2π]。根据香农采样定理,将傅里叶支撑频率[0,π]分成N个连续分段Λn=[ωn-1,ωn],ωn为各分段边界,则:
(1)
以每个ωn为中心,取宽度Tn=2τn作为过渡段,如图1所示。

图1 经验小波分解特征频率区间Fig.1 The characteristic frequency interval of empirical wavelet decomposition

(2)
(3)
式中:β为ω的函数,其常用表达式为[12]
β(ω)=ω4(35-84ω+70ω2-20ω3)
(4)
参数γ须同时满足以下两项条件[13]:
(5)
经验小波变换定义为各频率分段对应的带通滤波器,其关键是如何根据实际应用场景选择合适的频谱分割方法。简单可行的做法是根据信号频谱图并寻找幅值极大值点,按照递减顺序依次排列为(P1≥P2≥…≥PL),取PL+α(P1-PL)为阈值,通常α位于0.3~0.4区间内能获得最佳区分效果。在上述条件下,EWT的计算方法与传统小波类似,用IFFT表示傅里叶反变换,则细节系数定义为信号与经验小波函数的内积[14]:
(6)
式中:f(t)为输入待分析信号。近似系数定义为信号与经验尺度函数的内积:
(7)
根据上述EWT重构原理,输入信号可表示为低频趋势项分量、高频噪声和经验模态分量(Empirical Modes,EM)的叠加,即:
(8)
式中:f0(t)为信号中含有的趋势项;fn(t)为分解得到的第n阶EM分量;fw(t)为信号中的高频噪声。从输入信号中自适应地剔除信号中的趋势项干扰和高频噪声,便可获得重构后的信号[15]:
(9)
基于EWT分解为研究信号按时空滤波器分离和提取提供了依据。通过对分解后的各模态分量设定频率滤波器,可将信号趋势项和噪声模态分量直接滤除,从而获得更为真实的特征信号。
1.2 Hilbert时频谱
利用EWT变换,得到信号中包含的不同固有频率对应的经验模态分量。对有效模态分量进行希尔伯特变换并叠加,便提取得到了表征信号瞬时频率和瞬时幅值的Hilbert时频谱。信号f′(t)的Hilbert变换的定义为[16]
(10)
构造解析信号:
(11)
从上式可获得输入振动信号的时频分布为
(12)
2 爆破振动信号时频特征提取
2.1 信号采集与获取
厦门海沧疏港通道工程项目西接海新路-疏港通道互通工程,向东延伸,设蔡尖尾山1#隧道下穿蔡尖尾山,而后设新桥水库大桥跨越新桥水库和柯坑水库泄洪道,之后设蔡尖尾山2#隧道下穿蔡尖尾山,其间隧道设置海疏互通上跨芦澳路隧道后上跨新阳隧道(原海沧隧道),终点接在建的马青路吴冠互通,路线全长5.307 km,道路等级为城市快速路(结合一级公路),双向六车道,设计时速80 km/h。1#隧道全长120 m,通过新桥水库大桥与全长4 500 m的2#隧道相连,主线2#隧道与芦澳路主线隧道于新美路节点设置芦疏互通立交一座,两条主线隧道通过分岔形成互通关系。隧道左、右线及小间距分叉位置关系如图2所示。

图2 蔡尖尾山2#隧道及小间距分叉位置关系Fig.2 The relationship between Caijianweishan 2# tunnel and its small-spacing bifurcation
由于隧道周边有少许民房以及高压电塔,爆破施工对地表建筑物的振动及由此产生的不均匀沉降,会严重影响建(构)筑物的安全。同时,本工程具有大跨小间距特点,隧道分叉开口处中夹岩厚度仅为1.03 m。现有《爆破安全规程》(GB 6722-2014)中对于一般交通隧道爆破安全振速规定为:①主频f<10 Hz时,振速v为10~20 cm/s;②主频10 Hz

图3 台阶炮孔布置Fig.3 Blastholes arrangement of bench blasting
上台阶爆破掏槽孔采用二级复式掏槽形式,第一级掏槽孔6个,倾角75°,炮孔深度1.4 m,采用MS1段电雷管起爆,单孔装药量0.8 kg,同时在一级掏槽孔中部钻凿2个超深空孔;第二级掏槽孔6个,倾角85°,采用MS3段电雷管起爆,单孔装药量0.6 kg;掏槽部分总装药量8.4 kg。工作面布置3圈辅助孔,分别采用MS5、MS7和MS9段雷管跳段使用,避免峰值振动相互叠加,其中,MS5段布置12个炮孔,MS7段布置28个炮孔,MS9段布置21个炮孔,单孔装药量均为0.4 kg,辅助孔部分总装药量为24.4 kg。周边孔采用MS11段雷管,沿隧道开挖轮廓500 mm间隔共布设19个装药炮孔,单孔装药0.2 kg,装药孔间布置减振空孔,底孔孔数为24个,单孔装药量0.3 kg,周边孔和底孔总装药量12 kg。上台阶炮孔总数138个,总装药量45.7 kg。根据振动控制标准要求现场试爆确定隧道单循环进尺为1 m,施工期间根据掌子面超前地质预报情况对爆破参数作相应调整。
为了客观评价上台阶爆破产生的振动对分叉中夹岩稳定的影响,在先行隧道中距掌子面20 m处间隔10 m布设监测点(见图4)。由于隧道内施工环境较为恶劣,容易导致仪器误触发或致使信号中包含无法直接消除的干扰成分。因此,为了提高仪器测试数据的精度,通过膨胀螺钉将三向传感器通过角铁固定在衬砌表面。同时,为了避免测点频繁布设对测试信号的影响,定制保护箱和大容量锂电池供电,通过降压板将供电电压降低至仪器电压范围,实现爆破振动的不间断监测,很大程度上保证了测试数据的完整性。

图4 隧道监测点布置Fig.4 Layout of monitoring points in tunnel
监测采用TC-4850型智能爆破振动监测仪,设定采样频率10 kHz,仪器为外触发方式,触发幅值为0.1 cm/s。隧道分叉开口处测点(距离掌子面50 m,高度与上台阶掏槽孔平齐)监测到的上台阶爆破过程中的竖向振动波形曲线,其波峰值为1.254 cm/s,波谷值为1.342 cm/s,峰峰差值为2.596 cm/s。从波形曲线波动形态(见图5)可知:隧道爆破产生的强振往往来源于掏槽段,而总装药较大的周边孔部分反而振动较弱。这是因为掏槽段自由面单一,炸药利用率高,主要用于岩体破碎。而随着辅助孔顺利起爆,工作面槽腔体积不断扩大,周边孔起爆时自由面进一步增加,同时高段别雷管精度相对较低,间接形成了小型毫秒延时起爆网路,很大程度上降低了爆破振动峰值强度。现场在雷管段别丰富的条件下,应优先将周边孔和底孔选用不同段别雷管,进一步削弱爆破振动危害效应,也便于铲装机械的铲运排渣。
2.2 爆破振动信号时频能量特征分析
经验小波变换是通过对信号频谱进行自适应分割,构造合适的小波滤波器组,从而提取信号的不同调频-调幅成分[17-18]。采用经验小波变换对图5中信号进行频谱分割,结果如图6所示。根据尺度空间方法获得的截止点(频谱图中红色虚线对应的频率点)分割频谱,再根据频谱区间进行逆变换重构,最终信号被分解为15个具有明确物理意义的分量,具体波形如图7所示。

图6 信号频谱分割结果Fig.6 The segmentation result of signal spectrum

从图7可知,经验小波变换分解得到的IMF1波形特征明显且包含了原信号的大部分信息,IMF2分量中MS11段雷管起爆波形出现了缺失。IMF3分量具有典型的噪声特征,其余分量幅值显著降低且均位于同一数量级,为信号中的微幅波动干扰。因此,选用IMF1分量做为分析特征信号。
经验小波变换将信号中的有效成分从被污染的信号中成功分离,且能够将有效信息集中在有限的IMF分量中(通常为IMF1分量),避免了人为判别选取的过程。为了验证信号分解重构效果,这里分别采用小波方法和经验模态分解方法对图5中原始信号进行分解重构。其中,小波方法中选取db8小波基,分解到第8层(最小划分频带为1 000/(28)=3.906 25 Hz)。经验模态分解选择低于500 Hz以内的子信号进行重构,两者算法重构得到的信号波形如图8所示,可以发现,小波变换及经验模态分解重构结果较为相似且均存在明显的噪声干扰,经验小波变换重构信号波形平整光滑,杂波干扰被有效滤除,波形冗余度进一步降低并较好地继承了原信号的特征信息。
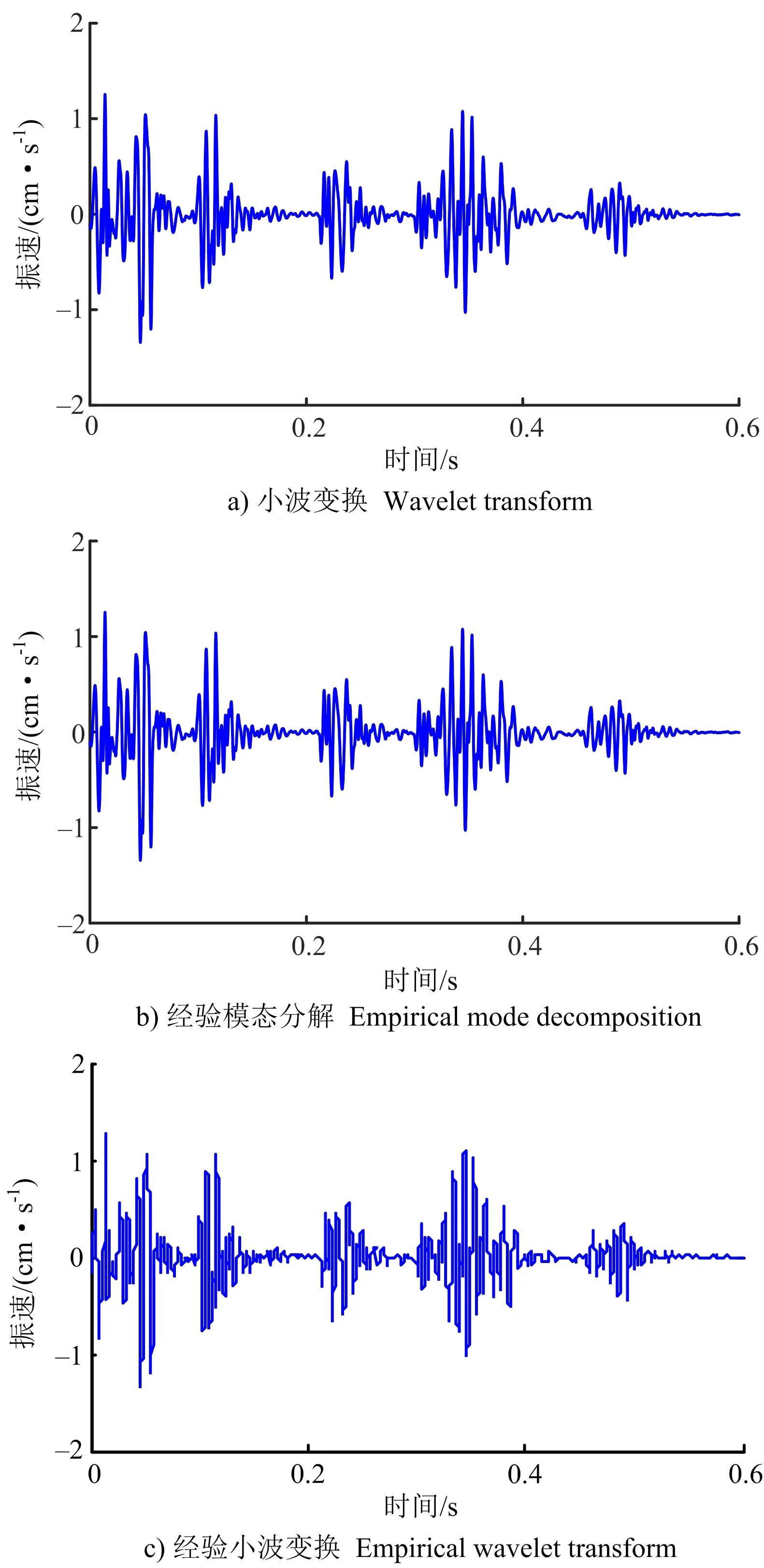
图8 不同方法重构特征信号波形Fig.8 Characteristic signal waveforms by different methods
为了提取特征信号和高频分量的时频分布,将图7中IMF2及其余分量线性叠加并求取其Hilbert谱(见图9a)。图8c特征信号的时频分布及细部如图9b及9c所示。特征信号Hilbert时频谱能在时间和频率两个维度对信号能量进行量化表征,其能量分布在频率轴上主要位于200 Hz以内,时间轴上与信号波动对应的峰值一致。信号优势频率位于96 Hz附近,这与图6中信号功率谱峰值对应的频率一致。时频图中各段别雷管起爆能量形态清晰可辨,隧道爆破信号时频谱出现了明显的能量聚集区域,分别对应不同段别雷管毫秒延时起爆时刻,体现了经验小波变换良好的时频表征能力和抗干扰特性。

图9 爆破信号时频谱Fig.9 The time frequency spectrum of blasting signal
为了揭示隧道爆破引起的岩体动态响应情况,这里,利用EWT对1 000 Hz以下的成分进行子频带细化分析。具体子频带构造方式为:500 Hz内每100 Hz划分为一个频率区间,500~1 000 Hz单独作为频带区间,这样便将1 000 Hz以内的信号成分划分为6个特征子频带,通过EWT重构得到每个子频带的重构信号(见图10)。

图10 不同频带信号重构结果Fig.10 The results of different frequency bands
爆破峰值振速可衡量爆破振动强度,常用于评价爆破危害等级。各子频带内,爆破峰值振速分别为:0.89、0.48、0.46、0.31、0.15、0.14 cm/s。说明随着频率的升高,振动幅值不断降低,两者呈现相反的变化趋势。
爆破信号的时频能量分布能够在时频域两个维度反映爆破作用特征,按照前述频带划分分别求取各子频带重构信号的归一化Hilbert能量谱(见图11)。从图11可知,对隧道岩体破坏起决定作用的频率主要集中在300 Hz以内,其中以优势频率所处的0~100 Hz范围区间尤为突出,子频带能量幅值与信号振速峰值表现为相同的变化规律,即随着振速峰值的降低,能量幅值逐渐降低并趋于稳定,体现了不同频带能量的贡献度。
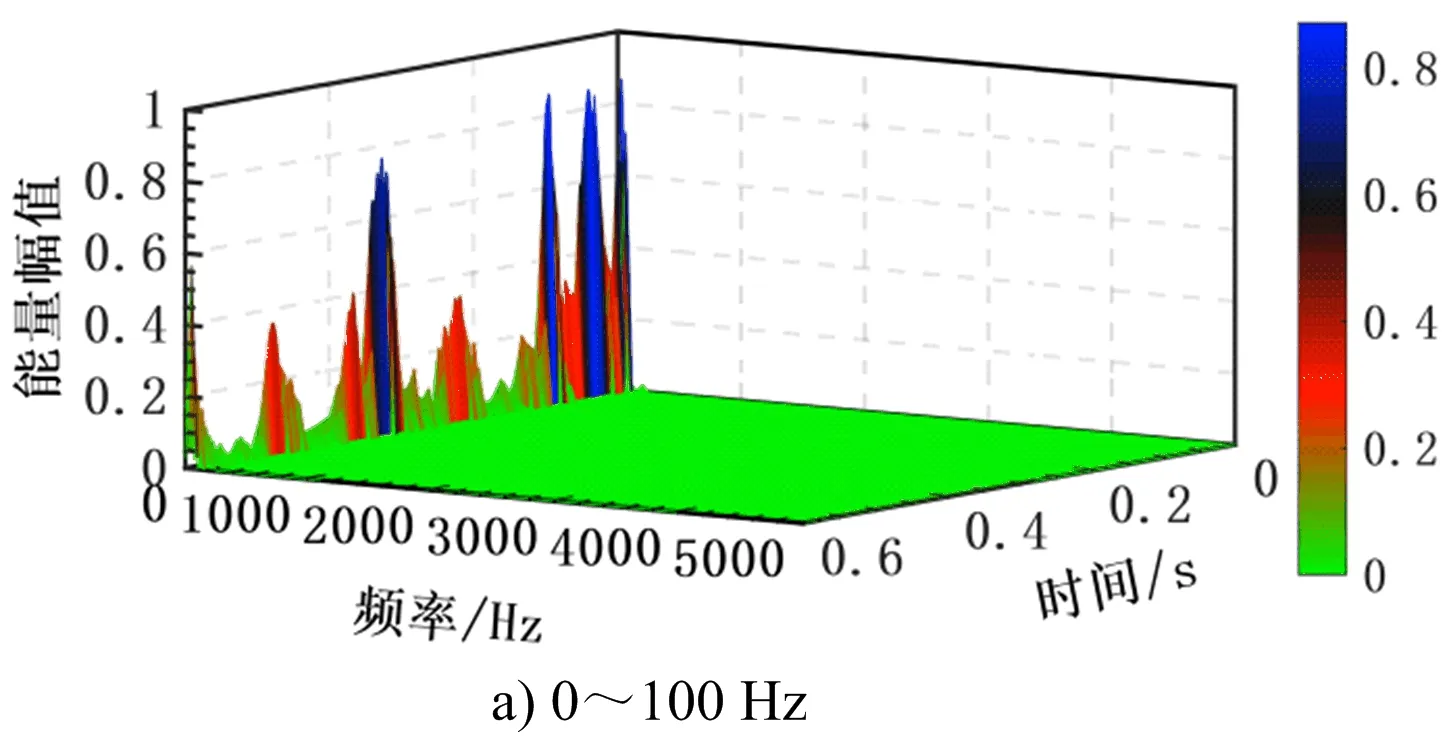

图11 不同频带信号时-频-能量分布 Fig.11 Time-frequency-energy distribution of signals in different frequency bands
图11充分表明隧道爆破信号属于更为宽频的非平稳随机振动,也体现了上述频带划分的合理性,从而揭示信号本身的固有特性。通常,频带子信号与原信号的相似程度可用相关性系数来定量描述,具体表达如下式:
F=CCF(s,xi,t)
(13)
式中:s为原信号,xi为各频带重构子信号,t为采样时间。
分别求取上述特征频率区间重构信号与原信号的相关性系数分别为0.73、0.42、0.36、0.22、0.15、0.10,说明随着频率的增大,子信号与原信号的相似性不断降低,对信号特征的继承度不断弱化。根据图11中能量分布结果并计算每个频带能量分布比重的均值,得到各子频带信号能量占比分别为53.41,17.69,17.18,4.80,2.33和1.13%,体现了随着频率的增大,子信号能量占比不断降低,与信号幅值和相关度变化具有统一性。为了探寻相关度与能量分布占比之间的关系,将两者绘制在同一曲线(见图12)。

注:子频带序列号与频带划分对应,1:0~100 Hz;2:100~200 Hz;3:200~300 Hz;4:300~400 Hz;5:400~500 Hz;6:500~1 000 Hz图12 相关系数与能量分布Fig.12 Correlation coefficient and energy distribution
从图12可以看出,相关性系数和能量百分比均随着信号频带增大而降低,表现为显著的正相关。说明按照上述频带划分可客观上把握信号的固有特征属性,从而揭示信号的能量与相关性变化趋势。同时,在后续的施工过程中,应持续监测并重点关注100 Hz以内频带能量的波动影响,保障隧道高效安全掘进。
3 隧道雷管起爆毫秒延时识别
经验模态分解由于存在明显的端点效应,使得各分量对其含有的噪声和干扰成分的变化极为敏感[19]。小波方法仍摆脱不了对小波基选取和分解层数的依赖,既无法深刻揭示因小波基选取不同而产生的背后算法导致的差异,也难以对信号频谱特征等关键问题进行探索。
根据文献[20]中方法并基于MATLAB平台编制程序,对图8中不同去噪方法获得的处理信号进行时—能密度雷管毫秒延时起爆时刻识别分析,结果如图13所示。

图13 不同处理方法时能密度曲线Fig.13 Energy density curve for different treatment methods
图13中A~F分别标识了隧道爆破所用MS1~MS11共6个段别雷管实际起爆时刻。不同信号处理方法获得时—能密度曲线均出现六个波峰值(奇异点),在时间轴上的位置分别为0.013 8、0.046 2、0.111 7、0.222 9、0.344 1、0.485 8和0.017 1、0.052 2、0.122 5、0.235 8、0.360 1、0.503 3以及0.008 2、0.046 2、0.109 8、0.216 4、0.334 9、0.483 5 s,段间毫秒延时时间间隔分别为32.4、65.5、111.2、121.2、141.7和35.1、70.3、113.3、124.3、143.2以及38、63.6、106.6、118.5、148.6 ms。分别将小波算法、经验模态分解和经验小波变换时能密度法得到的实际毫秒延时时间间隔与雷管标定设计延时时间间隔进行比较,结果如表1所示。
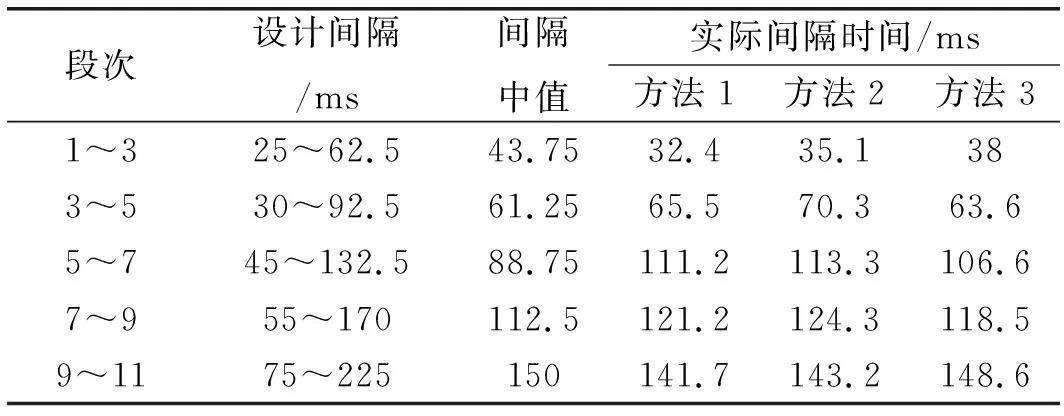
表1 不同方法雷管延时间隔识别结果
注:方法1为小波变换算法;方法2为经验模态分解算法;方法3为经验小波变换算法。段次1~3是指隧道所用雷管1段和3段之间的时间间隔,其他类似。
从表1中分析结果可知:随着雷管段别的增加,设计间隔逐渐增大,不同方法得到的特征信号的时能密度法识别效果均较为理想。通过表中数据对比不难看出,小波变换方法处理信号识别在MS1段雷管出现峰值干扰,导致1~3段识别间隔时间偏小,而经验模态分解处理信号在MS5段雷管亦出现峰值干扰,致使与MS5段雷管相关的3~5段识别间隔偏大,而5~7段间隔相对减小。经验小波变换方法重构信号各段别起爆峰值清晰突显,且识别得到的毫秒延时间隔与间隔中值误差最小,验证了该算法处理信号的精度和有效性。
4 结论
1)对于小净距大跨度隧道钻爆法施工掘进,应尽可能采用台阶法分部开挖形式,同时应采用短进尺、弱爆破、勤量测等辅助技术手段,最大程度降低隧道爆振危害。小净距大跨度隧道台阶法爆破开挖过程中,上台阶爆破开挖自由面单一,是隧道控制的关键部位。隧道爆破产生的强振往往来源于掏槽段起爆,这与自由面的数量、岩体夹制力和雷管毫秒延时时间有密切关系。
2)经验小波变换改进了小波方法的缺陷,具有精确分解信号的能力,对信号非线性变化的自适应能力强且运算效率高。隧道爆破信号各子频带信号峰值、能量百分比和相关性系数随频率增大表现为逐渐降低的趋势,三者变化具有高度的统一性。后续施工中要持续监测并重点关注100 Hz频带内能量的波动变化,保障隧道高效安全施工。
3)爆破信号中存在的干扰成分会很大程度上影响到雷管起爆时刻识别精度,经验小波变换识别得到的雷管与雷管出厂规定的延时区间中值最为接近。相较于传统的小波变换和经验模态分解算法,经验小波变换方法识别结果精度更好,可用于雷管精度的科学评估和爆破安全事故预防分析。
