下穿村庄隧道爆破振动效应研究

王海龙，柏皓博，王晟华

(1.河北省土木工程诊断、改造与抗灾重点实验室，河北省寒冷地区交通基础设施工程技术创新中心，河北 张家口 075000；2.北旺集团有限公司，河北 承德 067400；3.河北省装配式建造与地下工程技术创新中心，河北 承德 067400)

爆破施工技术在隧道工程领域得到广泛应用，而对于山岭隧道，目前最常用的施工方法为钻爆法。但爆破施工同时会带来一系列安全隐患问题，由于其突发性、破坏性强的性质，对临近建筑物的安全稳定性的影响不容忽视[1]。

建筑物破坏相关指标有速度、加速度、位移、能量等。由于质点振动速度最能代表对建筑物的影响，故国内外主要依靠质点振动速度峰值作为评价指标[2]。但实践证明，爆破振动危害与爆破振动速度、频率、持续时间息息相关，故须对爆破振动效应进行综合分析，综合考虑峰值振速与能量分布规律。小波包分析[3]作为一种新的时频分析方法被应用于非线性、非平稳信号领域，并取得良好效果，其可以将爆破振动信号在时域与频域上相互转换，进一步获取时间-频率-能量之间的联系。

目前，对于爆破振动的传播，一般采用萨道夫斯基公式来进行计算。方真刚等[4]利用量纲分析法，提出基于爆炸动力学的振动规律公式；宋光明等[5]对边坡爆破振动进行监测与分析，得到爆破振动在边坡上经验传播公式；唐海等[6]依托广东岭澳核电站爆破施工，通过量纲分析，得出反映高程放大效应的振速衰减公式；单仁亮等[7]通过进行室内冻结立井模型室内爆破实验，引入等效距离与等效药量，分析爆破振动时频特征；管晓明等[8]针对隧道爆破振动引起建筑结构损伤问题，对隧道爆破峰值振速和频率衰减规律进行阐述，总结得到结构振动损伤机理；陈经鹏等[9]将隧道挖空段的地表振动问题转化为半空间中的地表振动问题，得出隧道挖空段地表振速的计算方法；谢全民等[10]对某市地铁隧道爆破过程中周边建筑物进行振速监测，并利用小波分析对爆破振动信号时频特征进行分析，确保工程安全进行。

基于以上研究，本文依托太锡铁路太崇段新建崇礼隧道下穿和平村实际工程，引入等效距离、等效药量的概念，提出新的爆破振动衰减公式。对爆破振动进行实时监测，对爆破振速进行拟合分析，验证公式适用性。同时利用小波包对实测信号进行分析，探讨本工程爆破振动时域、频域与能量之间内在联系。

1 爆破振动衰减规律研究

从物理意义上来讲，振动速度可以代表幅值，而幅值和频率作为描述振动效应的最基本物理量，故爆破振速对于评价建(构)筑物安全性有着重要意义。目前，对于平整地形上爆破振动传播规律，一般采用萨道夫斯基公式[11]：

(1)

式中:v为爆破振速，cm/s；Q为单响最大装药量，kg；R为爆心距，m；K，α为爆破工程施工中的相关地质系数。

常规的萨道夫斯基公式通过单响最大药量与几何爆心距来预测爆破振动速度，忽略了爆破工程中分段爆破、以及不同炮孔爆破产生相互影响的实际情况。故引入等效药量以及等效距离的概念来进行计算。研究表明[12]，对于实际工程中分段起爆的实际情况，综合考虑不同段位炮孔起爆产生的相互影响，将雷管与传感器之间的距离采用等效距离进行衡量，最大单响药量取用等效药量：

(2)

(3)

式中：R′为等效距离，m；Q′为等效药量，kg；qi为同段第i个炮孔装药量，kg；ri为同段第i个炮孔距离传感器的距离，m。

则可以得到引入等效药量与等效距离的萨道夫斯基公式：

(4)

式中：K为与地质条件有关的系数，α为衰减系数。

1.1 工程概况

崇礼隧道位于河北省张家口市崇礼区西湾子镇，为单洞隧道，隧道起讫里程为DK62+310至DK67+800,全长5 490 m。DK65+500-DK65+800段，隧道洞身下穿崇礼区西湾子镇和平村。根据施工设计要求，本工程计划控制爆破振速为2 cm/s。新建隧道与断面如图1所示。本工程采用毫秒雷管，具体爆破参数如表1所示，炮孔布置如图2所示。

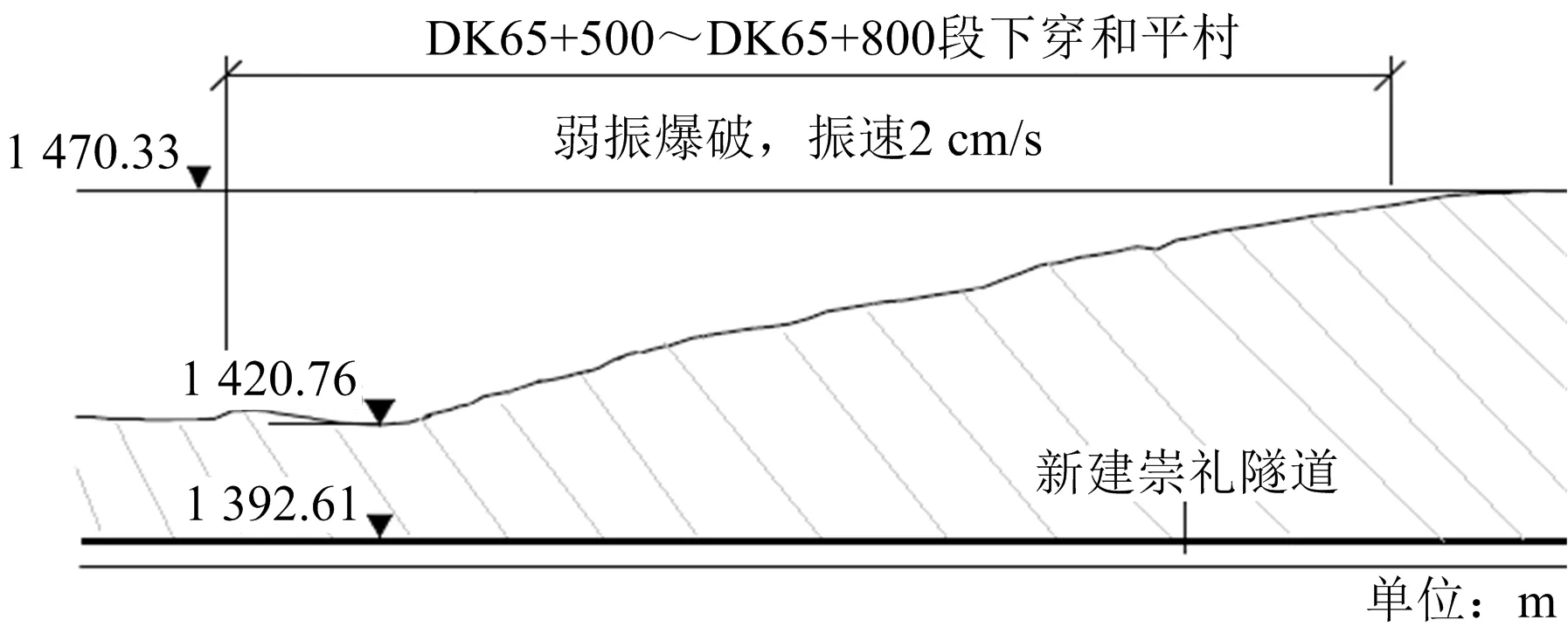
图1 隧道纵断面Fig.1 Longitudinal of tunnel

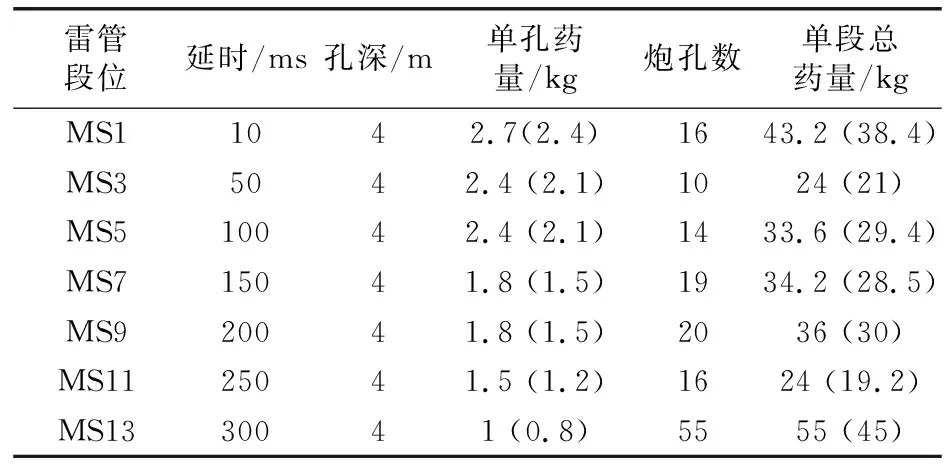
表1 爆破参数

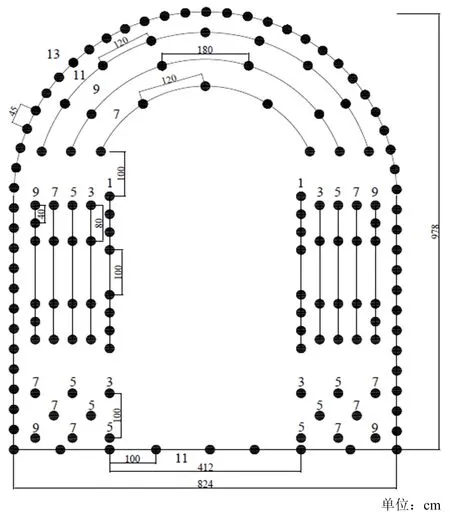
图2 炮孔布置Fig.2 Layout of blasting hole

1.2 爆破振动数据采集与分析

本次爆破监测设备采用M20爆破测振仪，该爆破测振仪配有三向传感器，令x方向指向隧道掘进方向，y方向指向隧道径向，z方向垂直于x方向、y方向垂直向上。通过激光测距仪确定位置后，利用不锈钢夹片将传感器固定于隧道边墙上。测点布置如图3所示。爆破振动数据如表2所示。

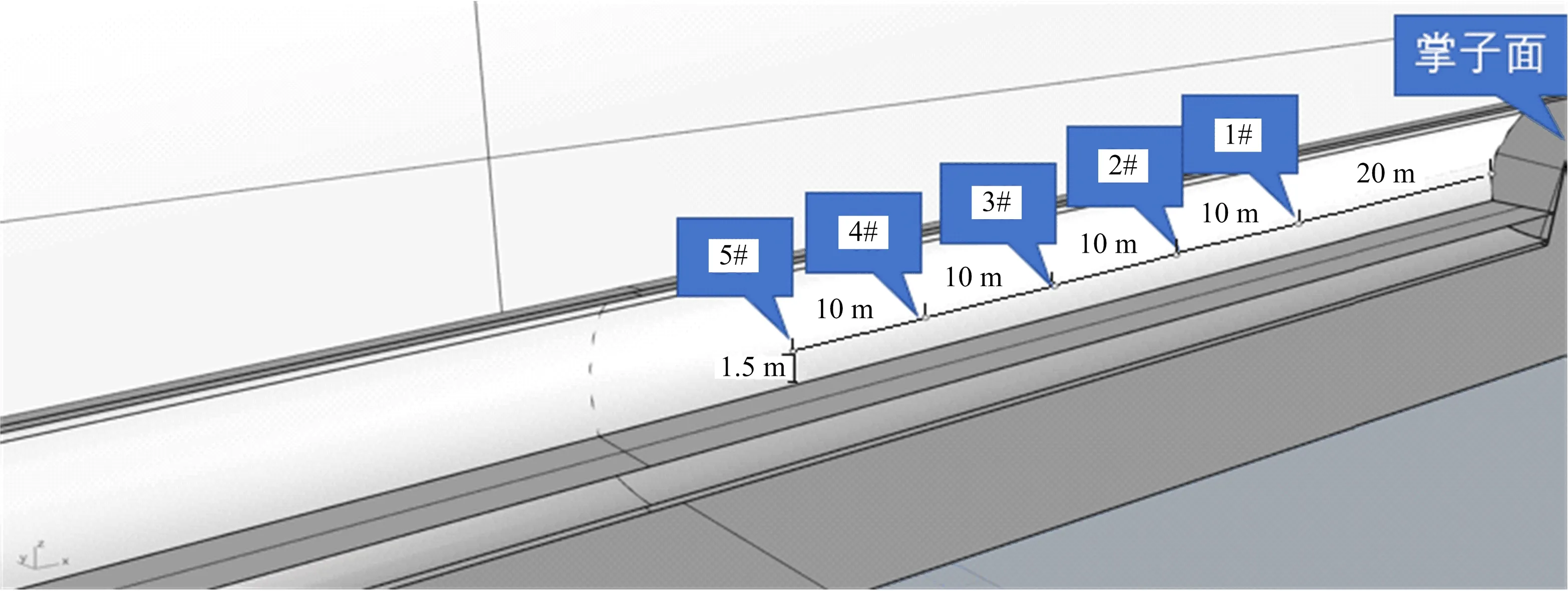
图3 测点布置Fig.3 Layout of measuring points

研究发现，爆破振动对临近建筑物的影响主要集中在垂直方向[13]，根据本工程监测所得数据，主要影响确为垂直方向，针对垂直方向振速进行拟合回归分析。

使用表2数据分别对萨道夫斯基公式与改进公式进行拟合回归分析，所得本工程振速预测公式分别为

(5)

(6)

计算所得萨道夫斯基公式相关系数R2为0.973 2，改进公式相关系数R2为0.986 3。根据两公式预测振速结果与实测数据对比如表3所示。

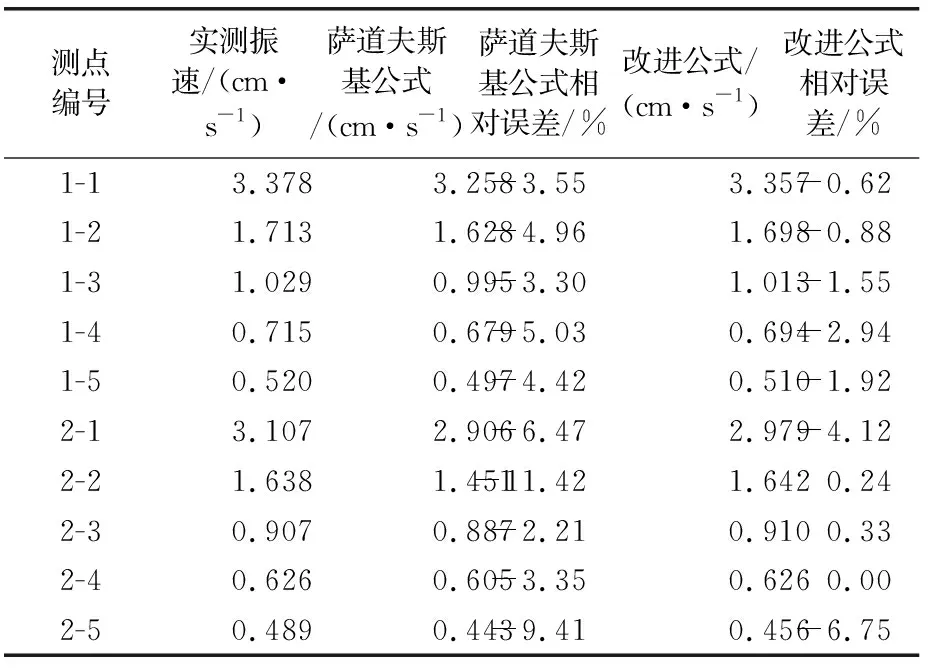
表3 拟合数据对比

式中：

(7)

可以发现，不同公式拟合所得相关地质参数K与α在进行振速预测时，所得结果差异较大，根据相关系数可知，改进公式拟合效果更好。利用等效距离与等效药量进行爆破振动速度预测，精度得到了显著提升。在本工程中，使用萨道夫斯基公式进行拟合，最大误差达到-11.42%，而改进公式预测振速最大误差为-6.75%，且一般误差均在1%左右。说明引入等效距离与等效药量的改进公式具有良好的适用性，可以为本工程提供精度较佳的爆破振动速度预测。在实际工程中，为保证爆破振速预测精度，应采用引入等效距离与等效药量的改进萨道夫斯基公式进行拟合，计算其相应爆破振速。

隧道与村庄最近等效距离为30.19 m，根据工程设计要求，最大爆破振速为2 cm/s，反算得到需控制最大单响等效药量为43.53 kg，对应最大单响药量为40 kg。

2 爆破振动能量衰减规律研究

2.1 小波包分析理论

小波包分解通过一组低通与高通滤波器将原始信号分解为高频和低频两个部分，选择最优小波基函数与分解层数对信号进行分解。其具体步骤为[14]：

1)定义正交尺度函数φ(x)以及其对应的小波函数ψ(x),设h(k)为低通滤波器系数，g(k)为高通滤波器系数，并且有h(k)和g(k)为共轭滤波器系数。

(8)

令μ0=φ(x)，μ1=ψ(x)，则

(9)

(10)

可得小波包分解算法为

(11)

对原始信号进行小波包分解后，得到n个不同频带的模态分量，所有分量能量总和应恒等于原始信号总能量。分别计算其不同分量能量占比，计算各频带分量能量占比[15]：

(12)

式中：Ei为分解所得第i个模态分量能量；E为信号总能量。

引入等效距离与等效药量，爆破振动能量衰减公式由下式表示[16]：

E′R′-3=K(Q′1/3/R′)α

(13)

式中：E′为振动能量；K、α为与地质条件相关的系数。

2.2 爆破振动信号的小波包分析

此次爆破测振仪采样频率为1 kHz，故Nyquist频率为500 Hz。选取“db8”小波基函数，对爆破振动信号进行5层分解，可得25个子频带，子频带宽为15.625 Hz。选取测点1～5数据进行代表分析。其振动速度时程如图4所示。

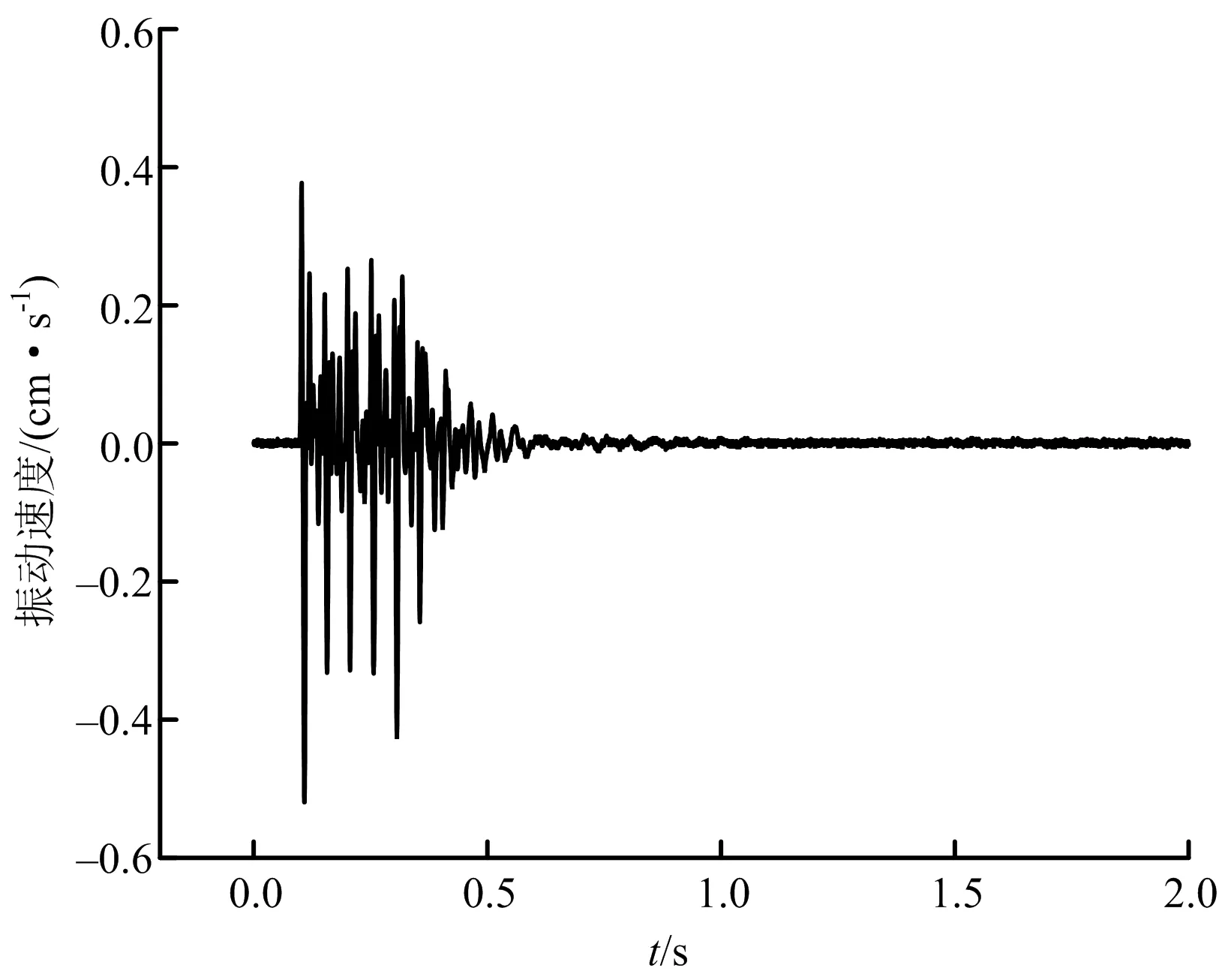
图4 爆破振动速度时程Fig.4 Time history of blasting vibration velocity

对此爆破振动信号进行小波包分析，求取其各个子频带对应能量占比，结果如图5所示。

图5 子频带所占能量百分比Fig.5 The percentage of energy in a subband

由图5可得，爆破振动能量集中于0～100 Hz，且主要位于0～62.5 Hz频率带上，故将频带再次划分为S1(0～15.625 Hz)、S2(15.625～31.25 Hz)、S3(31.25～46.875 Hz)、S4(46.875～62.5 Hz)、S5(62.5～78.125 Hz)、S6(78.125～93.75 Hz)、S7(93.75～109.375 Hz)、S8(109.375～500 Hz)。2次爆破监测所得振动信号能量占比如表4所示。

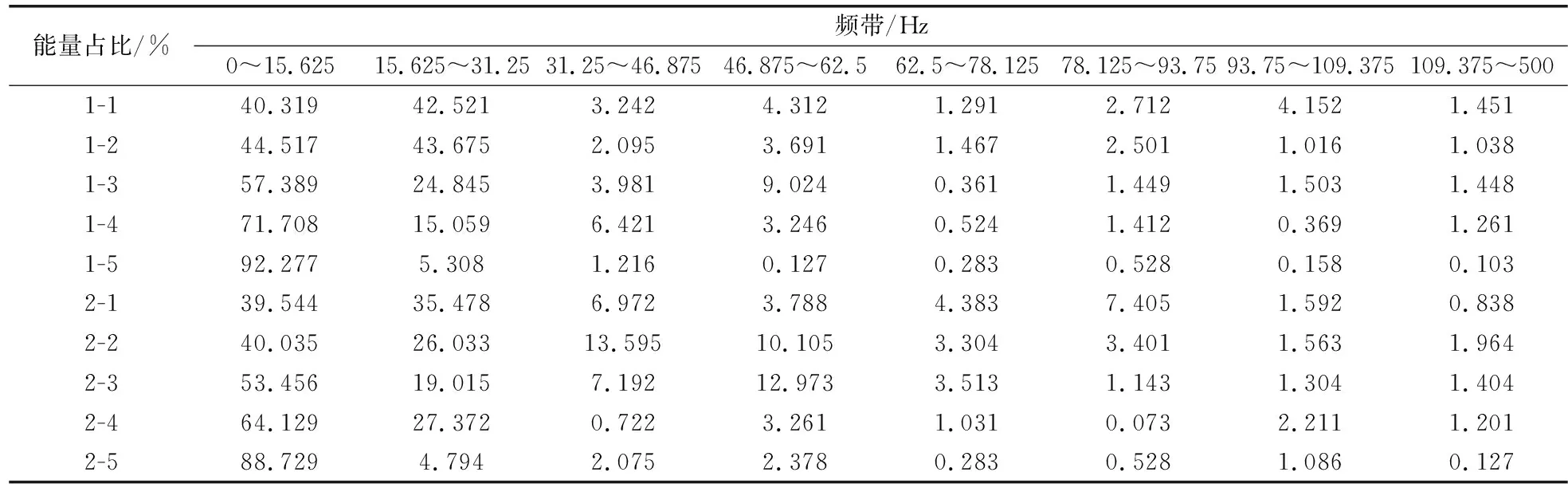
表4 爆破振动能量分布

取测点1-1、1-3、1-5、2-1进行代表分析，分别绘制不同爆心距与不同药量能量分布如图6所示。

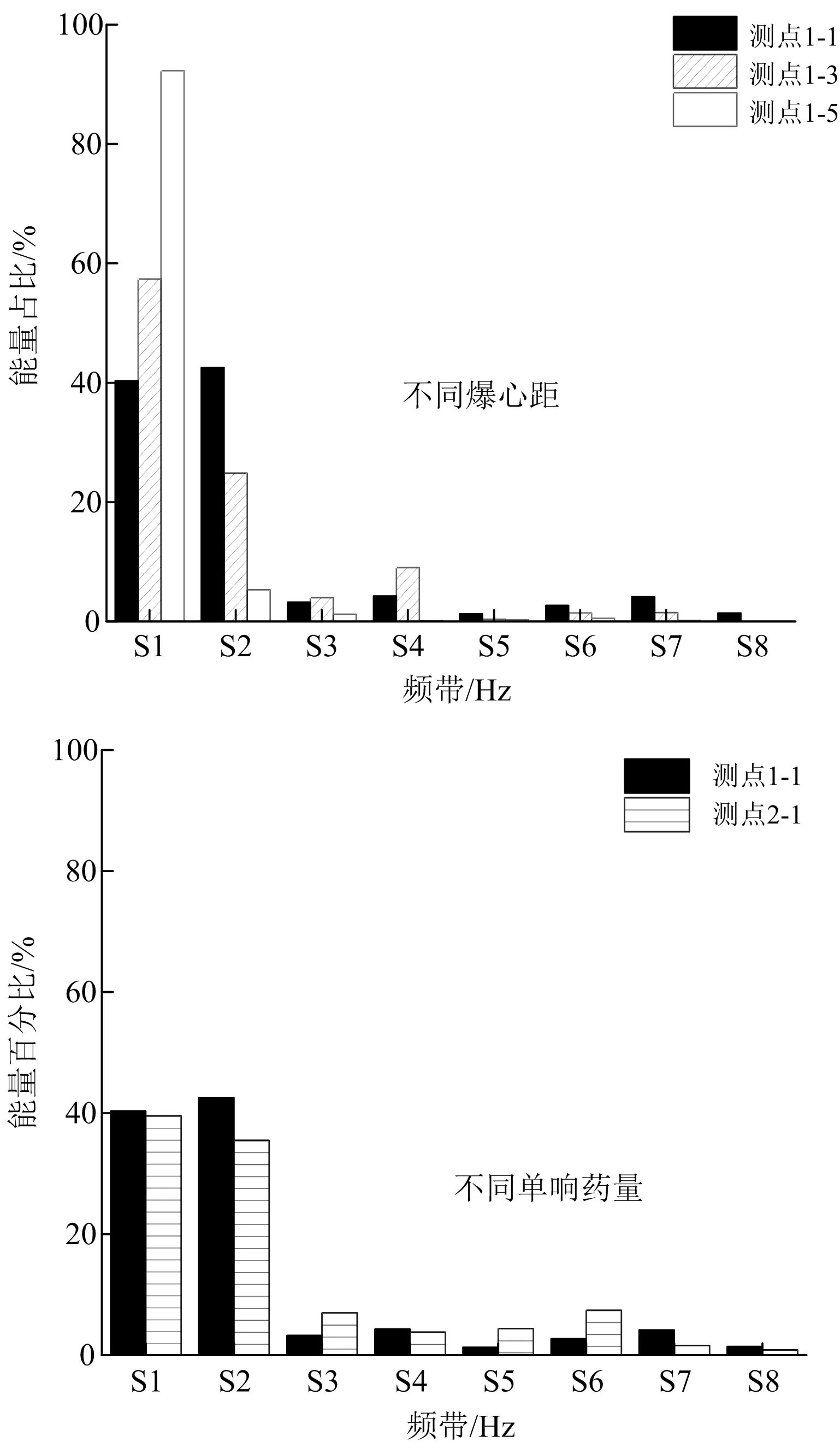
图6 能量分布Fig.6 Energy distribution

由表3与图6可得，随着爆心距的增加，信号低频部分(0～62.5 Hz)能量占比由90.394%(最大单响药量为55 kg)和85.782%(最大单响药量为45 kg)分别增加至98.928%和97.976%。这是由于爆破信号中高频部分主要为施工现场复杂工序交织进行而引起的噪声，随距离衰减很快，而爆破能量主要集中于信号的低频部分。同时，最大单响药量也在一定程度上影响信号低频能量占比。一般认为地面建(构)筑物自振频率位于10 Hz左右的低频，故在本工程施工时，应重点考虑爆破引起农村房屋共振问题，控制最大单响药量，避免共振问题的产生。

2.3 爆破振动能量衰减回归分析

取E′=E，利用表3相关数据对式(11)进行拟合回归分析，计算相关回归参数如表5所示。

表5 能量衰减公式回归系数

拟合后Z方向能量衰减规律可用下式表示：

(14)

由α>3可得，Z方向振动能量随等效距离衰减明显，E′与Q′、R′关系如图7所示。

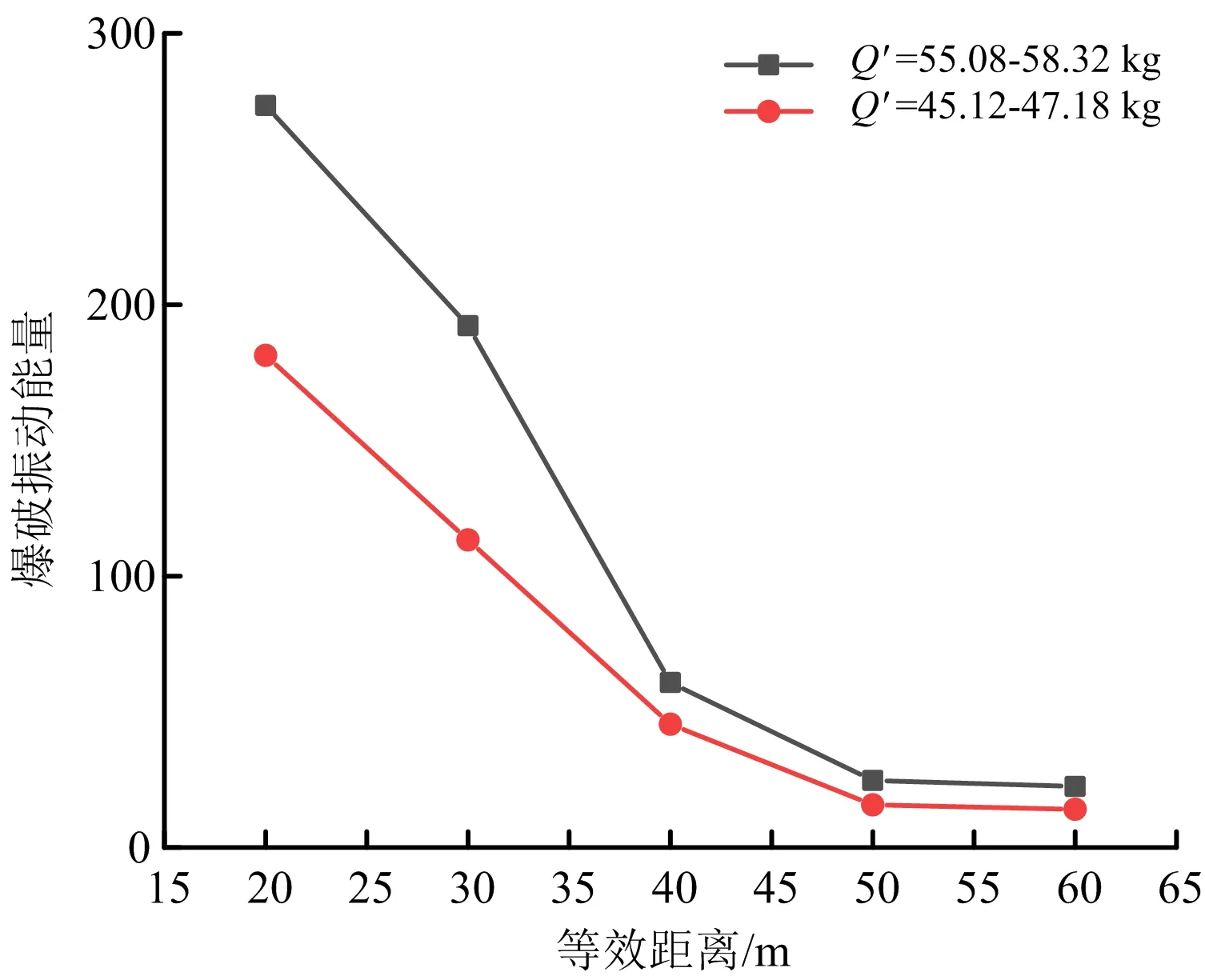
图7 能量E′与Q′、R′关系Fig.7 Relation between E′ and Q′, R′

由上图分析可得，当等效药量在小区间时，随着等效距离的增加，爆破振动能量衰减很快，尤其是在30～40 m范围内时，爆破能量急速衰减。等效距离30 m以内时，爆破振动能量较大，认为其为爆破近区；等效距离50 m以上时，可认为是爆破远区，此时爆破振动能量衰减趋于平缓。在本工程中，隧道中线距和平村房屋最近处为30 m，大部分距离为50 m左右，而爆破振动能量在50 m处已大量消散，这对保护村庄房屋安全是极为有利的。

3 结论

1)引入等效药量与等效距离改进萨道夫斯基公式，传统萨道夫斯基公式最大相对误差为-11.42%，改进后公式最大相对误差为-6.75%。通过改进公式反算得到距离村庄房屋30 m时，最大单响药量不得超过40 kg。

2)爆破振动能量主要集中于0～62.5 Hz，且随等效药量和等效距离的增加，该区间能量占比逐步增加。

3)对能量衰减公式进行回归分析，利用实测数据证明其正确性。等效距离40m内时，爆破振动能量急速衰减，50 m以上时，能量衰减趋于平缓。