三维点云特征的工件识别与位姿估计

张 铁，肖 卓，邹焱飚，何英武

（1.华南理工大学机械与汽车工程学院，广东 广州 510640；2.广州数控设备有限公司，广东 广州 510000）

1 引言

随着机器人技术的发展，工业机器人逐渐应用于工业生产中的自动抓取及装配中，需要对目标工件进行识别与位姿估计。工件的正确识别和准确的位姿估计都会影响工业生产的效率。因此，对工件的识别和位姿估计的研究具有重要的工程意义。基于图像的物体识别与位姿估计已经有很多研究成果［1］，文献［2］提出了一种基于区域划分的平面工件识别与定位方法，该方法先利用LSD（Line Segment Detector）进行直线段的提取，然后将干扰的杂线段分类进行剔除，在保留的轮廓线段基础上进行直线段的连接和区域划分，最后利用各个区域的形状特征向量和模板的形状特征向量进行比对，完成工件的识别和定位。但是，图像特征受到纹理、颜色、层次区分度、以及光照、分辨率、反射等外界环境的影响无法满足现代工业要求。而通过三维扫描仪获取3D点云数据已经非常便捷，将三维点云与位姿已知的模板点云进行匹配得到两者之间的刚性变换，从而实现工件的识别和定位，成为位姿估计领域的研究热点。

已有的三维点云工件识别与位姿估计方法是通过分析提取物体的特征点的几何属性、形状属性、结构属性等特征进行比对、学习从而完成物体的识别。基于描述子的识别方法随着描述子性能提升而不断提高［3］，文献［4］建立了定向点对特征的全局描述符，结合投票机制进行工件的识别与姿态估计；文献［5］提出依靠欧几里德距离评估特征描述符之间的相似性，训练卷积神经网络计算在描述符之间的相似性和差异性来计算描述符虽然该方法可以有效地捕获对象标识和三维姿态，但其对3D物体识别的效果较差；文献［6］给出一种随机森林随机抓取的位姿定位方法，提出立方体特征（CF）和基于段特征对（PSF）建立配对关系，采用随机森林算法实现模板点云和场景点云对应关系查找；文献［7］利用kinect采集到的深度信息及颜色与点云形状特征实现目标的识别与定位；文献［8］提出一种基于三维CAD模型生成测量对象点云数据库，通过投票法识别并估计不同物体的6自由度姿态的方法。

综上所述，这里针对存在干扰、目标遮挡、无纹理工件的场景中三维目标识别和姿态估计的问题，提出基于改进矢量构造的点云描述符SHOT（Signature of Histogram of Orientation），在估计点云法矢时将领域点距离信息考虑在内，构建工件点云特征；利用3D霍夫投票机制完成工件的识别，降低了错误的匹配概率；采用ICP（Iterative Closest Point）算法对点云进行精配准；实验中，采用离线建立某一姿态下的模板点云特征描述库，从不同的视角通过三维扫描仪获取真实的场景点云，识别目标工件，计算其相对于模板点云的位姿。这里采用的模板点云特征匹配的目标识别及位姿估计的算法流程图，如图1所示。

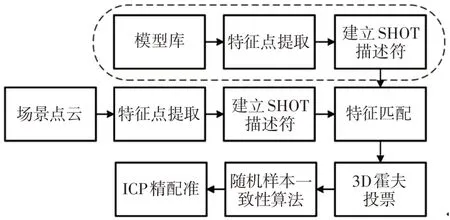
图1 3D物体识别与位姿估计框图Fig.1 Block Diagrams for 3D Object Recognition and Pose Estimation

2 基于点云特征的识别

2.1 特征点提取

特征点提取是在整个流程图中对模型点云和场景点云处理的第一步，对场景点云和模板点云采用统一重采样，即通过建立点云的空间体素栅格进行下采样，然后用每个体素内的重心代表该体素内的特征点F。

式中：n—点云中点的个数；(qxi，qyi，qzi)—每个点的沿x、y、z轴的坐标值。

2.2 点云法矢估计

对三维点云数据提取特征点后，以每个特征点的球形支持域内的局部坐标系建立SHOT描述符，因此建立局部坐标系需要具备唯一描述性和鲁棒性，建立局部坐标系的过程如下，主要分为2步：

（1）由特征点F的k个最近邻域点集P={pi，i=1，2...k}，建立协方差矩阵M，

式中：pi—k邻域中的第i个点；p^—点集的质心

对M进行特征值分解，采用总体最小二乘法估计法线方向。为了减小计算量，将（2）中的质心替换为特征点。为了提高局部坐标系在杂乱场景中的可重复性，给较远的点分配较小的权重，依次计算加权协方差矩阵M，可得：

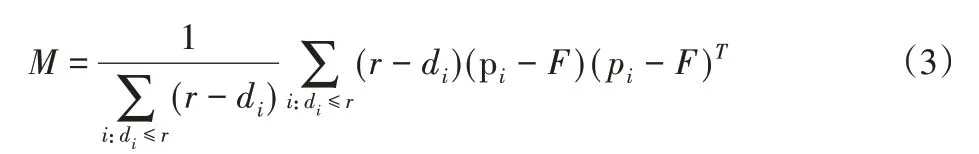
式中：di=‖pi-F‖2—点pi与F之间的欧几里德距离；

r—球面领域的半径。

此时，求得加权协方差矩阵M特征向量即为局部坐标系的三个单位向量。

（2）由于特征值分解法给出的特征向量的符号定义不明确，为了实现局部坐标系的唯一性，对式（3）中的特征向量采用符号一致性的方法消除歧义，将最大和最小特征值及对应的特征向量分别定义为局部坐标系x轴和z轴的单位向量，则消除歧义的x轴定义为：

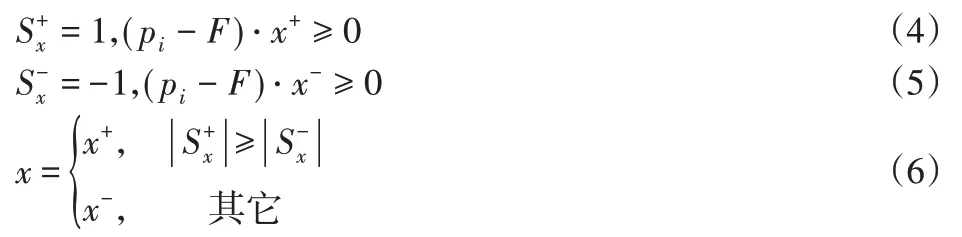
式中：x+—x轴的正半轴方向；x-—x轴的负半轴方向。

使用相同的过程消除z轴的歧义，最后y轴通过标准正交约束下的叉乘得到：

2.3 SHOT点云特征描述

（1）在特征点F处的r半径球邻域内建立局部坐标系，对球邻域沿径向、方位角方向、仰角等三个方向划分空间网格，其中，2个径向区，8个方位角区，2个仰角区，共分为32个空间区域，如图2所示。

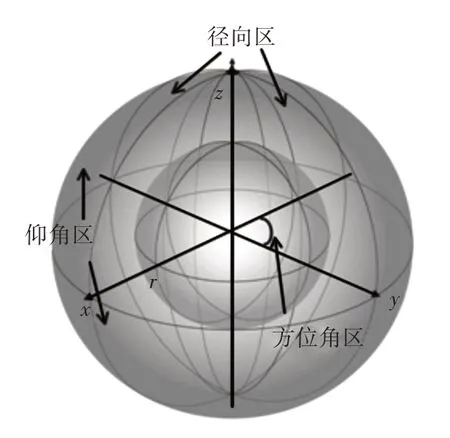
图2 SHOT描述符的特征结构Fig.2 Signature Structure for SHOT

（2）对于每个区域由局部直方图表示，每个直方图分为11个小单元，各单元的值根据网格中相应部分的每个点的法线nvi与特征点法线nu之间的夹角θi余弦值来累计点数而构建，即：

最终SHOT描述符的维度为32×11=352。根据局部坐标系将所有直方图有序地并排在一起。由于球形域上的空间细分，每个区域构建的单个直方图组合在一起会产生边界突变效应。另外在局部坐标系的扰动下，也会产生边界效应。因此，对于每个点累计到特定的局部直方图的单元格中，采用四次线性插值法，即对局部直方图中相邻的单元格和相邻直方图同一单元格内进行插值［9］。每个计数乘以每个维度的权重1-d，对于法矢夹角余弦的直方图相邻单元格插值，如图3所示。d的定义如式（9）所示，在方位角方向、仰角方向和径向方向插值类似。

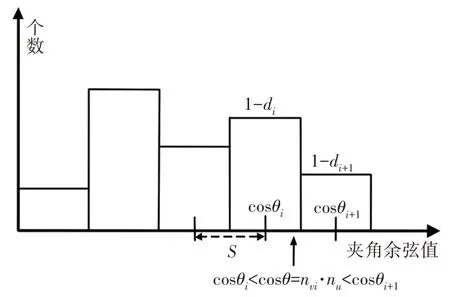
图3 法矢夹角余弦插值Fig.3 Interpolation on Normal Cosines

式中：s—相邻单元格间距。

3 特征点对的对应分组

为当前场景和库中的模板计算出描述符之后，通过kd树关联描述符空间中接近的模型－场景描述符对确定点对点的对应关系结果，如图4所示。蓝色圆圈表示特征点，虚线左边表示模型点云，右边表示场景点云。在三维物体识别中，通过加强几何一致性来消除伪对应，即特征点对的对应分组。

图4 配对关系（3D绿线表示正确的匹配，红线表示伪对应）Fig.4 Pairing Relationship（Green Lines Identify Correct Matches and Red Ones Represent Wrong Correspondences）

采用类似于［10］中提出的方法去除伪对应，在三维空间中，利用模型点云与当前场景点云之间的对应关系，通过局部坐标系将每个场景特征点与模型质心的相对位置相关联，使得每个对应的场景特征可以在三维霍夫空间中进行投票，足够多的票数来支持工件在三维空间中给定位置的存在，如图5所示。

图5 引入局部参考系的坐标变换Fig.5 The Coordinate Transformation by the Introduce of Local Reference Frame

在图5中，模型特征点为，场景特征点为，模型点云和场景点云的质心分别为CM，CS，CM和之间的向量表示为：

为保证向量在不同坐标系下具有旋转平移不变性，将向量转化到局部参考系（即为特征点坐标系）中，通过以下变换：

于是，每个特征点与其对应的向量关联在一起，对每对场景特征点与模型特征点建立的联系（↔），由于局部参考系的旋转平移不变性，所以有=。将转换到场景的全局参考系中，可得：

根据这些转换关系，场景特征点通过向量在3D霍夫空间中投票，在霍夫参数空间中，峰值的存在表明场景中存在目标。

4 基于ICP算法的点云精确配准

随机样本一致性算法［11］提供初始的场景点云相对于模板点云的变换矩阵，把变换矩阵应用于模型点云中，缩小两幅点云之间的旋转和平移错位，提高精确配准的效率和趋向，为了进一步提高配准精度，采用ICP算法［12］进一步优化，其实现的主要步骤为：

（1）场景点云S={pi，i=1，2…ns}表示目标点云，模型点云M={qi，i=1，2...nm}表示源点云，ns、nm分别表示两幅点云的规模。

（2）在M中选取一定数量的点qi，k，在S中寻找最近点pi，k，确定初始最近对应点集(pik，qik)；

（3）计算两幅点云之间的旋转矩阵R和平移矩阵T；

（4）计算转换后的源点云与目标点云之间的均方误差函数：

（5）当均方误差低于预先设定的阀值τ时，终止迭代，当前的R和T为最终的配准矩阵。否则更新配准变换后的点集pi，k，继续（2）、（3）、（4）的步骤，直到满足阈值要求。k表示迭代次数，N表示随机选取点集中的元素个数。

5 场景点云相对模型点云的位姿估计

位姿估计通过平移向量和旋转矩阵表示，旋转矩阵的表达又包括2种方式，即欧拉角和四元数［13］。设最终的变换矩阵为：

T=[t1t2t3]T—平移向量。

则场景点云坐标系下和模型点云坐标系下的六自由度位姿估计为：

对应的四元数为q=[q0q1q2q3]，其中；

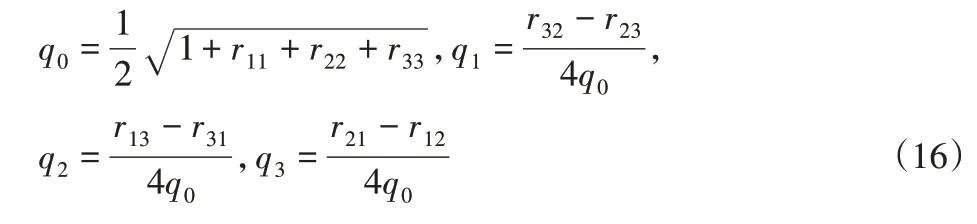
建立机器人视觉系统的坐标转换关系，如图6所示。机器人采用基于模板点云配准的方法获取工件位姿，引导工业机器人抓取工件，具体的变换矩阵如下式：

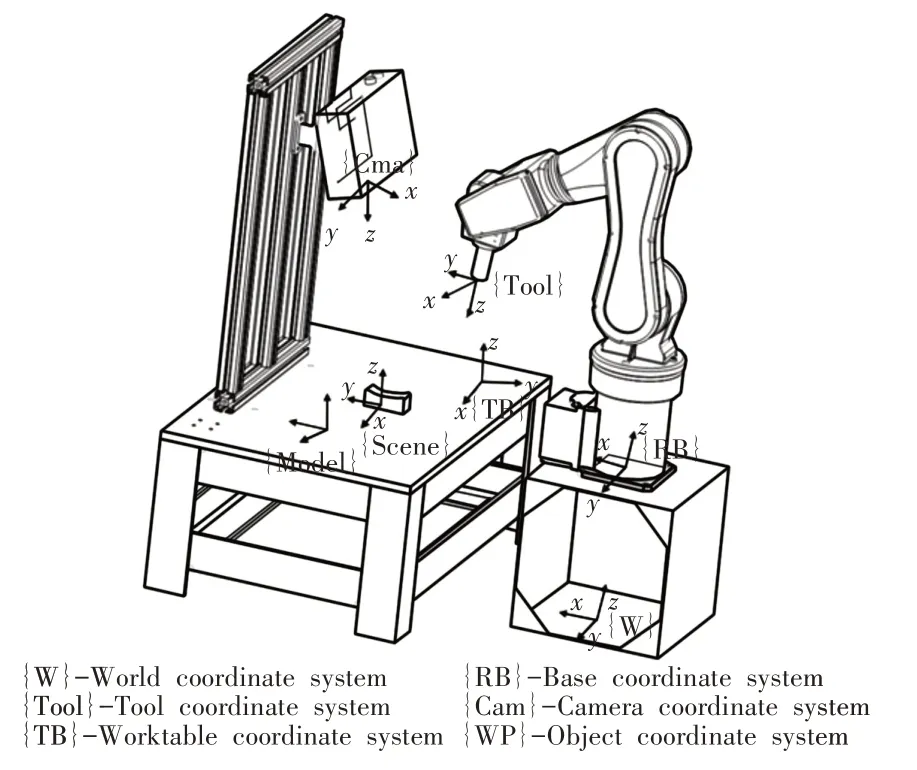
图6 Eye-to-Hand机器人系统各坐标系关系Fig.6 The Relationship Between the Coordinate Systems of the Eye-to-Hand Robot System

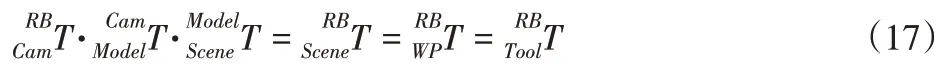
6 实验结果与分析

为验证方法的有效性，实验使用三维扫描仪获取曲面工件的点云数据进行实验，点云数据中包括点的三维坐标（x，y，z）和强度信息（intensity），点云分辨率为2064×1544。工件设计图和实物图，如图7（a）、图7（b）所示，实验平台，如图7（c）所示。

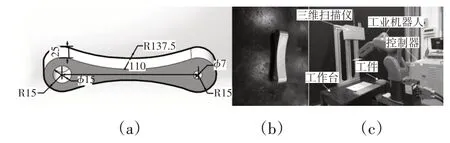
图7 工件设计图、工件实物图、实验平台示意图Fig.7 Workpiece Design Drawing，Physical Drawing of Workpiece，Experiment Platform

使用三维扫描仪采集单个工件点云，并对其进行处理得到红色表示的模板点云，如图8所示。同样得到黄色表示的场景点云，如图9所示。其中，对工件没有遮挡，工件放置于不同的位姿下，如图9（a）、图9（c）所示。对工件有部分遮挡的情况，如图9（b）所示。工件分别与其他物体相互接触，呈现不同程度的遮挡以及噪声，如图9（f）～图9（h）所示。为了提高计算效率，采用RANSAC算法拟合场景中的平面点云模型，分割出平面点云，去除背景点、离群点，得到最终匹配的场景点云，如图10所示。

图8 建立的模型点云Fig.8 Template Point Cloud

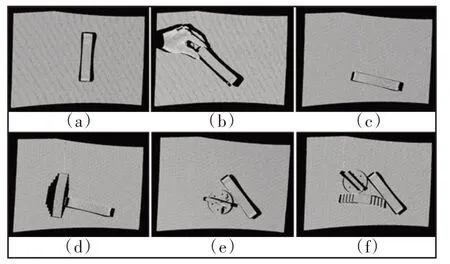
图9 原始场景点云图Fig.9 Original Scene Point Cloud

图10 预处理后的场景点云Fig.10 Preprocessed Scene Point Cloud

将获取的场景点云和模板点云进行实验，根据经验将相关参数设置为：对模型点云和场景点云分别使用宽度为10mm和30mm的三维体素化进行特征点采样。对于点法线的计算，取周围10个点计算法线；为特征点建立描述符的邻域搜索半径20mm；设置初始匹配的平方距离为0.25；局部参考系的半径设置为15mm；3D霍夫投票空间中，设置每个bin的大小为0.4，阀值设置为5.0。为了直观判断在场景点云中识别出工件的识别结果，将基于SHOT描述符的场景点云和模板点云的匹配结果进行可视化显示表示，如图11所示。绿色实线表示场景点云和模板点云建立特征点对应关系的对应对，浅黄色的点云表示模板点云在三维空间中的初始位置，红色点云表示根据随机样本一致性算法得到的初始位姿转换后的模板点云位姿。可以看到，场景点云（a～f）均与模板点云建立了正确的配对关系，表明采用到的场景点云中的工件实例均被正确识别。对场景点云（a～f）进一步采用ICP算法优化位姿关系，在ICP算法中，最大迭代次数为100次，两次转换之间的差值设为1e－6，配准效果，如图12所示。可以看到模型与场景点云基本准确配合。

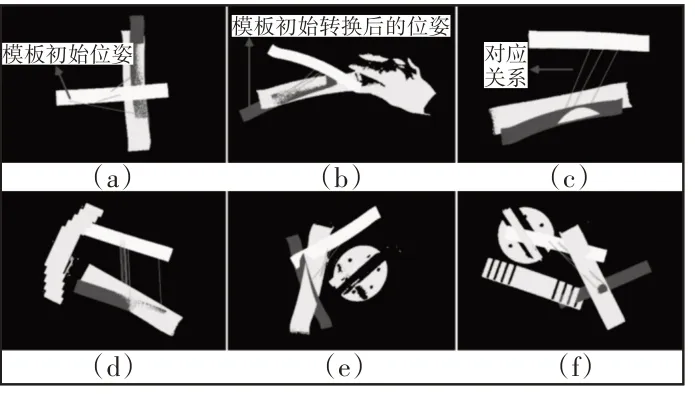
图11 3D对象场景中匹配局部描述符的结果Fig.11 Results of Matching Local Description in 3D Object Recognition Scenario

图12 这里方法的最终结果配准结果Fig.12 ICP Algorithm Registration Results

对于图12（a）所示的场景中，利用随机样本一致性算法得到模型点云与场景点云之间的初始位姿关系及利用ICP算法进一步精配准得到两者间的位姿关系，两者的乘积得到原始场景点云中的工件实例相对于模板点云的位姿转换关系：

代入式（15）、式（16）将变换矩阵转化为6自由度以及四元数表示形式：

利用两组点云间的欧几里德距离平方误差的总和评估两组点云的配准精度，配准误差，如表1所示。表中第一行表示这里方法最终的配准，第二行表示单独使用ICP算法的配准精度，单独采用ICP算法的配准效果，如图13所示。结果表明在精确配准前加入初始配准可以得到好的配准效果，使用这里方法的配准精度远远优于单独使用ICP算法。在实验中，所采集到的场景点云中的工件实体均被正确识别，总的识别率为1。

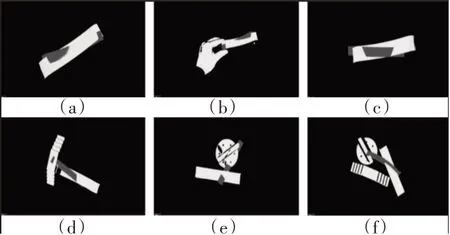
图13 单独采用ICP算法的配准结果Fig.13 Registration Result Using ICP Algorithm Alone

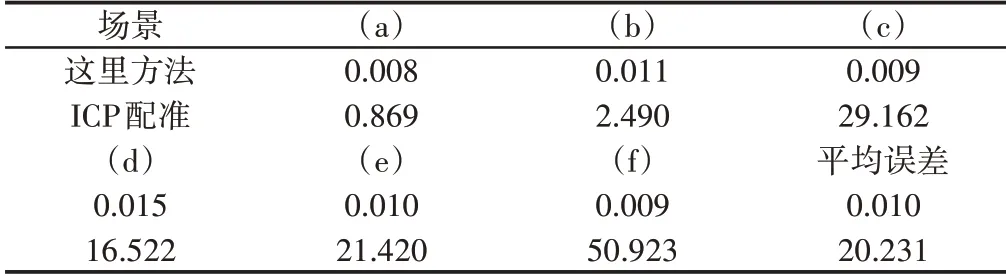
表1 配准误差（mm）Tab.1 Registration Errors（mm）

7 结论

为实现工业机器人能够在复杂的环境中准确高效地识别和定位工件，提出了基于点云特征的方法进行了目标工件的识别和定位，改进局部坐标系的建立方法，SHOT描述符结合了特征和直方图，具有更好的鲁棒性；根据向量之间的关系，使用3D霍夫投票机制完成对工件的识别，最后利用了ICP算法精细化位姿。最后通过三维扫描仪采集的点云数据进行实验，结果表明：基于特征点建立SHOT三维局部描述符的识别配准以及ICP精配准算法能够准确识别工件，并且获得比较高的配准精度，配准平均精度为0.010mm，从点云的转换图像中，可以看到模型点云与场景点云两者间具有比较好的拟合效果，说明了方法的可行性。在许多机器人场景和应用中，基于三维点云的形状特征为准确识别并估计目标物体的位姿提供了解决方案，丰富了工业机器人利用三维点云对物体位姿估计的方法。