超磁致伸缩驱动器磁路设计与仿真

闫洪波，高 鸿，牛 禹，郝宏波

（1.内蒙古科技大学机械工程学院，内蒙古 包头 014010；2.包头稀土院，内蒙古 包头 014030）

1 引言

超磁致伸缩材料（Giant Magnetostrictive Materials简称GMM）作为一种新型功能材料，被广泛应用于传感器、驱动伺服阀、精密微位移驱动、机械振动等领域[1-4]。超磁致伸缩驱动器（Giant Magnetostrictive Actuator简称GMA）是以GMM棒为核心元件，设计能够实现机械能－磁场能－电能之间转换的器件[5]。磁路提供的驱动磁场直接影响GMA输出特性，因此，驱动磁场性能与磁路结构参数密切相关[6]。非均匀磁场会严重破坏GMM棒的材料特性，因此，均匀磁场强度在GMA中起着重要作用[7]。目前科研人员对GMA磁路的设计已经进行大量研究，并取得丰硕的研究成果，但更多关注的是偏置磁场选取、磁回路设计和磁场建模[8-10]。对磁漏减小、磁场强度大、磁场强度均匀率高的综合实验从未有过探究。本设计在给定输出位移和输出力的基础上，分别对偏置磁场选取以及GMM棒、激励线圈、磁回路的结构参数进行设计；使用Ansoft Maxwell仿真分析GMA的磁路。结果表明，GMM棒中轴线上的磁场强度均匀率得到很大程度的提高，为GMA磁路的结构设计和实际应用奠定基础。

2 GMA结构与工作原理

GMA结构，如图1所示。工作原理为：通过调节激励线圈输入电流大小来控制GMM棒的伸缩；GMA倍频现象由永磁体产生的偏置磁场消除；外壳、碟簧、上端盖和十字形输出杆构成预紧装置，使GMM棒获得更大伸缩量；水冷腔外套筒、相变材料和线圈骨架构成相变温控装置；线圈骨架、出水管、水冷腔、进水管组成冷却水循环装置；结合相变温控装置和冷却水循环装置之间的配合，将GMA内部热量带到外界环境，能有效抑制热误差输出；使用上下导磁环、导磁套、永磁体、十字形输出杆与GMM棒形成闭合磁路系统，可减少磁漏。

图1 GMA结构Fig.1 The Structure of GMA

3 GMA磁路的结构参数设计

3.1 偏置磁场选取

消除GMA倍频现象，需要在GMA磁路中施加偏置磁场，如图2所示。产生偏置磁场为两种：第一种是由偏置线圈中通入直流电流来产生，但发热量较大；另一种就是采用永磁体产生偏置磁场，永磁体可以在不产生过多热量的情况下产生更均匀磁场强度。因此本设计使用永磁体提供偏置磁场。

图2 倍频现象原理图Fig.2 Principle Chart of Frequency Doubling Phenomenon

GMM棒在不同预压应力下的λ-H曲线，λ为GMM棒磁致伸缩系数，H为磁场强度，如图3所示。由图3可知，当预压力为10MPa时，GMM棒的线性度最好，线性区域为（40～120）kA/m，因此偏置磁场强度为40kA/m。

图3 GMM棒在不同预压应力下的λ-H曲线Fig.3 The λ-H Curves of GMM Bar under Different Prestressing Stresses

3.2 GMM棒参数设计与选型

GMA主要性能指标参数，如表1所示。在给定GMA输出位移和输出力的条件下，去依次确定GMM棒设计与选型、激励线圈的设计、磁回路的设计。GMM棒的长度lg为：

式中：λs—饱和磁致伸缩系数。

由表1可知，GMA最大输出位移为xmax=100μm，当GMA工作在线性区域时，取GMM棒的饱和磁致伸缩系数为λs=1×10-3，则GMM棒的长度为lg=100mm。

表1 GMA主要性能指标参数Tab.1 Main Performance Index Parameters of GMA

最大输出力Fmax=1000N，GMM棒半径rg应满足：

式中：E—GMM棒的弹性模量；σ0—预压应力。

已知σ0=10MPa，GMM棒的弹性模量取最小值E=25GPa，代入式（2）计算得到GMM棒半径rg=4.6mm，考虑捻度的可制造性rg取5mm。

3.3 激励线圈参数的设计

激励线圈提供的磁场强度直接影响GMA的输出位移。因此，激励线圈的设计变得至关重要。由图4可知，携带电流激励线圈的某一段dl为：

图4 线圈内轴线任意一点P的磁场强度Fig.4 The Magnetic Field Strength of Any Point P on the Inner Axis of the Coil

式中：N—激励线圈总匝数；i—电流强度；lc—激励线圈长度。

任意一点P的磁场强度为：

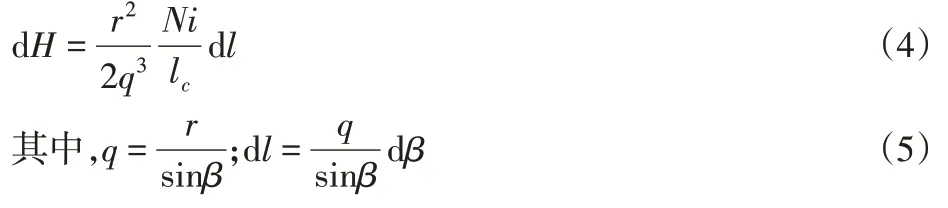
将式（5）代入式（4）得：

通过积分得P点处的总磁场强度H：

式中：cosβ1、cosβ2—任意一点P与激励线圈两端夹角。

将式（7）规范化，上下同除以lc得：

为提高激励线圈的效率，激励线圈的功率损耗P1可以表示为［11］。

式中：ρw—激励线圈的电阻率；c—绕组界面的形状影响因素；R1—激励线圈的内半径；G—激励线圈的形状系数；G随α，β变化曲线，如图5所示。G的表达式如下［12］：

图5 G随α、β值变化曲线Fig.5 Curve of G with α、β Value

由图5中已知，G值随α，β值变化曲线先增加，在α=2.5、β=3.5附近达到饱和后减小。

本设计由于有温控装置，选取电流密度为5A/mm2，当线圈截面为圆时，漆包线裸导线直径为：

式中：d0—裸导线的直径；Imax—通入激励线圈最大电流；j—电流密度。

根据国内铜线规格选择漆包圆紫铜线直径d为1.71mm。

要保证GMM棒所受磁场均匀率在95%以上，应当有：

考虑捻度的可制造性lc取110mm。

由式（12）可知，激励线圈的内半径为：

考虑捻度的可制造性R1取16mm。

激励线圈的外半径为：

线圈单位长度上匝数n1以及单位厚度上的层数n2。

式中：kη—线圈的排绕系数；kβ—线圈的叠绕系数。根据漆包线的直径，这里kη取1.05；kβ取1.15。

激励线圈的总匝数：

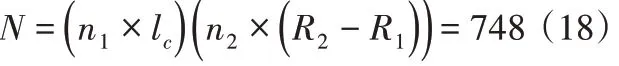
3.4 磁回路参数的设计

为使驱动磁场更加均匀，对GMA的闭合磁回路进行设计。GMM棒中的磁场强度由安培环路定律与磁通连续性定律可得：

式中：Hg、H1、H2、H3—GMM棒、上下导磁环、导磁套的平均磁场强度；l1、l2、l3—上下导磁环、导磁套的有效长度。

根据磁通连续性原理：

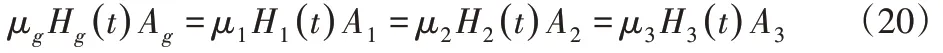
式中：μg、μ1、μ2、μ3—GMM棒、上下导磁环、导磁套的相对磁导率；Ag、A1、A2、A3—GMM棒、上下导磁环、导磁套的等效截面积。

由式（19）和式（20）联立得：

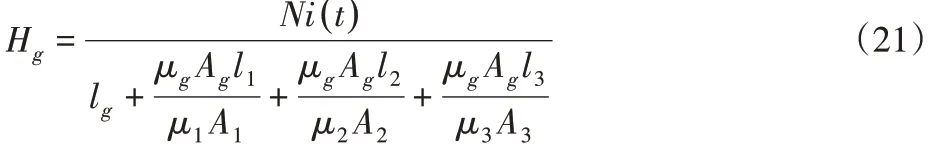
当上下导磁环尺寸相同，将其磁通底面圆形等效成矩形，式（21）可以简化为：

式中：r—上下导磁环的半径；h—上下导磁环的厚度；b—导磁套的厚度。

由式（22）可知，在GMM选定的情况下，μg、Ag、lg定值；在N、i一定时，影响GMM棒中轴线上的磁场强度Hg为上下导磁环磁导率μ2、导磁套磁导率μ3、上下导磁环半径r、上下导磁环厚度h、导磁套厚度b；当上下导磁环磁导率μ2、导磁套磁导率μ3的相对磁导率越大，GMM棒中轴线上的磁场强度Hg越大，因此GMA磁回路中的上下导磁环、导磁套材料选用高导磁率的工业纯铁［13］。GMM棒中轴线上的磁场强度与上下导磁环的半径、厚度以及导磁套厚度的曲线图，如图6所示。由图6（a）～图6（c）可知，GMM棒中轴线上的磁场强度随导磁环厚度、半径、导磁套厚度的增大呈现先增大后减小的变化趋势，且导磁环厚度为10mm、导磁环半径为63mm、导磁套厚度为12mm时GMM棒中轴线上的磁场强度最大。

图6 导磁环厚度、导磁环半径、导磁套厚度对GMM棒中轴线磁场强度影响Fig.6 Influence of Thickness of Magnetic Guide Ring，Radius of Magnetic Guide Ring and Thickness of Magnetic Guide Sleeve on Magnetic Field Strength of Central Axis of GMM Rod

4 GMA磁场有限元仿真分析

4.1 GMA磁场有限元模型的建立与参数设置

由GMA结构的二维图模型可知，GMA的磁路为轴对称结构，因此可以将其简化为二维平面模型进行静态磁场仿真分析。以GMM棒中轴线处的磁场强度均匀率作为衡量GMA磁回路优劣标准，磁场强度均匀率为：

GMA磁路中各材料相对导磁率，如表2所示。由第三部分GMA磁路的结构参数设计可知，仿真条件为：偏置磁场强度为40kA/m；GMM棒为φ（10×100）mm；激励线圈长度、直径、内半径、外半径分别为110mm、1.71mm、16mm、40mm；导磁环厚度、半径为10mm、63mm；导磁套厚度为12mm。GMA磁回路在Ansoft Maxwell 15.0环境下建立有限元仿真模型并设置材料属性；设定线圈激励源，激励源大小为NI值；永磁体材料是铷铁硼，由于永磁体用来产生偏置磁场，故还要设置其矫顽力；对其进行自由网格划分；激励条件是当激励电流为10A；边界条件为balloon边界条件。在建立模型后，将该模型应用于当前的激励条件和边界条件下，最终求解磁场后处理的有限元解。

表2 各材料相对导磁率Tab.2 The Relevant Permeability of Various Materials

4.2 仿真结果分析永磁体对GMM棒中轴线磁场强度影响

GMM棒中轴线上的磁场强度随永磁体厚度增大呈现先增大后减少的变化趋势，且当永磁体厚度为11 mm时磁场强度最大，如图7（a）所示；GMM棒中轴线上的磁场强度均匀率随永磁体厚度增大几乎不发生变化趋势，如图7（b）所示。随永磁体半径的增大，GMM棒中轴线的磁场强度均匀率呈现先增大后减少的变化趋势，且永磁体半径为12 mm时磁场强度均匀率最高，如图7（c）所示；GMM棒中轴线上的磁场强度随永磁体半径增大几乎不发生变化趋势，如图7（d）所示。

图7 永磁体对GMM棒中轴线磁场影响Fig.7 The Influence of Permanent Magnetic on the Central Axis Magnetic Field of GMM Rod

4.3 理论计算与仿真结果比较

将超磁致伸缩驱动器的激励线圈结构参数：N=748，I=10A，lc=110mm，d=0.8mm代入式（7）可得：

将GMM棒等距离分11段：X=｛ 0；10； 20；30； 40；50； 60；70； 80；90；100｝的磁场强度代入式（24），GMA磁场分布云图，如图8所示。理论计算结果与仿真结果表明：GMM棒中轴线处最小和最大磁场强度为96.53kA/m和98.88kA/m，磁场强度均匀率为97.62%；理论计算结果与仿真结果，如图9所示。

图8 磁场分布云图Fig.8 The Magnetic Field Distribution

图9 计算结果与仿真结果对比Fig.9 The Comparison of Calculation Results with Simulation Results

5 结论

通过对GMA磁路结构设计和分析，得到GMA磁路中偏置磁场选取以及GMM棒、激励线圈、磁回路的结构参数。（1）激励线圈的轴向长度是GMM棒长度的1.1倍时，作用在GMM棒上的磁场强度最均匀。（2）永磁体厚度主要用来提高GMM棒中轴线上磁场强度，且GMM棒中轴线上的磁场强度随永磁体厚度的增大呈现先增大后减小的变化趋势；永磁体半径主要用来提高GMM棒中轴线上磁场强度均匀率，且GMM棒中轴线上的磁场强度均匀率随永磁体半径的增大呈现先增大后减小的变化趋势。（3）通过Ansoft Maxwell仿真分析得到GMM棒中轴线处磁场分布较均匀，仿真结果表明GMM棒中轴线处最小和最大磁场强度为96.62kA/m和98.88kA/m，均匀率为97.62%；磁力线按设计的磁回路分布并且没有明显的漏磁现象。