混合动力汽车能量管理的自适应交叉NSGA-II优化

张珠让，周 南

（1.咸阳师范学院，陕西 咸阳 712025；2.湖南大学，湖南 长沙 410082；3.长沙商贸旅游职业技术学院，湖南 长沙 410116）

1 引言

混合动力汽车为缓解能源危机和环境污染问题提供了契机，因此混合动力汽车产业得到了蓬勃发展。混合动力汽车的能量管理策略和动力总成参数决定了车辆的动力性能和耗能［1］，因此研究混合动力汽车能量管理策略与参数优化对节能减排、提高市场竞争力具有重要意义。

混合动力汽车的能量管理策略可分为4类：使用逻辑门限值的能量管理策略、发动机最佳工作点的瞬时优化策略、全局最优控制策略、神经网络等智能控制策略。逻辑门限值的控制策略由于计算量小、控制策略简单，因此实用性较强，文献［2］使用多参数门限值与瞬时优化相结合进行能量自适应控制，提高了燃油经济性；瞬时优化策略的核心思想是通过合理分配转矩，使瞬时等效燃油消耗最小，文献［3］使用瞬时优化方法对船舶混合动力系统进行了优化，有效减少了系统油耗。瞬时优化结果在全局下未必最优，全局优化方法是全局意义下的最优解，包括动态规划、变分法等，文献［4］设计了两层控制器，使用全局优化实现顶层控制优化，使用瞬时最优实现底层控制优化，此方法提升了系统整体效率。智能控制基于智能控制理论，对混合动力系统进行推理决策，文献［5］使用粒子群算法优化能量管理规则参数，提出了能量管理规则智能优化方法，节省了车辆燃油。以上能量管理方法各有利弊，寻找一种规则简单、计算量小且能够有效提高车辆性能的能量管理方法是当前研究热点。

这里研究了混合动力汽车的控制参数优化问题，建立了混合动力系统仿真模型，以降低油耗和减少有害气体排放为目标建立了优化模型，提出了自适应交叉NSGA-II算法的参数多目标优化方法，达到了降低油耗和减少有害气体排放的目的。

2 混合动力汽车构型及模型

2.1 混合动力汽车构型及工作模式

这里研究的混合动力汽车构型，如图1所示。此混合动力系统具有两个离合器，离合器1控制发动机与电机连接与断开；离合器2控制发动机或电机与传动轴间的连接与断开。

图1 混合动力系统Fig.1 Hybrid Energy System

通过控制离合器1与离合器2的通断和电机工作情况，动力系统可以实现启动模式、纯电模式、电机助力驱动模式、发动机驱动且充电模式、发动机驱动模式、制动充电模式、机械制动模式、滑行模式、停车充电模式和驻车模式等10种工作模式。

（1）启动模式：在启动模式下若电机电量充足，则使用电机供电驱动车辆；若电机电量较低，则电机转动拖拽发动机至怠速，而后喷油点火，拖拽过程结束。

（2）纯电模式：由于车辆低速下排放性能差，则当车速较低且电机能够满足转矩要求时，使用纯电机驱动车辆。

（3）电机助力驱动模式：当车辆爬坡或急加速时转矩需求较大，此时使用电机助力发动机，使发动机工作在高效点。

（4）发动机驱动且充电模式：当整车转矩需求不大且电池电量较低时使用此模式，保证发动机工作在高效区。

（5）发动机驱动模式：当车辆转矩需求大于电机最大转矩，且小于发动机最优转矩时，使用此模式。

（6）制动充电模式：当电池SOC值未达到上限，且车辆需要制动时，使用制动充电模式，达到能量回收的目的。

（7）机械制动模式：当电池SOC值已达到上限且车辆需要制动时，使用机械制动模式。

（8）滑行模式：当车辆无需动力且无需减速时，进入滑行模式。

（9）停车充电模式：车辆在启动状态下无转矩需求且电池SOC低于下限值时进入停车充电模式，当电池SOC到达上限值时退出此模式。

（10）驻车模式：当车速低于阈值且需求转矩为0，系统判断驾驶员停车意图，此时进入驻车模式。

2.2 混合动力汽车仿真模型

混合动力系统包括发动机、电机、电池、离合器、变速箱、主减速器、制动器、车轮、驾驶员等部件，在此给出发动机模型、电机模型、电池模型、驾驶员模型的建立方法。

（1）发动机模型。发动机模型基于试验数据通过插值法得到。发动机输出转矩Te为转速Ne的多项式函数，为：

式中：Te—发动机输出转矩；Ne—发动机转速。

发动机燃油消耗量为［6］：

式中：Q—燃油消耗量；ρ—燃油密度；Pe—发动机功率；ge—燃油消耗率。

（2）电机模型。在混合动力系统中，电机既可以作为电动机使用，也可以作为发电机使用。当作为电动机时，其输出功率Pm-out为：

式中：Pm-out—电动机输出功率；Tm—电机转矩；Nm—电机转速；ηm—电机工作效率。

当电机作为发电机使用时，电机功率Pm-in为：

式中：Pm-in—电机的输入功率。

（3）电池模型。将电池模型等效为一个电压源和一个电阻，则电池端电压和输出功率为：

式中：Ub—电池端电压；Eb—电动势；Ib—充放电电流；Rint—电池内阻；Pb—电池输出功率。

（4）驾驶员模型。驾驶员模型根据车辆需求转矩和电机可供最大转矩，得到电机在此工作状态下的效率，并解算出电机电流，过程为：

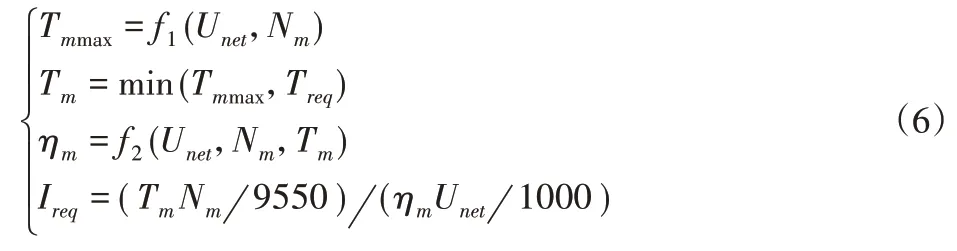
式中：Tmmax—电机外特性转矩（即电机最大转矩）；f1()—电机外特性曲线；Unet—动力总线电压；Treq—需求转矩；f2()—电机工作效率拟合曲线；Ireq—电机需求电流。

（5）车辆需求功率。车辆需求功率包括克服空气阻力、滑动阻力、爬坡阻力和加速需求等方面的功［7］，为：

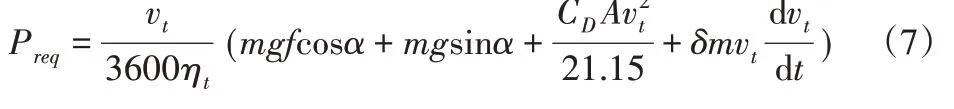
式中：Preq—车辆需求功率；vt—车速；ηt—动力系统传动效率；m—汽车质量；f—滚动摩擦系数；α—车辆坡度；CD—空气阻力系数，A-迎风面积；δ—汽车质量换算系数。

3 能量管理策略

3.1 基于逻辑门限值的混合动力分配

能量管理策略是根据需求转矩和车辆当前状态，按照某一目标对电机和发动机的动力配比进行优化。逻辑门限值计算量小且易于实现，因而得到了广泛应用。混合动力汽车的主要驱动模式包括纯电驱动、发动机驱动和混合驱动，按照发动机工作效率最高原则，三种驱动模式的区间划分，如图2所示。

图2 各驱动模式区间划分Fig.2 Interval Division

逻辑门控制方法根据发动机特性、电机特性、车辆状态、电池SOC值、整车需求转矩确定车辆工作模式的切换条件。此混合动力汽车使用电池为磷酸铁锂电池，电池内阻在SOC的（0.3～0.8）区间范围内较小，因此SOC工作上限初步设置为0.8，下限初步设置为0.3。发动机最大转矩记为Temax，电池SOC工作上限值记为Shi，SOC工作下限记为Slo，电池当前SOC值记为S，充电阈值记为Schg，电机最佳转矩记为Topt，纯电驱动最大车速记为vmmax，制动回收最小车速记为vmin，电机工作转矩系数记为Km，电机充电转矩系数记为Kchg。则各工作模式执行条件及转矩分配为：

（1）停止模式。执行条件：ɑt＜ɑ0且vt＜v0。转矩分配为：Te=Tm=0。式中ɑ0为加速度阈值，v0为速度阈值，当加速度和速度均小于阈值时，车辆停止。

（2）纯电模式。执行条件：0＜Treq＜Km·Tmmax且S＞Slo且v＜vmmax。转矩分配为：Te=0，Tm=Treq。

（3）发动机驱动充电模式。执行条件：Treq＞0且S＞Slo且S＜Schg。转矩分配为：Te=Treq+Tchg，Tm=Tchg。

（4）发动机驱动模式。执行条件：Km·Tmmax＜Treq＜Topt或v＞vmmax。转矩分配为：Te=Treq，Tm=0。

（5）混合驱动模式。执行条件：Treq＞Topt且S＞Slo。转矩分配为：Te=Topt，Tm=Treq-Topt。

（6）制动充电模式。执行条件：Treq＜0且v＞vmin且S＜Shi。转矩分配为：Te=0，Tm=Treq。

3.2 工作模式切换逻辑

在3.1节中给出了6种重要工作模式的切换条件，在此给出车辆10种工作模式的切换逻辑流程图，如图3所示。

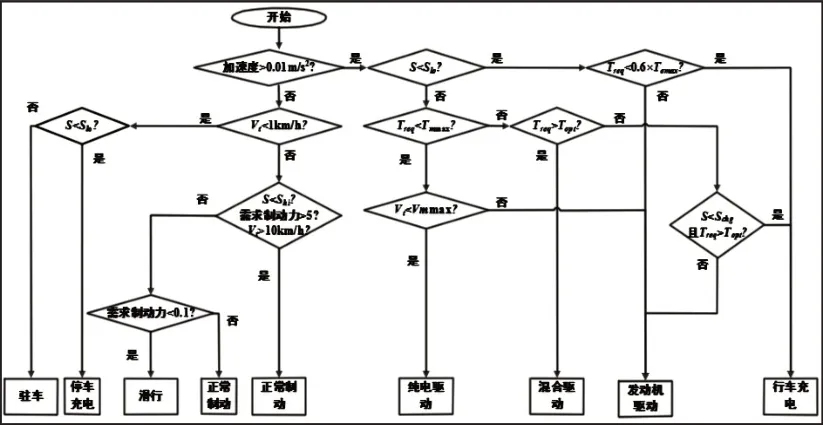
图3 切换逻辑图Fig.3 Switching Logistic Diagram

图3中参数设置为：加速度阈值ɑ0=0.01m s2，速度阈值v0=1km h，制动回收最小车速vmin=10km h。

4 控制参数优化

4.1 优化模型建立

这里以车辆的等效百公里油耗和有害气体排放量为优化目标，即：

式中：X—优化变量；F(X)—多目标优化函数；Fuel(X)—等效百公里油耗；CO(X)—一氧化成排放量；HC(X)—碳化氢排放量；NOx(X)—氮氧化合物排放量。

选择对车辆排放性能和经济性有显著影响的5个控制策略参数为优化变量，变量及其取值范围，如表1所示。

表1 优化参数及取值范围Tab.1 Optimizing Parameters and Changing Range

表1中SOC工作上限值Shi和下限值Slo是参考磷酸铁锂电池高效工作区确定的；为了保证电池具有充分电量，SOC充电阈值Schg应略大于SOC工作下限值；电机工作转矩系数Km与充电转矩系数Kchg的取值范围根据电机效率MAP图在高效区域选择。

优化问题的约束条件包括最高车速约束、百公里加速时间约束、最大爬坡度等3个方面，即：

式中：vmax—最高车速；t0-100—（0～100）km/h的加速时间；imax—最大爬坡度。

4.2 NSGA-II算法

NSGA-II算法在遗传算法选择操作上进行了改进，加入了非支配排序和精英保留策略，使算法能够得到多个优化目标的Pareto前沿解。

（1）非支配排序［8］。记优化目标数量为T，若对于任意一个优化目标i都有fi(XA)≤fi(XB)，则称个体B被个体A支配。若在个体A不被种群中任意个体支配，则称A为非支配个体。对所有个体进行非支配排序时，所有非支配个体为第1非支配层；除第1非支配层的其余个体，再次进行非支配排序，得到第2非支配层；重复以上过程，直至所有个体排序结束。经过以上排序可知，个体非支配层越小，说明个体越优。

（2）拥挤度算子。在介绍精英保留策略前，必须对拥挤度算子进行说明。拥挤度用于描述同一非支配层的基因间距，基因间距越大（即拥挤度越大）说明基因多样性越好。每一非支配层两端的基因间距值设定为∞，其余基因间距为：

式中：dk—基因间距（即基因拥挤度）；f ik+1、f ik—在优化目标i上个体k相邻个体的目标函数值。

（3）精英保留策略。种群规模记为N，基因经过遗传操作后，父代与子代混合为2N的种群，将此混合种群进行非支配排序，从最小层非支配层开始保留，当种群规模恰好多于N时，从最大层非支配层中去除拥挤度最小的前若干个体，使种群规模恰好为N［9］。

4.3 融入自适应交叉算子的NSGA-II算法

传统NSGA-II算法中使用SBX算子进行交叉操作，父代记为p1、p2，SBX算子生成的子代记为c1、c2，则：

式中：βSBX—SBX算子生成的随机变量，即：

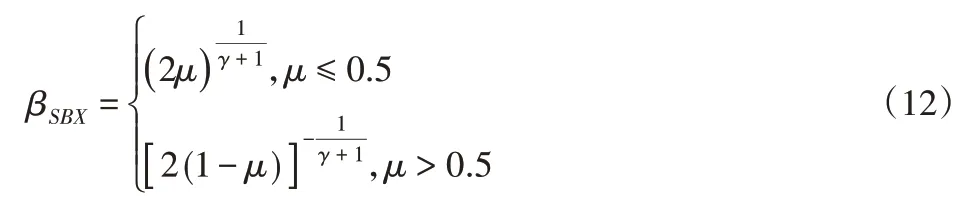
式中：μ—（0，1）间均匀分布的随机数；γ—作者自行定义的非负数。由于参数γ的设定具有较大的随机性和主观性，文献［10］提出了基于正态分布的NDX算子，为：

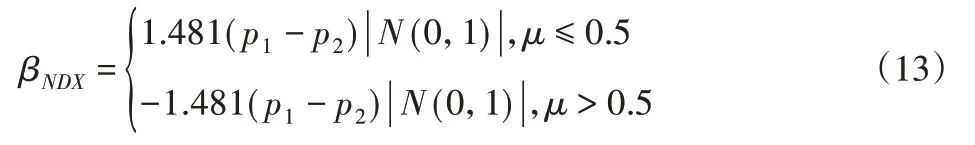
式中：|N(0，1)|-符合标准正态分布的随机变量。

NDX算子比SBX算子具有更强的搜索能力和更广泛的搜索能力，但是βNDX值无法随着迭代次数自适应改变。在算法初期是算法的探索阶段，此时基因多样性好，分布广泛，应使用较大的β值促进基因执行交叉操作而产生新基因；在算法后期，算法更加注重局部的细致搜索，应减小β值而保护较优基因。基于以上考虑，这里提出了基于t分布的tDX算子。t分布曲线与正态分布相似，曲线形态与自由度n直接相关。自由度n越小则t分布曲线峰值越小，两端越高；自由度n越大则t分布与正态分布越相似。基于这一特性，设计随迭代次数自适应变化的自由度n为：

式中：t—算法当前迭代次数；tmax—算法最大迭代次数。

分析式（14）可知，当迭代次数t迭代至0.618tmax时自由度n达到120，t分布与正态分布重合。基于t分布的交叉算子β值为：

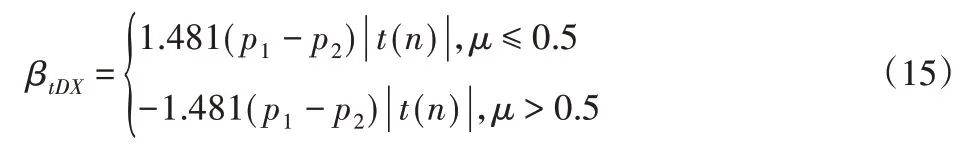
分析式（13）、式（14）和式（15）可知，算法初期自由度n较小，t分布较为分散，β值大概率取较大值，促进基因执行交叉操作；算法后期自由度n较打，t分布较为集中，β值大概率取较小值，交叉作用减弱，能够防止优良基因被破坏。通过以上分析，tDX算子实现了随迭代次数自适应变化。NSGA-II算法流程已经成熟［11］，这里不再给出。

5 实验验证

5.1 算法性能测试

首先对自适应交叉NSGA-II算法的性能进行测试，从ZDT标准测试函数中选择ZDT1测试函数测试算法的收敛性，ZDT1测试函数的Pareto前沿特征为凸，函数为：

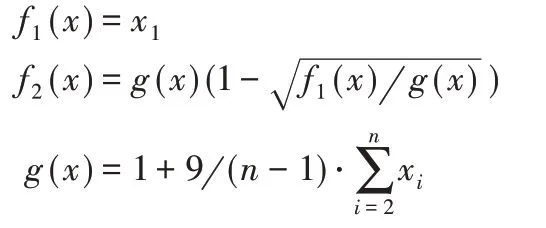
其中，n=30，xi∈[0，1]，f2(x)即为ZDT1测试函数。算法收敛性定义为算法搜索最优解集与参考解集的最小距离，即：

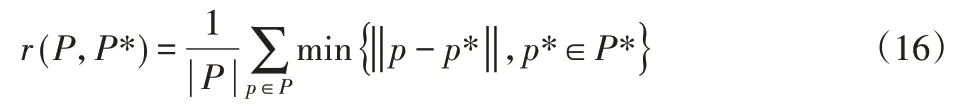
式中：r(P，P*)—算法收敛性指标；P—算法求得的解集；P*—参考解集；p—集合P中的元素；p*—集合P*中的元素。

分析式（16）可知，r(P，P*)越小，表示算法搜索的最优解集与参考解集越接近，即算法的收敛性越好。使用ZDT1函数分别对传统NSGA-II算法、文献［10］改进NSGA-II算法与这里改进NSGA-II算法进行测试，收敛性，如图4所示。

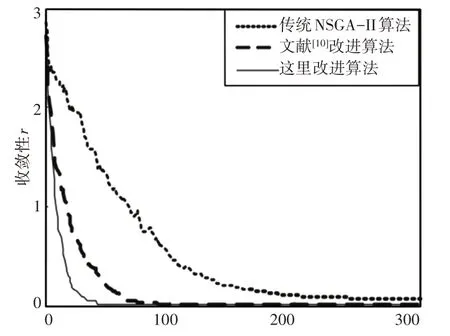
图4 收敛迭代过程Fig.4 Convergence Iteration Process

由图4可以看出，传统NSGA-II算法的收敛速度最慢，文献［10］改进NSGA-II算法的收敛速度次之，这里改进NSGA-II算法收敛速度最快。从收敛结果看，这里改进NSGA-II算法与参考解集距离最近，也即这里改进NSGA-II算法搜索的前沿解最佳。这是因为这里提出的基于t分布的交叉算子能够随算法迭代次数自适应变化，满足算法前期和后期不同的搜索需求。

5.2 优化结果及分析

使用自适应交叉NSGA-II算法进行混合动力汽车参数优化，算法参数设置为：种群数量为20，交叉概率为0.9。在NEDC循环工况中进行400次优化，共得到351组可行解，其中91组为Pareto前沿解，如图5所示。

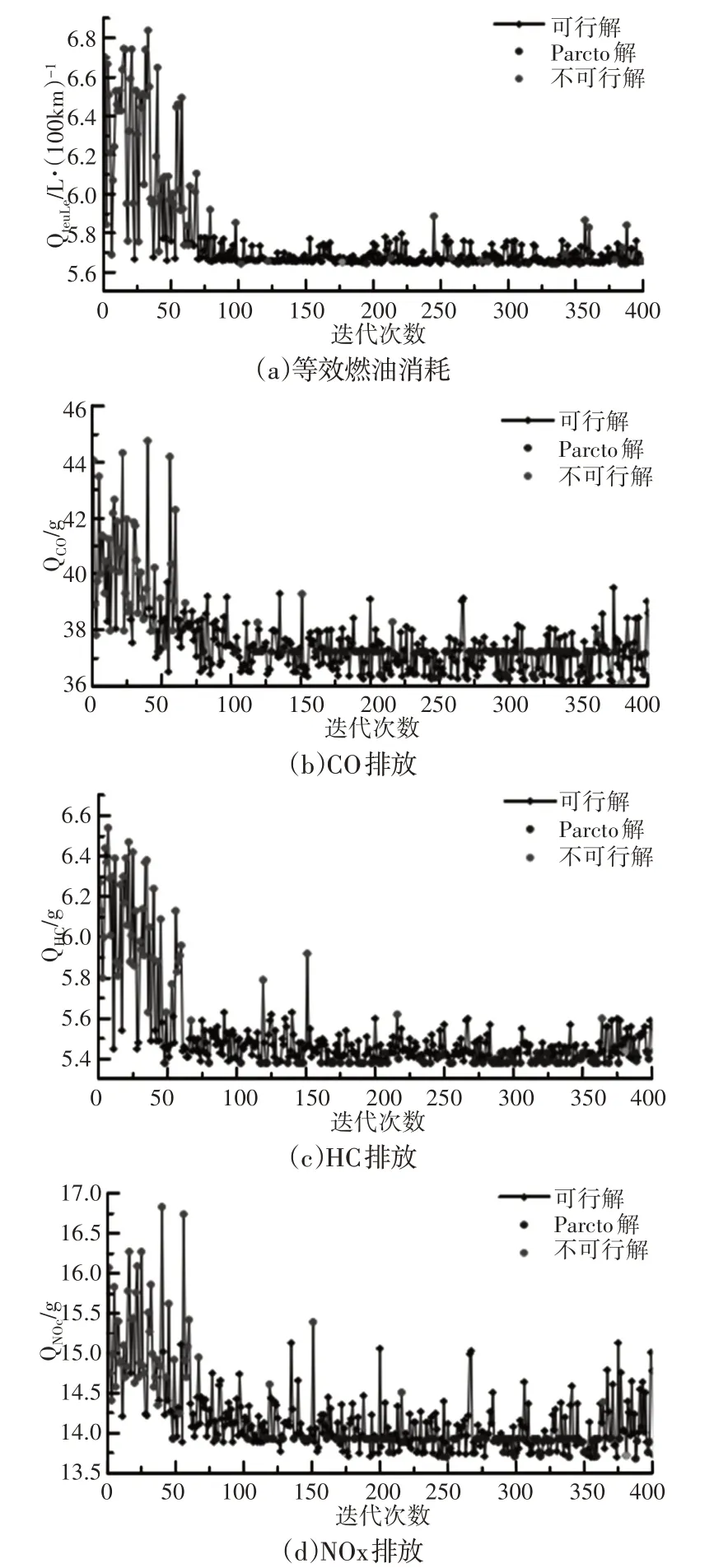
图5 自适应交叉NSGA-II算法搜索结果Fig.5 Searching Result of Adaptive Crossover NSGA-II

由于篇幅有限，优化得到的91组pareto前沿解难以全部给出，从Pareto前沿解中选择1组参数与现有参数进行对比结果，如表2所示。车辆现用参数为：Shi=80，Slo=30，Schg=40，Km=0.78，Kchg=0.4。选择1组Pareto前沿解为：Shi=80，Slo=29，Schg=35，Km=0.725，Kchg=0.397。2组参数对应的优化指标，如表2所示。

表2 优化结果对比Tab.2 Comparison of Optimizing Result

由表2可知，经过优化油耗减少了8.13%，等效油耗减少了6.53%，CO排放量减少了10.97%，HC排放量减少了7.64%，NOx排放量减少了10.03%，说明自适应交叉NSGA-II算法搜索的Pareto前沿解能够减少车辆油耗和有害气体排放，实现优化目标。

使用混合动力系统仿真模型和优化后参数，仿真模型对测试工况的车速跟踪效果，如图6所示。转矩分配结果，如图7所示。

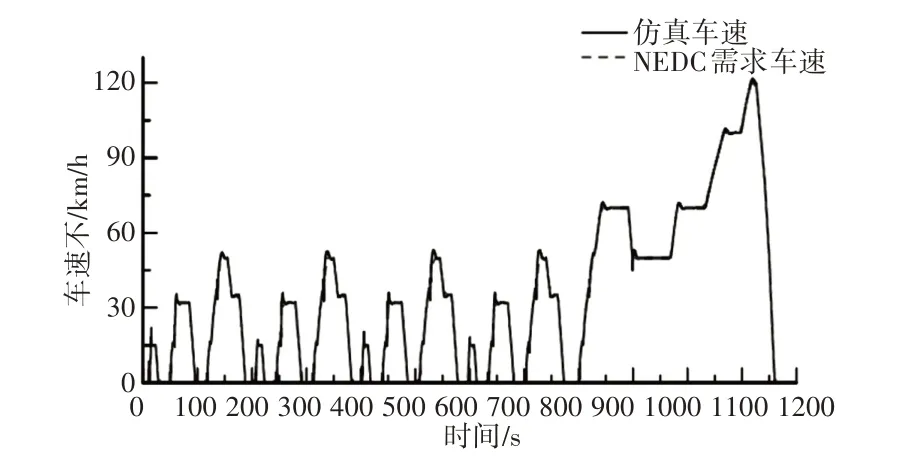
图6 车速跟踪效果Fig.6 Speed Tracking Effect

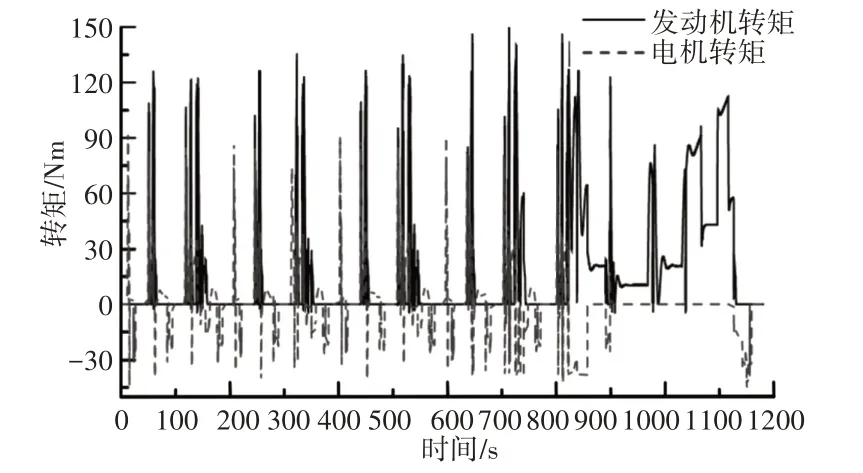
图7 转矩分配结果Fig.7 Torque Distribution Result

从图6中可以看出，仿真车速与测试工况车速几乎重合，即仿真模型能够高精度跟踪测试工况车速。对图6和图7进行联合分析可知，在车速较低的情况下主要是电机承担驱动，在车速较高的情况下主要是发动机承担驱动，与前文中逻辑门限值的设置原则一致。综合以上分析结果，基于自适应交叉NSGA-II算法的参数优化方法能够有效降低混合车辆油耗和有害气体排放。

6 结论

这里研究了混合动力汽车控制策略参数优化问题，建立了混合动力汽车的仿真模型。以降低油耗和减少有害气体排放为目标，建立了参数优化模型。制定了基于逻辑门限值的能量管理策略，提出了自适应交叉NSGA-II算法的参数多目标优化方法。经过验证，基于自适应交叉NSGA-II的参数优化方法能够有效降低油耗和减少有害气体排放。