圆柱齿轮多齿高重合度啮合齿轮参数优化研究

2022-02-23余松林刘海初潘江如

机械设计与制造 2022年2期

余松林，刘海初，潘江如，黄勇

（新疆工程学院工程训练中心，新疆乌鲁木齐 830011）

1 引言

机械采棉已经推广到在我国大部分棉花生产基地，多工位传动链是采棉机摘锭多工位专用制造装备的重要组成部分。图1所示中间小齿轮与两侧大齿轮多齿耦合是多工位传动链设计的关键。文献［1］在研究中发现由于多齿轮啮合的影响，系统会在非固有频率区出现振动的峰值，在传动设计中需要考虑多齿轮啮合对系统性能的影响。多齿啮合对系统的影响主要受齿轮相位关系的影响，行星齿轮传动就是典型的多齿啮合。文献［2］早在1967年都提出行星齿轮的相位与传动噪声有关。文献［3］提出了啮合相位关系由位置角和齿轮齿数确定。文献［4］提出了重合度直接反应齿轮工作中同时啮合齿数的多少，是齿轮副连续平稳工作的重要条件。文献［5］提出来高重合度外啮合齿轮齿根弯曲应力计算方法进行了深入研究。文献［6］提出了基于遗传算法的高重合度圆柱齿轮传动多目标优化设计思想。文献［7］提出了瞬时重合度的概念。

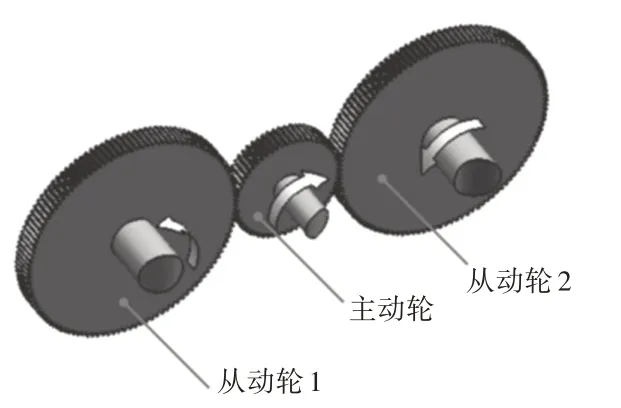
图1 多齿轮啮合示意图Fig.1 More Gear Mesh Diagram

这里在诸多学者研究的基础之上，通过对齿轮啮合区域瞬时重合度的分析，推导出主动轮旋转一个周期，瞬时重合度的变化频率ω与Z、N1、N2之间的数学关系（Z为主动轮齿数，当重合度ε为小数时，ε介于两个正整数N1和N2之间），得出主动轮圆周均布n个从动轮的基本条件是ω/n为正整数，并求得从动轮之间相位角相差2π/n是满足n对齿啮合力相等的基本条件。建立高重合度齿轮多目标优化数学模型，以理想点法为多目标优化理论，采用MATLAB遗传算法直接搜索工具求解齿轮参数最优解，通过Adams仿真验证在相同边界条件下参数优化后的齿轮啮合力幅值更小，啮合力变化更平稳。

2 基于瞬时重合度的多齿啮合力分析

齿轮啮合的重合度不仅影响齿轮传动的效率［8］，而且影响齿轮的平稳性、可靠性和使用寿命，因此重合度是影响齿轮传动性能的关键要素之一。

2.1 啮合区域瞬时重合度分析

重合度是指齿轮啮合线与基圆齿距的比值，反映的是工作齿轮啮合轮齿对数的平均值。但是在实际传动过程中，不可能为小数，齿轮啮合的齿数会出现规律性变化，如图2所示的齿轮啮合重合度为1.688，实际啮合线两侧0.668Pb（Pb为基圆齿距）为双齿啮合区域，中间的0.332Pb为单齿轮啮合区域，因此齿轮的实际重合度（瞬时重合度）是非连续和交替变化的［9］。

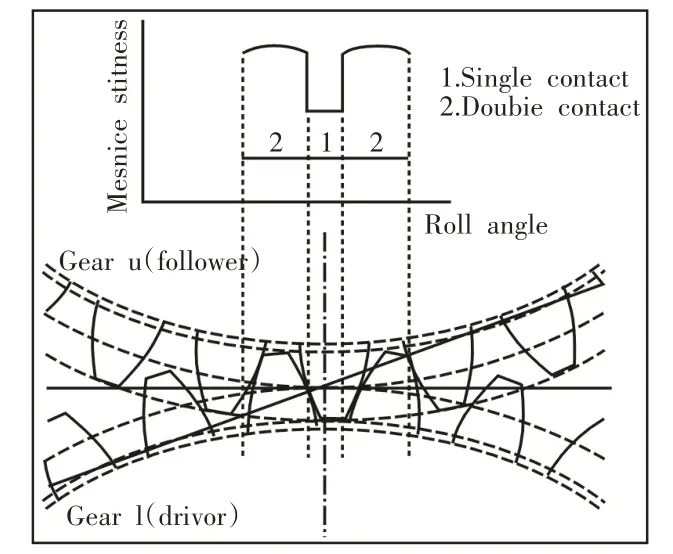
图2 因重合度变化啮合刚度变化示意图Fig.2 Because of Coincidence Degree Meshing Stiffness Changes

齿轮啮合区域示意图，如图3所示。令齿轮的重合度ε介于两个正整数N1与N2之间（N2=N1+1），Pb为基圆齿距，B1B2为齿轮啮合线。在实际传动过程中瞬时重合度只可能为N1或N2。结合齿轮啮合区域示意图经分析可知B1C1和C2B2区间瞬时重合度为N2，C1C2区间瞬时重合度为N1。

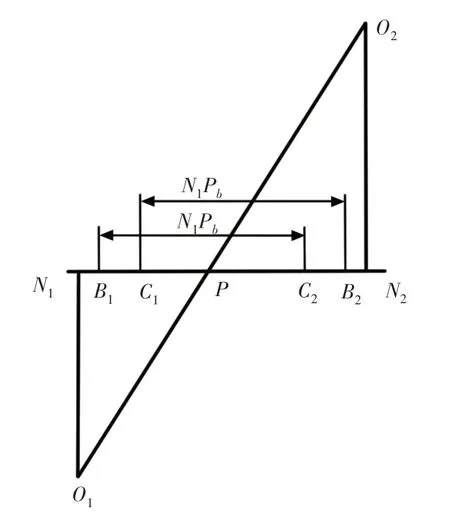
图3 圆柱齿轮啮合区域示意图Fig.3 Cylindrical Gear Meshing Area Map

由重合度的定义可知：

式中：B1B2—齿轮啮合线长；Pb—基圆齿距；ε—重合度。

由（1）可知：

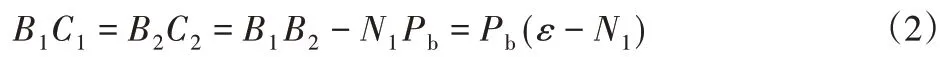
式中：B1C1和C2B2—重合度为N2啮合区域；ε—介于两个正整数N1和N2的重合度（N1＜ε＜N2）则：

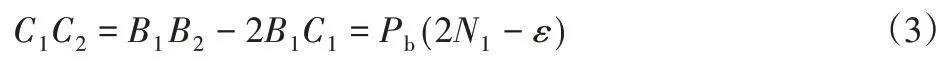
式中：C1C2—重合度为N1的啮合区域

式中：m—模数；ɑ—压力角。

由式（1）～式（4）可知B1C1，C1C2与齿轮压力角ɑ和模数m间的数学关系。

2.2 多齿啮合力分析

多齿啮合时，如果瞬时重合度不等，则会出现齿轮传动偏载，传动失去平衡，增大传动噪声，使系统的振动峰值出现在非固有频率区［11］。1个主动轮同时与2个相同从动轮均载啮合传动平稳后，瞬时重合度不等时啮合力变化情况，在同一时刻两对齿啮合瞬时重合度不等则接触应力不等。因此多齿啮合瞬时重合度相等及其重要，尤其是多齿均载荷的工况，会减少轮齿传动过程中的冲击，延长齿轮的寿命。

图4 瞬时重合度不等啮合力变化规律示意图（ε=1.79）Fig.4 The instantaneous Contact Ratio of Different Contact Force Change Rule

齿轮在啮合过程中瞬时重合度是非连续性规律变化，当一对齿轮进入啮合状态时，N2对齿进入B1C1啮合区域，随着时间的推移，将会有1对齿脱离啮合，出现N1对齿啮合进入C1C2啮合区域。当进入C2B2啮合区域时，又将会有N2对齿工作，如此往复循环。瞬时重合度变化规律，如图5所示。

图5 瞬时重合度变化规律示意图Fig.5 The Instantaneous Contact Ratio Change Rule

由图5可知，瞬时重合度变化一个周期，啮合线的长度为N1Pb。由于主动轮旋转一周啮合线总长度为Z*Pb，则轮齿瞬时重合度的变化频率为：

式中：ω—轮齿瞬时重合度的变化频率；Z—主动轮齿数。

为了保证多对齿轮啮合的重合度时刻相等，则多个从动轮必须以相同的步调与主动轮啮合。如主动轮圆周均布n个从动轮，必须满足ω/n为正整数，则从动轮之间相位角相差2π/n。满足以上条件的两对齿啮合平稳后的啮合力变化规律示意图，如图6所示。

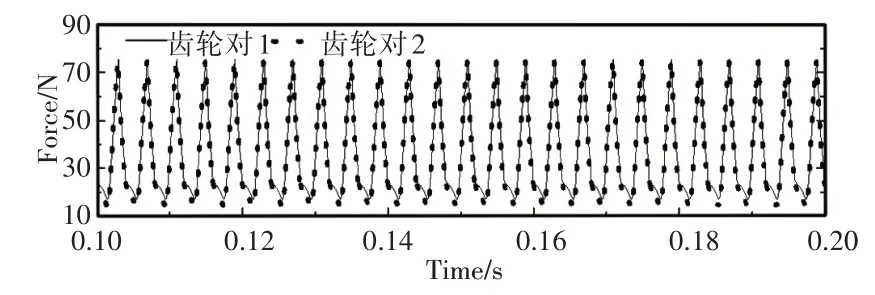
图6 瞬时重合度相同啮合力变化规律示意图（ε=1.8441）Fig.6 The Instantaneous Contact Ratio is the Same Contact Force Change Rule

由上图可知，在同一时刻啮合力大小基本相等，但由于重合度不高（ε=1.8441），传动中会有单齿啮合，导致啮合力会出现线性变化，在单齿啮合和双齿啮合交替时会有一定的冲击，因此提高重合度是保证传动平稳的有效途径。

3 齿轮多目标优化数学建模

齿轮重合度是决定齿轮传动连续性和平稳性重要因素。由1.1和1.2的分析可知，齿轮的模数m和压力角ɑ对瞬时重合度和重合度都有直接的影响。在多对齿轮啮合的齿轮参数设计中，不只是要满足常规齿轮设计的胶合度，传动比，接触强度以及弯曲强度等限制还要对齿轮齿数以及重合度等加以控制，采用多目标优化设计是满足这种设计要求最快速有效的办法之一。

3.1 目标函数确定

3.1.1 高重合度

令第一目标函数为：

式中：ɑɑ1—齿轮1的齿顶圆的压力角；

ɑɑ2—齿轮2的齿顶圆的压力角；

ɑ′—啮合角；

Z1，Z2—主动轮和从动轮齿数；

ε—重合度。

其中，

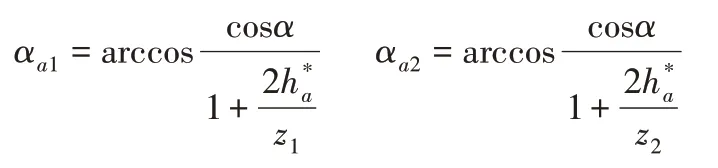
3.1.2 等弯曲强度

齿轮安全系数是齿轮可靠性的重要指标，在齿轮设计中确保啮合齿轮寿命接近，缩小啮合齿轮安全系数差，这里令啮合齿轮安全系数差最小为第二目标函数。

式中：SF1，SF2，，σFE1，σFE2，b1，b2，m，Z1，Z2，K1，K2，T1，T2，YFɑ1，YFɑ1，YSɑ1，YSɑ2—啮合齿轮主从动轮弯曲强度安全系数，弯曲疲劳极限，齿宽，模数，齿数，载荷系数，扭矩，齿形系数，应力修正系数。

3.2 施加约束条件

（1）接触强度约束

式中：SH1，SH2，SHmin，σHlim，b1，b2，d1，d2，ZE，K1，K2，T1，T2，u—啮合齿轮主从动轮接触强度安全系数，最小接触安全系数，接触疲劳强度极限，齿宽，分度圆直径，弹性系数，载荷系数，转矩，齿数比。

（2）弯曲强度限制

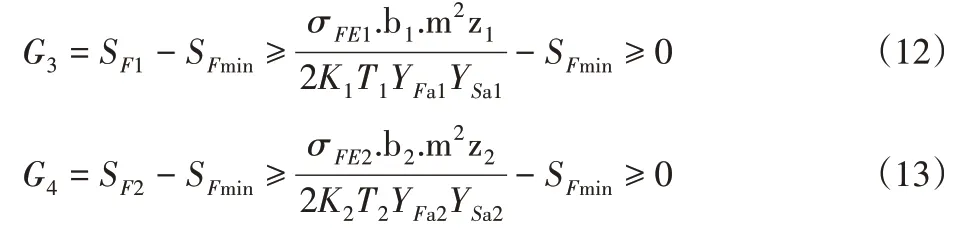
式中：SFmin—最小弯曲安全系数。

（2）重合度约束

ε≥2，若ε＞或=2，可以确保齿轮传动过程中至少两对齿啮合，提高轮齿的承载能力和传动平稳度。

（4）胶合强度限制

由于胶合是高重合度齿轮传动的主要失效形式之一，当重合度1≤ε≤3.5就要考虑胶合强度，尤其是高重合度（ε≥2），因此有必要对胶合强度加以约束。

式中：SB—齿轮胶合强度安全系数；

SBmin—最小胶合强度安全系数。

（5）传动比限制

式中：Z1，Z2—传动齿轮的齿数，且为正整数。

（6）齿数约束

（7）压力角约束

压力角是齿轮的重要参数之一，随着压力角的针大，齿轮的抗弯曲强度，抗胶合强度以及接触应力等都会逐渐增强，但压力角过大则影响齿轮啮合的重合度。国内常见齿轮压力角为20°，但是不少学者的针对压力角的研究范围选择是（15～25）°。

3.3 变量选择

由确定的目标函数可知，影响目标函数的变量因子有啮合齿轮的齿数Z1，Z2，齿轮模数m，齿宽b1，b2和压力角ɑ。

令优化设计变量X=（X1，X2，X3，X4，X5，X6，X7）=（Z1，Z2，m，b1，b2，ɑ）

4 齿轮参数多目标优化

4.1 优化理论

针对多目标优化问题通常都是将多目标问题转化为单目标问题，通过采用加权系数法找到最优解。但加权系数法是人为的根据实际情况对多个目标函数设置权重，具有一定主观性。理想点法可以弥补加权系数法的不足，所谓理想点法就是先求解p个单目标的最优解：

然后求评价函数Ф（z）的极小值minФ［f（x）］。

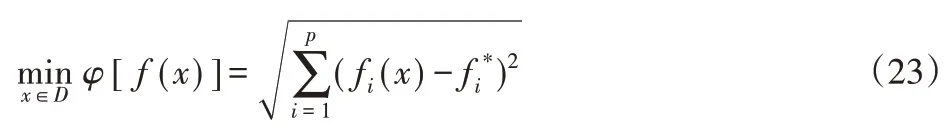
函数minФ［f（x）］的解就是所求的近似最优解。

4.2 优化求解

从齿轮优化数学模型可以知道，该数学模型包含2个目标函数和10个约束条件，约束条件中既有边界约束也有非线性约束。这种多变量多目标优化的本身特点很适合采用MATLAB遗传算法和MATLAB直接搜索工具来处理。但MATLAB遗传算法通常的计算结果是最优解集，而MATLAB直接搜索工具可以说是MATLAB遗传算法其他优化方法的补充，它可以在边界的条件，线性不等式，线性等式以及非线性约束中进一步找到最优解。因此选用MATLAB直接搜索工具优化更为合理［10］。

经计算和查阅手册可得以下参数，如表1所示。

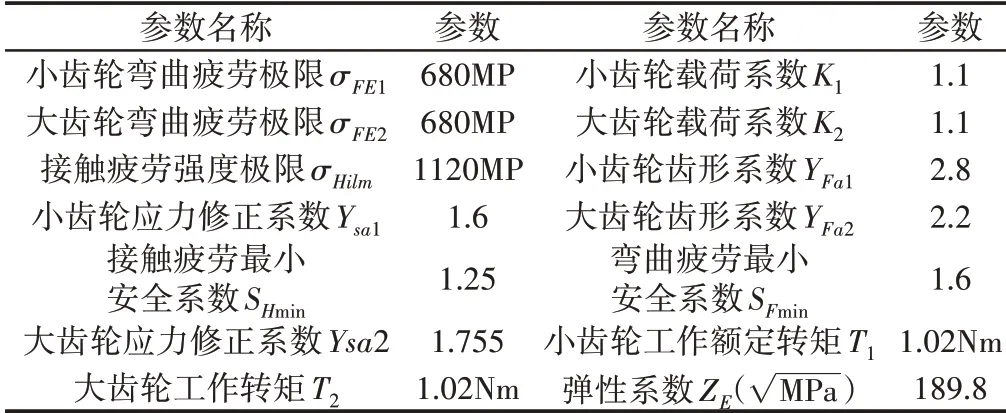
表1 计算和查阅手册参数Tab.1 Calculate and Consult Manual Parameters

根据以上参数求解minf1，minf2可得：目标函数最优解minf1=0.00322263，minf2=-2.06923且自变量X1=（17，300，1，29，25，17），X2=（50，300，2，30，30，17）。

将以上单目标函数最优解代入评价函数Ф（z）的极小值minФ［f（x）］可得：

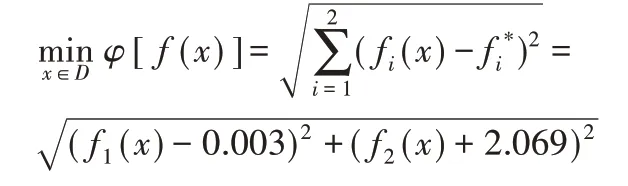
经计算可得minФ［f（x）］最优解0.00325，且对应自量值X=（50，300，1，29，25，17）。

根据以上分析可知，满足使用要求的齿轮参数最优解为：

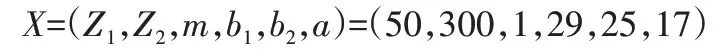
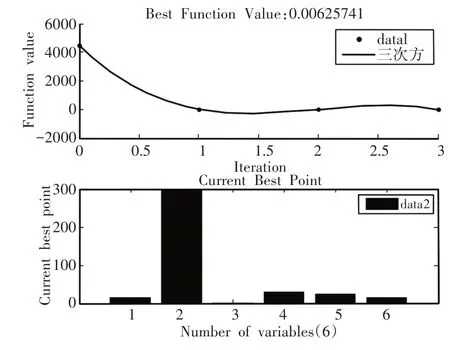
图7 minФ[f（x）]迭代最优值及最终解对应变量值Fig.7 minФ[f（x）]Iterative Optimal Value and Final Solution to the Strain Value

根据以上分析可知，满足使用要求的齿轮参数最优解为：

X=（Z1，Z2，m，b1，b2，ɑ）=（50，300，1，29，25，17）。经优化得到的参数主动轮圆周均布n个从动轮，ω/n应为正整数，从动轮之间相位角相差2π/n这一基本条件。将参数代入目标函数minf2可得重合度ε=2.0692。

4.3 仿真验证

对三组不同参数齿轮分别按照X1=（Z1，Z2，m，b1，b2，ɑ）=（43，300，2.5，25，25，20），X2=（Z1，Z2，m，b1，b2，ɑ）=（50，300，2.5，25，25，20），X3=（Z1，Z2，m，b1，b2，ɑ）=（50，300，1，29，25，17）进行三维建模导入ADAMS仿真。首先对齿轮定义转动副，并通过STEP运动函数定义中间小齿轮旋转驱动，再对两侧大齿轮施加作用力矩并创建中间小齿轮与两侧大齿轮接触，再通过建立测量函数测量仿真过程中齿轮对接触力的大小和变化，最后进行如图8所示仿真求解，为了计算的更精准定义仿真终止时间为1s，仿真步数为50000步。

图8 仿真求解Fig.8 Simulation Solution

三组齿轮仿真边界条件设置一致，经求解发现接触力都有从大到小逐且渐趋向平稳的特征，但由于三组齿轮对基本参数选择不同，传动平稳后啮合力具有变化特点，如图9所示。

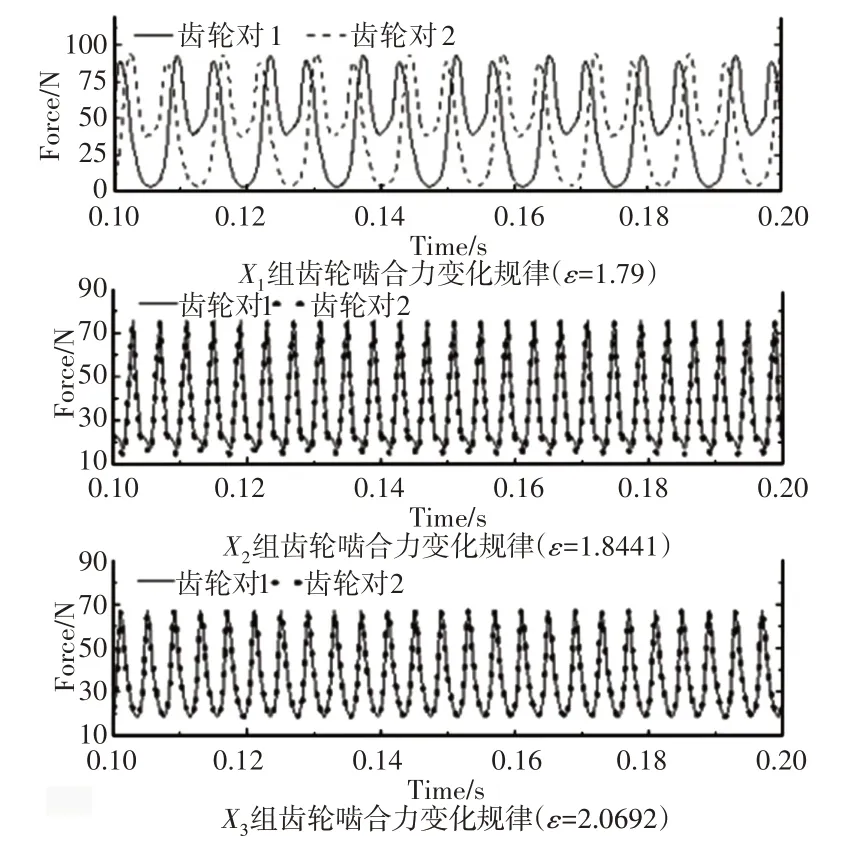
图9 齿轮啮合力变化规律对比Fig.9 Contrast of Variation Law of Gear Meshing Force

由以上可知，X1组齿轮参数不能满足两对齿轮瞬时重合度相等，所以在同一时刻两对齿啮合接触应力不等，且出现较大峰值；X2组齿轮参数能满足两对齿轮瞬时重合度相等，在同一时刻啮合力大小基本相等，但由于重合度不高（ε=1.8441），导致接触力出现线性变化；X3组齿轮参数能满足两对齿轮瞬时重合度相等且重合度较高（ε=2.0692），两对齿轮齿啮合步调一致，啮合力大小相等，接触力呈现非线性变化，传动更平稳。