基于Dspace轻型货车EPS系统控制策略研究

2022-02-23商显赫林幕义

机械设计与制造 2022年2期

商显赫，林幕义，2，童亮，2，马彬

（1.北京信息科技大学机电工程学院，北京 100192；2.北京电动车辆协同创新中心，北京 100192）

1 引言

电动助力转向（Electric Power Steering）是通过助力电机产生的助力扭矩，辅助驾驶员完成转向过程的一种汽车辅助驾驶系统［1-2］。与其他转向系统相比，EPS系统具有节能、环保、易于组装、良好的操纵稳定性、便于调整助力特性、易于维护等一系列的优点，已成为汽车横向控制的研究热点。EPS的助力控制通常使用传统的PID控制方法，确定目标电流并且跟踪目标电流，由于计算量少、易于实现和实时性好，在控制领域应用较为广泛，但PID电流控制方法也存在着一些问题：整定的参数不一定能够使系统达到最佳的工作状态，而且抗干扰性能差。为了解决PID控制的缺点，采用具有快速响应特点和参数变化及干扰不敏感且物理易于实现的滑膜变控制策略，对轻型货车的助力模式展开研究。

首先利用Matlab/Simulink建立基于汽车二自由度的EPS系统模型和控制策略模型，对滑模控制策略进行离线仿真和参数调节，然后对PID控制策略通过衰减曲线法进行参数整定，比较和分析两种控制策略的控制效果，最后，利用Dspace可以自动代码生成的优势，建立了基于Dspace循环球式电动助力转向试验台，完成轻型货车在助力模式下控制策略的验证。

2 电动助力转向系统的建模

所研究轻型货车采用的是循环球式转向器，直接用数学公式对其建模，计算量较大且存在一定复杂性，如果把绕主销的回正力矩等效到转向器的螺杆上，循环球式转向器看作一个具有惯性的阻尼原件［3］，通过这种方式，把轻型货车的方向盘、扭矩传感器、循环球式转向器、轮胎等实物硬件可以整合成一个数学模型，见公式（1）。

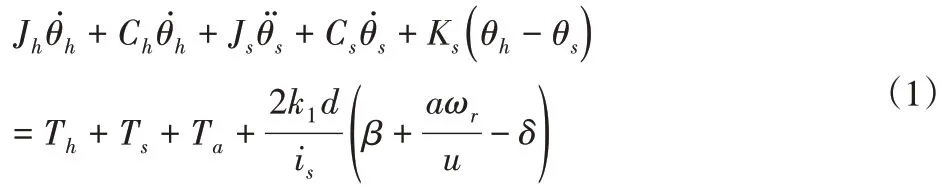
电机模型为：

转向柱转角与电机转角的关系为：

汽车二自由度模型为：

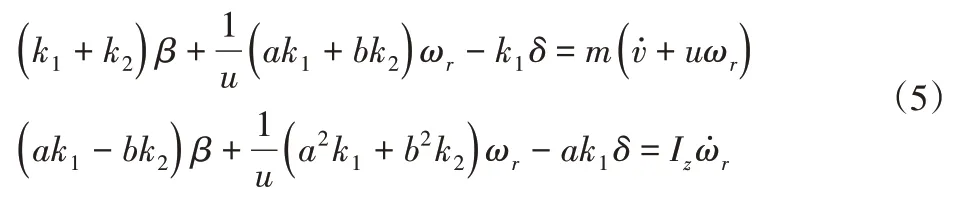
式中：Jh、Js、Jm、k1、k2—转向盘与转向柱上轴、等效到转向器螺杆、电机的转动惯量、前后轮侧偏刚度；Ch、Cs、Cm、ɑ、b、u、v—转向盘与转向柱上轴的阻尼、等效到转向器螺杆上的阻尼、电动机阻尼、从质量中心到前后轴的距离、车辆的横向速度、车辆的侧向速度；θh、θs、θm、δ、β、ωr—转向盘角度、转向柱下轴角度、电机角度、车轮角度、质心侧偏角和横摆率；Th、Ts、Tm、Tɑ—方向盘扭矩、扭矩传感器扭矩、电机扭矩、助力扭矩；Ks、Ke、Kɑ—转向柱刚度系数、反电动势常数、电磁转矩系数；is、im—转向器传动比、减速机构传动比；Iz、m—绕OZ轴的转动惯量、汽车质量。

3 电动助力特性曲线的选择

助力电机的目标电流主要与汽车的车速和转动方向盘的转矩有关，对于EPS系统助力特性曲线，采用简单易设计的直线型作为设计目标。助力特性曲线无助力区（死区）由Th0扭矩值决定，一般取Th0=1N·m，从减轻驾驶员的驾驶疲劳角度考虑，设置方向盘转矩Thmax=7N·m时，电机将提供最大的扭矩输出，根据汽车原地转向的半经验式（6）：

式中：f—轮胎与路面间的滑动摩擦系数；G1—汽车前轴负荷；p—轮胎气压；Mr—原地转向阻力矩；Tf—等效到转向轴上的阻力。

根据计算，得到助力电机最大助力电流Imax=20A，电机的助力扭矩与汽车车速有关，所研究的目标车型的最高时速为90km/h，此时，电机辅助转矩为0N·m，辅助电流为0A，并且不同速度下的辅助电流的变化被认为是线性的，设计出一种直线型的助力特性曲线［4-5］，如图1所示。

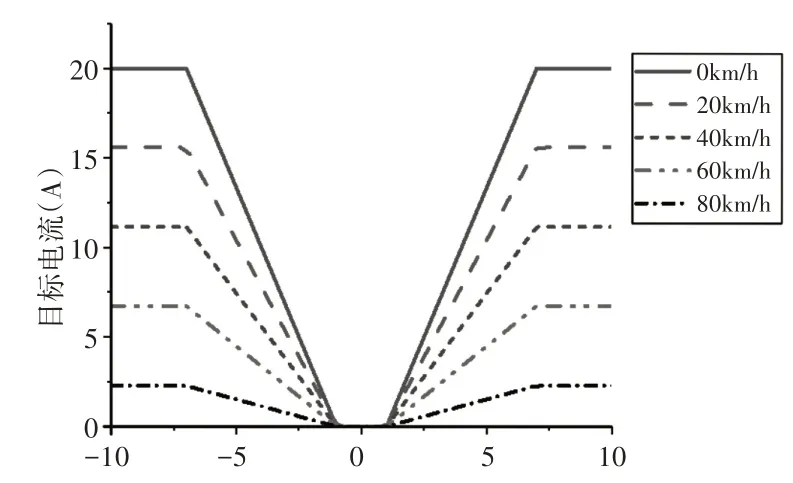
图1 电动助力特性曲线图Fig.1 Chart of Electric Power Characteristic

4 电动助力转向系统控制策略研究

4.1 助力模式下的传统PID控制策略

PID控制策略通过调节的kp、ki、kd参数值，来控制电机电流输出特性，抵消电机负载，进而实现助力控制，PID控制器的数学描述为［6-7］：

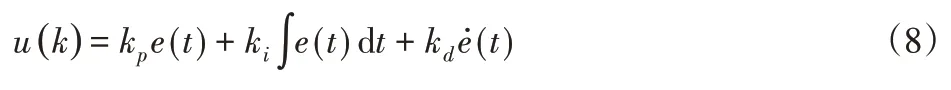
式中：u(k)—PID控制器的输出信号；

kp、ki、kd—比例、积分及微分系数；

e(t)—测量值与给定值之间的偏差；

e˙(t)—测量值与给定值偏差的导数。

4.2 助力模式下的滑模控制策略

滑模控制策略是一种变结构控制，它与PID等线性控制系统不同，它的非线性控制表现为控制的不连续性，而且控制系统“结构”的时变性，能够按照系统的即时状态（例如偏差与其导数），让“结构”动态地变动，使其满足系统基于预先设定的“滑动模式”的状态轨迹有规律地移动［8-10］，设有一个系统：

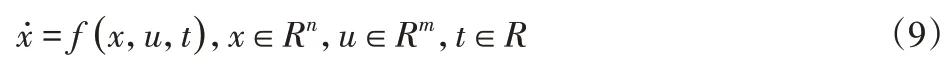
选择函数s(x)=cx，s∈Rm作为切换函数向量，根据变结构的原理，即：

这里的变结构体现在，使得：

（1）滑动模态存在，即式成立；

（2）满足到达条件后，切换迅速；

（3）保证滑动模态运动的稳定性。

滑模控制的切换函数可以改善滑动模态运动的品质，根据电动助力转向控制系统的特点，把切换函数定位为目标电流与实际电流之差，即：

几种常用的模态趋近律里，采用既可以减弱抖动又可以加快趋近时间的指数趋近律作为滑模控制的方式，其表达式为：

式中：趋近律系数ε＞0，k＞0，sgn(s)—符号函数。

对切换函数求导并带入（3）式得：

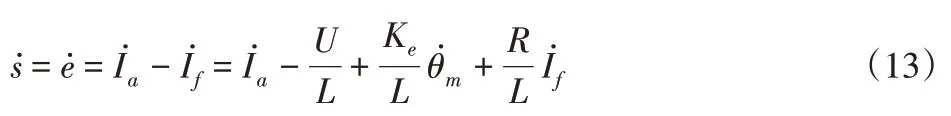
于是，推导出控制器输出量为：

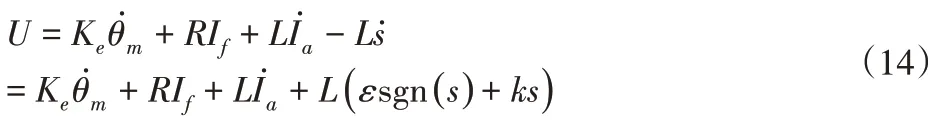
5 电动助力转向系统仿真与分析

5.1 仿真模型的建立与调试

根据推导的转向系统的数学模型、汽车二自由度模型和控制策略的数学模型，利用Matlab/Simulink软件完成电动助力转向系统各模型的建立，如图2所示。

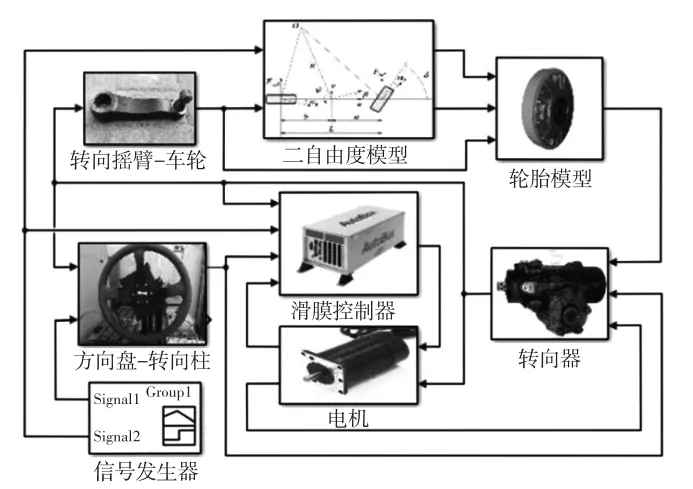
图2 EPS系统仿真模型Fig.2 EPS System Simulation Model

能够实现目标电流较好的跟随，调整PID和滑模控制策略的参数尤为关键，对于PID控制策略，调试发现控制系统很难调出等幅振荡过程，因此，采用衰减曲线法实现kp、ki、kd三个参数的调优，首先根据调试方法，调出4：1衰减振荡过程，然后根据此时的kp、衰减比例度δs和衰减周期Ts，按照衰减曲线法相应的整定公式得出调节器参数结果，如表1所示。

表1 调节器参数Tab.1 Regulator Parameters

于是根据衰减曲线法得到整定的kp、ki、kd三个参数分别为1.2、1333、0.00036。滑模控制策略参数的调整通过变动ε和k实现，过小的ε会让系统的斗振现象特别明显，而k则会影响响应时间的大小。通过在线调节的方式，设定车速为30km/h给系统5N·m阶跃输入，得到不同ε和k值对应的控制电流随时间变化的曲线，如图3所示。

图3 不同ε和k对系统的影响Fig.3 The Influence of Differentεandkon the System

根据仿真调试，从图3可以看出，当k=30、k=75时，ε越小系统的趋近速度越慢，而ε过大，有较大斗振现象出现；当ε=10时，不同的k值，对系统影响变现为k越小响应时间越小，而过大的k，系统的超调量越大，所以，经过多次调试，滑模控制策略的趋近律参数ε=10、k=75时，系统的斗振现象最小，响应时间最快，稳定性最高。

为了对比PID和滑模控制策略的控制效果，根据衰减曲线法整定的kp、ki、kd参数和调整过的ε、k参数，通过建立的仿真模型完成相同工况下的控制效果对比，设定车速30km/h，方向盘扭矩为5N·m阶跃输入，于是得到图4所示的控制效果对比结果，可以看出，PID控制策略的超调量要远大于滑模控制策略，但是滑模控制层策略的反应时间存在一定的迟滞，两种控制策略达到稳定的时间基本相同，对于系统稳定性这个角度来讲，滑模控制策略要优于PID控制策略。

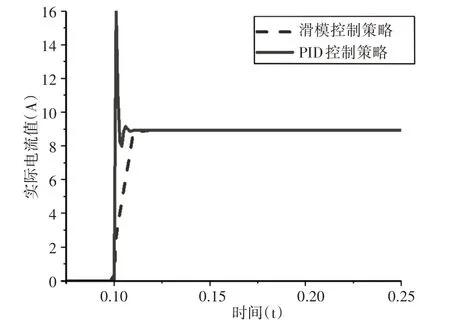
图4 两种控制策略控制效果对比Fig.4 Contrast of Control Effect of Two Control Strategies

5.2 滑模控制策略试验台架验证

为了通过电动助力转向台架试验验证所研究控制策略的有效性，将图2所示的方向盘转向柱模型用RMS方向盘代替，控制器用Dspace完成数据的处理和运算，信号输入通过RMS方向盘采集的方向盘扭矩、转角、角速度输入到Dspace中，车速信号用信号发生器进行模拟，设置每公里的脉冲数为2548个，根据频率的不同反映不同的车速，电机的反馈电流采用霍尔式电流传感器检测并经过采集卡输入到Dspace中，EPS系统的输出为滑模控制策略运算出的电压值，利用Dspace的DS1103SL_DSP_PWM模块产生PWM，之后通过电机驱动板实现对电机的驱动，汽车转向的阻力距，通过试验台架上的磁粉制动器进行模拟，由于汽车在不同车速时轮胎的附着系数发生改变，汽车阻力矩也会相应的改变，因此磁粉制动器的加载阻力通过WLKB控制器进行控制［11］。

首先进行原地转向试验，设置工况车速为0km/h，磁粉制动器的控制电流加载到3A，然后对方向盘在中间位置进行标定，顺时针转动方向盘到最右边，然后逆时针转到最左端，最后转到方向盘校准的中点。经过有助力和无助力两种工况试验，得到在助力模式下，方向盘转角和方向盘扭矩之间的关系，如图5所示。

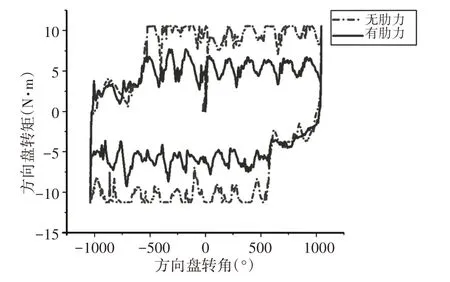
图5 方向盘转矩和转角的关系Fig.5 The Relationship Between Steering Wheel Torque and Angle

为了验证滑动模式控制策略的控制效果，通过以不同的车速旋转方向盘，将获得的电动机的实际电流值与目标电流值进行比较，得到实验结果，如图6所示。

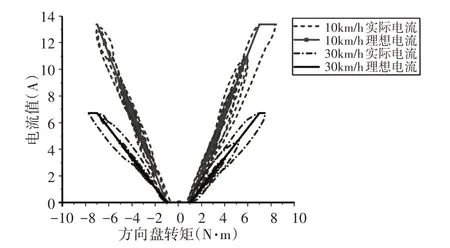
图6 不同车速电流值对比Fig.6 Comparison of Current Values at Different Vehicle Speed

从试验结果图5可以得出，有助力时，转动相同的方向盘转角会比无助力时使用的操纵力矩要小，设计的滑模控制策略可以满足转向轻便型的要求，由于RMS方向盘采集的方向盘扭矩值精度为（-10～10)N·m，所以在辅助模式下，当方向盘扭矩值超过10N·m时，曲线已经是该范围的最大扭矩值；从图6可以看出，电机实际输出的电流值会随着输入扭矩的变化和目标值保持同步，而且在不同车速时，都能够实现对目标电流的跟随，由于滑模控制策略在切换滑模面时会产生抖振的现象，因此，实际电流曲线与目标电流曲线不是完全重合，存在较小的偏差，这是滑模控制策略的缺点，但是滑模控制策略对被控对象的模型误差、对象参数的变化以及外部干扰敏感性较低，所以滑模控制策略的鲁棒性较好。