万向轴动不平衡检测的自适应变分模态分解方法

唐泽娴，林建辉，丁建明，李艳萍

（西南交通大学牵引动力国家重点实验室，四川 成都 610031）

1 引言

万向轴是高速列车CRH5的核心动力传递部件［1］，其结构细长，弯曲刚度和扭转刚度较小，因此长期运行列车上的万向轴易产生偏心。万向轴偏心引起传动轴的不平衡振动，进一步影响列车轴承、万向节等其他旋转件的工作［2］，危及高速列车的运行安全。因此，开展万向轴的动不平衡检测研究是十分重要。对此，国内外学者开展了大量的研究，其中小波变换和经验模态分解最为常用。而仅用经典小波检测万向轴的动不平衡，存在对平移敏感以及混叠效应显著等问题［3］。经验模态分解克服了基于小波分解受测不准原理的约束，具有较高的自适应性，可以提高时间和频率的分辨率，但是边界效应和混叠问题严重，存在缺乏理论支持。

近年来，由文献［4-5］提出的自适应分解方法—变分模态分解（Variational Mode Decomposition，VMD）得到广泛运用，该方法结合了希尔伯特变换、维纳滤波原理，具有完备的理论基础和优良的窄带特性。研究发现，模态个数和惩罚因子α是影响分解效果的两个重要参数。利用均一法初始化中心频率时，初始模态数直接决定初始的中心频率分布。当初始化中心频率与实际中心频率差距过大时易导致鞍点搜索时间过长，迭代次数过多，甚至出现严重的结果偏差。为了确定合适的参数，采用基于傅里叶谱峭度和能量（均方根）分布指标的模态个数确定法；依据傅里叶谱峭度增量调节惩罚因子，并将该方法运用于万向轴动不平衡的检测，通过仿真数据说明其有效性。

2 傅里叶谱峭度—变分模态分解原理及方法

2.1 变分模态分解原理

定义一个本征模态函数是一个调幅调频信号，如下表示：

式中：φk(t)—非递减函数，φ′k(t)≥0，包络非负，Ak(t)≥0，且幅值Ak(t)和瞬时频率ω k(t)：=φ′k(t)满足比相位的变换要缓慢。

作为一个自适应，近似正交的分解方法，VMD将一个复合实信号f分解成满足本征模态特征的分量信号uk。各分量uk在频域上都集中在以wk为频率中心的附近，带宽受H1高斯平滑来控制，因此，约束的变分模态分解可以表示成如下所示：

通过引入二次惩罚因子α和拉格朗日乘子λ(t)将式（2）非约束化并进一步通过乘子交替方向算法（Alternative Direction Method of Multipliers，ADMM）不断迭代更新分量和中心频率，寻找最优化的中心频率、模态分量及拉格朗日乘子。

迭代整个算法直到满足收敛条件：

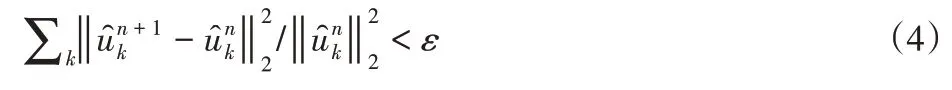
输出符合条件的所有分量。

2.2 傅里叶谱峭度

峭度是用来衡量一数据集峰度程度的指标，表示如下：

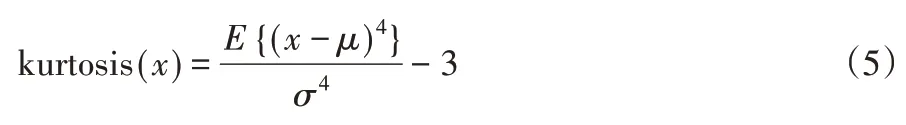
式中：x—时间序列；μ，σ—x的平均值和方差；E(·)—期望算符。

万向轴动不平衡信号由多个简谐信号和噪声复合而成，简谐信号在频谱上有突出的峰值，中心频率幅值大于频率附近的其他信号成分。定义傅里叶谱峭度为：

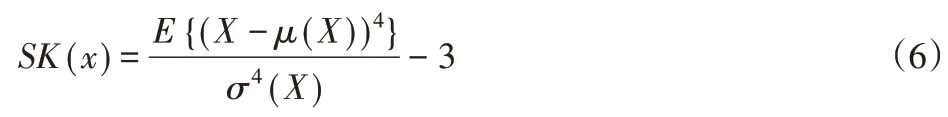
X为x对应的傅里叶变换序列。由于实测信号中噪声并非为理想的白噪声，部分噪声可能导致傅里叶谱峭度的灵敏度降低，因而引入能量指标（信号的均方根值）联合确定能量和峭度均占优的分量。定义傅里叶谱峭度-能量指标为归一化的谱峭度值和均方根乘积：

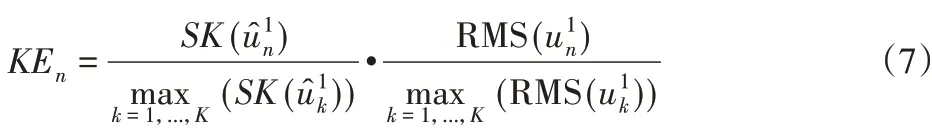
傅里叶谱峭度-能量指标能够结合谱峭度和能量二者属性，筛选出幅值较明显的非噪声信号，该指标即考虑分量在原信号中的能量占比又通过峭度指标反映其包含信息量的多少。

由于惩罚因子越大，对应维纳滤波器的通带越窄，能滤除更多噪声边频，傅里叶谱峭度随之增大，因此可根据傅里叶谱随惩罚因子的变化，选取合适的惩罚因子。

2.3 基于傅里叶谱峭度的变分模态算法实现原理

首先，通过信号傅里叶谱均方根极值点的分布进行模态个数估计并初始化中心频率。

为获取均方根值曲线和极值点分布，首先应对信号进行区域分割，分割条件满足每个区间点数m：

式中：Fs—转频；fs—采样频率；T—采样数据长度，区间长度的选取避免了在同一个区间里出现两个简谐信号成分又能保证曲线拟合时对能量分布刻画的精确性并合理控制运算复杂度。

计算每个区间内的均方根值，利用spline.m函数插值后可得到信号在频域上的RMS曲线。根据RMS曲线极值点pk将中心频率，(k=1，2，...，K)初始化为：

初始化参数后，进行VMD算法迭代。迭代依次获得和，对进行KE值计算。选取0.1为阈值，当KE＞0.1时，保留分量及中心频率，否则舍去。根据保留下的分量数，重置K。当迭代满足停止条件，输出分解结果。若分解出的模态含噪程度太高，可以通过调节惩罚因子进行降噪。将输出的中心频率作为初始化频率，从1000起不断增大惩罚因子，当傅里叶谱峭度的增量超过阈值时，输出当前惩罚因子。阈值可根据待分解信号的特征取不同值，这里设为0.01。

3 试验验证

为了验证1.6中的万向轴动平衡检测方法，搭建了万向轴动不平衡试验台。选取专修轴（轴的动不平衡量超过规定标准）作为测试轴。万向轴转速为2100r/min，取万向轴近电机端的万向节轴的垂向振动加速度信号作为信号源。对实测信号做频谱分析，得到对应的RMS分布曲线，如图3所示。将模态个数初始化为12。

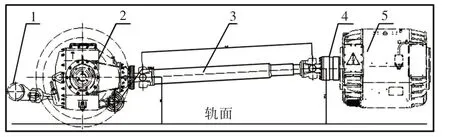
图1 万向传动轴动不平衡试验装置Fig.1 Test Installation of Cardan Shaft Dynamic Imbalance

图2 万向轴动不平衡试验数据Fig.2 Test Data of Cardan Shaft Dynamic Imbalance

图3 试验信号频谱图及RMS曲线Fig.3 Spectrum and RMS Curve of Test Signal

完成第一次迭代后，计算出的KE指标值如表所示，其中大于0.1的有分量1、5、6和10。这些分量分别对应中心频率：35Hz，178Hz，214Hz，391Hz，即转频，转频的5、6、11倍频。当α=24000时满足惩罚因子选取条件，得到分解的时频，如图4、图5所示。

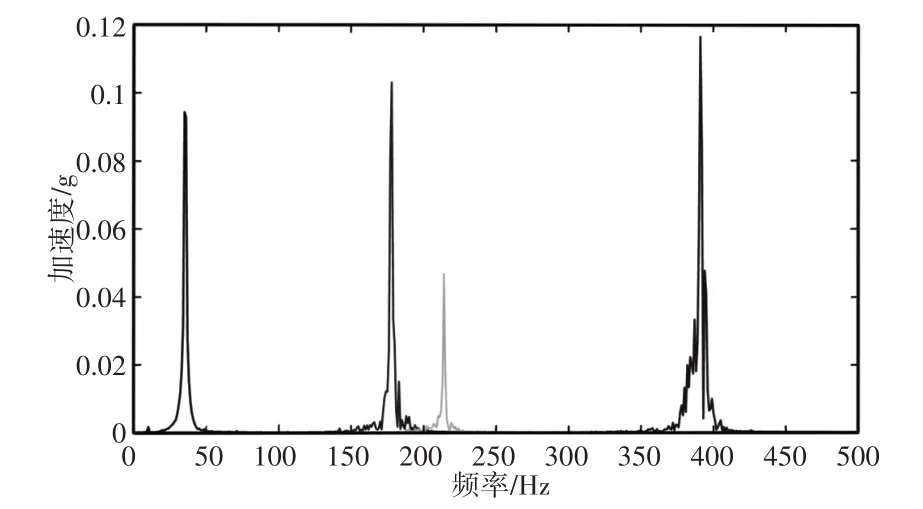
图4 试验信号分解结果Fig.4 Decomposition of Test Signal

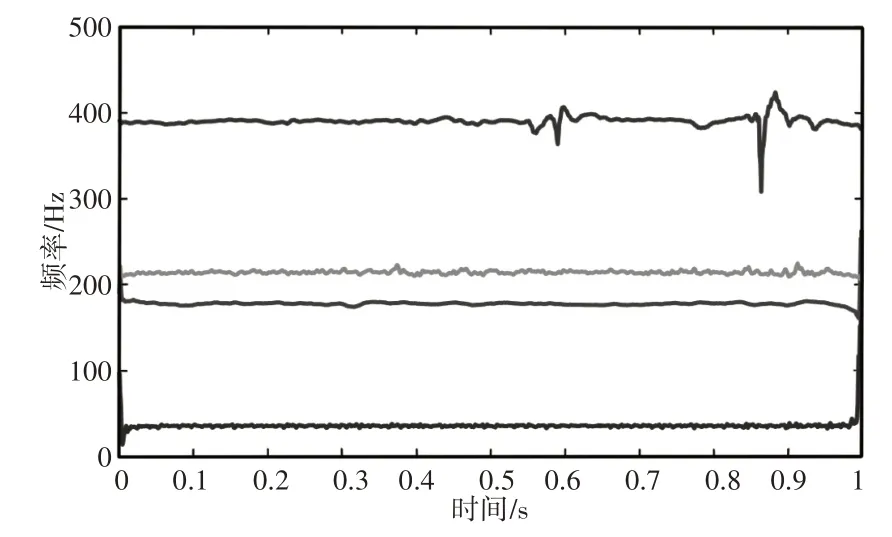
图5 分量的时频表示Fig.5 The Time-Frequency Representation of Test Signal

4 结论

变分模态分解是为了克服经验模态分解的不足而提出的一种算法，在故障特征提取上有很大的优势，但也存在不足之处，即参数难以确定。因此，根据变分模态分解类似一组自适应的维纳滤波器的特性，提出了新的模态个数及惩罚因子的选择方法，该方法利用傅立叶谱均方根和峭度值曲线具有探测谱内信息分布的特性来确定参数使VMD算法从含噪信号中较好地识别出万向轴故障频率及倍频，通过参数调节还能进一步抑制噪声。改进VMD的分解性能有所提升。但不足之处在于，在选取惩罚因子时需要多次执行VMD，增加了算法的时间复杂度。