避险车道制动床上失控车辆车轮沉陷深度研究

覃频频，吴 达，侯晓磊，万 千

（1.广西制造系统与先进制造技术重点实验室（广西大学机械工程学院），广西 南宁 530004；2.东南大学建筑学院，江苏 南京 211189；3.桂林电子科技大学建筑与交通工程学院，广西 桂林 541004；4.华蓝设计（集团）有限公司，广西 南宁 530004）

1 引言

我国避险车道的研究起步较晚，目前的避险车道设计缺乏相应的技术规范与指南［1］。随着计算机技术的发展，避险车道的研究也快速发展起来。基于离散元的PFC软件被逐步应用于避险车道失控车辆车轮与制动床集料相互作用过程数值模拟。张高强（2011）提供了一种利用颗粒流模型模拟刹车失灵货车驶入避险车道制动床后的运动过程，进而确定制动床长度的方法。结果发现颗粒流模拟是一种较为简便、实用的方法［2］。QIN（2017）搭建了砾石粒径均一的车轮－集料PFC2D模型；分析了砾石与车轮在减速过程中的相互作用；标定了砾石集料离散元的部分细观参数［3］。QIN（2019）利用车轮－集料PFC2D模型分析了砾石粒径对失控车辆停车距离的影响［4］。刘攀（2019）基于离散元理论与方法，建立轮胎与避险车道集料颗粒流模型；仿真结果表明：离散元法能够很好地模拟车辆在避险车道中的行驶过程［5］。

以上研究基于PFC2D软件建立的车轮-集料二维离散元模型由于受二维模型的限制，仅能模拟车轮的运动距离而不能模拟车轮陷入集料的沉陷深度。此外，出于简化考虑，二维离散元模型还忽略了悬架系统对减速过程的影响。车辆动力学研究表明只有充分考虑悬架系统的K&C特性，才能使轮胎的受力与车辆系统的振动接近真实情况［6-7］。

为了进一步研究悬架系统K&C特性对车轮沉陷深度的影响，基于PFC3D软件建立悬架-车轮-集料三维离散元模型，并利用标定的模型开展不同砾石粒径、驶入初速度和载重对车轮沉陷深度影响的数值模拟。研究成果不仅可以为避险车道制动床铺筑厚度设计提供理论依据，还可以为避险车道失控车辆车轮与制动床集料的相互作用过程数值模拟提供可借鉴的模型。

2 研究方法

2.1 模型的假设

离散单元法（distinct element method，简称DEM）是由美国学者Cundall P.A.在1971年基于分子动力学原理首次提出，在研究散体介质上具有很大的优势［8］，目前广泛应用于材料力学、岩土力学、弹性力学等多个领域［9-10］。PFC3D（Particle Flow Code three Dimention，简称PFC3D）是美国ItascaR公司基于离散单元法开发出来的商业离散元软件。PFC3D软件的数值模拟基于以下几点假设：（1）基本单元为球体；（2）所有实体为刚体，在接触时不会发生变形；（3）颗粒接触时，颗粒间存在微小的重叠量，但重叠量较小，相当于点接触；（4）颗粒运动遵循牛顿运动定律。

2.2 接触模型类型

PFC3D提供了线性模型、线性黏结模型、平行黏结模型等10种接触模型。工程应用中制动床的集料会因雨、雪、粉尘等原因会出现部分板结的现象，此时集料相互接触情况复杂，例如未板结的集料之间存在线性接触，而板结的集料之间存在黏结接触等现象。研究中选取豆形砾石（River Gravel）作为制动床集料，并假设集料状态维护良好，没有出现板结现象。为此，接触模型选取线性模型，模型结构，如图1所示。

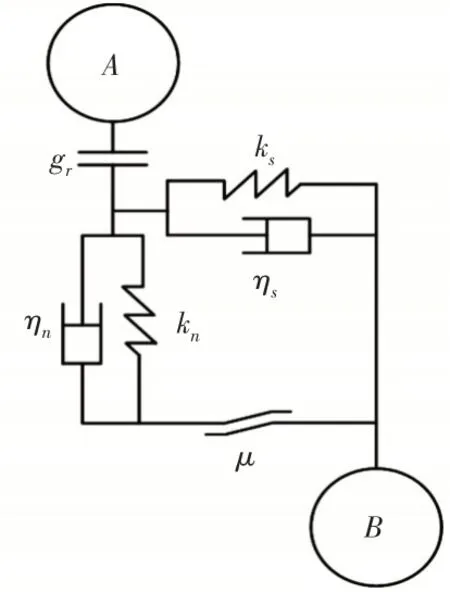
图1 线性接触模型示意图Fig.1 Schematic Diagram of Linear Contact Model

线性接触模型的gr为接触判断参数，当颗粒间的距离小于gr时，接触模型起作用。

颗粒之间的法向作用力为：

式中：kn，A、kn，B—颗粒A、B的法向刚度；ηn—颗粒间的法向阻尼；

xn—颗粒间的相对位移。

颗粒之间的切向作用力为：

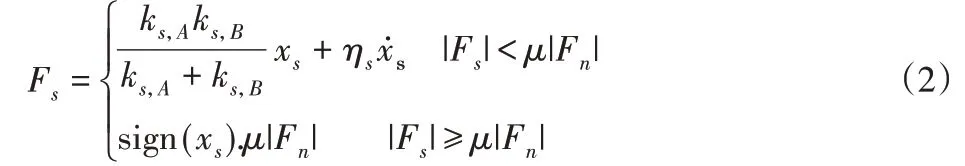
式中：ks，A、ks，B—颗粒A、B的切向刚度；ηs—颗粒间的切向阻尼；xn—颗粒间的相对位移；μ—颗粒间的摩擦系数。当|Fs|＜μ|Fn|时，颗粒间的切向力由刚度、阻尼决定；当|Fs|≥μ|Fn|时，颗粒间切向力由摩擦系数决定。

2.3 车轮离散元

车轮离散元是由多个半径相同的球体颗粒叠加而成的颗粒簇，车轮颗粒簇与真实车轮的外形相似。车轮离散元可以让车轮与砾石的接触部分离散化，成为多点接触，这样可以使轮胎颗粒与砾石间的接触力分布离散化，接触力分布更均匀，在三维空间内可以更有效地模拟带花纹的轮胎与砾石之间的相互作用情况。车轮离散元直径为1.1m，宽度为0.3m，车轮的转动惯量受传动系统影响，应根据不同车型设置。

2.4 集料离散元

砾石集料离散元用球体颗粒模拟并填满整个制动床。若建立一个全尺寸的砾石集料制动床模型（设长75m，宽1.2m，高0.6m），球体颗粒的数量将达到三百多万个，即便高性能的计算机也很难达到建模和仿真运算的要求，这也是利用三维模型研究失控车辆车轮与制动床集料相互作用较困难的主要原因。

为此，提出一个可行的解决方法，即通过分段生成与删除部分集料离散元，使得集料离散元只存在于距离车轮中心前后5m的范围之内。此时球体颗粒数量仅为全尺寸制动床模型的1/15，计算工作量大幅度减少。仿真示意图，如图2所示。

图2 仿真示意图Fig.2 Schematic Diagram of Simulation

2.5 悬架系统的建立

悬架系统的弹性元件弹簧与减振器产生的阻尼力对车轮的运动有较大影响。在PFC3D软件中建立悬架系统模型，应充分考虑悬架的垂向刚度与阻尼，车身、钢板弹簧、悬架的纵向刚度与阻尼［11］。建立的车身、悬架和车轮系统的示意图，如图3所示。

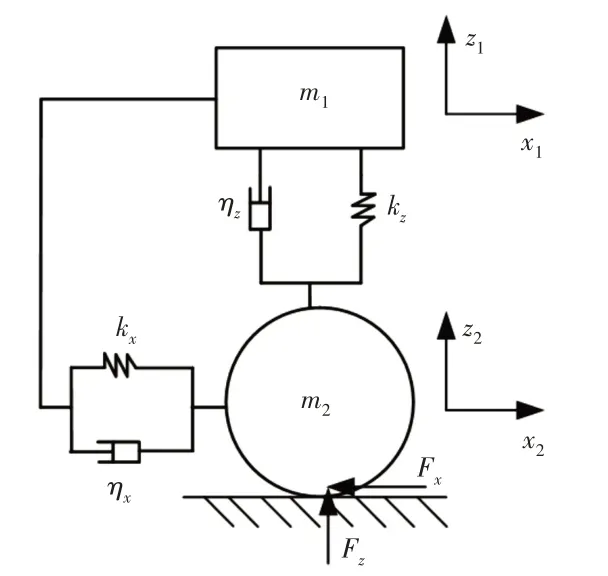
图3 车身-悬架-车轮系统示意图Fig.3 Schematic Diagram of Bodywork-Suspension-Tire system

图中：kz—悬架的垂向刚度；kx—悬架的纵向刚度；ηz—悬架的垂向阻尼；ηx—悬架的纵向阻尼；m1—车身质量；m2—车轮质量；x1—车身纵向位移；x2—车轮纵向位移；z1—车身的垂向位移；z2—车轮的垂向位移；Fx—车轮的水平作用力；Fz—车轮的垂向作用力。z方向上的坐标原点取在平衡位置，分别建立悬架系统垂直方向和纵向方向的运动微分方程，结果分别见式（3）和式（4）。

根据式（3）和式（4），利用Fish语言搭建车身与悬架系统的非实体部件，在仿真的每一个时步内求解运动学方程，分别求解非实体车身的位移、速度和实体车轮的位移、速度。根据运动方程的求解结果，计算出悬架系统对车轮的作用力。

2.6 悬架－车轮－集料三维离散元模型的建立

基于PFC3D软件搭建的悬架－车轮－集料三维离散元模型，如图4所示。模型中车身与悬架系统是通过Fish语言建模，是非实体部件，故未能在图中显示。

图4 悬架－车轮－集料三维离散元模型示意图Fig.4 Schematic Diagram of Three-Dimensional Discrete Element Model of Suspension-Tire-Aggregate

失控车辆在避险车道制动床上强制减速过程中存在以下几种能量消耗：推土阻力消耗能量、压实阻力消耗能量、动能转换等。集料与车轮的相互作用模型，如图5所示。由图5可知集料对称剖分面的截图，故不能显示车轮两侧的砾石颗粒。

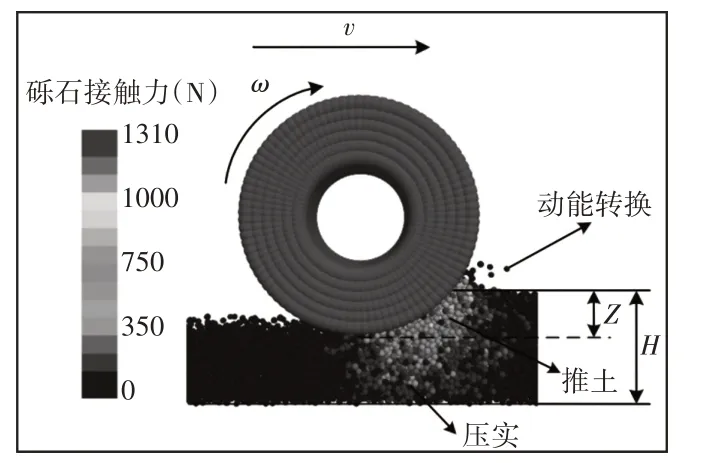
图5 集料与车轮的相互作用模型Fig.5 Interaction Model between Aggregate and Tire

3 模型的标定

标定分两个步骤：第一步，利用虚拟静力三轴压缩试验对砾石颗粒离散元参数进行；第二步，根据实车实验数据，利用仿真试验对轮胎颗粒离散元参数进行标定。静力三轴压缩试验与实车实验的数据均来自AI-Qadi（1991）的试验数据［12-13］。

3.1 集料离散元颗粒参数标定

第一阶段的虚拟静力三轴压缩试验示意图，如图6所示。需要标定的离散元颗粒参数包括：颗粒的法向刚度、颗粒的切向刚度以及颗粒的摩擦系数。

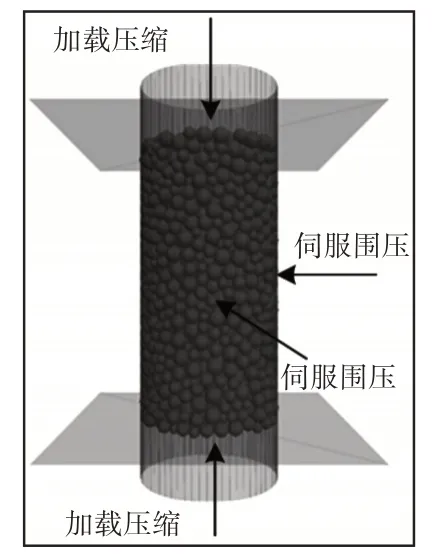
图6 虚拟静力三轴压缩试验示意图Fig.6 Schematic Diagram of Virtual Static Triaxial Compression Test

图6中的虚拟试验共生成2400个颗粒，上下两“墙”以1%的速率加载压缩试样，圆柱“墙”通过伺服机构维持围压的稳定。在3种不同的相对密实度以及3种不同围压下进行了9组试验。不断调整颗粒的参数，使得虚拟试验样品的峰值应力和峰值应变尽可能地接近实际样品。试验结果，如表1所示。颗粒微观参数，如表2所示。

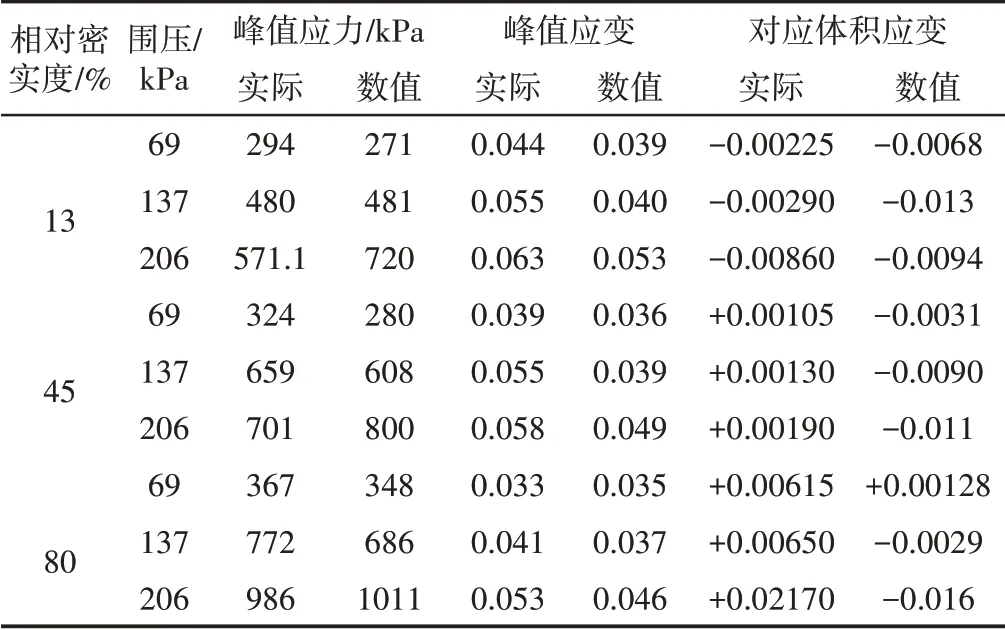
表1 虚拟静力三轴压缩试验结果Tab.1 Results of Virtual Static Triaxial Compression Test

表2 集料离散元颗粒参数Tab.2 Parameters of Aggregate Discrete Element Particles

3.2 车轮离散元颗粒参数标定

第二阶段利用实车足尺试验的停车距离、平均减速度、车轮最大沉陷深度和平均沉陷深度数据对车轮离散元颗粒参数进行标定。车轮离散元颗粒参数包括切向刚度，法向刚度和摩擦系数。仿真时调整车轮离散元颗粒参数，设置车轮初速度为v0m/s，让车轮在坡度为i的制动床上减速，记录车轮停车距离、速度和车轮沉陷量等数据结果，如图7所示。图7中1号至5号试验的车辆型号为单轴自卸车，6号至10号试验车辆型号为半挂列车。

图7中实际停车距离与模拟停车距离的相关系数为0.94，实际平均减速度与模拟平均减速度的相关系数为0.79，实际车轮最大沉陷深度与模拟最大沉陷深度的相关系数为0.79，实际平均车轮沉陷深度与模拟平均车轮沉陷深度的相关系数为0.66。从图7可以看出，实际平均车轮沉陷深度与模拟平均车轮沉陷深度相差较大，这主要是因为在实际试验中，一条车辙会被两个或者两个以上的车轮碾过，因此试验结束后测量所得的实际车轮沉陷深度要远大于模拟车轮沉陷深度。

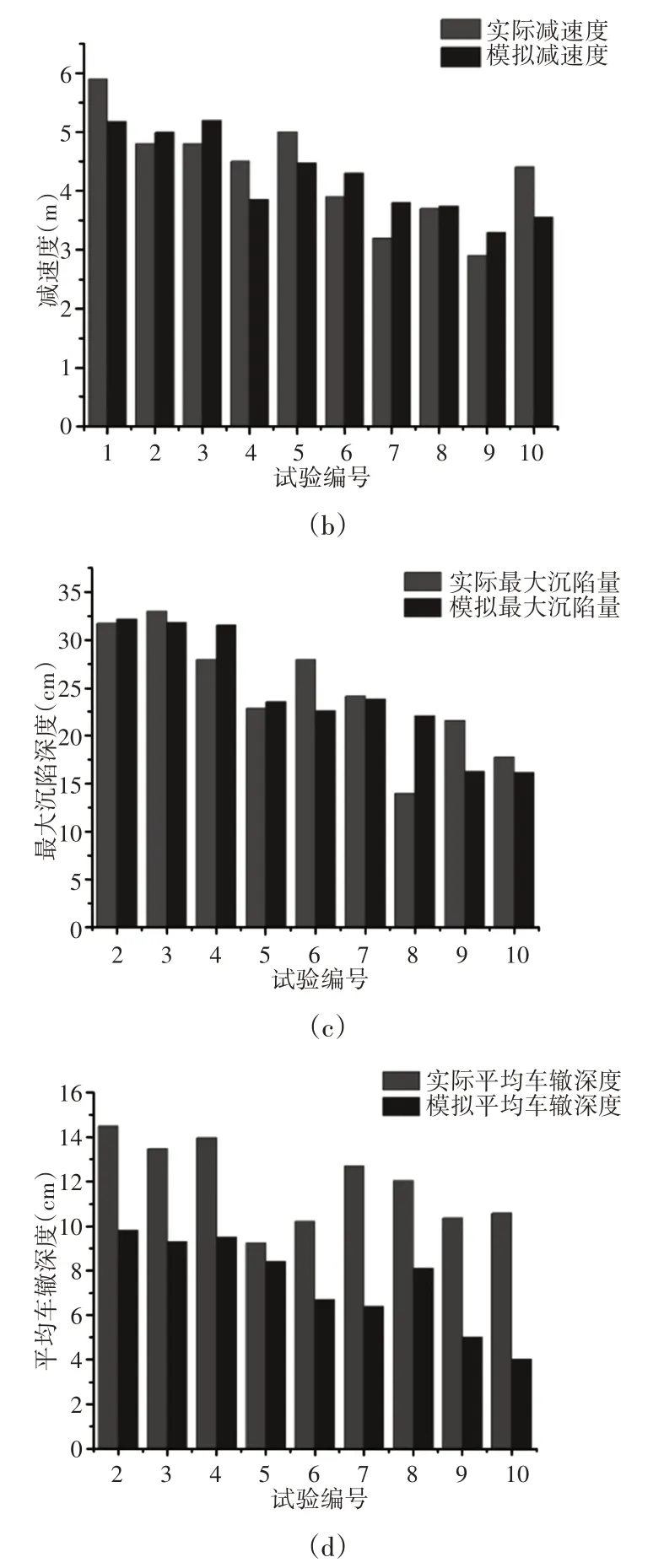
图7 车轮离散元颗粒参数标定结果Fig.7 Calibration Results of Tire Discrete Element Particle Parameters

文献［3］利用PFC2D软件建立了车轮-集料二维离散元模型并发现二维模型估算的停车距离数据优于Al-Qadi模型和FHWA方法。设置与文献［3］相同的仿真条件，将三维离散元模型的数值模拟数据与文献［3］进行对比结果，如表3所示。表中：负数—三维模拟结果的误差小于二维模拟结果的误差；正数—三维模拟结果的误差大于二维模拟结果的误差。从表3看出三维模型的各项结果都要优于二维模型。

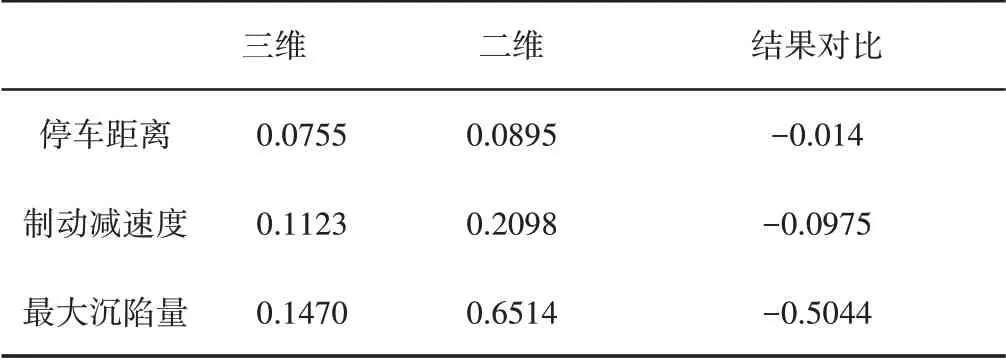
表3 仿真结果的相对误差对比Tab.3 Comparison of Relative Error of Simulation Results

在停车距离模拟中，三维模型与二维数值模型都可以达到较好的效果；但是在平均减速度与车轮最大沉陷深度的模拟中，三维模型更优于二维模型，尤其是车轮沉陷深度。以上仿真的结果反映出标定的车轮离散元颗粒参数能够使模型的数值模拟结果接近实车足尺实验数据，从而较好地实现了对失控车辆减速过程的数值模拟。标定的模型可以用于后面的数值模拟。车轮离散元颗粒参数标定结果，如表4所示。

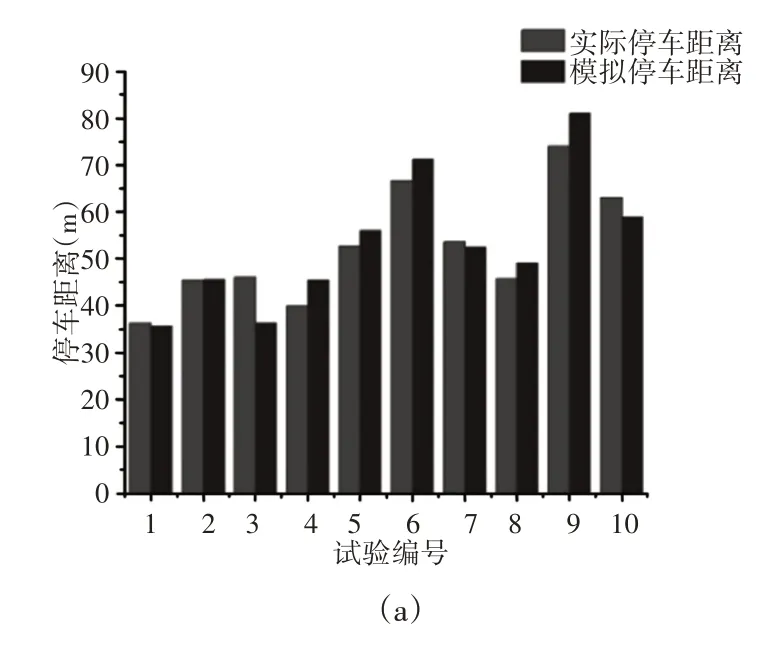
表4 车轮离散元颗粒参数Tab.4 Parameters of Tire Discrete Element Particles

如图8所示，展示了1失控车辆在制动床上减速时，车轮沉陷深度的变化。随着停车距离的增大，车轮沉陷深度也相应增大。

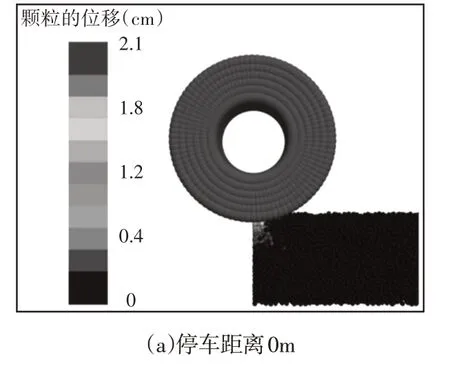
图8 不同停车距离时的车轮沉陷过程Fig.8 Tire Subsidence Process at Different Stopping Distances

3.3 悬架系统的影响

以往研究假设平衡状态下车身对车轮的作用力恒定不变，忽略了车辆悬架系统K&C特性对车轮减速过程的影响。失控车辆在实际的减速过程中，由于受到悬架系统的影响，车身作用在车轮上的力是不恒定的。采用单轴自卸车进行仿真试验，驶入初速度为17.7m/s，制动床坡度为0。对比有无悬架作用时于车轮上的垂直作用力和车轮沉陷深度结果示意图，如图9、图10所示。

图9 有无悬架作用时的车轮垂直作用力比较Fig.9 Comparison of Vertical Force of Tire with or without Suspension

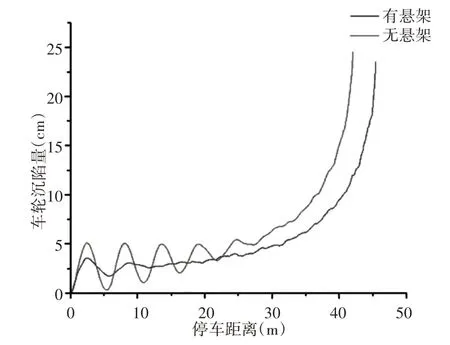
图10 有无悬架作用时的车轮沉陷深度比较Fig.10 Comparison of Tire Subsidence Depth with or without Suspension

从图9看出，车轮上的作用力在平衡力附近上下波动，在失控车辆驶入制动床的瞬间，车轮承受的作用力波动幅度最大。从图10看出，车轮沉陷深度由于悬架的影响波动较小，这主要是由于悬架K&C特性会改善系统的振动，导致车轮振动减小，沉陷波动减小。失控车辆减速过程的能量消耗主要来自砾石的阻力，悬架系统阻尼的耗能比砾石阻力要小很多，故悬架-车轮-集料三维模型的车辆沉陷深度要小于车轮-集料二维模型，从而导致停车距离的增加。由此可知，悬架系统影响作用在车轮上的作用力、车轮在减速过程中的沉陷深度和停车距离。

4 数值模拟

为了研究不同砾石粒径、车轮载重、驶入初速度对避险车道制动床上失控车辆车轮沉陷深度的影响，结合我国道路条件和车辆行驶状况，设计相应的试验方案开展数值模拟方案，如表5所示。表5选定的3种砾石料径的范围均在美国AASHTO推荐的57级（2.36～37.5mm）粒径范围内［14］。表5中1～3组的试验目的是研究砾石粒径的影响，4～6组的试验目的是研究车轮载重的影响，6～9组的试验目的是研究驶入初速度的影响。车轮沉陷深度模拟结果，如图11所示。

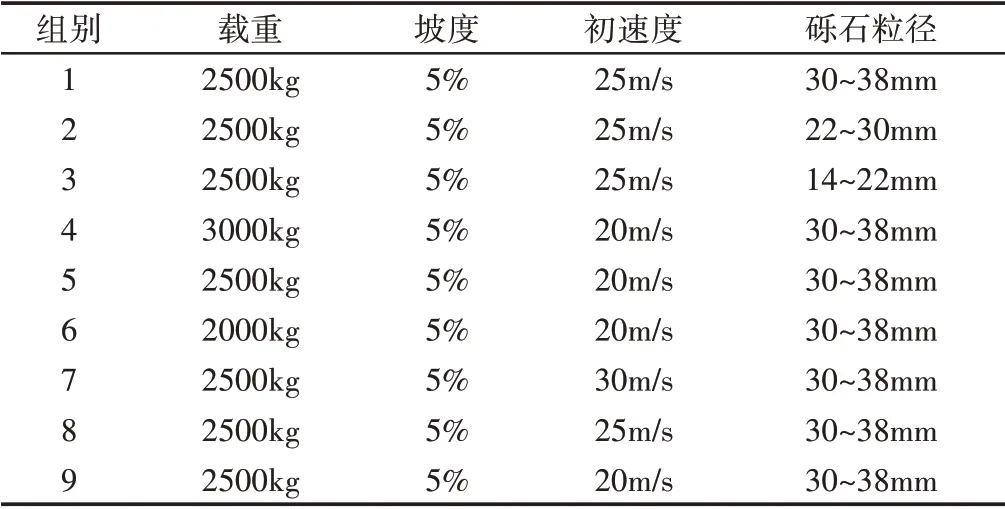
表5 数值模拟试验方案Tab.5 Plan of Numerical Simulation Test

从图11看出：（1）图（a），在相同的载重与初速度条件下，当停车距离一定时，粒径越小，车轮沉陷深度越大；（2）图（b），在相同的砾石粒径与初速度条件下，当停车距离一定时，车轮载重越大，车轮沉陷深度越大；当车轮沉陷深度一定时，（3）图（c），在相同的砾石粒径与载重条件下，当停车距离一定时，车辆初速度越小，车轮沉陷深度越大。

以上结果表明：砾石粒径、载重、初速度对车轮沉陷深度有显著影响。车轮沉陷深度增大会导致车轮与砾石颗粒的接触面积增大，车轮受到的阻力增加，车轮的动能消耗变快，导致停车距离减小。图11（b）中，单个车轮在载重为3000kg（严重超载）的情况下，最大沉陷量为40cm，在实际中，会有多个车轮碾过同一车辙，并且考虑到制动床在使用过程中因维护不当出现板结现象，建议制动床铺设厚度为80cm。《新理念公路设计指南》推荐避险车道长度设计时货车的驶入初速度可取100km/h和110km/h［15］。图11（c）中，粒径为（30～38）mm，车辆车速为108km/h（30m/s）时，最终的停车距离为120m。为了确保避免失控车辆冲出避险车道的终端，建议避险车道制动床长度≥140m。

图11 车轮沉陷深度数值模拟结果Fig.11 Numerical Simulation Results of Tire Subsidence Depth

5 结论

基于离散元方法，利用用悬架-车轮-集料三维离散元模型开展避险车道制动床上失控车辆车轮沉陷深度数值模拟，得出以下结论：（1）三维模型由于考虑了车轮沉陷变形的影响，估算的停车距离精度高于二维模型，并且三维模型模拟的停车距离更加贴近实际情况。（2）由于悬架系统的影响，车身作用在车轮上的力并不恒定，会减少车轮在制动过程中的波动，影响车轮沉陷深度，并使失控车辆的停车距离增大，并且模拟的车轮沉陷深度也更加贴近实际情况。（3）鉴于车轮沉陷深度对停车距离的影响，在推荐的砾石粒径范围内，砾石粒径越小，车速越小，车轮载重越大，车轮就更容易陷入砾石集料中，车轮沉陷深度越大，减速效果越好，则停车距离越小。（4）为了保证较好的制动床制动效果，制动床铺设计厚度建议在80cm以上。在车速较高时，车辆有可能会冲出避险车道，建议避险车道设计长度≥140m。