内燃动车动力包刚柔耦合系统动力学特性分析

贾尚帅，王兴民，赵新利，黄 燕

（1.中车唐山机车车辆有限公司技术研究中心，河北 唐山 064000；2.西南交通大学机械工程学院，四川 成都 610036）

1 引言

内燃动车组运行不受地域限制，不需要为其铺设电网，成本较低，在使用中能够灵活编组，广泛应用在欧美、亚、非、拉等国家，在铁路运输领域占有着重要地位［1］。内燃动车采用动力分散设计的方式，采用柴油发电机组悬挂于车体下方作为动力源，受车下空间限制，设计中将柴油发电机组、空冷装置、静压泵以及其它附属装置共同集成在一个公用构架上，整个动力单元称为动力包。根据柴油机产生激励特性以及悬挂方式的影响，动力包振动具有激励振动频带宽，与设备产生多种耦合并存的特点，为减小机组振动，防止过大振动传至车体，避免动力包与车体产生耦合振动，影响旅客乘坐舒适性，目前动力包多采用双层隔振系统对振动加以控制［2］。

双层隔振设计研究中，根据对于研究的侧重点可以将振源、中间质量及基础视为刚体，这种简化方法能够表现系统的主要特征，忽略其在激励作用下产生的变形，能够保证一点的隔振效果情况下加快研发速度［3-4］。随着经济发展，内燃动车为了提高运行速度，增加载重水平，采用了轻量化设计的方法，这种设计方法导致结构刚度降低，隔振系统中中间质量以及基础的柔性问题导致的结构振动不容忽视，这类结构振动问题已经在其他机械结构上得到了重视［5］。对于双层隔振系统的研究中，文献［6］对于某型内燃动车动力包的双层隔振系统进行了仿真和实验研究，研究表明测量结果比多刚体的集中质量模型结果偏大，初步提出可能是发生了部件间的振动耦合有关。文献［7-8］通过仿真的方法研究了构架柔性对于双层隔振系统传递特性的影响，进一步证实了整机振动与部件间的耦合关系。文献［9］建立了一种包含设备、隔振器、筏架和基础的全柔性浮筏双层隔振系统的动力学模型，通过数值算例验证了模型的正确性，并讨论了筏架刚性与柔性对隔振效果的影响。文献［10］对于刚性板和弯曲梁组成的双层隔振系统研究了在传递路径中加入周期性结构机械滤波装置来减少基础共振时产生的振动。文献［11］在建模当中只考虑隔振器沿着中轴垂向力的传递，将隔振器建模成为一维连续杆，浮筏建模成为梁，被隔振激励源建模成为集总力矩，基础被看成板，采用传递矩阵法、有限元法建立了双层柔性浮筏系统模型研究周期结构机械滤波器对于双层浮筏系统中隔振效果的影响。目前对于双层隔振系统的研究主要考虑部分柔性化处理之后对于整体隔振性能的讨论，通过改变隔振参数或者增加隔振元件的方法改善传递路径的基本特征，来达到优化设计的方法。

从现有研究工作来看，对于双层隔振系统柔性化后的隔振设计一直是研究的重点与难点。现有的研究中为了突出柔性化处理对于双层隔振系统的影响，忽略了空冷、静压泵等子系统对双层隔振系统动力学特性的影响。以某带双子系统的内燃电传动车组动力包为研究对象，分别建立24自由度多刚体系统动力学模型以及考虑中间构架柔性的刚柔耦合系统动力学模型。通过实验验证模型的准确性，对其自由振动和强迫振动结果进行分析，探讨中间构架柔性对双子系统的双层隔振系统振动特性的影响规律。研究结果对于指导中间构架及动力包双层隔振系统的优化设计具有一定参考价值。

2 动力包双层隔振系统动力学建模

2.1 多刚体动力学模型

对于某悬挂在内燃动车车体下方动力包进行建模，动力总成采用柴油发电机组（本机组为最低工作转速为900r/min，最高转速为1800 r/min的6缸直列柴油机）、空冷装置、静压泵、进气滤清器、排气消音器、膨胀水箱以及各系统之间的连接管路共同集成在一个公用构架上。动力包结构示意图，如图1所示。考虑动力包中机组、构架、空冷和静压泵作为主要的质量单元，由于其他装置质量小，刚性连接在公共构架上，因此考虑成为构架上的质点。将包含子系统的动力包双层隔振系统可以简化为多自由度系统动力学模型，如图2所示。采用文献［12］中的方法，以柴油发电机组的质心为系统参考坐标系的原点，建立含空冷与静压泵子系统的双层隔振系统24自由度的集中参数模型。

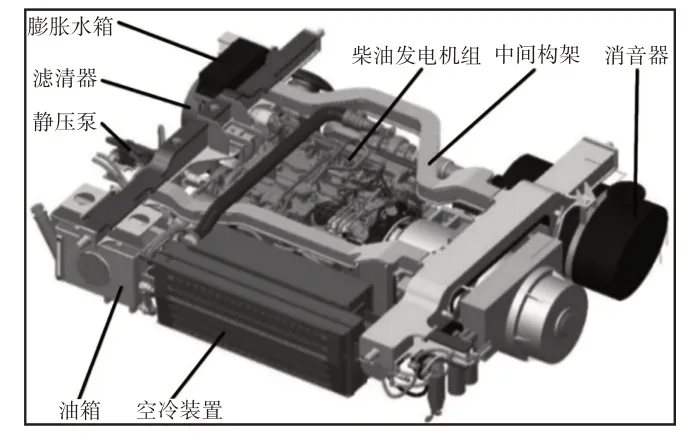
图1 动力包结构示意图Fig.1 DMU Schematic

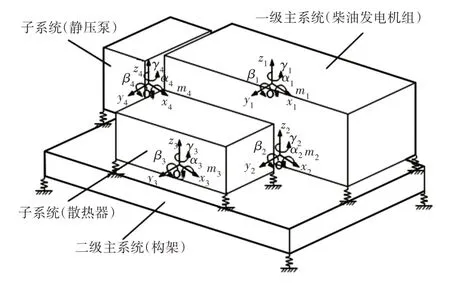
图2 含双子系统的双层隔振系统动力学模型Fig.2 Dynamic Model of the Double-Layer Vibration Isolation System with Dual Subsystems

2.2 ANSYS与ADAMS联合仿真刚柔耦合模型

为和多刚体模型相互验证，软件建模中同样考虑动力包中机组、构架、空冷和静压泵作为主要的单元，忽略刚性连接在构架上的装置影响，根据中间构架结构参数，利用Pro/E三维建模软件建立中间构架的三维模型，采用ANSYS与ADAMS进行联合仿真，构建中间构架的刚柔耦合模型。研究过程中屏蔽了中间构架500Hz以后的模态，这样可以在保证计算精度的前提下，提高计算效率。研究过程中视车体为无限大刚体。创建好的动力包双层隔振系统刚柔耦合动力学模型，如图3所示。

图3 动力包刚柔耦合系统动力学模型Fig.3 Dynamics Model of the Rigid Flexible Coupled DMU System

3 系统模态特性分析

3.1 模型实验验证

为了进一步验证模型的准确性，对动力包双层隔振系统进行了模态测试。实验参照《机械导纳的试验确定：第2部分用激振器作单点平动激励测量》（GB/T 11349.2-2006/ISO7626-2：1990）等相关标准。实验系统由加速度传感器、信号采集仪、计算机和专业分析软件等组成，实验系统，如图4（a）所示。将被测试动力包安装在实验台架上，按照实验大纲要求，在动力包上选取23个测点（其中构架12个，机组7个，空冷装置4个），分别安装3向加速度传感器。实验过程中使用激振器对系统施加正弦激励，采集激振力信号和各测点振动加速度响应信号，如图4（b）所示。在激振器激励作用下，系统产生振动响应，采集响应点三个方向的振动加速度信号。

图4 动力包模态测试示意图及测试现场照片Fig.4 Schematic of DMC Modal Test and Test Site

动力包试验模态对应频率与多刚体系统动力学模型、刚柔耦合系统动力学模型计算模态对应频率对比，如表1所示。该简谐激励能激起如下有效的模态频率：3.56Hz、5.21Hz、6.27Hz、7.31Hz、30.50Hz、33.74Hz。可以看出，相对于多刚体系统动力学模型，刚柔耦合系统动力学模型模态计算结果与试验结果更接近，相对误差在15%以内，模型满足建模精度要求。

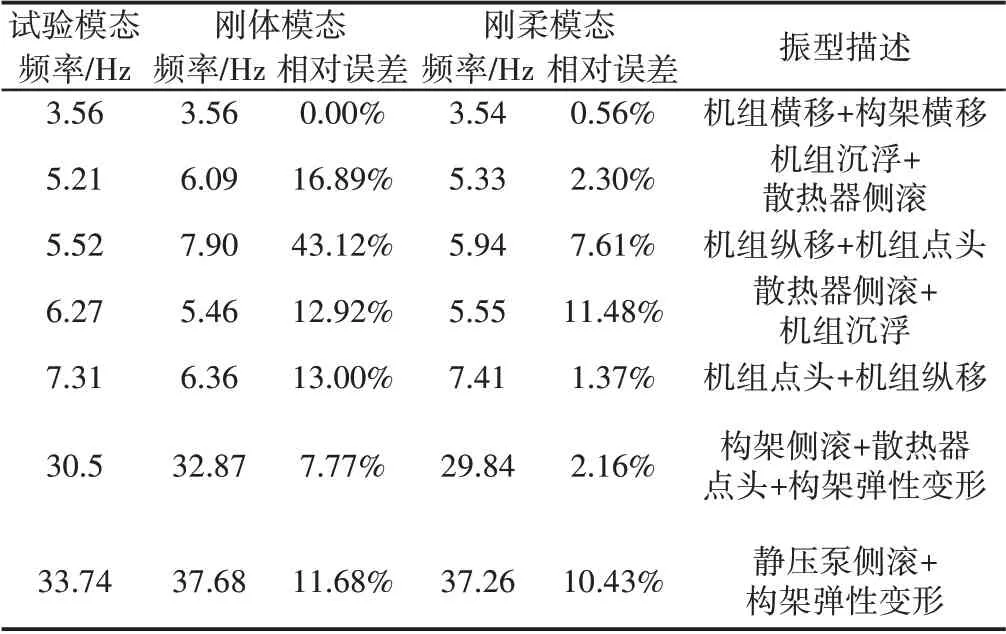
表1 计算模态与试验模态对比Tab.1 Comparison Between Computational Modes and Experimental Modes

3.2 模态特性分析

根据两种动力学模型，利用自由振动计算结果，可定性讨论构架柔性对系统模态特性的影响。刚体动力学模型计算的24阶模态能量分布情况见附表1，其中x，y，z，α，β，γ分别表示部件在图2所示参考坐标系中的纵向、垂向、横向、横摇、平摇、纵摇六个自由度振动，机组、构架、空冷和静压泵模态的标号分别为1、2、3、4。刚柔耦合系统动力学模型的模态能量分布情况见附表2。

从附表1和附表2可以得到，可以得出各部件与构架结构振动耦合模态的振动频率和能量分布情况，其中附表2中第25、26阶是构架结构振动与动力包刚体振动相耦合的模态，构架结构振动能量分别是26.97%、39.77%，第27-30阶是构架结构振动为主的模态，振动能量分别是94.68%、93.26%、97.68%、97.65%。第25行表示各阶模态对应的构架结构振动模态能量。

根据本动力包的振动特性，采用的柴油发电机组是主要的激励源，激振力主要包括柴油机倾倒力矩、往复惯性力（矩）、离心惯性力（矩）以及主发电机因转子不平衡质量产生的离心惯性力。本机组采用直列6缸柴油机，倾倒力矩以3.0谐次和6.0谐次为主。激励频率与柴油机转速有关，本机组最低工作转速为900r/min，最高转速为1800r/min，激振力频率最低为15Hz，最高为180Hz。

附表1多刚体系统动力学模型模态能量分布计算结果Appendix Tab.1 Calculation Results of Modal Energy Distribution of Multi-Rigid System Dynamics Model

附表2刚柔耦合系统动力学模型模态能力分布计算结果Appendix Tab.1 Calculation Results of Modal Capacity Distribution of Dynamic Model of Rigid-Flexible Coupled System

机组和构架各阶模态固有频率与主要激励频率的模态匹配情况由图5所示，无论是多刚体系统动力学模型，还是刚柔耦合系统动力学模型，机组的各阶模态固有频率，都在15Hz以下。而机组的激励频率在15Hz以上，因此不会引起强烈共振，激振频率位于在机组各阶模态振动响应较为稳定的过共振区。另外，从刚柔耦合系统动力学模型计算结果还可看出，机组各阶模态的结构振动能量最大仅有0.58%，即构架结构振动几乎不与机组各阶模态产生耦合，构架柔性对机组整机振动影响很小。因此对于柴油发电机组，两种模型的整机振动响应情况差别很小。

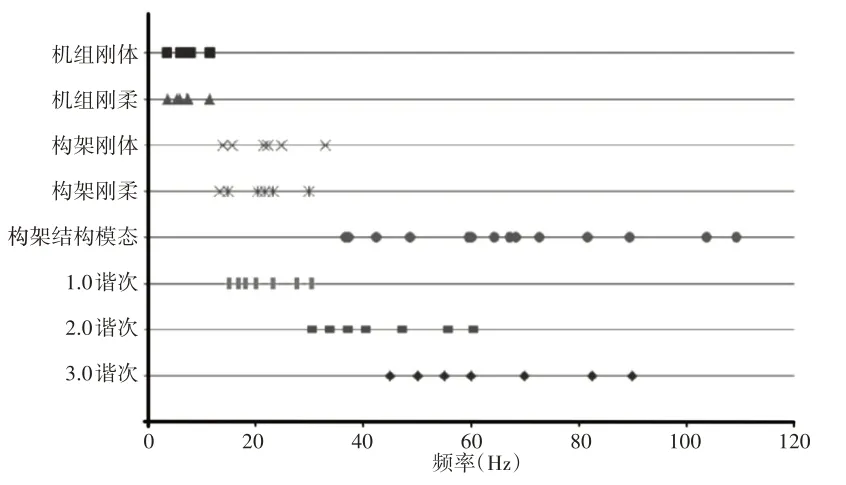
图5 机组和构架固有频率与激励频率的模态匹配图Fig.5 Modal Matching of Natural Frequency and Excitation Frequency of Unit and Frame

构架各阶振动模态与主要激励频率匹配关系则较为复杂，两种模型各阶模态频率和振型的不同，都有可能影响构架的振动响应情况。首先，在惯性力激振频率范围内，两种模型各阶模态固有频率存在的差别，会改变各激励频率与各模态固有频率的接近程度，使各激励频率处的振幅放大系数出现变化：其次，刚柔耦合系统动力学模型会产生构架刚体振动与结构振动的耦合，如23.19Hz的x2模态有8.13%的构架结构振动能量，29.84Hz的α2模态有15.69%的构架结构振动能量，构架结构振动模态的出现会影响构架上各点的振动响应：最后，刚柔耦合系统动力学模型除了24阶整体振动模态外，还增加了多阶结构振动模态，也可能增大振动响应幅值。

4 系统响应特性分析

通过对多刚体和刚柔耦合系统动力学模型进行谐响应分析，定量研究中间构架柔性对动力包双层隔振系统振动响应特性的影响规律。考虑到该动力包的主要激振力为倾倒力矩，在倾倒力矩作用位置输入（0～200）Hz的扫频简谐激励。在机组和中间构架、以及二级隔振器位置布置测点计算速度响应。

两种模型的机组振动测点处垂向速度的扫频响应曲线，如图6所示。其中，实线代表刚体模型计算结果，虚线代表刚柔耦合模型计算结果。研究结果表明：考虑构架柔性的刚柔耦合模型包含了刚体振动模态，柔性处理导致等效刚度降低，机组峰值响应也相对于多刚体状况存在略微降低：但相应的构架柔性化处理对应模态的响应幅值变化并不明显。特别是在15Hz之后，两种模型下机组振动测点处垂向速度的响应曲线基本重合，这意味着对于该激励频率在15Hz以上的柴油发电机组，两种模型的机组整机振动响应差别很小，构架柔性对机组整机振动影响很小。

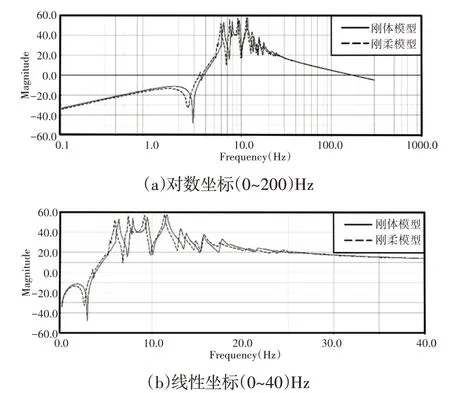
图6 机组振动测点处的速度扫频响应曲线Fig.6 Speed Sweep Response Curve at the Unit Vibration Measuring Point

两种模型的中间构架振动测点处垂向速度的扫频响应曲线，如图7所示。研究结果表明：构架柔性化处理依然能够保留两种模型的刚体模态，但是构架的部分刚体模态和构架自身产生的结构振动耦合在了一起，改变了系统的固有频率以及振动响应的情况。首先，构架峰值响应也相对于多刚体状况存在略微降低，这与机组的峰值响应相同，都是由于等效刚度降低造成的固有频率下降，这个特性伴随整个振动响应。其次，构架的柔性化处理使构架在（20～40）Hz的频段中刚柔模型相比于刚体模型出现了新的振动响应情况，经过与文献［7］的构架实验模态对比，发现是振动响应与中间构架的扭转、菱形模态发生了相互耦合，导致了响应的波动。另外，由于固有频率的差别，导致高阶频率下激振力同系统共振特性发生了更明显的差距。对于40Hz频段，激励频率远高于隔振系统的固有频率，因此多刚体模型已经没有共振响应，但由于构架的柔性化处理导致了系统增加了多个响应峰值，这是由于激励与构架的结构模态发生了耦合导致的多个振动响应情况，符合模态特性中的结构振动能量占比大于90%的结果。

图7 中间构架振动烈度测点处的速度响应Fig.7 Velocity Response at the Vibration Measuring Point of the Intermediate Frame

研究表明，构架上任意点的振动响应是一定激励下所有刚柔耦合振动模态响应的叠加，在低频段中间构架柔性对系统刚体模态影响很小：在（20～40）Hz会产生部分构架刚体振动与结构振动的耦合，但这种耦合仍是以构架刚体振动模态为基础进行的，只有两个耦合模态的结构振动能量稍大，结构振动能量占比分别是15.69%和8.13%，因此两种模型的振动响应曲线总体上变化趋势相同、幅值相近、相互交错：在40Hz以上则为相对独立的中间构架结构振动模态，振动响应曲线是构架结构振动响应曲线在刚体振动过共振区响应曲线基础上的叠加。综上所述，考虑构架柔性后，构架上的振动响应仍是以刚体振动模态响应为基础，多刚体系统的振动响应基本决定了刚柔耦合系统响应的变化趋势和大概波动范围。所以，目前使用的首先将机组、中间质量以及基础视为刚体进行隔振优化设计，再建立刚柔耦合模型校验和调整的隔振设计策略是合理且可行的，既有很高的优化设计效率又能保证隔振效果。

5 结语

对于某内燃动车带双子系统的动力包双层隔振系统进行了中间构架柔性对于隔振系统基本模态特性以及动力学响应影响的研究，结论如下：

（1）中间构架柔性化处理导致系统等效刚度减小，使机组整机振动模态固有频率左移的情况，对应模态的响应幅值变化不明显。在15Hz之后，构架柔性对机组振动速度幅值影响不大，因此对于该激励频率在15Hz以上的机组，构架柔性对机组整机振动影响很小。

（2）频率较低（40Hz以下）的结构振动模态会与部分构架刚体振动模态耦合，使相关耦合模态的固有频率及响应幅值发生一定变化：频率较高（40Hz以上）的构架结构振动模态，为相对独立的构架结构振动模态，与动力包各部件刚体振动模态基本没有耦合。

（3）考虑构架柔性后，构架上的振动响应仍是以刚体振动模态响应为基础，多刚体系统的振动响应基本决定了刚柔耦合系统响应的变化趋势和大概波动范围。在（20～40）Hz两种模型的振动响应曲线总体上变化趋势相同、幅值相近、相互交错，在40Hz以上刚柔耦合系统振动响应曲线是构架结构振动响应曲线在刚体振动过共振区响应曲线基础上的叠加。

该研究对于动力包中间构架的设计具有重要的指导意义，将结构振动影响考虑到双层隔振系统中，对于进一步提高隔振效果具有一定的借鉴意义。