PHEV驱动模式切换的分阶段子控制器协调控制

樊永强

（广东省交通运输技师学院，广东 广州 501520）

1 引言

混合动力汽车作为严重非线性机电系统，在应对频繁启停、载荷变化和坡度变化时，会导致动力源间频繁的发动机启停、电机启停、离合器抱合与分开控制等，频繁的工作模式切换带来的冲击会严重影响乘坐舒适度和车辆驾驶寿命［1］，因此研究切换瞬态冲击控制方法意义重大。

针对并联式混合动力汽车模式切换过程中的瞬态冲击控制问题，当前已经存在一些成果。文献［2］使用模型参考控制方法协调控制模式切换，实现了降低冲击度同时减小离合器滑磨功的效果；文献［3］使用μ理论设计了鲁棒控制器，通过跟踪车轮转速补偿转矩波动；文献［4］将离合器滑磨功和模式切换冲击度为优化目标，将控制问题转化为最优控制问题，使用极大值原理和二次型最优控制原理设计了模式切换控制器；文献［5］结合驾驶意图，将踏板深度和变化率转化为离合器结合时长，使用动态规划分配汽车转矩，补偿了切换时的转矩波动。总的来讲，要想实现模式切换过程中的快速、平滑过渡，发动机、电机、离合器间协调控制是需要解决的关键问题。

针对混合动力汽车在驱动模式切换过程中冲击度较大的问题，将切换过程划分为3个子阶段，根据各阶段动力源特点和控制目标设计控制器，同时给出了子控制器的切换条件，最终达到了减小车辆冲击度的目的。

2 PHEV简介与协调控制策略

2.1 PHEV动力总成系统

并联式混合动力汽车（Parallel Hybrid Electric Vehicle，PHEV）动力总成系统，如图1所示。主要由动力系统和传动系统组成。动力系统包括发动机及其控制单元ECU、ISG电机及其控制器、动力电池及其管理系统BMS。传动系统包括变速器、减速器、耦合装置等。整车控制器是车辆能量管理的中枢，控制各动力源的输出转矩、离合器开合等。

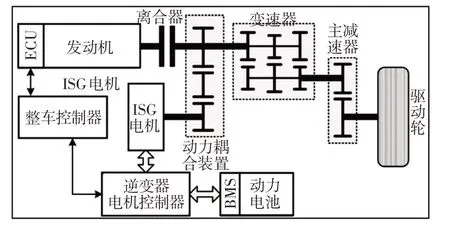
图1 PHEV动力总成系统Fig.1 Powertrain System of PHEV

PHEV工作模式包括发动机单独驱动模式、纯电动驱动模式、联合驱动模式、行车发电模式和再生制动模式［6］，当模式之间进行切换时，由于电机和发动机的动态特性差异性较大，导致在切换时的转矩冲击较大。以纯电动驱动向联合驱动模式切换过程中的转矩冲击控制为研究课题。

2.2 协调控制策略

在混合动力汽车由纯电动驱动向联合驱动切换过程中，按照离合器的接触状态将切换过程划分为3个阶段，为离合器分离阶段、离合器滑磨阶段和离合器接合阶段。离合器分离阶段向滑磨阶段切换的条件为 ||Δω＜20rmin，式中：Δω—离合器两端转速差；滑磨阶段向接合阶段切换的条件为ωe=ωmig，式中：ωe—发动机转速；ωm—驱动电机转速；ig—变速器传动比。

离合器分离阶段：当达到模式切换条件时，ISG电机除提供车辆行驶动力外，还需提供发动机启动转矩，直到加速至点火转速（800r/min）；待离合器主从动盘转速差值满足条件时切换至离合器滑磨阶段。在离合器分离阶段，当离合器两端转速差较大时，为避免车辆通过增加喷油量减小转速差而导致油料燃烧不充分、排气中有毒气体增加的问题，因此必须对发动机转速进行控制。

离合器滑磨阶段：在离合器滑磨阶段，发动机依然使用上一阶段控制方法进行转速调节，而滑磨阶段由于发动机动力的非线性参与及扰动转矩作用下，导致动力系统输出转矩的突变。为了减小转矩突变，参考电机动态响应快的特点，使用滑模控制对电机转矩进行调节。离合器接合阶段：由于电机与发动机动态响应差异性，为防止动力系统输出转矩出现突变，此阶段依然使用滑模控制调节电机转矩，直至发动机完全渡过动态响应过程。按照以上分析，PHEV在3个阶段的控制对象和控制目标不同，因此这里提出了多子控制器切换的协调控制方法，子控制器的切换条件与各阶段的切换条件一致，如图2所示。

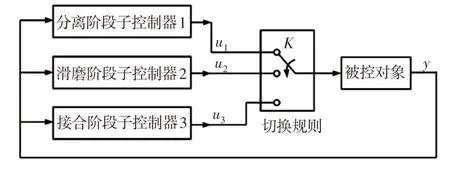
图2 协调控制器Fig.2 Coordinated Controller

3 子控制器设计

本节对离合器分离阶段、滑磨阶段、接合阶段子控制器分别进行设计。

3.1 分离阶段子控制器

在离合器分离阶段，以离合器两端转速误差为被控制量，以发动机喷油量为控制量，防止喷油量过大而产生燃油不充分燃烧现象，为了实现上述控制目的，设计了智能算法整定PI参数的分离阶段子控制器，如图3所示。

图3 智能算法整定参数的PI控制器Fig.3 PI Controller Parameters Optimized by Intelligent Algorithm

定义离合器两端转速差Δω=ωmig-ωe，则k时刻控制量为u(k)=kp·Δω(k)+ki·[ ]Δω(k)-Δω(k-1)，式中：kp、ki—比例系数、积分系数。PI系数一般人为设定，过度依赖个人经验，这里使用粒子群算法进行参数整定，解决参数设置的盲目性和随机性问题。粒子群算法根据鸟群中的最优个体和历史最优位置对搜索速度和位置进行更新，算法原理可参考文献［7］，这里不再介绍，仅对粒子编码方式和目标函数进行明确。

由于含有两个待优化系数，因此将粒子维度设置为2，粒子使用十进制编码方式。参数优化的目标函数为：

3.2 滑磨阶段子控制器

在离合器滑磨阶段，由于发动机力矩高度非线性参与到动力系统中，使得动力系统输出力矩发生突变，为了减小力矩突变，设计了自适应滑模控制器对驱动电机力矩进行控制。

（1）构造滑模面。在离合器滑磨阶段，驱动电机的动力学方程为：

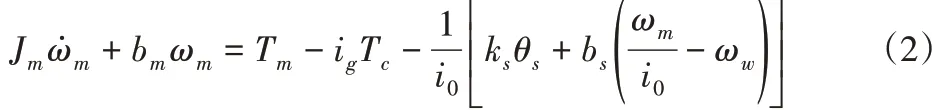
式中：Jm—驱动电机折算到车轮上的转动惯量；ωm—驱动电机转速；bm—驱动电机阻尼系数；Tm—驱动电机输出转矩；Tc—离合器传递转矩；i0—主减速器的速比；ks—驱动桥刚度；θs—驱动桥角位移；bs—驱动桥阻尼系数；ωw—车轮转速。

将外部干扰、建模误差、参数摄动等统一为干扰项d，且有||d＜D，D为干扰项上界。此时可将驱动电机的动力学方程改写为：

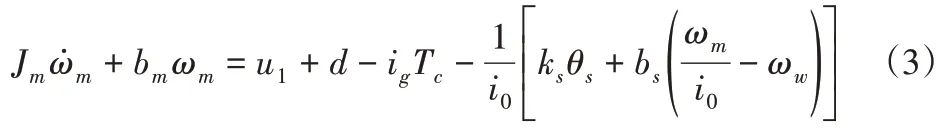
式中：u1—使用滑模控制设计的控制律。

驱动电机实际转速ωm的期望轨迹ωmd可由车轮转速换算得到，定义滑磨阶段的电机转速跟踪误差为e1(t)=ωm(t)-ωmd(t)。选择驱动电机转速为状态变量x，即x=ωm；同时将驱动电机转速作为输出量y，即y=x，则式（3）对应的状态空间方程为：

式（4）所示系统的相对阶为1，因此构造滑模面为：

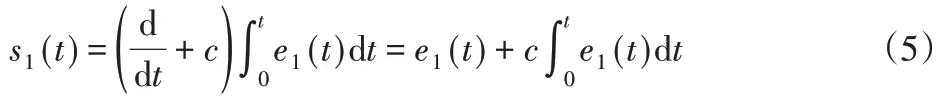
式中：c＞0—一个常数。

（2）设计控制律。滑模控制律u1由等效控制律u1eq和变结构控制律u1vss组成，等效控制律控制状态点在滑模上向原点滑动，变结构控制律控制状态点由任意位置向滑模面滑动［8］。当系统状态在滑模面上运动时有s˙1=0，对式（5）求导，并将式（4）代入，得：

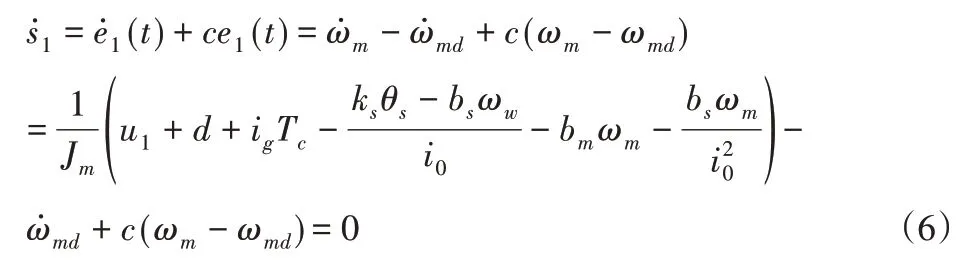
由此得到等效控制律u1eq为：

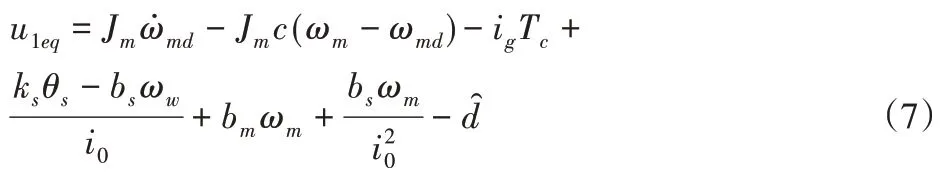
为使系统在任意状态时向滑模面运动，常用变结构控制律为：

式中：κ＞0—一个常数，sgn()为符号函数。若要求系统状态以趋近速率η等速率向滑模面运动，应满足ss˙≤-η||s，η＞0，结合式（6）可知：

为了达到要求的趋近速率η，需满足κ≥Jmη，后文进行仿真和实验时取κ=Jmη。为了削弱滑模控制的抖振现象，实验连续函数θ(s1)代替非连续的符号函数sgn(s1)，为：

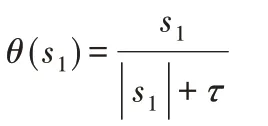
式中：τ—极小的正常数，防止分母为0。

则变结构控制律和滑模控制律为：

（3）干扰项d在线估计及稳定性分析。干扰项的存在使得系统状态无法按照设定轨迹向滑模面运动或者需要更大功率才能够向滑模面运动，因此需要对干扰项进行在线估计。RBF神经网络是以函数逼近理论为基础构造的单隐含层神经网络，由于其对非线性函数具有无限逼近能力，这里使用RBF神经网络在线估计干扰项。

选择神经网络输入向量为X=[ωe，ωm，Fc]，其中Fc为离合器盘片的压紧力，根据RBF神经网络原理，干扰项估计值为：

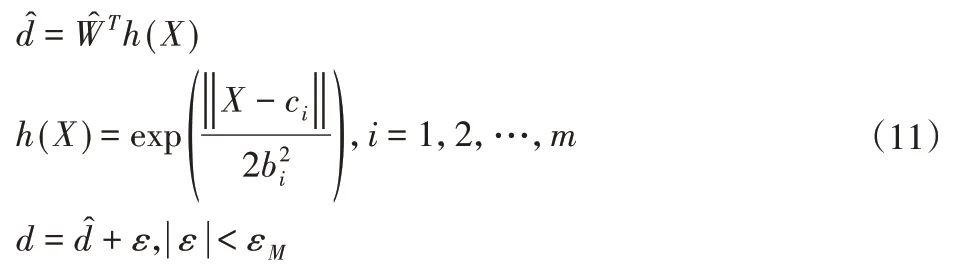
定义李雅普诺夫函数为：

对式（12）求导，得：

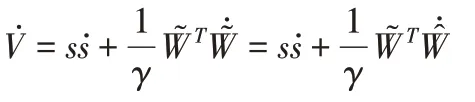
将式（4）（9）（11）代入上式，整理得：

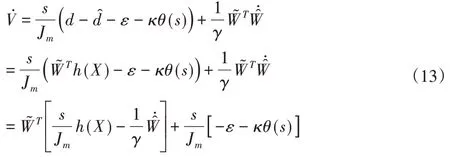
同时式（13）转化为：

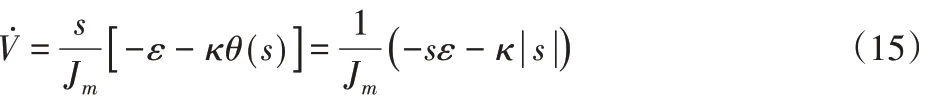
此时只需保证κ取值时有κ＞εM，就可以保证V˙＜0。另外根据Barbalat定理有则自适应滑模控制器具有李雅普诺夫稳定性，可以使误差在有限时间内运动至零点。

3.3 接合阶段子控制器

在离合器接合阶段，发动机和驱动电机均参与力矩输出，但是由于发动机动态响应过程较驱动电机缓慢，因此必然出现动力系统输出力矩的突变，这里依然使用自适应滑模控制器对电机转矩进行控制。在离合器接合阶段，驱动电机动力学方程为：

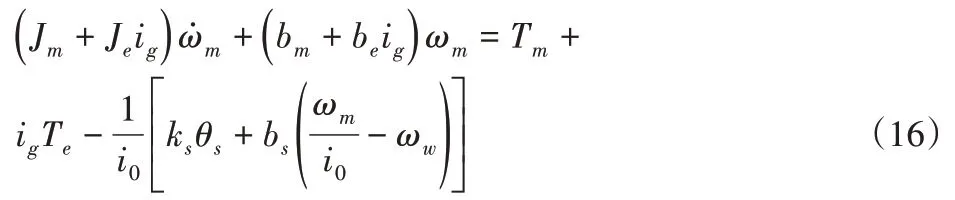
式中：Je—发动机转动惯量；be—发动机阻尼系数；Te—离合器传递矩阵。

引入干扰项d′和接合阶段的滑模控制律u2，将式（16）转化为：

与3.2节滑模面的构造、控制律的设计、干扰项在线估计的方法完全一致，过程不再重复，仅给出滑膜面、控制律及干扰项估计结果如下所示：

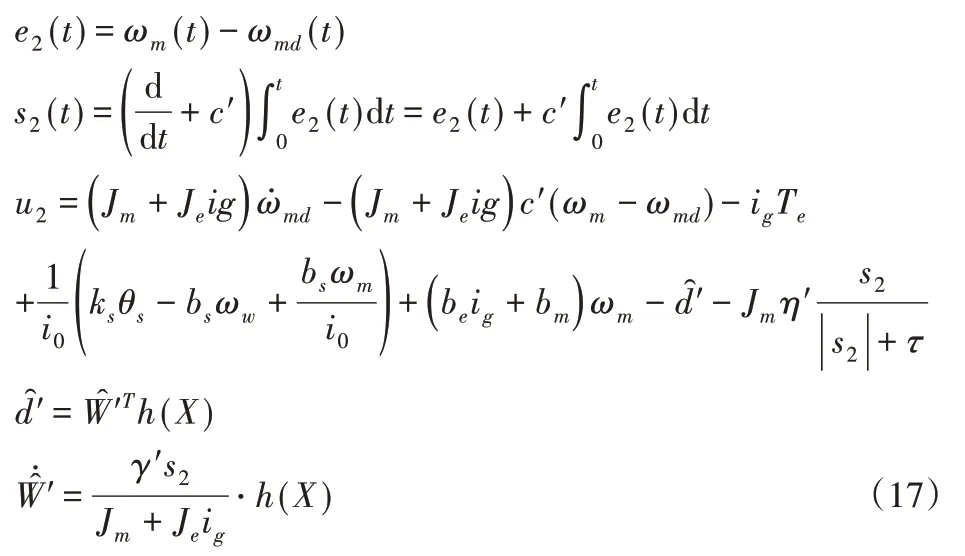
根据3.2节对可调节参数的推导过程可知，在满足有κ′＞εM的条件下，式（17）给出的自适应滑模控制器具有李雅谱诺夫意义下的稳定性，误差可在有限时间内收敛至零点。

4 仿真验证与分析

4.1 仿真环境设置

为了对控制器的性能进行评价和比较，将车辆纵向冲击作为驱动模式切换品质的评价指标，冲击度计算方法为：

式中：J—车辆冲击度；ɑ—车辆加速度。

在Simulink中搭建并联混合动力汽车动力总成系统，包括动力电池模型、发动机模型、ISG电机模型、变速器模型和驾驶员模型等，搭建动力系统模型使用的数学模型见文献［10］，车辆的参数设置，如表1所示。

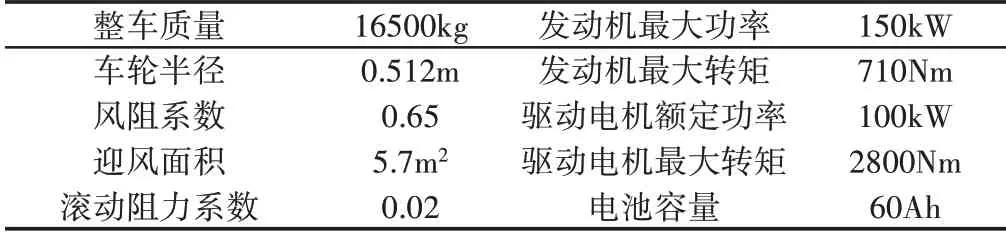
表1 车辆参数设置Tab.1 Parameters Setting of Vehicle

从中国典型城市公交工况（CCBC工况）中截取（130～155）s共25s的速度曲线作为测试工况，速度变化曲线，如图4所示。在142s时车速达到15km/h，达到了模式切换的车速阈值，开始进行驱动模式切换。

图4 期望车速曲线Fig.4 Expected Speed Curve

4.2 仿真结果及分析

为了形成对比效果，分别在未施加控制和施加协调控制两种情况下给出车辆动力系统输出力矩和车速情况，发动机转速变化情况，如图5所示。动力源输出转矩变化情况，如图6所示。车速变化情况，如图7所示。冲击度曲线，如图8所示。对比图5中驱动模式切换过程中发动机转速的变化情况，在没有施加协调控制时，发动机转速在切换过程中的波动较大（图中虚线圈出部分）；而在施加协调控制情况下，发动机转速在整个切换过程中的变化非常平稳，几乎没有波动现象，充分证明了参数整定PI控制器在发动机转速控制中的有效性。

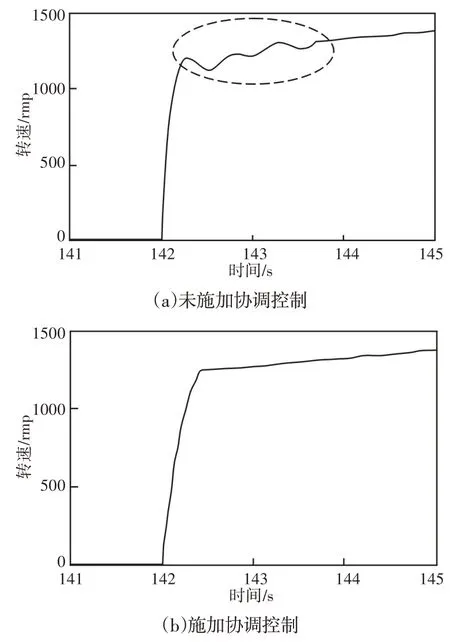
图5 发动机转速变化曲线Fig.5 Engine Speed Changing Curve

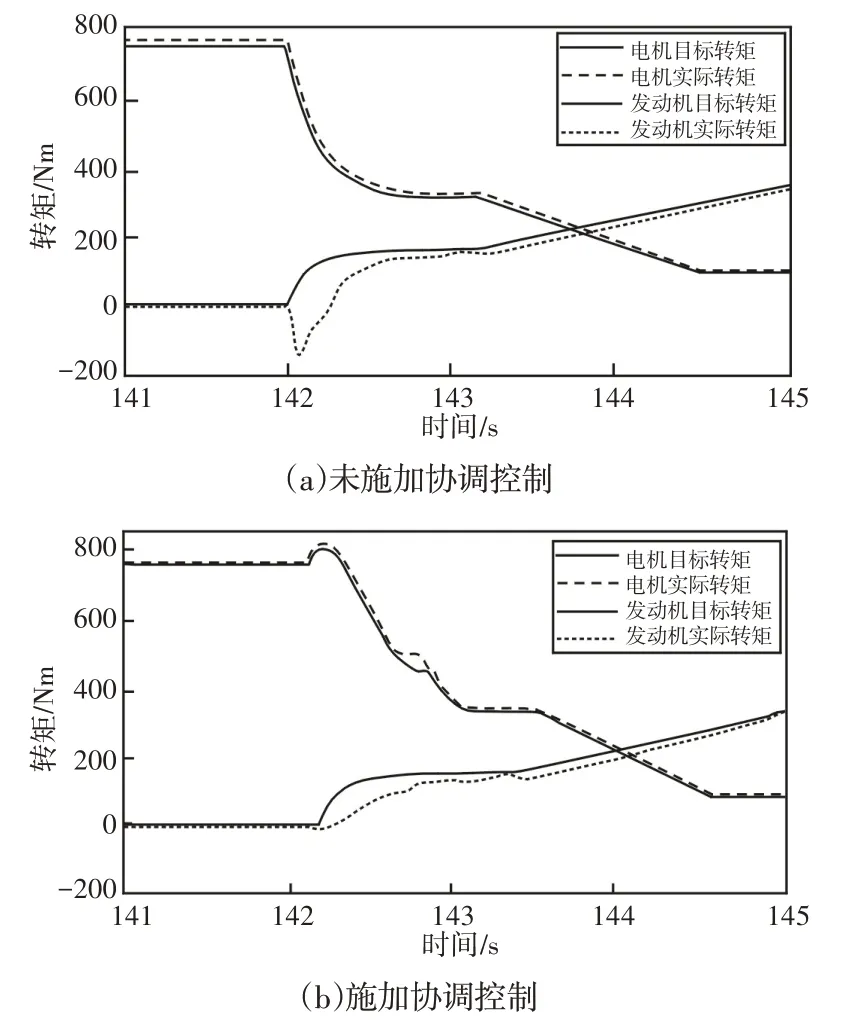
图6 动力源输出转矩Fig.6 Power Source Output Torque

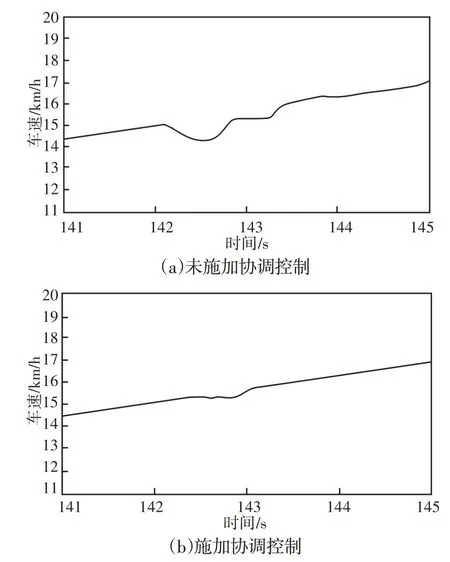
图7 车速变化曲线Fig.7 Speed Changing Curve

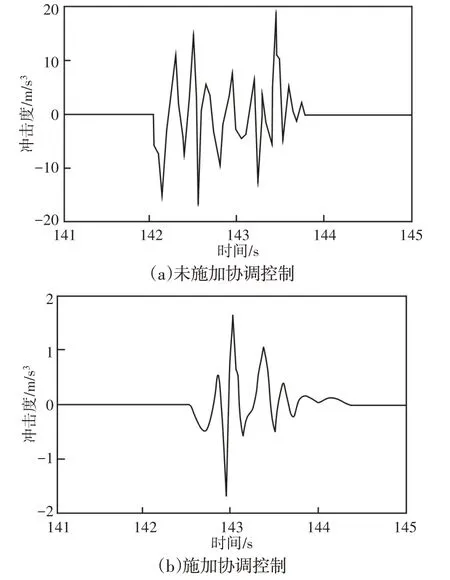
图8 冲击度变化曲线Fig.8 Degree of Jerk Changing Curve

对比图6中转矩变化情况，在整个模式切换过程中，施加控制时转矩误差明显小于未施加控制时，经统计未施加控制时转矩跟踪误差最大值为224.3Nm，而施加控制时转矩跟踪误差最大值为56.5Nm，这是因为使用自适应滑模控制器对电机转矩进行控制，同时实时在线估计各因素产生的干扰项d，使跟踪误差在有限时间内收敛至零点。

对比图7和图8切换过程中车速及冲击度变化情况，未施加控制时车速在（142～144）s期间车速波动较大，导致车辆冲击度较大，冲击度幅值为18.7m/s3，这是因为模式切换过程中，离合器滑磨阶段发动机力矩的非线性参与、发动机动态过程缓慢于电机动态过程两个因素共同引起的；而施加协同控制时，车辆在（142～144）s期间车速变化极小，车辆冲击度幅值为1.81m/s3，与不施加控制时减小了一个数量级，这是因为施加滑模控制时，对建模误差、参数摄动等引起的干扰项进行实时估计，减小了干扰项对控制精度的影响，同时滑模控制器设计的控制律以跟踪误差为控制对象，使误差在有限时间内收敛至零点，实现了对误差的有效控制，减小了车辆冲击度。

5 结论

针对车辆在驱动模式切换过程中，因不同动力源动态特性差别大而引起车辆冲击较大的问题，这里将切换过程划分为三个阶段，并分别设计控制器，根据验证得出以下结论：（1）参数整定PI控制器可以有效控制发动机转速，实现在切换过程中的平稳变化；（2）分阶段子控制器协同控制方法可以有效减小模式切换过程中的车辆冲击度，提高车辆驾驶舒适度。