抓基础 理题型 保5分

胡全勇

(西北师大育才学校)

二项式定理在2020年人教A版新教材中，被排在《选择性必修第三册》.它在整个高中数学中占比较低，不是高中数学重点教学内容，在高考命题中有时出现，有时不出现.2021年高考四套全国卷(全国甲、乙卷理科，全国新高考Ⅰ，Ⅱ卷)都没有命题出现，但北京卷、天津卷、浙江卷、上海卷(夏季高考)都有命题出现，因此在2022年高考中应该引起大家足够重视，虽然属于简单题，但是千万不能“大意失荆州”，做到稳拿5分.

(a＋b)n＝＋b＋…＋＋…＋(n∈N*)是二项式定理，右边的多项式是二项展开式，其中(k＝0，1，2，…，n)是二项式系数(特别需要强调的是，有关二项式运算时，要厘清二项式系数与所求系数的区别与联系，不能混为一谈)，将二项展开式中的第k＋1项，即n，k∈N*)称为二项展开式的通项(或通项公式).学好二项式定理，必须做到如下几点.

1 熟练运用通项公式求特定项

在运用通项公式求二项展开式的特定项(一般指展开式的常数项、x的几次方项、有理项)时，为了运算方便，常常将未知数是根式的项写成分数指数幂，未知数是分式的项写成负整数指数幂，二项式中间为减号时，将减号与第二项结合，这类试题是高考命题中二项式定理部分考查频率最高的内容.

1.1 求常数项

求常数项是与二项式有关的试题出现频率最高的一个知识点，基本方法一般为运用通项公式将展开式中的第k＋1项整理为系数与未知数两部分乘积的形式，然后令未知数的指数为零，得到相应的k值，从而写出该项，这即为所求常数项.

例1(2021年北京卷11)的展开式中常数项是________.

解析

(x3－展开式的通项公式为

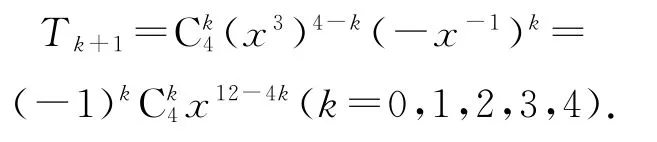
令12－4k＝0，则k＝3，故所求常数项为

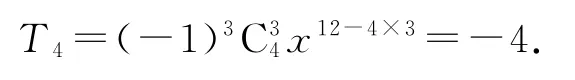
例2(2018年浙江卷理14)二项式的展开式的常数项是________.

解析

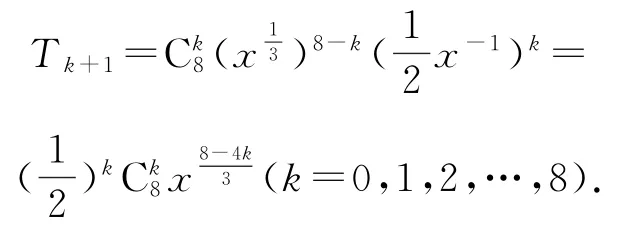
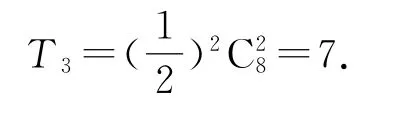
点评

这两道求常数项的题目，属于非常基础的题，也是高考的常见题型，求解要点是运用通项公式时按照要求运算.

1.2 求x的几次方项

求x的几次方项是与二项式有关的命题中比较常现的一个知识点，基本方法一般为运用通项公式将展开式中的第k＋1项整理为系数与未知数两部分的乘积，然后令未知数的指数为所求的未知数x的指数(如求x3项，就可以令未知数的指数等于3)，得到相应的k值，从而写出所求项(注意:有时求的是该项的系数).

例3(2021年上海卷6)(x＋a)5的展开式中，x2的系数为80，则a＝________.

解析

(x＋a)5的 通 项 公 式 为Tk＋1＝(k＝0，1，…，5).令5－k＝2，则k＝3，所以a3＝80，解得a＝2.

例4(2018年全国Ⅲ卷理5)的展开式中x4的系数为( ).

A.10 B.20 C.40 D.80

解析

令10－3k＝4，则k＝2，所以展开式中x4的项为即x4的系数为40.故选C.

点评

这两道题均是通项公式的基本运用，属于基础题，要避免失分.

1.3 有理项问题

求有理项是与二项式有关的问题出现频率较低的一个知识点，求解的基本方法一般为运用通项公式将展开式中的第k＋1项整理为系数与未知数两部分的乘积，然后令未知数的指数为整数(这样的项，一般不只一项，需要分类讨论)，得到相应的k值，从而写出对应的项.

例5已知的展开式中，前三项系数的绝对值依次构成等差数列.

(1)证明:展开式中没有常数项;

(2)求展开式中的所有有理项.

解析

依题意可得n≥2，又因为前三项系数的绝对值依次构成等差数列，即

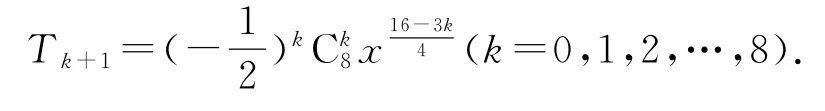
假设展开式中的第k＋1项为常数项，则0，解得，所以假设不成立，故这个展开式中没有常数项.

(2)由(1)可得求通项公式为则展开式中三项有理项，分别为

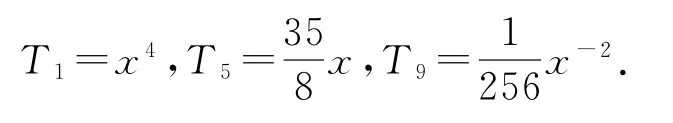
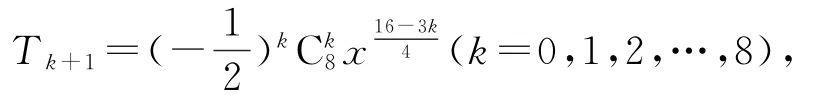
点评

展开式中的有理项是指未知数x的指数为整数的项，这个展开式中由于x的指数为所以求有理项时，k必须取4的倍数.

2 掌握三项式或两项乘积问题的运算技巧

2.1 三项式问题

1)底数为完全平方式

求底数为三项，并且底数为完全平方式的基本方法:将底数整理成一个完全平方式的形式，运用(an)m＝amn的运算法则，将底数整理成为两项，再运用二项式定理求解.

例6的展开式中x2项为_____.

解析

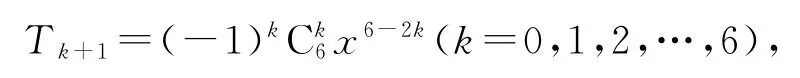
令6－2k＝2，则k＝2，故展开式中x2的项为

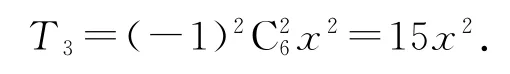
点评

解答这道题时注意两点:其一，底数是一个完全平方式;其二，求的是含有x2的项，而不是系数.

2)底数可以分解成两个因式乘积的形式

求底数为三项，并且底数可以分解成两个因式乘积的形式的基本方法:将底数分解因式后运用(ab)n＝anbn写成两个二项式的积，如果两项的指数不太高，可以直接将两个二项式展开，根据多项式乘法完成;如果两项的指数比较高，再分别根据二项式展开式的通项公式进行讨论，这样比较复杂.

例7(x2＋3x＋2)3的展开式中x4的系数为________.

解析

因为

所以展开式中含有x4的项为12x4，18x4，3x4，故展开式中x4的项系数为33.

点评

这道题底数可以分解成两个因式乘积的形式，所以问题可以转化为两个幂式乘积问题，又由于展开式次数较低，所以可以直接展开，然后运用多项式乘法;如果幂指数较大，则分别运用通项公式，再结合多项式乘法.

3)把其中的两项看成一项，连续用通项公式

求底数为三项，并且底数不能分解成两个因式乘积的形式的基本方法:将其中的某两项看成一项(一般都是含有两个未知数，这样将两个未知数分开看成两项)，然后运用二项式展开式展开，按照题目要求，确定相应的常数，再进行讨论.

例8(2015年全国Ⅰ卷理10)(x2＋x＋y)5的展开式中，x5y2的系数为( ).

A.10 B.20 C.30 D.60

解析

(x2＋x＋y)5＝[(x2＋x)＋y]5的通项公式为Tk＋1＝Ck5(x2＋x)5－kyk(k＝0，1，2，…，5)，在展开式中令k＝2，则C25(x2＋x)3＝C25[(x2)3＋3(x2)2x＋3x2x2＋x3]，故x5y2的系数3C25＝30.故选C.

点评

底数既不是完全平方式又不能因式分解，解题时只能把某两项看成一项，到底将哪两项看成一项，要视题设而定，本题把含有x的看成一个整体运算比较方便.

2.2 两项乘积问题

求两个二项式乘积问题的一般方法为，如果两项中一项指数较低(一般为一次或二次)，另一项指数较高，将指数较低的项不动(二次就直接展开)，写出指数较高项的通项公式，运用多项式乘法讨论;若两项的指数都较高，则可以将两项都展开根据多项式乘法讨论，或都写出通项分类讨论.

例9(2019年全国Ⅲ卷理4)(1＋2x2)(1＋x)4的展开式中x3的系数为( ).

A.12 B.16 C.20 D.24

解析

方法1(1＋2x2)(1＋x)4＝(1＋2x2)(1＋4x＋6x2＋4x3＋x4)，所以展开式中x3的系数为1×4＋2×4＝12.故选A.

方法2因为(1＋x)4的通项公式为

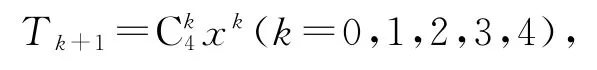
所以展开式中x3的项为

所以x3的系数为12.故选A.

3 会用二项式定理解决整除问题

运用二项式定理解决整除问题在近几年高考中出现的次数很少，但是教材习题中有出现，作为二项式定理的一个知识点，还是有必要掌握这类问题的求解方法，解决这类问题的基本思路是将底数凑成除数的和或差的形式，然后运用二项展开式展开.

例10若是11的倍数，则自然数n为( ).

A.被3除余1的数 B.偶数

C.3的倍数 D.奇数

解析

是11的倍数，所以n＋1为偶数，n为奇数.故选D.

例11若n是正整数，则7n＋7n－1Cn1＋7n－2·Cn2＋…＋7除以9的余数是_________.

解析

因为n是正整数，7n＋7n－1＋…＋＝(7＋1)n－＝8n－1＝(9－1)n－1＝(－1)0＋(－1)1＋…＋·(－1)n－1＋(－1)n－1，则除以9时，若n为偶数，余数为0;若n为奇数，余数为7.

点评

根据这个式子不能直接将底数凑为9，必须分两步完成，将底数中的一个凑为9后展开.

4 应用赋值法解决与二项式有关的问题

在关于二项式定理的运算中，有时要求一些项系数的和或差，解决这类问题的基本方法是直接赋值，有时需要根据式子特征先求导，再赋值.

例12设

解析

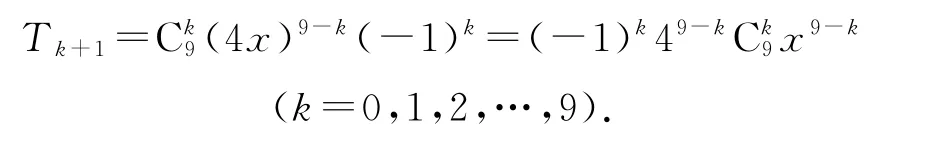
令9－k＝－2，可得k＝11(舍);令9－k＝0，可得k＝9.所以的展开式中的系数为－1，即b＝－1，故

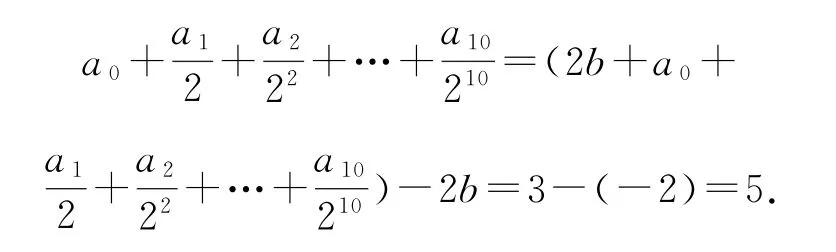
点评

例13若(3－2x)5＝a0＋a1x＋a2x2＋a3x3＋a4x4＋a5x5，则a0＋a1＋2a2＋3a3＋4a4＋5a5的值为_____.

解析

因为

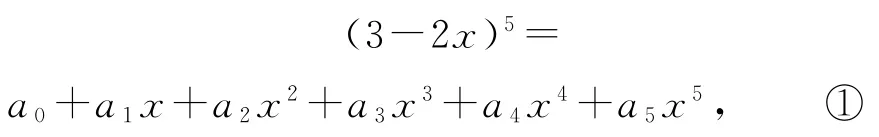
对式①两端求导数，可得

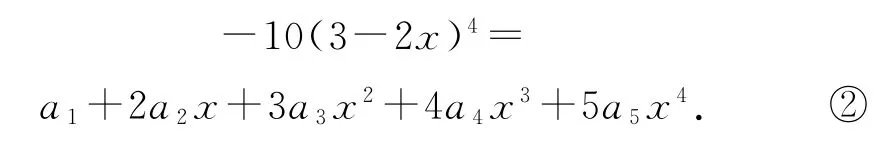
在①中，令x＝0，可得a0＝35;

在②中，令x＝1，可得a1＋2a2＋3a3＋4a4＋5a5＝－10，所以

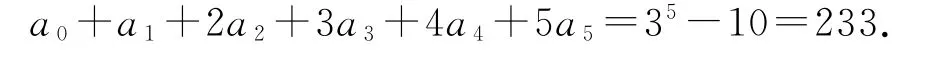
点评

求解这道题时先直接赋值求出a0，再对式子两端求导，最后赋值求出其他剩余的项.

5 关注杨辉三角在数学文化中的应用

解决与杨辉三角有关问题的基本思路:根据杨辉三角每一横行数的特征、斜列数的特征以及每个数与它肩头两个数的关系处理.

例14我国南宋数学家杨辉在所著的《详解九章算法》一书中用如图1所示的三角形解释二项展开式的系数规律，去掉所有为1的项，依次构成2，3，3，4，6，4，5，10，10，5，6，…，则此数列的前50项的和为( ).

图1

A.2025 B.3052 C.3053 D.3049

解析

由图1可知，去除所有为1的项后，前n行共个数，当n＝10时，55，即前10行共有55个数，去除1的项后，第n－1行的和为C1n＋C2n＋…＋Cn－1n＝2n－2，所以前10行的和为212－24＝4072.

点评

解答这道题巧妙地运用了杨辉三角形的性质，即第n行(a＋b)n的展开式的各项的二项式系数依次为

总之，解决二项式定理问题要熟练掌握基本公式，善于发现和总结规律，从而找到解决问题的最佳途径.

链接练习

1.(2021年上海卷春季7)已知(1＋x)n的展开式中，唯有x3的系数最大，则(1＋x)n的系数和为_________.

2.(2021年上海卷夏季6)已知二项式(x＋a)5的展开式中，x2的系数为80，则a＝_________.

3.(2021年浙江卷13)已知多项式(x－1)3＋(x＋1)4＝x4＋a1x3＋a2x2＋a3x＋a4，则a1＝_________；a2＋a3＋a4＝_________.

A.5 B.10 C.15 D.20

链接练习参考答案

1.64.2.2.3.5；10.4.C.