强基计划数学备考系列讲座(1)——组合与概率

王慧兴

(清华大学附属中学)

1 知识技能

2 要点解析

要点1特型方程计数:满足方程x1＋x2＋…＋xn＝m(m，n∈N*)的一个有序整数组(x1，x2，…，xn)，称为该方程的一个整数解.

(1)当m≥n时，方程的正整数解(x1，x2，…，xn)(xi∈N*，1≤i≤n)的个数为;

(2)方程的非负整数解(x1，x2，…，xn)(xi∈N，1≤i≤n)的个数为.

证明(1)任取方程的一个正整数解(x1，x2，…，xn)(xi∈N*，1≤i≤n)，则1≤x1＜x1＋x2＜…＜x1＋x2＋…＋xn－1≤m－1，令x1＋x2＋…＋xi＝yi(1≤i≤m－1)，则有序正整数组(x1，x2，…，xn)与取自集合{1，2，…，n－1}递增正整数组(y1，y2，…，yn－1)一一对应(yn＝m－x1－x2－…－xn－1)，所以方程的正整数解(x1，x2，…，xn)的个数是.

(2)任取一个非负整数解(x1，x2，…，xn)(xi∈N，1≤i≤n)，则x1＋x2＋…＋xn＝m⇔(x1＋1)＋(x2＋1)＋…＋(xn＋1)＝m＋n，令xi＋1＝yi(1≤i≤n)，则原方程的非负整数解(x1，x2，…，xn)与方程y1＋y2＋…＋yn＝m＋n的正整数解(y1，y2，…，yn)一一对应，所以由(1)可知原方程的非负整数解的个数是.

要点2生成函数:无穷项数列{an}的生成函数是指无穷项多项式a1＋a2x＋…＋anxn－1＋…;两个常用生成函数是

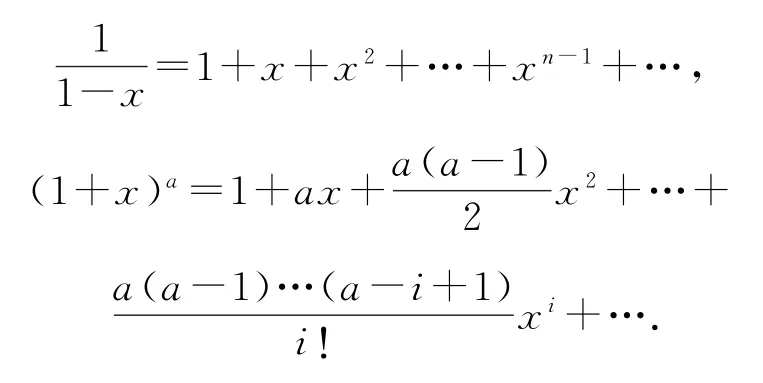
记方程x1＋x2＋…＋xn＝m(m，n∈N*，m＞n)的正整数解(x1，x2，…，xn)个数为am，由

令i＋n＝m，得i＝m－n，故所求方程的正整数解的个数为这就应用生成函数方法再次建立了上述不定方程的正整数解个数.

要点3可重元组合数:给定正整数n，k，则{1，2，…，n}的可重k元组合数是.

证明任取一个这种可重k元组合{x1，x2，…，xk}(用可重元集合表示对应的可重元组合)，不妨设x1≤x2≤…≤xk，则1≤x1＜x2＋1＜…＜xk＋k－1≤n＋k－1，所以可重k元组合{x1，x2，…，xk}与{1，2，…，n＋k－1}的不可重k元组合一一对应，故所求可重k元组合数为

另证记可重k元组合{x1，x2，…，xk}中元素i∈{1，2，…，n}重数是yi，则可重k元组合{x1，x2，…，xk}与有序非负整数组(y1，y2，…，yn)一一对应，故所求k元组合{x1，x2，…，xk}个数等于方程y1＋y2＋…＋yn＝k的非负整数解(y1，y2，…，yn)个数.

要点4映射计数:设A，B是两个非空有限集合，映射f:A→B分类如下.

(1)如果f:A→B是满射，则|A|≥|B|;

(2)如果f:A→B是单射，则|A|≤|B|;

(3)如果f:A→B是双射，则|A|＝|B|(双射转移);

(4)如果满射f:A→B满足B中每个元素恰有k个原象，则|A|＝k|B|.

要点5圆排列:n元圆排列个数是(n－1)!.

证明记n元线排列集合为A，n元圆排列集合为B，把每个线排列中的元素按逆时针顺序依次排在圆周的n个等分点上，则建立了n元线排列与n元圆排列的对应关系，易知映射f:A→B是满射，并且每个圆排列都有n个原象，所以n!＝|A|＝n|B|，故n元圆排列个数是(n－1)!.

要点6置换计数:所谓置换就是指双射f:A→A.建立计数结论，就把集合A界定为有限集(|A|＝n).接下来，我们引入图论方法，构造有向图G(V，E)，其中顶点集V＝A＝{1，2，…，n}，i表示A的元素ai(1≤i≤n)，称为点;边集E＝{(i，j)|f(i)＝j，i，j∈V}，这里本质上E＝{(i，f(i))|i∈V}.由双射迭代，任意的i∈V，存在一个最小正整数ni(1≤ni≤n)，满足fni(i)＝i，因此从i出发，按边的指向，可以得到一个圈i→f(i)→f2(i)→…→fni－1(i)→fni(i)＝i，称为映射圈，同时称最小正整数ni为元素i∈V的阶.这样一个置换f:A→A的图G(V，E)由一些独立(无公共顶点)的映射圈构成，弄清楚图G(V，E)的结构之后，就可以按(双射)f:A→A的已有性质(计数对象双射并没有完全定义)，确定映射圈的个数以及每个映射圈上的点数，据此建立集合A的划分:A＝C1∪C2∪…∪Cr，|Ci|＝ni，圈Ci中的元素的阶都是ni(1≤i≤r≤n)，且n1＋n2＋…＋nr＝n.由于每个圈上的元素结合(象与原象)关系都需要做圆排列，因此圈Ci的个数共有(ni－1)!种，r个确定的圈一起构成一个映射图G(V，E).

注意阶ni的性质:fk(i)＝i(k∈N*)⇒ni|k;取t＝[n1，n2，…，nn]，则ft(i)＝i(任意的i∈A)，即迭代置换ft是恒等置换iA，因此存在最小正整数T，使得fT＝iA，这个正整数T称为置换f:A→A的阶，也有性质:fk＝iA⇒T|k，因此T|t.

为在计算置换f:A→A的个数中考虑重复因素，在此引入“型”的概念，记置换f:A→A含有bi个长为i的圈，称该置换为1b12b23b3…nbn，由此，可以方便地计算置换f:A→A的个数，也就是映射图G(V，E)的个数，即注意，其中应用除法是因为如下两个原因.其一，每个长为k的圈(a1→a2→…→ak→a1)作为一个圆排列，对应于k个不同的线排列，而f:A→A共有bk个不同的长度为k的圈，这bk个圈在n!中引起重复的倍数是kbk;其二，bk个长度为k的不同圈在n!中计入bk!个不同的线排列，再引起重复的倍数bk!.

要点7更列计数:给定正整数n，把1，2，…，n排成一列a1，a2，…，an，满足ai≠i(任意的1≤i≤n)，则称a1，a2，…，an为1，2，…，n的一个更列，记更列数为Mn，则M1＝0，M2＝1，M3＝2，M4＝9，一般地，由递推公式Mn＝(n－1)(Mn－1＋Mn－2)(n≥3)，其通项公式是

读者也可以应用容斥计数原理探究Mn的算法.

要点8分组计数:把n个不同元素分成m组，各组内的元素个数分别记作n1，n2，…，nm.如果元数n1，n2，…，nm互异，则不同分组数是;如果n1＝n2＝…＝nm＝k，则不同分组数是

要点9组合极值:为求一个组合量k的最值，现以最大值kmax为例.

1)一方面，从极端性入手，基于合情思维捕获一个极端例子，得到kmax≥C(常数);另一方面，基于题目结构关系，捕获数据信息，经组合推理，建立kmax≤C，故kmax＝C.

2)从极端性入手，基于合情思维捕获一个k＝C－1的反例，得到kmax≥C;另一方面，再证明该组合量都满足k≤C.故kmax＝C.

要点10点集几何与方法:组合几何中有一项内容就是有限点几何，其中典型问题之一是赫尔伯伦型极值问题，求解策略就是著名的凸包方法——一个有限点集Ω的凸包就是覆盖Ω的最小凸多边形.

要点11条件概率:在事件A发生的条件下事件B发生的概率记为P(B|A)，称为事件A发生条件下事件B发生的条件概率，按定义得

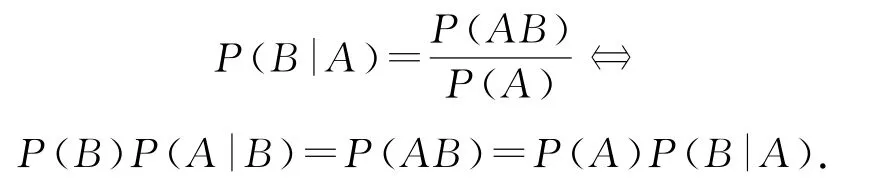
特别地，两个事件A，B互相独立等价于P(B|A)＝P(B)或P(A|B)＝P(A)，即P(AB)＝P(A)P(B);一般地，对n个随机事件A1，A2，…，An，有

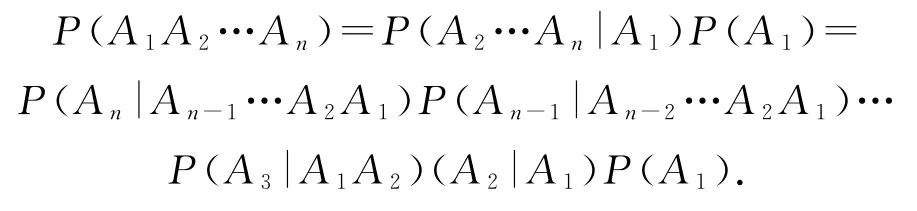
要点12全概率公式与贝叶斯公式:先定义完备事件组的概念，称事件空间Ω的一组事件B1，B2，…，Bn构成一个完备事件组，是指B1∪B2∪…∪Bn＝Ω，且Bi∩Bj＝∅(不可能事件，1≤i＜j≤n).

(1)全概率公式:已知事件空间Ω的一个完备事件组B1，B2，…，Bn，则对任意事件A⊆Ω，都有

(2)贝叶斯(Bayes)公式:条件同上，则

表1中其他知识技能，将在下文例题中渗透，在此不再赘述.

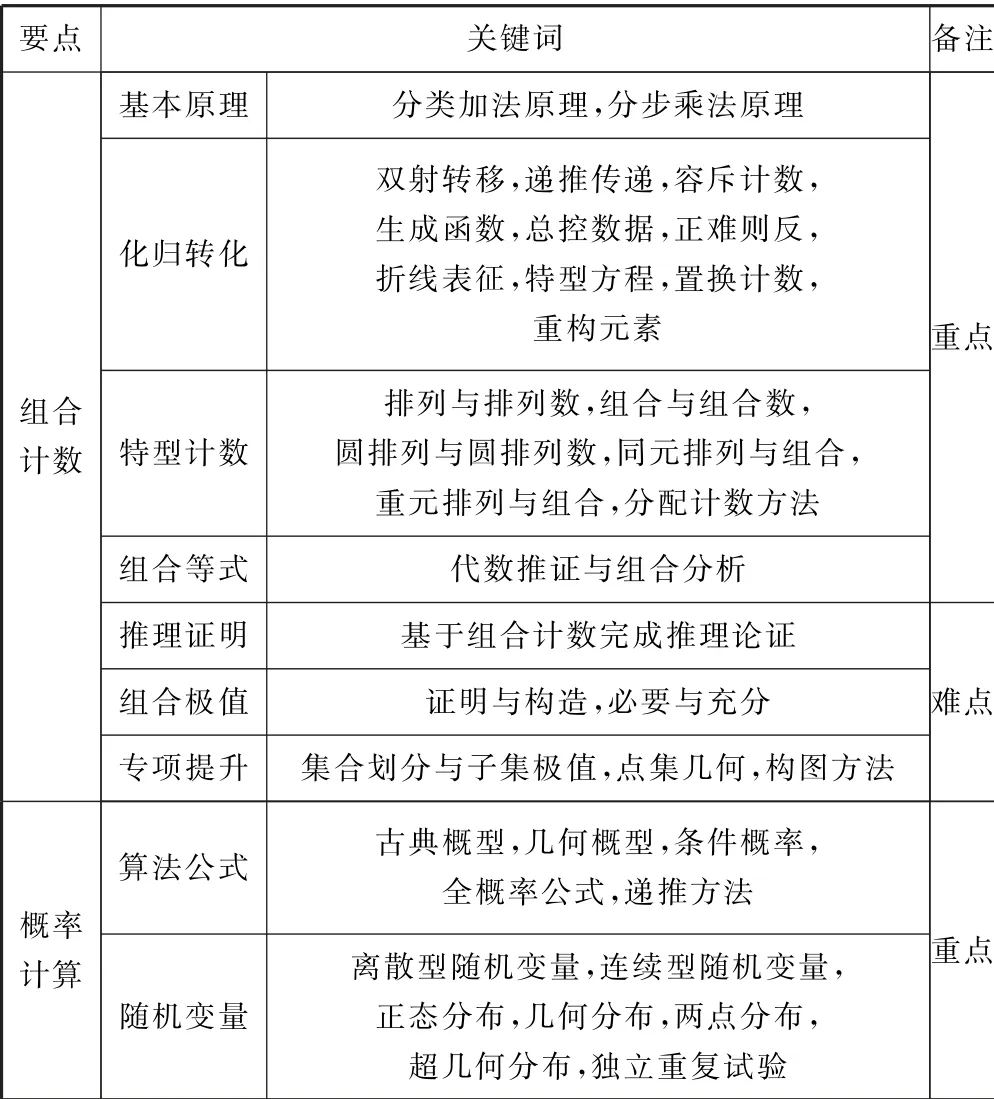
表1

3 典例精析

3.1 组合计数

应用分类加法原理务必严格分类——不重不漏;应用分步乘法原理务必严格分步——不断不叠.强基计划校考中组合计数试题通常兼具分步与分类技能，而且分类复杂，因此，选取一个全集，建立总控数据，基于补集思想，剔除对立面，得到组合计数.除此之外，还有基于转化与化归的双射转移、递推传递、容斥计数、生成函数、折线表征、重构元素等其他策略.

例1(清华大学)满足A∪B⊆C⊆{1，2，…，2020}的子集组(A，B，C)个数是_________.

解析

按题意，子集组(A，B，C)条件等价于A，B⊆C⊆{1，2，…，2020}，按|C|＝i(0≤i≤2020)分类计数，由分步乘法原理，其中满足|C|＝i的子集组(A，B，C)个数是再应用分类加法原理与二项式定理，得满足条件的子集组(A，B，C)个数是

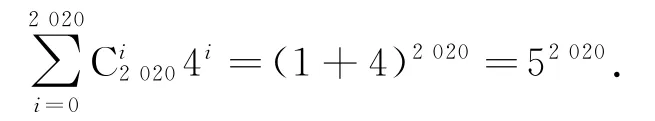
点评

按题意{1，2，…，2020}＝Ω被子集组(A，B，C)划分为五部分，按文氏图(如图1)可应用分步乘法计数原理直接求解.

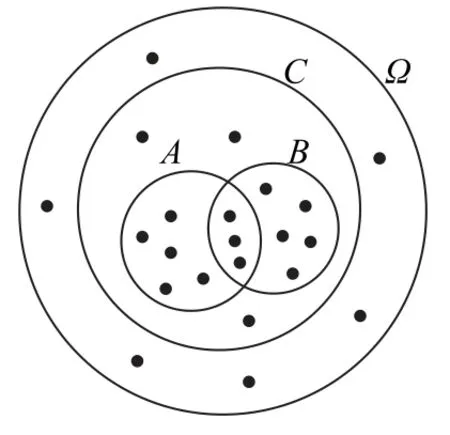
图1

例2(北京大学)要在6×6的方格场地中停放3辆外形完全相同的无牌照红色新轿车与3辆外形完全相同的无牌照黑色新轿车，每一行、每一列都只停放一辆车，每辆车占一格(一个车位)，则所有不同的停放方法种数是_________.

解析

按题意，3辆外形相同的无牌照红色新轿车与3辆外形相同的无牌照黑色新轿车分别视为同元，这为一个“不尽相异元素”的组合计数问题.

点评

也可先选位置再停车.按行分步确定位置共有6!种方法，从选定的6个位置中选出3个位置停放3辆外形相同的无牌照红色新轿车，不同停法是，再把3辆外形相同的无牌照黑色新轿车停放在其余3个不同位置上，只有1种停放方法，所以按分步乘法计数原理，得不同的停放方法数是

例3给定正整数n，集合S＝{1，2，…，10}的所有有序子集组(A1，A2，…，An)构成一个集合T，则

的值是______.

解析

对n＋1元组(A1，A2，…，An，a)(a∈A1∪A2∪…∪An)计数:一方面，对任一有序子集组(A1，A2，…，An)，共有|A1∪A2∪…∪An|个a∈S与之一起构成n＋1元组(A1，A2，…，An，a)，因此，所有n＋1元组(A1，A2，…，An，a)的个数为

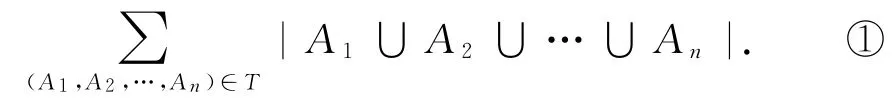
另一方面，对任一a∈S，含这个a的所有有序子集组(A1，A2，…，An)的个数是，因此，所有n＋1元组(A1，A2，…，An，a)的个数为

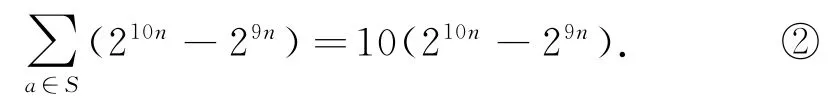
由①和②，得

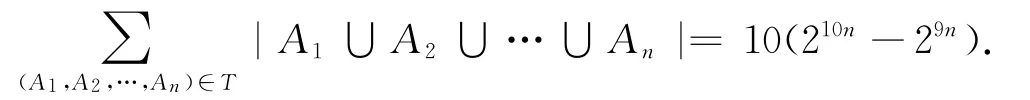
点评

重构元素组是组合计数中的一种常用策略，其根本作用在于存在两种算法视角，通过算两次建构等式，也是避免重复计数的一种策略.

例4方程x＋y＋z＝2022的满足x≥y≥z的正整数解(x，y，z)个数是________.

解析

以方程x＋y＋z＝2022的所有正整数解数作为总控数据，再分析其中数据结构，剔除对立数据.

记Ω＝{(x，y，z)|x＋y＋z＝2022，x，y，z∈，其中

由B1＝{(a，a，2b′)|a＋b′＝1011，a，b′∈N*，a≠2b′}，得|B1|＝1009.

同理，|B2|＝1009＝|B3|，故|A2|＝1009×3.

记C＝{(x，y，z)∈Ω|x＞y＞z，x，y，z∈N*}，则A3＝3!·|C|.

因为|A1|＋|A2|＋|A3|＝，所以

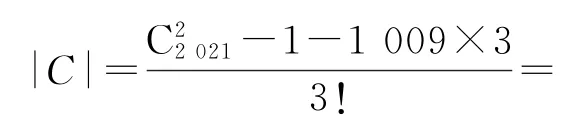
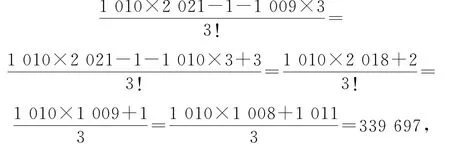
故所求正整数解数为

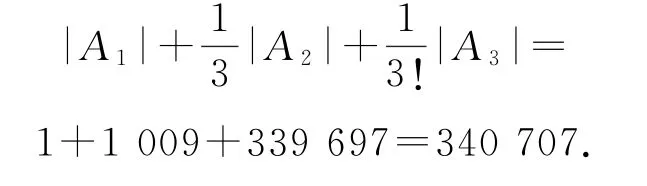
3.2 概率计算

除针对基本概型(古典概型、几何概型、条件概率)计算概率之外，在统计与分布等问题中也有概率计算.

例5一项“过关游戏”规则规定:在第n关要抛掷一颗骰子n次，如果这n次抛掷所出现的点数之和大于2n，则算过关.问:

(1)某人在这项游戏中最多能过几关?

(2)求他连过前三关的概率.

注:骰子是一个在6个面上分别标有1，2，3，4，5，6点数的质地均匀正方体，抛掷骰子落地静止后，向上一面的点数为出现的点数.

解析

(1)按题意，此人能过第n关的条件是他连续抛掷n次骰子，出现的点数之和应大于2n，所以过第n关的必要条件是6n＞2n，从而n≤4，故此人至多能过第4关.

(2)记过第n关的概率为Pn(n＝1，2，3)，则此人连过3关的概率P＝P1P2P3，下面分别计算P1，P2，P3.

过第一关的条件是抛掷一次骰子出现的点数大于2，即出现的点数可以是3，4，5，6，所以

过第二关的条件是连续两次抛掷骰子出现的点数之和大于4，记连续两次抛掷骰子出现的点数分别为x1，x2，则P2＝P(x1＋x2＞4)＝1－P(x1＋x2≤

过第三关的条件是连续三次抛掷骰子出现的点数之和大于8，记连续三次抛掷骰子出现的点数分别为x1，x2，x3，则

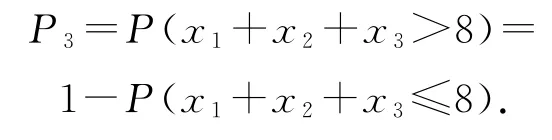
因为不定方程x1＋x2＋x3＝k的正整数解个数是(3≤k≤8)，所以满足x1＋x2＋x3≤8的有序正整数组(x1，x2，x3)个数是故

点评

第(2)问直接求满足x1＋x2＋x3＞8，即x1＋x2＋x3＝k(k＝9，10，11，…，18)是难点，因为每个变量带有条件1≤xi≤6，所以按公式得到的不定方程的解数有不可能发生的正整数组(x1，x2，x3).因此，本题解法坚持正难则反，化难为易原则.

例6两个相同的正四面体，四个面分别标有1，2，3，4，某人每次同时投掷这两个正四面体，规定每次两底面上数字之和为所得数字，共投掷三次，则三次所得数字之积能被10整除的概率是( ).

解析

每次投掷所得数字X是一个随机变量，X的概率分布如表2所示.

表2

记三次投掷所得数字分别为X，Y，Z，则

10|XYZ⇔X，Y，Z中 必有5与偶数.

若X，Y，Z恰有1个5，则另两个必有偶数，这包括另两个都是偶数或一个是偶数，另一个是不为5的奇数，概率为

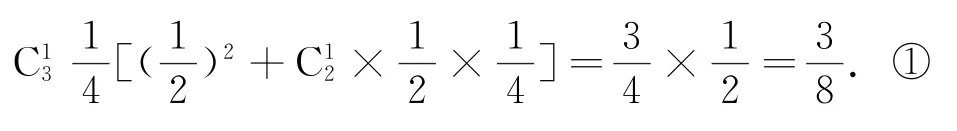
若X，Y，Z恰有2个5，则另一个必为偶数，概率为

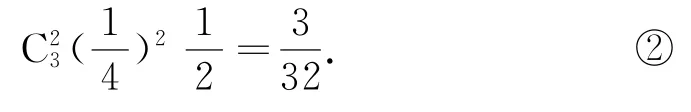
另解直接用概率计算

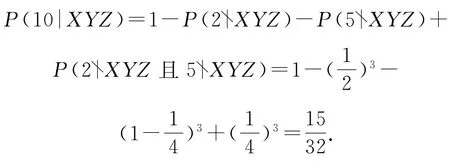
例7(清华大学)抛掷n次硬币，记不连续出现三次正面朝上的概率为Pn.

(1)求P1，P2，P3，P4;

(2)求{Pn}的递推公式;

解析

(2)当n≥4时，按第n次反面朝上与正面朝上分成两类.

当第n次反面朝上，形如“…反”，这种结果中不出现连续三次正面朝上的概率等于Pn－1，但第n次出现反面朝上的概率是，按积事件的概率公式，可得当第n次反面朝上时不出现连续三次正面朝上的概率是

当第n次出现正面朝上，这种事件是两种互斥事件“…反正”与“…反正正”的和事件，其概率是

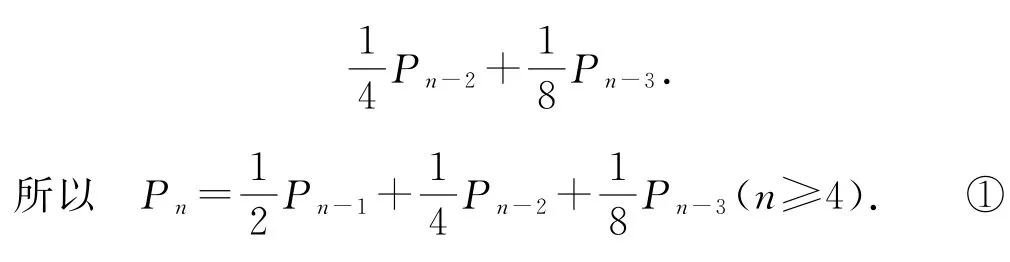
(3)先证数列{Pn}存在极限，为此，我们证明该数列单调有界:由于0＜Pn＜1，任意的n∈N*，只需证明该数列单调递减.

由①－②，可得，当n≥5时，恒有Pn＝Pn－1－.任意的n∈N*，所以存在，记

点评

本题是数列、递推与极限的典型应用题，上述解法基于数列单调有界必有极限，通过解方程求出极限，方法通用、快捷.

例8有朋友自远方来访，乘火车来的概率为乘船、乘汽车、乘飞机来的概率分别是已知他乘火车来迟到的概率是乘船来迟到的概率为乘汽车来迟到的概率为如果他乘飞机来就不会迟到(迟到的概率是0).在结果是迟到的情形下，求他乘火车的概率.

解析

以B表示事件“迟到”;用A1，A2，A3，A4分别表示事件:“乘火车”“乘船”“乘汽车”“乘飞机”，由Bayes公式，得

3.3 推理与证明

例9求证集合S＝{1，2，3，…，24}的任一17元子集T中都有3个元素两两互素.

证明作二划分S＝B∪C，B＝{4，6，8，9，10，12，14，15，16，18，20，21，22，24}，C＝{1，2，3，5，7，11，13，17，19，23}，其 中C中 任 意3个 数 都 是 两 两 互素的.

任取17元子集A⊂S，由7＝|A|＝|S∩A|＝|A∩B|＋|A∩C|≤14＋|A∩C|，得|A∩C|≥3，所以A中至少有3个数两两互素，由A的任意性，命题得证.

例10把－1，1以任意方式填入一个n×n(n≥4)方格表，把位于不同行不同列的n个数之积称作一个基本量，记所有基本量之和为S，求证:S是4的倍数.

证明记第i行第j列小方格填入的数为ai，j∈{－1，1}(1≤i，j≤n)，则 基 本 量 通 式 为a1，i1a2，i2a3，i3…an，in∈{－1，1}.记所有基本量中取值为－1的个数为k，则取值为1的基本量个数为n!－k.

一方面，所有基本量之和为

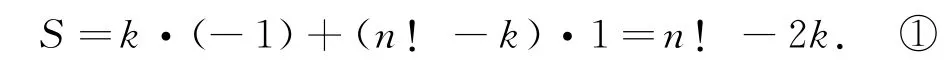
另一方面，计算所有基本量之积，得

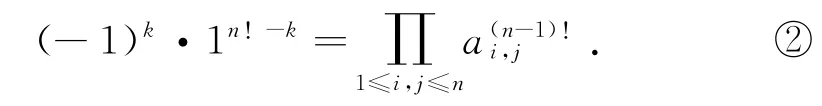
因为整数n≥4，所以2|(n－1)!，所以由②得

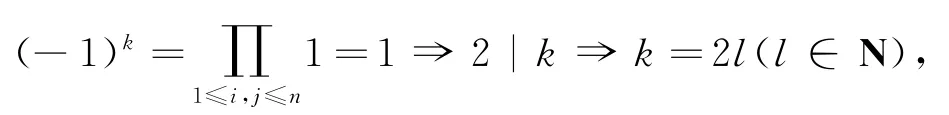
代入①，得S＝n!－4l≡0(mod4).

3.4 最值与构造

例11集合S＝{1，2，3，4，5}的一组子集A1，A2，…，Ak，其中任意两个子集都没有包含关系，求kmax.

解析

一方面，取出S的C25＝10个2元子集，得到一个满足题意的子集组，所以

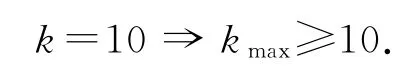
另一方面，把S的全部25＝32个子集如下分成10组，每一组都是一个“包含链”:

所以，上述每一条子集链上至多取出1个子集，组成符合题意的子集组，从而k≤10，即kmax≤10.

综上，得kmax＝10.

一般地，n元集合S＝{1，2，…，n}的一组子集A1，A2，…，Ak，两两互不包含，即Ai⊈Aj且Ai⊉Aj(任意的1≤i＜j≤n)，则

事实上，一方面，把每个Ai的元素进行全排列，得到|Ai|!个|Ai|元排列，再把其补集的全部元素进行全排列，得到(n－|Ai|)!个n－|Ai|元排列，前后对接得到|Ai|!·(n－|Ai|)!个n元排列;由组子集A1，A2，…，Ak中任意两个子集互不包含，则对任意两个不同子集，上面构建的不同组的n元排列都没有重复，所以

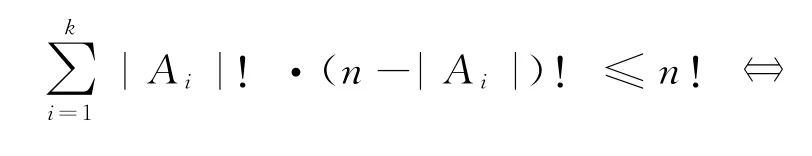
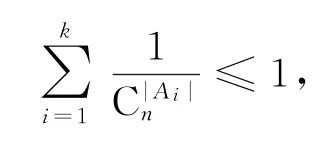
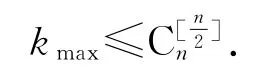
另一方面，取出集合S的全部元子集构成一个符合题意的子集组，此时从 而kmax≥

例12集合S＝{1，2，3，…，n}的一组非空子集A1，A2，…，Ak，其中任意两个要么有包含关系，要么两者交集是空集，求kmax.

解析

一方面，集合S的子集组{1}，{1，2}，{1，2，3}，…，{1，2，…，n}，{2}，{3}，{4}，…，{n}满足题意，此时k＝2n－1，因此kmax≤2n－1.

另一方面，下证kmax≥2n－1，即证k≤2n－1.

首先，当n＝1时，S＝{1}符合题意的非空子集组只有1个子集，从而k≤1;当n＝2时，S＝{1，2}符合题意的非空子集组，子集个数最多的是{1}，{2}，{1，2}，因此k≤3.

假设对n≤l，都有k≤2n－1，下证当n＝l＋1时，也有k≤2n－1.

任取S＝{1，2，…，l，l＋1}的符合题意的子集组A1，A2，…，Ak，除其中可能有{1，2，…，l，l＋1}之外，取出其余k－1个子集中元素最多的一个子集E，则|E|≤l.再把这k－1个子集都与E比较，分成两类.

第一类:Ai1，Ai2，…，Aix⊆E，其中任意两个有包含关系或不相交，由归纳假设，可知x≤2|E|－1.

第二类:Aj1，Aj2，…，Ajy，都与E交集为空集，则这些子集都是∁SE的子集，且其中任意两个有包含关系或交集为空集，从而由归纳假设，得

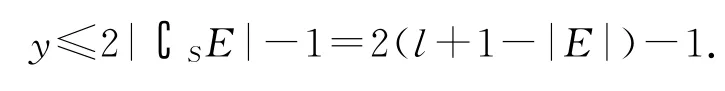
故

由数学归纳法，k≤2n－1得证.

综上，kmax＝2n－1.

例13(北京大学)在(2019×2020)2019的全体正因数中选若干个，使得其中任意两个的乘积都不是平方数，则最多可选因数个数为( ).

A.16 B.31

C.32 D.前三个答案都不对

解析

记符合条件的因子组为A(视为集合)，下证|A|max＝32.作素因子分解

记

一方面，取b的全部正约数构成因子组B，即B＝{t∈N*|t|b}，则B是正整数a的符合题意的因子组，并且|B|＝25＝32，从而

另一方面，对正整数a的任一因子组A.

情形一:A⊆B，则|A|≤|B|＝32.

情形二:A⊄B，即存在2u3v5w101z673y∈A(u，v，w，z，y∈N)，但2u3v5w101z673y∉B，亦 即max{u，v，w，z，y}＞1，不妨设u＞1，作带余除法u＝2k＋r(k∈N*，r∈{0，1})，由

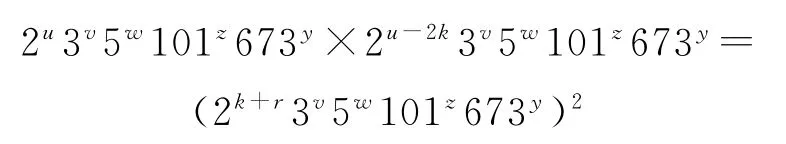
是一个完全平方数，所以2u－2k3v5w101z673y∉A.再由u－2k与u奇偶性相同，以2u－2k3v5w101z673y替换A中的2u3v5w101z673y得到a的符合条件的另一因子组A1，并且|A1|＝|A|.

如果A1中仍然存在一个数，它不是正整数b的约数，再做一次上述替换，得到符合条件的另一因子组A2，并且|A2|＝|A1|.

经有限次上述替换操作，得到一些列符合条件的a因子组A1，A2，…，Al(l∈N*)，满足

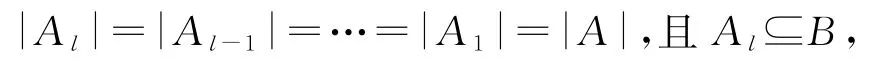
所以|A|≤|B|＝32.

综上，|A|≤32，由A的任意性，可得

由①和②，得|A|max＝32.

4 实战演练

1.给定正整数n，正整数a，b，c为一个三角形的三条边长，且b≤n，a≤b≤c，则这种三角形个数是_________.

2.(上海交大)任意投掷3枚骰子，则三个面朝上的点数恰好组成等差数列的概率为________.

3.设集合A＝{1，2，3，…，10}，映射f:A→A满足下列两条件:(1)f30(x)＝x(任意的x∈A);(2)对满足1≤k≤29的每个整数k，至少存在一个a∈A，使得fk(a)≠a，求这种映射的个数.

4.1，2，3，4，5的 排 列a1，a2，a3，a4，a5满 足:对1≤i≤4，a1，a2，…，ai不构成1，2，…，i的某个排列，求这种排列a1，a2，a3，a4，a5的个数.

5.甲、乙等4人互相传球，第一次由甲先把球传出，每次传球时，传球者将球等可能地传给另外3人之一.

(1)经过2次传球后，球在甲乙两人手中的概率各是多少?

(2)经过n次传递之后，球在甲手中的概率记为Pn(n＝1，2，…)，求Pn与{Pn}的极限.

6.某人忘记了电话号码的最后一个数字，因此他随意拨号，求他拨号不超过3次而接通的概率.

7.某电子设备制造厂所用元件是由三家元件制造厂提供的，过往记录数据如表3所示.

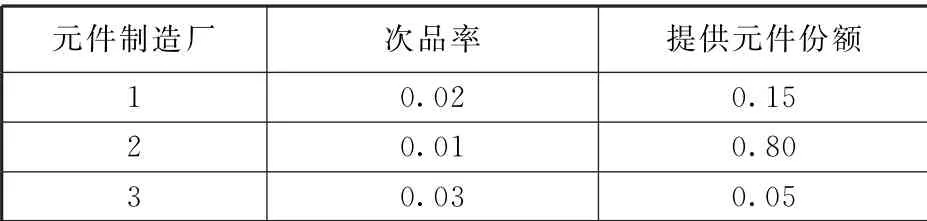
表3

设这三家工厂的产品在仓库中是均匀混合的，并且无区别标志.

(1)在仓库中随机取出一只元件，求它是次品的概率;

(2)在仓库中随机取出一只元件，若已知取到的是次品，为分析此次品来自何厂，需求出此次品由三家工厂生产的概率分布是多少.

8.盒中放有12个乒乓球，其中9个是新的，第1次比赛时从中取出3个来用，比赛后放回盒中，第2次比赛时再从盒中取出3个(精确到0.001).

(1)求第2次取出的球都是新球的概率;

(2)已知第2次取出的球都是新球，求第1次取到的3球都是新球的概率.

图2

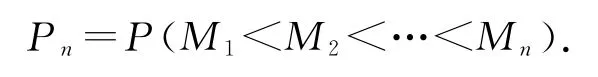
10.(复旦大学)有2个细胞，每个细胞每次分裂成2个细胞或死亡的概率均为求分裂2次后，有细胞成活的概率P.

11.某个系统中每个元件正常工作的概率是p(0＜p＜1)，各个元件是否正常工作相互独立;如果系统中有多于一半的元件正常工作，系统就能正常工作;系统正常工作的概率称为系统的可靠性.

(1)该系统配置有2k－1(k∈N*)个元件，求该系统正常工作概率的表达式;

(2)现为改进系统性能，拟增加两个元件，试讨论增加两个元件后，能够提高系统的可靠性.

12.已知平面上n个点，其中任何3点都是直角三角形的3个顶点，求nmax.

13.在n边形内分布k个点，使得在以该n边形的任意3个顶点为顶点的三角形内都至少有1个点，求kmin.

14.在m×n的矩形方格纸上画一条直线，记这条直线与k个小方格相交(矩形内含有直线上一段)，求kmax.

15.将一个正方体剖分成互不重叠的k个四面体，求kmax.

16.某公司需要录用一名秘书，共有10人报名，公司经理决定按照求职报名的顺序逐个面试，前3名面试后一定不录用，自第4个人开始将他与前面面试过的人相比较，如果他的能力超过了前面所有已面试过的人，就录用他，否则就不录用，继续面试下一个.如果前9个人都不录用，那么就录用最后一个面试的人.

假定这10个人的能力各不相同，可以按能力由强到弱排为第1，第2，…，第10，显然该公司到底录用哪一个人，与这10个人报名顺序有关.大家知道，这样的排列共有10!种，以Ak表示能力第k的人被录用的不同报名顺序数目，以表示他被录用的可能性.

证明:在该公司经理的方针之下，有

(1)A1＞A2＞…＞A8＝A9＝A10;

(2)该公司有超过70%的可能性录用到能力最强的3个人之一，而只有不超过10%的可能性录用到能力最弱的3个人之一.