算盘巧入题，情境妙设置

韩计峰

(山东省邹城市实验中学)

算盘是一种手动操作进行计算的辅助工具.它起源于中国，是在长期使用算筹的基础上发明的，迄今已有2600多年的历史，是中国古代一项伟大、重要的发明，在阿拉伯数字出现前是全世界广为使用的计算工具.“珠算”一词最早见于东汉徐岳所撰的《数术记遗》，其中有云:“珠算控带四时，经纬三才.”北周甄鸾为此作注，大意是把木板刻为3部分，上、下两部分是停游珠用的，中间一部分是作定位用的.借助算盘巧妙入题，创设创新情境与文化氛围，合理融入计数原理、排列与组合、概率与统计等相关知识，是新高考数学试卷中比较常见的一类数学文化试题.

1 计数问题

例1算盘是中国古代的一项重要发明.现有一种算盘(如图1-甲)，共两档，自右向左分别表示个位和十位，档中横以梁，梁上一珠拨下，记作数字5，梁下五珠，上拨一珠记作数字1(图1-乙中算盘表示整数51).如果拨动图1-甲算盘中的三枚算珠，可以表示不同整数的个数为( ).

图1

A.16 B.15 C.12 D.10

分析分如下四种情况进行分类讨论:①个位拨动三枚;②十位拨动一枚，个位拨动两枚;③十位拨动两枚，个位拨动一枚;④十位拨动三枚.进而分别列举出每种情况下对应的数字，利用分类加法计数原理可得出结果.

解由题意，拨动三枚算珠，有4种不同的拨法.

①个位拨动三枚，有2种结果:3，7;

②十位拨动一枚，个位拨动两枚，有4种结果:12，16，52，56;

③十位拨动两枚，个位拨动一枚，有4种结果:21，25，61，65;

④十位拨动三枚，有2种结果:30，70.

综上，拨动题图1-甲算盘中的三枚算珠，可以表示不同整数的个数为2＋4＋4＋2＝12，故选C.

点评

破解本题的关键是根据算盘中个位、十位不同的拨动情况进行合理分类讨论.针对算盘中梁上与梁下算珠的不同表达方式，合理分类讨论，分类时要做到不重不漏.

2 排列组合问题

例2图2是一把算盘的初始状态，自右向左，分别是个位、十位、百位、…，上面一粒珠(简称上珠)代表5，下面一粒珠(简称下珠)代表1，即五粒下珠的大小等于同组一粒上珠的大小.现在从个位、十位和百位这三组中随机选择往下拨1粒上珠，且往上拨2粒下珠，则算盘表示的数的个数为( ).

图2

A.9 B.18 C.27 D.36

分析通过算盘上珠与下珠的不同操作情况进行分步处理，在不同珠的处理过程中进行组合计数分析，结合分步计数原理确定算盘表示的数的个数.

解根据珠算的运算法则以及题干中描述的操作，从个位、十位、百位上珠中选1粒往下拨，则可表示C13个数.

下珠往上拨分两种情况，全部来自个位或十位或百位，即可表示C13个数，或者来自个位、十位、百位中的两个，即可表示C23个数.

综上，算盘表示的数的个数为C13(C13＋C23)＝18，故选B.

点评

本题主要考查组合计数以及分步计数原理的应用.借助排列组合以及计数原理来确定算盘中表示数的个数问题，要对算盘各数位、上珠与下珠情况以及不同情况进行合理分析，综合考查逻辑推理、代数运算等核心素养.

3 概率问题

例3 算盘是中国传统的计算工具，其形长方，周为木框，内贯直柱，俗称“档”，档中横以梁，梁上两珠，每珠作数五，梁下五珠，每珠作数一.算珠梁上部分叫上珠，梁下部分叫下珠.如图3所示，在十位档拨上一颗上珠和两颗下珠，个位档拨上四颗下珠，则表示数字74.若在个位、十位、百位、千位档中随机选择一档拨上一颗下珠，再随机选择两个不同档位各拨一颗上珠，则所表示的数字大于300的概率为________.

图3

分析先分析所有表示的数的种数，然后考虑所表示的数不大于300的种数，即下珠在个位、十位档上;下珠在百位档上.通过对立事件的概率，采用“正难则反”思想进行分析与求解.

解由题意，在个位、十位、百位、千位档中随机选择一档拨上一颗下珠，再随机选择两个不同档位各拨一颗上珠，共有C14C24＝24种.

在个位、十位档中随机选择一档拨上一颗下珠，再随机从个位、十位两个不同档位各拨一颗上珠时，得到的数字不大于300，共有C12C22＝2种.

在百位档中随机选择一档拨上一颗下珠，再随机从个位、十位两个不同档位各拨一颗上珠时，得到的数字不大于300，有C22＝1种.

综上，所拨数字大于300的概率为

点评

解答本题的关键在于理解每个档位上的算珠所表示的数字大小以及“正难则反”思想的运用.破解此类创新概率问题往往要结合古典概型或几何概型，利用排列组合等相关知识，综合一些常见的数学思维，结合对立事件、互斥事件以及条件概率等合理求解.

4 综合问题

例4(多选题)算盘是我国古代一项伟大的发明，是一种重要的计算工具.图4是一把算盘的初始状态，自右向左，分别表示个位、十位、百位、千位、…，上面一粒珠子(简称上珠)代表5，下面一粒珠子(简称下珠)代表1，五粒下珠的大小等于同组一粒上珠的大小.例如，个位拨动一粒上珠、十位拨动一粒下珠，表示数字15.现将算盘的个位、十位、百位、千位分别随机拨动一粒珠子，设事件A:“表示的四位数能被3整除”，事件B:“表示的四位数能被5整除”，则( ).

图4

分析只拨动一粒珠子，因此数字只表示1或5，由此可得四位数的个数.而能被3整除，只能是2个1和2个5，求出四位数的个数后可得概率.而被5整除，只要个位数字是5即可.由此计数后可计算出概率，判断各选项.

解现将算盘的个位、十位、百位、千位分别随机拨动一粒珠子，基本事件总数为24＝16，事件A包含的四位数有1155，1515，1551，5511，5115，5151，共6个，则故A正确.

事件B包含的基本事件有1115，1155，1515，1555，5555，5115，5155，5515，共8个，则P(B)＝故B错误.

事件A∪B包含的基本事件有:1155，1515，1551，5511，5115，5151，1115，1555，5555，5155，5515，共11个，则故C正确.

事件AB包含的基本事件有1155，1515，5115，共3个，则故D正确.

综上，选ACD.

点评

本题主要以古典概型为问题背景，结合算盘创新情境合理设置多选题，涉及互斥事件、独立事件等概率知识.解题时合理计数，正确剖析，借助对应的概率公式以及思想方法处理，巧妙判断.

5 变式练习

1.珠算是以算盘为工具进行数字计算的一种方法，2013年年底联合国教科文组织将中国珠算项目列入人类非物质文化遗产名录.算盘的每个档(挂珠的杆)上有7颗算珠，用梁隔开，梁上面的两颗珠叫“上珠”，下面的5颗叫“下珠”，从最右边两档的14颗算珠中任取1颗，则这一颗是上珠的概率为( ).

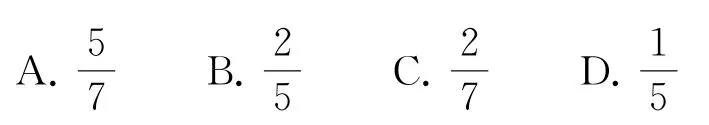
解析

从最右边两档的14颗算珠中任取1颗，基本事件总数为14，这一颗是上珠包含的基本事件个数为4，所以这一颗是上珠的概率为故选C.

2.我国古代算盘每个档(挂珠的杆)上有7颗算珠，用梁隔开，梁上面两颗叫上珠，上珠每颗代表数值5，下面5颗叫下珠，下珠每颗代表数值1，现从某一档的7颗算珠中任取4颗(这4颗算珠最小表示数值4，最大表示数值12)，则所取的算珠表示的数值是8的概率为( ).

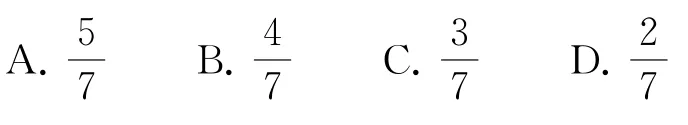
解析

从某一档的7颗算珠中任取4颗，基本事件总数为C47＝35，所取的算珠表示的数值是8包含的基本事件个数为C12C35＝20，则所取的算珠表示的数值是8的概率为故选B.

3.算盘每个档(挂珠的杆)上有7颗算珠，用梁隔开，梁上面两颗叫上珠，下面5颗叫下珠.若从某一档的7颗算珠中任取3颗，至少含有一颗上珠的概率为( ).

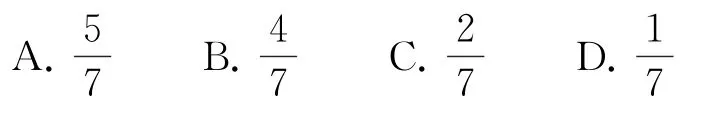
解析

从某一档的7颗算珠中任取3颗，基本事件总数为C37＝35，至少含有一颗上珠包含的基本事件个数为C22C15＋C12C25＝25，所以至少含有一颗上珠的概率为故选A.

借助算盘这一基本计数与运算工具，合理创新问题情境，问题往往综合融入计数原理、排列组合、概率与统计等相关数学基础知识，综合考查计数、排列组合、概率、统计以及综合应用.