基于数学思想引领与素养导向的“概率与统计”复习

巨小鹏

(陕西省汉中市龙岗学校)

自《普通高中数学新课程标准(2017版2020年修订)》(以下简称:新课标)实施以来，对概率与统计这一部分内容的考查变化很大，增删调整了很多内容，这也标志着对概率与统计这一部分内容的要求更加完善和明确.数学教学中的深度学习就是学生以主动积极的情感，将思维特别是高阶思维贯穿到数学学习过程的始终，他们不仅要关注知识技能“是什么”“怎样用”，还要探究知识技能的来龙去脉.数学思想就是从高阶思维角度阐述数学知识的规律和思维逻辑的本质，将数学复习提升到思想方法的层面，以达到深度复习的效果.

1 精准领会新课标要求

1.1 新、旧课标区别分析

对于概率这一部分内容，新课标增加了“理解样本点和有限样本空间的含义”“理解概率的性质，掌握随机事件的运算法则”，强调“了解随机事件的并、交与互斥的含义，能结合实例进行随机事件的并、交计算”，增加了“结合有限样本空间，了解两个随机事件独立性的含义，结合古典概型，利用独立性计算概率”.

对于统计这一部分内容，新课标增加了“普查和抽查、互联网获取数据的途径”“了解总体、样本、样本量的概念，了解数据的随机性”“会计算样本均值和样本方差，了解样本与总体的关系”，新课标对分层抽样提出更加细致的要求，要求掌握各层样本量比例分配的方法和分层随机抽样的样本均值和样本方差，比旧课标提高了要求.新课标删除了系统抽样的方法，增加了“能根据实际问题的特点，设计恰当的抽样方法解决问题”，进一步凸显数学知识在解决问题中的作用.新课标强调“能根据实际问题的特点，选择恰当的统计图表”，强调了平均数、中位数、众数均体现数据的集中趋势，提高了对众数和中位数的要求，并要求学生理解集中趋势参数的统计含义，强调了标准差、方差和极差体现数据离散趋势，提高了对方差和极差的要求，并要求学生理解离散程度参数的统计含义，删除了对“初步体会样本频率分布和数字特征的随机性”的要求，删除了对“形成对数据处理过程进行初步评价的意识”的要求，增加了对“能用样本估计百分位数，理解百分位的统计含义”，对样本数据的分析提出了新的要求.

1.2 七了解、八理解、三会和五掌握

七了解:随机事件的并、交与互斥的含义;两个随机事件独立的含义;总体、样本、样本量的概念;数据的随机性;简单随机抽样的含义及其解决问题的过程;样本与总体的关系;分层随机抽样的特点和适用范围，分层随机抽样的必要性.

八理解:古典概型;概率的性质;集中趋势参数的统计含义;离散程度参数的统计含义;百分位数的统计含义;样本点、有限样本空间、随机事件;样本点和有限样本空间的含义;随机事件与样本点的关系.

三会:用频率估计概率;计算样本均值和样本方差;计算古典概型中简单随机事件的概率.

五掌握:分层随机抽样的样本均值和样本方差;随机事件概率的运算法则;抽签法;随机数法;各层样本量比例分配的方法.

重点提升数据分析、数学建模、逻辑推理和数学运算素养.

2 数学思想方法引领下的复习

2.1 数形结合，厘清基本概念

借助树状图、表格或者坐标系等工具进行直观表达，厘清基本概念和基本问题，有利于分析、解决问题.

例1(北师大版《必修3》)小明家的晚报在下午5:30～6:30之间的任何一个时间随机地被送到，小明一家人在下午6:00～7:00之间的任何一个时间随机地开始晚餐，那么晚报在晚餐开始之前被送到的概率是多少?

解析

设晚报被送到的时间为x时，晚餐开始的时间为y时，则

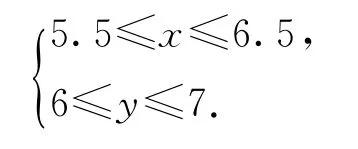
如图1所示，表示区域是边长为1的正方形，面积S＝1;事件:“晚报在晚餐之前被送到”即为x≤y，设事件A:“晚报在晚餐之前被送到”，表示区域为阴影部分，面积

图1

点评

解答本题的关键是能通过所给的条件准确作出可行域.在利用几何概型的概率公式求概率时，几何“测度”可以是长度、面积、体积、角度等，其中几何度量为长度、面积、体积时的等可能性主要体现在点落在区域Ω上的任何位置都是等可能的.

2.2 分类讨论，凸显概率模型

例2(2021年全国甲卷理10)将4个1和2个0随机排成一行，则2个0不相邻的概率为( ).

解析

方法1将4个1和2个0随机排成一行，可利用插空法，4个1产生5个空，若2个0相邻，有＝5种排法，若2个0不相邻，有＝10种排法，故2个0不相邻的概率为故选C.

方法24个1和2个0随机排成一行，共有种排法.2个0不相邻，先将4个1全排列，再用插空法将2个0放入，共有＝10种排法，故2个0不相邻的概率为.故选C.点评

计数原理问题能体现分类讨论的思想，随机事件中样本点的计算和随机变量取值下的概率计算也会用到分类讨论.

2.3 函数与方程，强化基础

例3(2017年全国Ⅱ卷理13)一批产品的二等品率为0.02，从这批产品中每次随机取一件，有放回地抽取100次，X表示抽到的二等品件数，则D(X)＝_________.

解析

由于是有放回的抽样，所以X服从二项分布，即X～B(100，0.02)，则

点评

本题考查离散型随机变量方差的求法、二项分布的性质等基础知识，考查运算求解能力、函数与方程思想，比较基础.

2.4 化归转化，以旧攻新

例4(2017年全国Ⅰ卷文19)为了监控某种零件的一条生产线的生产过程，检验员每隔30 min从该生产线上随机抽取一个零件，并测量其尺寸(单位:cm).表1是检验员在一天内依次抽取的16个零件的尺寸.

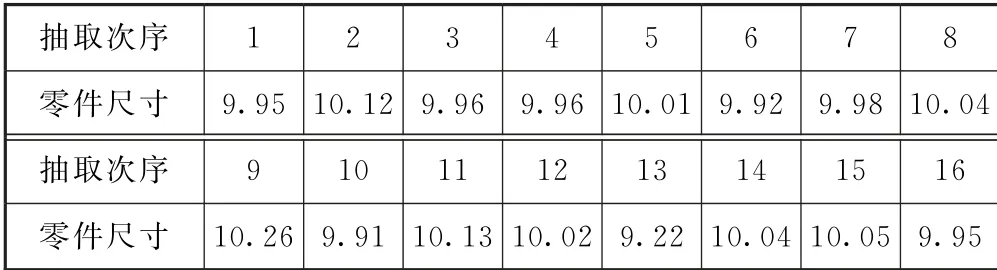
表1

其中xi为抽取的第i个零件的尺寸，i＝1，2，…，16.

(1)求(xi，i)(i＝1，2，…，16)的相关系数r，并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若|r|＜0.25，则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).

(ⅰ)从这一天抽检的结果看，是否需对当天的生产过程进行检查?

附:样本(xi，yi)(i＝1，2，…，n)的相关系数

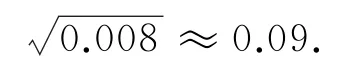
解析

(1)(xi，i)(i＝1，2，…，16)的相关系数为r＝

因为|r|＜0.25，因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.

(2)(ⅰ)由于¯x＝9.97，s≈0.212，由样本数据可以看出抽取的第13个零件的尺寸在(¯x－3s，¯x＋3s)以外，因此需对当天的生产过程进行检查.

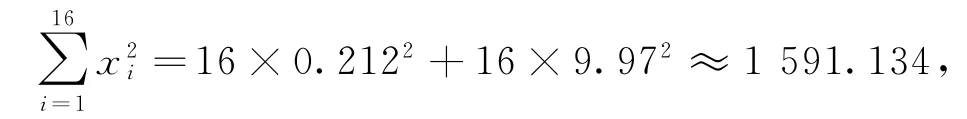
剔除第13个数据，剩下数据的样本方差为

这条生产线当天生产的零件尺寸的标准差的估计值为0.09.

点评

解答创新题时，一要通过转化，化“新”为“旧”;二要通过深入分析，多方联想，以“旧”攻“新”;三要创造性地运用数学思想方法，以“新”克“新”，应特别关注创新题型的切入点.

2.5 函数思想，攻坚克难

例5(2021年新高考Ⅱ卷21)一种微生物群体可以经过自身繁殖不断生存下来，设一个这种微生物为第0代，经过一次繁殖后为第1代，再经过一次繁殖后为第2代……该微生物每代繁殖的个数是相互独立的且有相同的分布列，设X表示1个微生物个体繁殖下一代的个数，P(X＝i)＝pi(i＝0，1，2，3).

(1)已知p0＝0.4，p1＝0.3，p2＝0.2，p3＝0.1，求E(X);

(2)设p表示该种微生物经过多代繁殖后临近灭绝的概 率，p是 关 于x的 方 程p0＋p1x＋p2x2＋p3x3＝x的一个最小正实根，求证:当E(X)≤1时，p＝1，当E(X)＞1时，p＜1;

(3)根据你的理解说明(2)问结论的实际含义.

解析

(1)E(X)＝0×0.4＋1×0.3＋2×0.2＋3×0.1＝1.

(2)证法1(函数零点法)

设f(x)＝p0＋p1x＋p2x2＋p3x3－x(x∈[0，1])，则f′(x)＝p1＋2p2x＋3p3x2－1.

当μ＝E(X)≤1时，对于任意的x∈[0，1]都有f′(x)≤f′(1)＝μ－1≤0，则f(x)在[0，1]上单调递减，又因为f(1)＝p0＋p1＋p2＋p3－1＝0，所以f(x)在[0，1]上有且只有一个零点，故p＝1.

当μ＝E(X)＞1时，对于任意的x∈[0，1]都有f″(x)＝2p2＋6p3x≥2p2≥0，则f′(x)在[0，1]上单调递增.因为f′(0)＝p1－1＜0，且f′(1)＝μ－1＞0，所以f′(x)在[0，1]上有唯一零点λ∈[0，1)，当x∈[0，λ]时，f′(x)≤0，则f(x)在[0，λ]上单调递减，当x∈(λ，1]时，f′(x)＞0，则f(x)在[λ，1]上单调递增，又因为f(0)＝p0≥0，f(λ)＜f(1)＝0，所以f(x)在[0，1)上有且只有一个零点p∈[0，λ]，故p＜1.

综上所述，当E(X)≤1时，p＝1;当E(X)＞1时，p＜1.

证法2(因 式 分 解 法)p0＋p1x＋p2x2＋p3x3＝x，由p0＋p1＋p2＋p3＝1，得

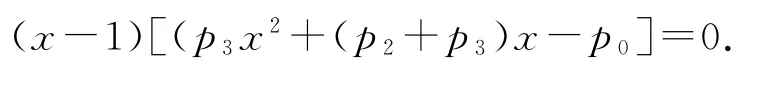
设f(x)＝p3x2＋(p2＋p3)x－p0，则f(x)的对称轴又f(0)＝－p0＜0，f(1)＝p1＋2p2＋3p3－1＝E(X)－1，所以当E(X)≤1时，f(1)≤0，故f(x)的正实根大于或等于1，故原方程的最小正实根p＝1;当E(X)＞1时，f(1)＞0，故f(x)的正实根小于1，故原方程的最小正实根p＜1.

(3)意义:每一个该种微生物繁殖后代的平均数不超过1，则若干代必然灭绝，若繁殖后代的平均数超过1，则若干代后被灭绝的概率小于1，该微生物会多代繁殖下去.

点评

表面看这属于灭绝概率问题，但经过分析发现是三次函数问题，不管是零点分析法，还是因式分解法，都是用函数思想进行研究，应用导数求得其最小值点.

2.6 偶然与必然，呈现问题规律

概率统计研究过程是在偶然中寻找必然，再用必然规律解决偶然问题.主要是收集数据、整理数据和分析数据等处理数据的能力，从数据中提取信息，用信息说明问题、下结论或者分析结论，从而用数据说话.

例6(2021年新高考Ⅰ卷18)某学校组织“一带一路”知识竞赛，有A，B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束.A类问题中的每个问题回答正确得20分，否则得0分;B类问题中的每个问题回答正确得80分，否则得0分.

己知小明能正确回答A类问题的概率为0.8，能正确回答B类问题的概率为0.6，且能正确回答问题的概率与回答次序无关.

(1)若小明先回答A类问题，记X为小明的累计得分，求X的分布列;

(2)为使累计得分的期望最大，小明应选择先回答哪类问题?请说明理由.

解析

(1)由题可知，X的所有可能取值为0，20，100，则

因此，X的分布列如表2所示.

表2

(2)由(1)知，E(X)＝0×0.2＋20×0.32＋100×0.48＝54.4.若小明先回答B类问题，记Y为小明的累计得分，则Y的所有可能取值为0，80，100，有

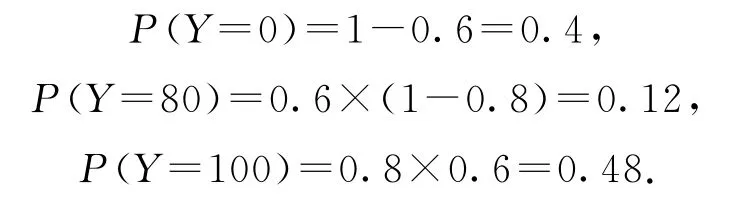
所以E(Y)＝0×0.4＋80×0.12＋100×0.48＝57.6.因为54.4＜57.6，所以小明应选择先回答B类问题.

点评

通过“分布”与“期望”两个方面获取随机变量的规律，在偶然中寻找必然，在寻找规律的过程中，还要求样本均值、样本方差、相关系数等，比如，2021年全国甲卷理科第17题考查了2×2列联表，要求根据数据求K2，以判断甲、乙机床的质量差异.