基于土体连续性作用下挡土墙动力响应的显式闭合形式解

陈青生， 胡 赟， 可文海， 徐长节,2， 彭泽文

(1.华东交通大学 江西省岩土工程基础设施安全与控制重点实验室，南昌 330013；2.浙江大学 滨海和城市岩土工程研究中心，杭州 310058)

挡土墙的地震分析和设计是岩土地震工程中的一个重要领域，受到了广泛的关注。挡土墙可防止高地势土体变形失稳导致掩埋运输设施和附近建筑物[1-5]。然而，在现场勘查中经常可以观察到挡土墙在地震动力响应作用下倒塌现象[6-9]。因此，对岩土工程的设计，必须始终将安全放在首位，而准确分析动力响应作用下挡土墙-土相互作用显得至关重要。

Scott[10]提出了一种简单的方法来确定挡土墙上的土动力响应，引入了一系列独立的Winkler弹簧来解释动力响应下的墙-土相互作用。但是，由于忽略了土体的连续性作用，Scott模型精度较低，因此在应用过程中受到很大限制[11-12]。为了克服这个问题，许多学者致力于开发许多新方法。Zhang等[13]提出了一种新的模型来揭示土体连续性作用的影响，并发现它可能主导土与结构的动力相互作用。Veletsos等运用Lagrange方程，并考虑了土体连续性作用[14]，提出了一种连续介质模型来求解挡土墙的动力响应，从而提高了计算精度，但是计算比Scott的模型复杂得多[15]。 Wood[16]通过弹性动力学基本理论对水平向S波激励作用下的挡土墙动力响应进行了研究，但计算非常复杂，且仅考虑了刚性挡土墙的动力响应。周晓岩[17]基于解耦的近场波动模拟技术，研究了地震作用下挡土墙的动力响应。应宏伟[18]对挡土墙-土系统进行波动有限元分析，得到了水平地震作用沿挡土墙结构高度的分布规律。

在过去的几十年中，Pasternak模型由于其简单性和准确性而被广泛用于分析土与结构的相互作用[19]。与Scott模型相比，Pasternak模型通过引入剪切刚度系数γ在土与结构之间形成一个剪切层，该刚度因子能够考虑土体连续性的影响。尽管引入了系数γ，但Pasternak模型的解的形式仍与Scott模型一致，使得 Pasternak模型不仅保留了连续介质模型动力解的主要优点，而且在数学形式上也较简单[20-21]，因此，Pasternak模型在桩-土动力响应及挡土墙-土动力响应分析中被广泛应用。刚度系数k和剪切刚度系数γ是评估挡土墙变形的两个关键参数，直接影响模型的准确性。然而，迄今为止，由于求解过程复杂，计算迭代繁琐，仍然很难基于Pasternak模型来获得剪切刚度系数γ的精确的表达式，大幅度地限制了其在工程上的应用。

为解决上述问题，本文提出一种基于Pasternak 模型的简明解析解来研究挡土墙的动力响应，其中通过修正Vlasov模型来求解刚度系数k和剪切刚度系数γ，并分析位移衰减函数及在不同相对柔度系数和相对转度系数下入射波频率对挡土墙-土系统内力的影响，阐述入射波频率对挡土墙-土系统动力响应的影响。本文模型不仅传承了Scott模型的简便性，还考虑了土体连续性作用的影响。通过将结果与现有连续介质模型和Scott模型获得的结果进行比较，有效地验证了所提出模型的准确性。

1 分析方法

1.1 挡土墙-土系统的微分方程

地震作用下挡土墙-土系统动力响应计算示意图如图1所示，该系统经受垂直入射的S波，其振幅为ur且频率为ω。回填土可视为各向同性的黏弹性材料，挡土墙视为线弹性欧拉-伯努利梁。挡土墙-土模型认为是平面应变问题，土体在水平方向上是无限的。在下文的分析中，挡土墙与土是紧密接触，不存在任何形式的滑移和脱离，即挡土墙与土在界面处位移连续。

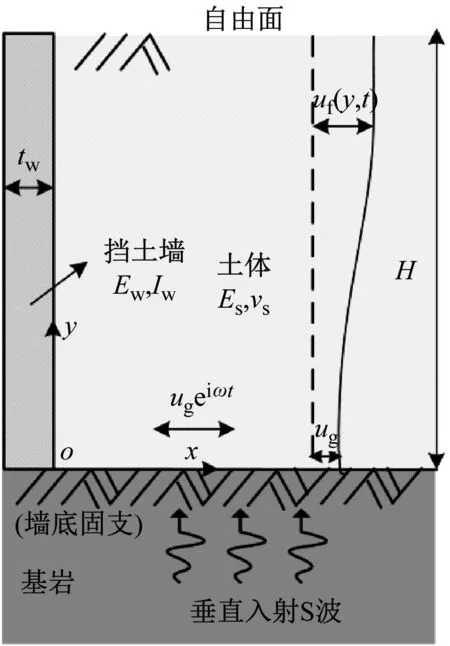
(a)

如图2所示，用Pasternak模型表示挡土墙-土相互作用。与Scott模型相比，引入了一个刚度为γ的附加剪切层，以考虑周围土体的连续性作用。考虑到谐波激励作用下挡土墙单元上的水平力平衡，基于Scott模型的挡土墙-土系统的动力响应可以表示为

(1)

考虑到土体的连续性，基于Pasternak模型增加刚度系数γ。式(1)修改为

(2)

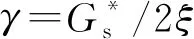
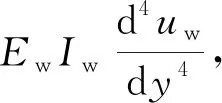
此外，式(2)可以进一步简化为

(3)

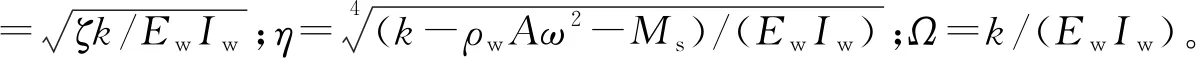
同时，式(3)的通解可写为

(4)

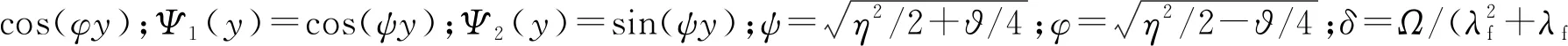
(a) 挡土墙-土动力相互作用

挡土墙墙底固支的动力响应的边界条件可以表示为

(5)

(6)

(7)

uw=ur,y=H

(8)

将式(5)～式(8)代入式(4)，求得未知常数Δi。

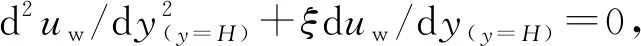
(9)

将边界条件式(5)～式(8)代入式(9)，求得未知常数Λi。

最后获得了挡土墙动力响应的显式封闭形式解，如表1所示。可见，与Scott的模型相比，本文大幅度地简化解析解的模式。同时，本文提出的模型不仅传承了Scott模型的简便性，还考虑了土体连续性作用的影响。为了验证本文模型的精确性，下文进一步展开对比分析。

表1 本文模型与 Scott 模型之间的公式比较

1.2 设计参数

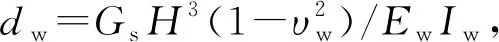
此外，Fan等[23]提出一个无量纲参数Iu=uw(0)/uf(0)。通过比较地下结构位移和地表动力矩，Iu可以反映地下结构-土动力相互作用的强度，故可称为水平位移下动力响应因子。类似的，转动下动力响应因子Iφ的表达式可表示为Iφ=uw(0)/λuf(0)。

因子ζ是修正Vlasov模型中的一个迭代因子，无法直接求解。ζ与相对柔度系数dw和S波频率ω密切相关。在大多数情况下，dw范围为1～40，dθ范围为0.5～10.0，ω范围为0～2ω1)，基于修正Vlasov模型的迭代程序的计算结果，因子ζ大约等于0.2。

为了进一步研究各物理参数对挡土墙动力响应的影响，对式(2)进行了详细的研究。由式(2)的描述，挡土墙-土动力相互作用中的各物理量包括：挡土墙抗弯刚度作用(Fbp)；土体连续性作用(Fss)；土弹簧作用(Fwm)；土体惯性力(Fis)；挡土墙惯性力(Fiw)，可被分别表示为

(10)

(11)

Fwm|y=0=k(uw-uf)

(12)

Fis|y=0=-Msω2(uw-uf)

(13)

Fiw|y=0=-ρwtwω2uw

(14)

2 模型验证

为了解决挡土墙动力响应问题，验证本文模型的有效性和正确性，将所提出模型的结果与Veletsos等的连续介质模型及Scott模型的结果进行比较，结果见图3。

从图3(a)中可以看出，用本文方法求得的挡土墙位移与 Veletsos等的连续介质模型吻合较好，这主要是由于本文模型已将土体连续性作用对挡土墙动力响应影响相结合，仍有差异是因为Veletsos等的解是由系统中总位移的模态构成的，而本文只采用的全位移中的第一阶模态来表示。Ke等也观察到了在桩的动力响应有类似现象。而Scott模型的所有曲线都低于本文模型和Veletsos等的连续介质模型，这可能是由于土体连续性作用作为约束力来约束挡土墙的动力响应。

图3(b)表明，随着基岩对挡土墙的约束减弱(即相对转度系数dθ从0.5增加到5.0)，本文模型与Scott模型对应的曲线之间的差异显著增大。这是因为，对于旋转柔度系数较大的墙，挡土墙-土相互作用的影响更加显著。结果表明，土体连续性作用对挡土墙的动力响应有显著影响。

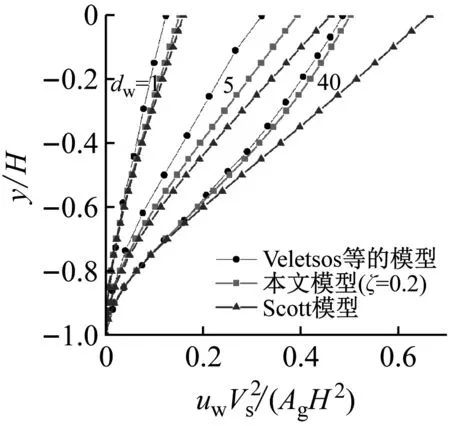
(a) dw不同的曲线

3 位移衰减函数

由(4)式可知，位移函数uw(y)和衰减函数φ(x)是耦合在一起。而因子γ直接影响衰减函数φ(x)，可以顺利地把挡土墙的位移uw(y)解耦出来。为解决挡土墙-土系统中任一点的位移问题，进一步分析γ与衰减函数φ(x)的关系显得尤为重要。

由弹性力学的基本理论可得，挡土墙-土相互作用系统的势能表示为

(15)

类似的，系统的动能可以表示为

T=T挡土墙+T土体=

(16)

由Hamilton原理

(17)

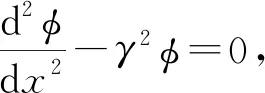
(18)

将边界条件代入，可得衰减函数为

φ(x)=e-γx

(19)

由式(9)得知衰减函数是确定挡土墙-土系统位移函数的重要组成部分，而衰减函数影响着位移衰减的快慢。图4给出了衰减函数的变化，结果表明因子γ决定着衰减函数变化的快慢，随着γ的逐渐增大，衰减函数沿x方向衰减越快。

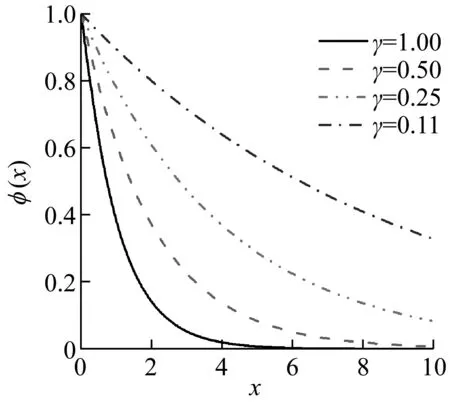
图4 衰减函数随x变化曲线

可见，因子γ对衰减函数φ(x)影响显著，准确确定因子γ对解决挡土墙-土动力相互作用的平面应变问题起着关键作用。

4 参数分析

在实际工程中，挡土墙的内力和变形是极为重要的参数，为了探究入射波频率对挡土墙内力和变形因子的影响，本文选取不同相对柔度系数和相对转度系数，进一步对挡土墙的剪力、弯矩和变形因子进行参数分析。

相对柔度系数变化下不同入射波频率对挡土墙平动因子Iu和转动因子Iφ的影响如图5所示。在入射波频率较小时，随着入射波频率的增大，Iu减小而Iφ却呈现增大趋势，并且dw越大，Iu下降幅度更小而Iφ增大幅度更大。在入射波频率较大时，Iu和Iφ均呈现复杂性变化。

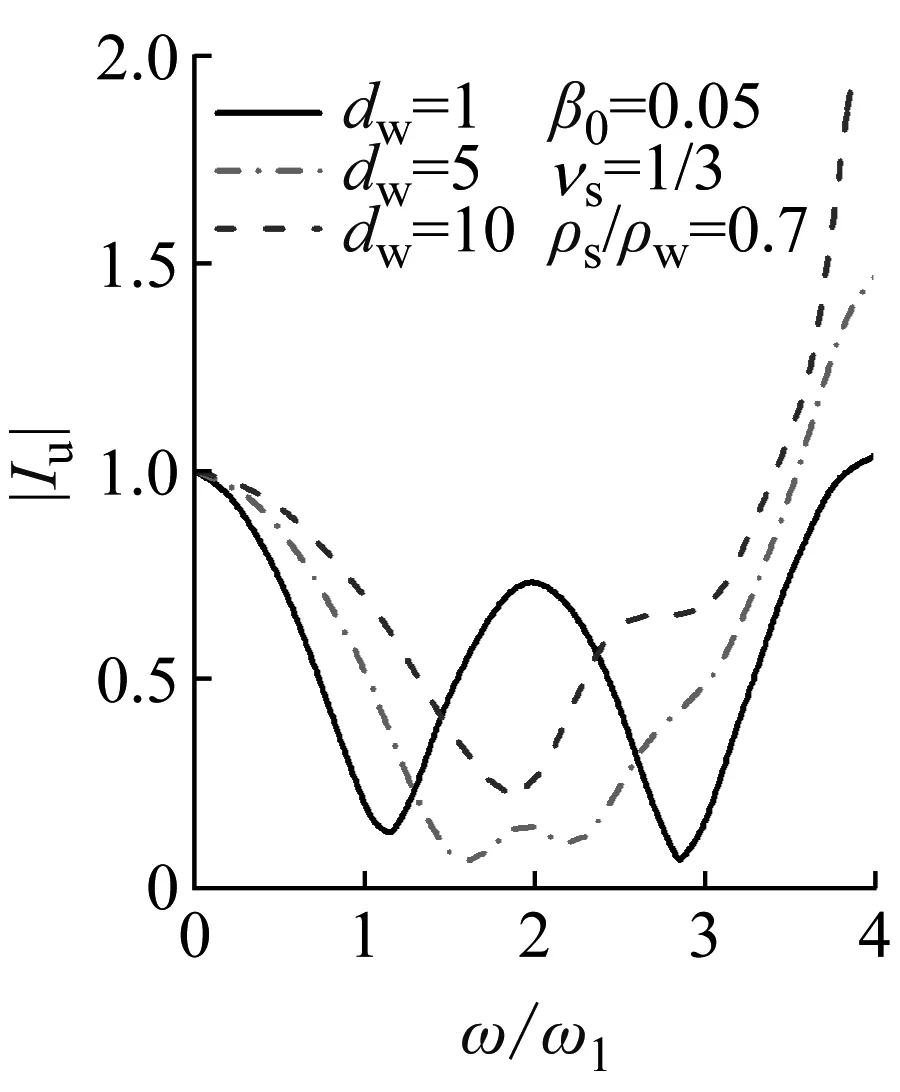
(a)

图6给出了在不同无量纲相对柔度系数dw下入射波频率对挡土墙底剪力和弯矩的影响。挡土墙底的剪力和弯矩可以归一化表示为Qb=Ql/(xgρsH2)和Mb=Ml/(xgρsH3)。可以看出，剪力和弯矩均呈现非线性变化，当入射波频率接近ω1和3ω1时，挡土墙-土系统容易出现共振现象。在入射波频率较小的情况下，随着dw的增大，剪力和弯矩均呈现下降的趋势，但当入射波频率较大时，这种情况恰好相反。这可能是由于对软土而言，地震作用的放大效应造成的，这种现象类似于地震作用下桩-土动力响应。得出，入射波频率对于挡土墙内力有着重大影响，尤其是当入射频率接近自振频率时，这种现象更明显。

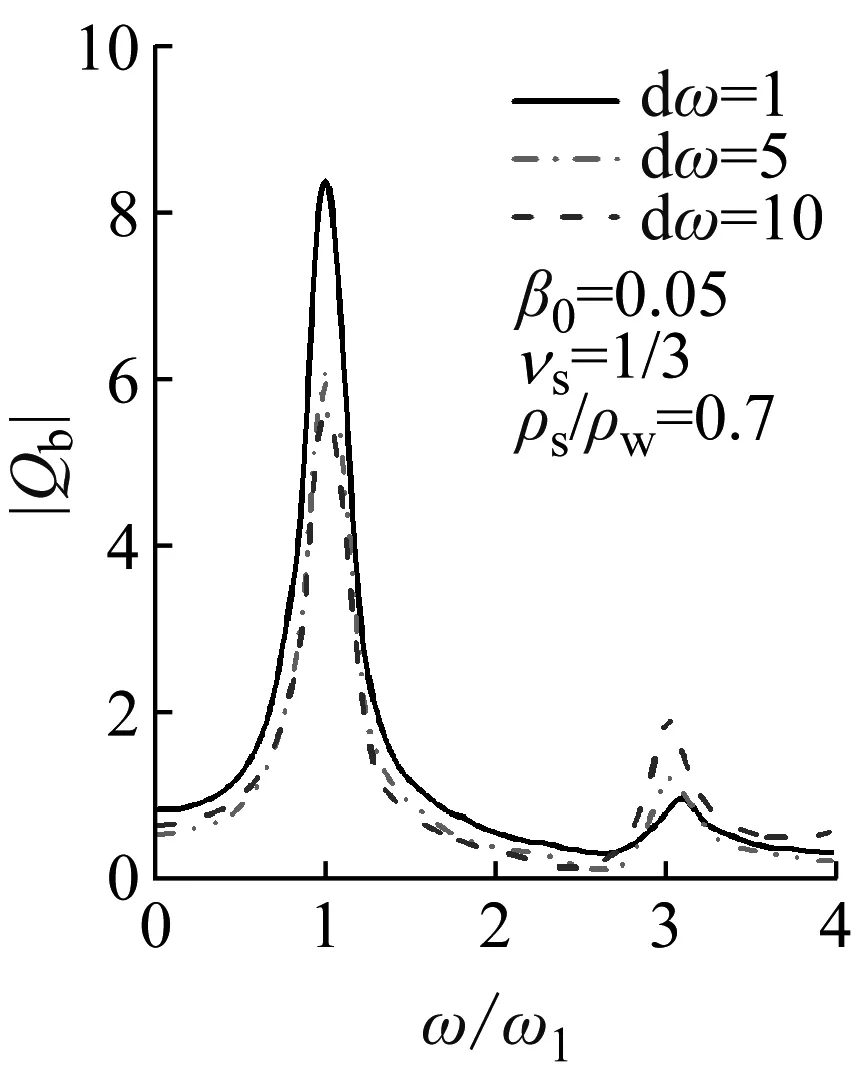
(a)

在不同无量纲相对转度系数dθ下入射波频率对挡土墙底剪力和弯矩的影响如图7所示。与不同dw下的类似，剪力和弯矩均呈现非线性变化，挡土墙-土系统在入射波频率接近ω1和3ω1时容易出现共振现象。在入射波频率较小的情况下，随着dθ的增大，剪力和弯矩均呈现下降的趋势。对dθ不变时，墙底剪力和弯矩均呈现随入射波频率增大，出现先增大后减小再增大再减小的现象。再次验证了，入射波频率对于挡土墙内力有重大影响。

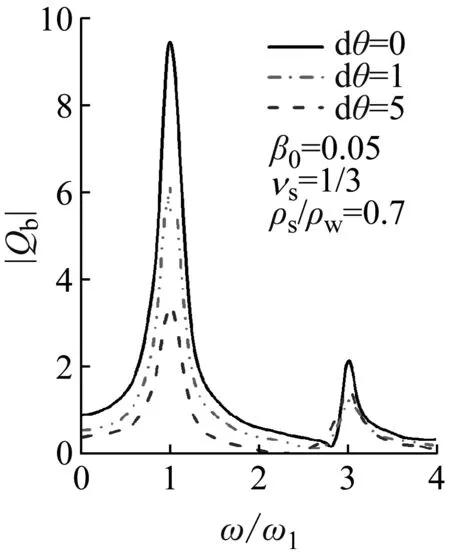
(a)

从图6和图7中可以看出，在相同入射波频率下，不同的dw和dθ将导致剪力和弯矩存在明显的差异，即在不同的约束条件下，挡土墙的动力响应有较为明显的差别。

5 结 论

综上所述，可得到以下结论:

(1) 在平面应变和忽略了竖向位移对系统的影响的前提假设下，提出一个新的位移函数的显式闭合形式解，用以解决墙底固支和墙底铰支挡土墙在垂直入射S波作用的挡土墙-土的动力响应，并得到挡土墙-土动力相互作用中各物理量的精确表达式。

(2) 以一系列刚度会被入射波频率影响的土弹簧与土膜模拟土体连续性，将所得位移函数与Veletsos等及Scott模型求解的结果进行对比分析，很好地验证了本文模型的有效性和准确性。

(3) 在入射波频率接近ω1和3ω1时，不论是墙底固支还是铰支，挡土墙-土系统均容易出现类似共振的现象，且剪力和弯矩均呈现范围内峰值，尤其是当入射频率接近ω1时，这种现象更明显。

(4) 平动因子Iu和转动因子Iφ对入射波的频率十分敏感，同时挡土墙的相对柔度系数对其也有很大影响，而墙底的剪力和弯矩对挡土墙的相对柔度系数dw和相对转度系数dθ以及入射波频率十分敏感，挡土墙-土相互作用越剧烈，同时，不同约束条件也对挡土墙的动力响应较大有影响。