波浪锥型圆柱流固耦合振动机理研究
2022-02-22杨耀宗列煜俊徐劲力
邹 琳, 秦 傲, 杨耀宗, 列煜俊, 徐劲力
(武汉理工大学 机电工程学院, 武汉 430070)
圆柱绕流涡激振动一直是工程领域广泛关注的热点,之前学者的研究主要集中在探究圆柱绕流涡激振动机理及如何将圆柱的锁频区间变窄,抑制涡激振动的发生[1-2]。周国成等[3]探究了不同刚度系数对二维圆柱涡激振动的影响。Bahmani等[4]发现系统质量比或阻尼比降低会导致振幅和锁频区间增加,圆柱下游出现“2S”模式的涡旋脱落(以下简称涡脱),与Williamson等[5]的研究结果相一致。邹琳等[6]对不同间距比的二维串列双圆柱进行了涡激振动响应特性研究,研究了在双自由度条件下下游圆柱的锁频区间、振动频率等特性。康庄等[7]研究了低质量比条件下,雷诺数对圆柱涡激振动的影响规律。唐友刚等[8]发现顺流向振动会对横流向振动产生影响,且顺流向振动的振幅也会增大。陈威霖等[9]研究发现圆柱串列排列时,由于圆柱之间的耦合作用,圆柱会出现不同类型的涡激振动响应,流体力也呈现不同的变化。Zhang等[10]在雷诺数Re=5 000时对波浪型圆柱涡激振动与固定绕流进行比较,发现在零结构阻尼的情况下,波浪形状表面对减缓流动引起的振动具有一定效果。
显然柱体表面的形状直接影响流场结构及其振动,因此探究何种参数的柱体表面可以产生更加宽泛的振动区间和更大的振动幅度是提高无叶片风力发电的关键。本文将波浪型圆柱和锥型圆柱相融合形成波浪锥型圆柱,探究波浪锥型圆柱的耦合振动机理,使波浪锥型圆柱具有更好的振动响应特性,为无叶片风力俘能结构涡致振动的增大和发电效率的提升提供理论支持。
1 几何模型及数值方法
1.1 几何模型
基于Lam等[14]的研究,本文提出将波浪型圆柱和锥型圆柱相融合形成波浪锥型圆柱,波浪锥型圆柱母线余弦波随着高度Z的增加具有一定的斜率k,主要的几何特征可用式(1)和式(2)描述为
(1)
Dm=(Dmax+Dmin)/2
(2)
k=(Dmax-Dmin)/2H
(3)
式中:DZ为波浪锥型圆柱在展向方向(Z坐标)上的横截面直径;Dmax和Dmin分别为锥型圆柱截面的最大和最小直径;Dm为波浪锥型圆柱的平均直径;α为余弦波浪的波幅;λ为余弦波浪的波长;k为余弦波浪的倾斜斜率;H为波浪锥型圆柱的高度,在本文中,高度为7Dm,选取展向中间位置为平均直径Dm=0.01 m。波浪锥型圆柱每个波长内的最大直径截面和最小直径截面分别命名为Node和Saddle;波浪锥型圆柱的几何参数以及流场计算域的大小进行无量纲时均采用平均直径为单位,如图1所示。图1中DL和DH分别为锥型圆柱底段和顶端截面直径。本文所计算的几种波浪锥型圆柱参数,如表1所示。
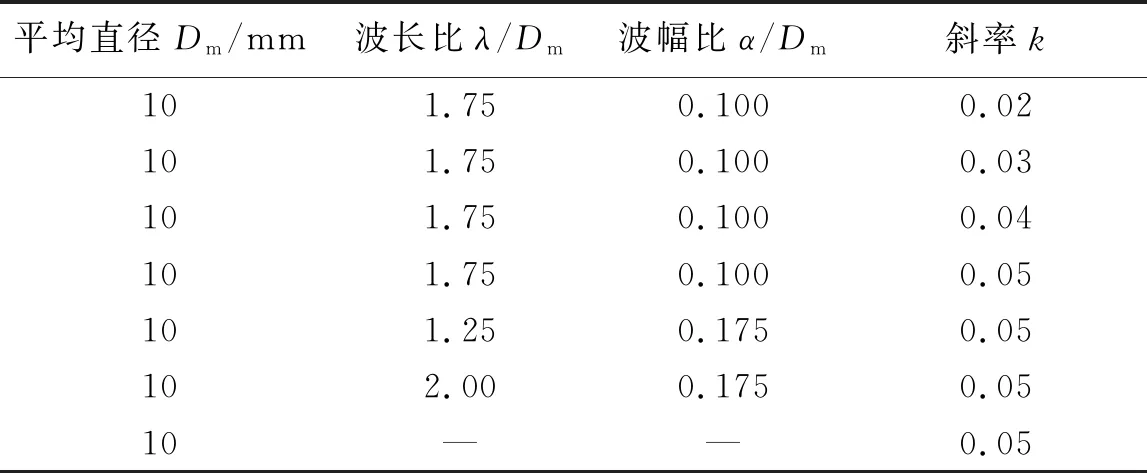
表1 波浪锥型圆柱相关参数
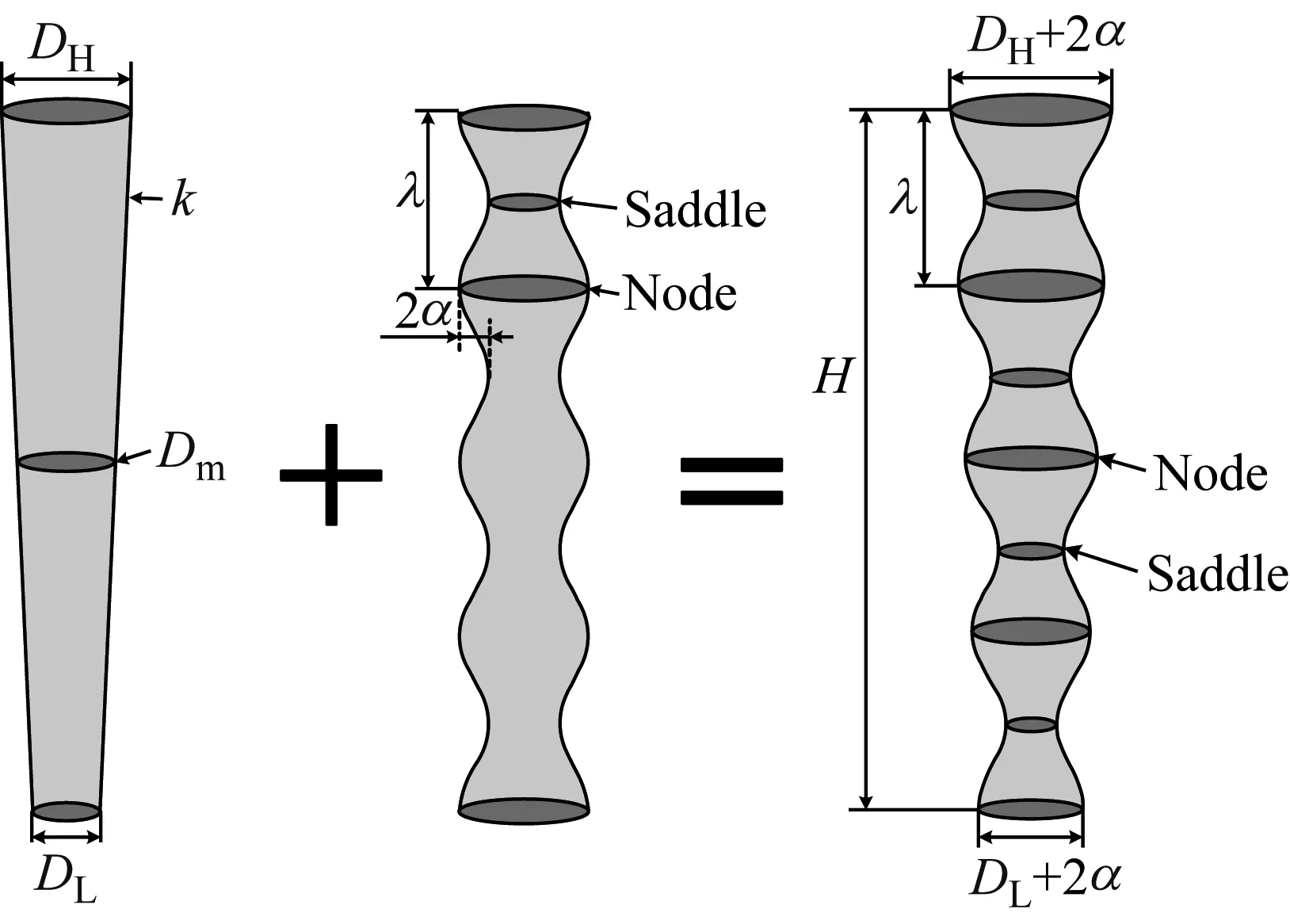
图1 波浪锥型圆柱结构示意图
1.2 数值计算方法及计算域
在涡激振动模型中,本文通过用户自定义函数(user-defined-function,UDF)控制网格的变形与运动,将波浪锥型圆柱的涡激耦合振动简化为弹簧阻尼系统
(4)
式中:y(t)为波浪锥型圆柱的位移,变量上的点为对时间的导数;m为波浪锥型圆柱的质量;c为系统的阻尼系数;g为系统的弹性刚度;Fy为波浪锥型圆柱受到流体施加的作用力。
在网格更新过程中首先使用Compute_Force_and_Moment宏定义获取波浪锥型圆柱所受外力;然后再根据四阶龙格-库塔法计算出波浪锥型圆柱的位移和速度;最后将求得的横向位移和速度用于更新网格。本文采取重叠网格的方法,因此使用DEFINE_ZONE_MOTION宏定义控制组件网格区域的整体运动。
截止到2018年12月,在装有Android系统的手机等设备的应用界面,以“俄语”、“俄罗斯”为关键词搜索相关软件(不包括游戏),只有十几款。那么,俄语等级测试APP的现状就更不容乐观了。市场上可供使用的俄语等级测试APP的现状如下:只针对俄语等级测试的APP只有Bears这一款。俄语7500km虽然也涉及俄语等级测试的内容,但其全部内容却包括俄语学习的方方面面,比较宽泛。而俄语研习社、俄语摆渡专八刷题宝典、俄语堂虽同样包括俄语等级测试的内容,但皆属于微信小程序,需要依托微信平台(但微信小程序除需借助微信平台外,其他大体上与APP相似,所以在这里一并进行了分析)。
在参考Lam等流场计算域的大小之后,本文将波浪锥型圆柱计算域的大小确定为30.0Dm×20.0Dm×10.0Dm,X坐标轴为顺流向方向,Y坐标轴为横流向方向,Z坐标轴为展向方向。以波浪锥型圆柱底面圆心为坐标系原点,在顺流向方向上,上游入口边界距离原点10.0Dm,下游出口边界距离原点20.0Dm;在横流向方向上,两侧边界距离原点10.0Dm;在展向方向上,底部边界距离原点为1.5Dm,如图2所示。这样设置即保证了流体到达波浪锥型圆柱表面时为均匀流,又避免了计算域边界对波浪锥型圆柱周围流场状态的干扰。
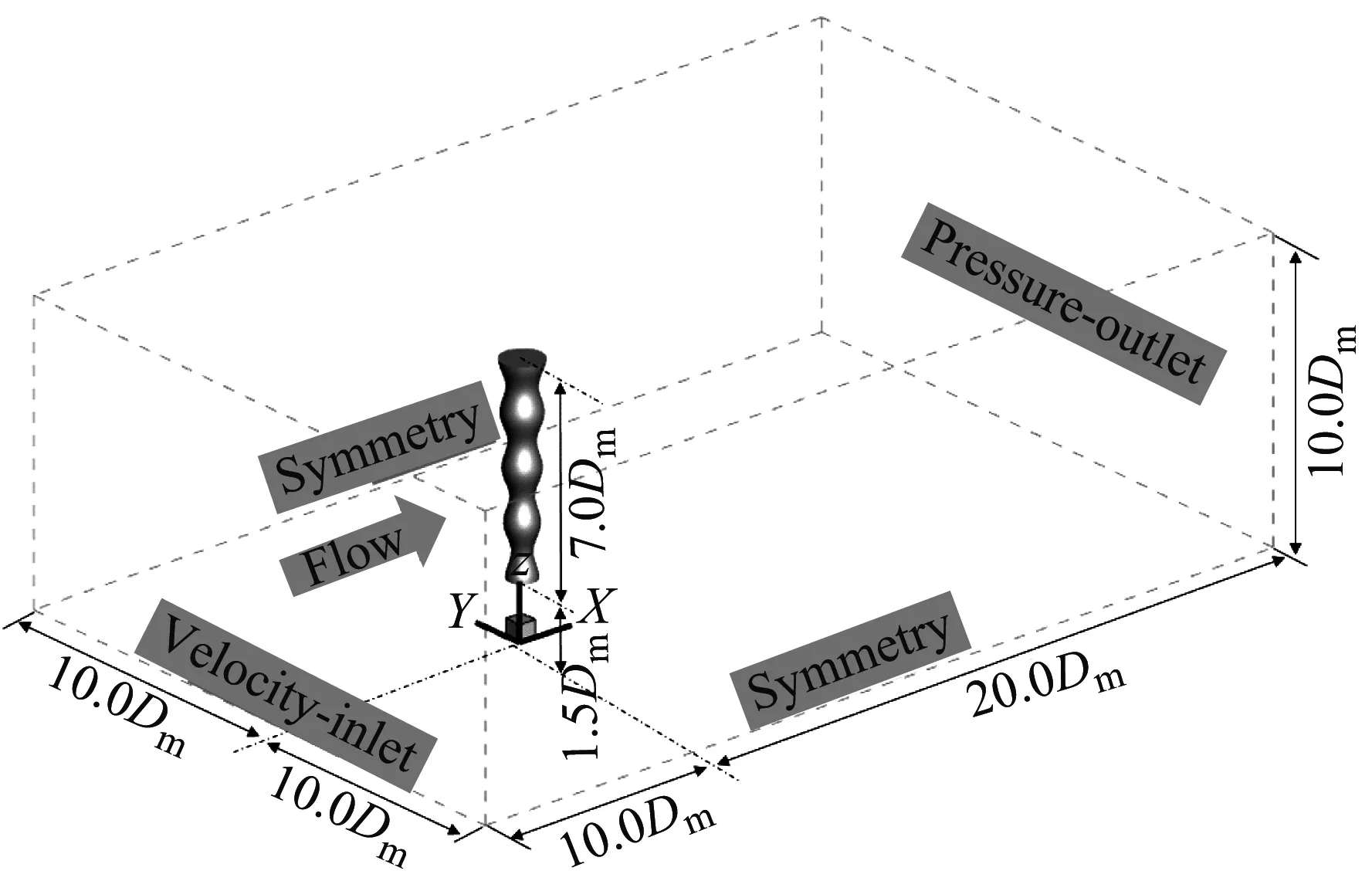
图2 波浪锥型圆柱计算域
边界条件设置:上游入口边界采用均匀速度入口边界,在Re=3 900的条件下,入口速度为5.772 m/s;下游出口边界设置为压力出口边界,相对压力为0;左右两侧、底部以及顶部边界均设置为对称边界;波浪锥型圆柱表面设置为无滑移壁面。
1.3 计算模型及程序试验验证
取单个直圆柱进行单自由度涡激振动的数值模拟与试验验证,并将仿真和试验结果与文献作对比以验证计算模型和UDF程序的正确性。
试验示意图,如图3所示。该风洞试验段截面尺寸为450 mm×450 mm,试验段的前后壁面各有直径为280 mm的可拆卸盖板,边界层厚度为18 mm左右。直圆柱的试验模型根据工程实例按6∶1等比例放大,直径为60 mm,风洞中的长度为445 mm,模型上下两端各伸出50 mm,在延长段两侧都开有小孔方便悬挂弹簧,根据雷诺数相似准则调整进风口风速。试验装置如图4所示。试验物件采用3D打印技术,因此试验物件的质量比m*=15.8。
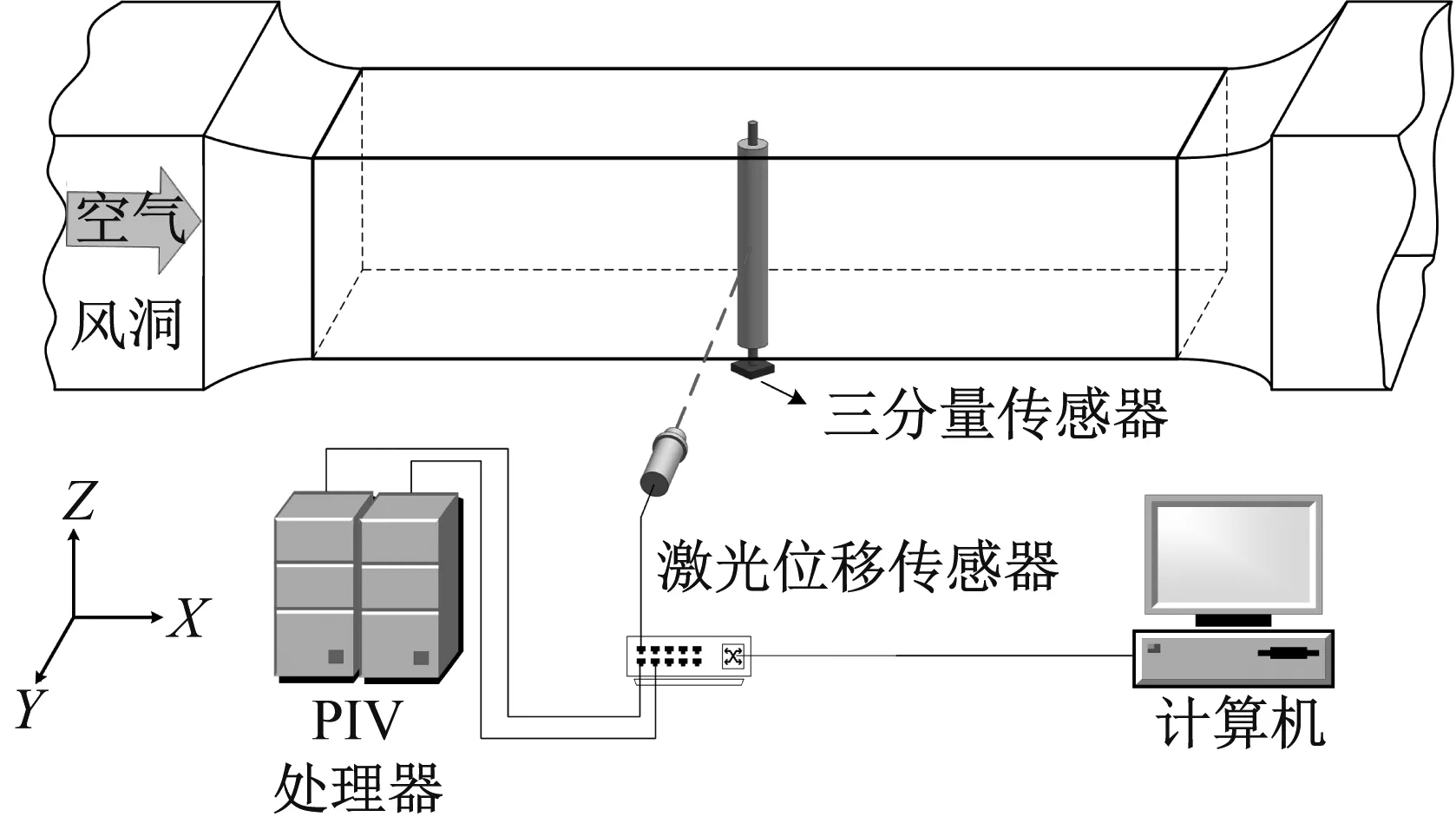
图3 试验示意图

图4 试验装置布置图
单自由度圆柱最大振幅比随折合流速Ur变化的变化曲线,如图5所示。由图5可知,仿真结果与汪秒[15]的研究结果非常接近。由于试验件的质量比m*=15.8和附加质量的存在,使试验最大振幅比比仿真结果大30.8%,但是其锁频区间以及整体趋势变化一致,因此可以认为本文的计算模型和UDF程序是正确可靠的。
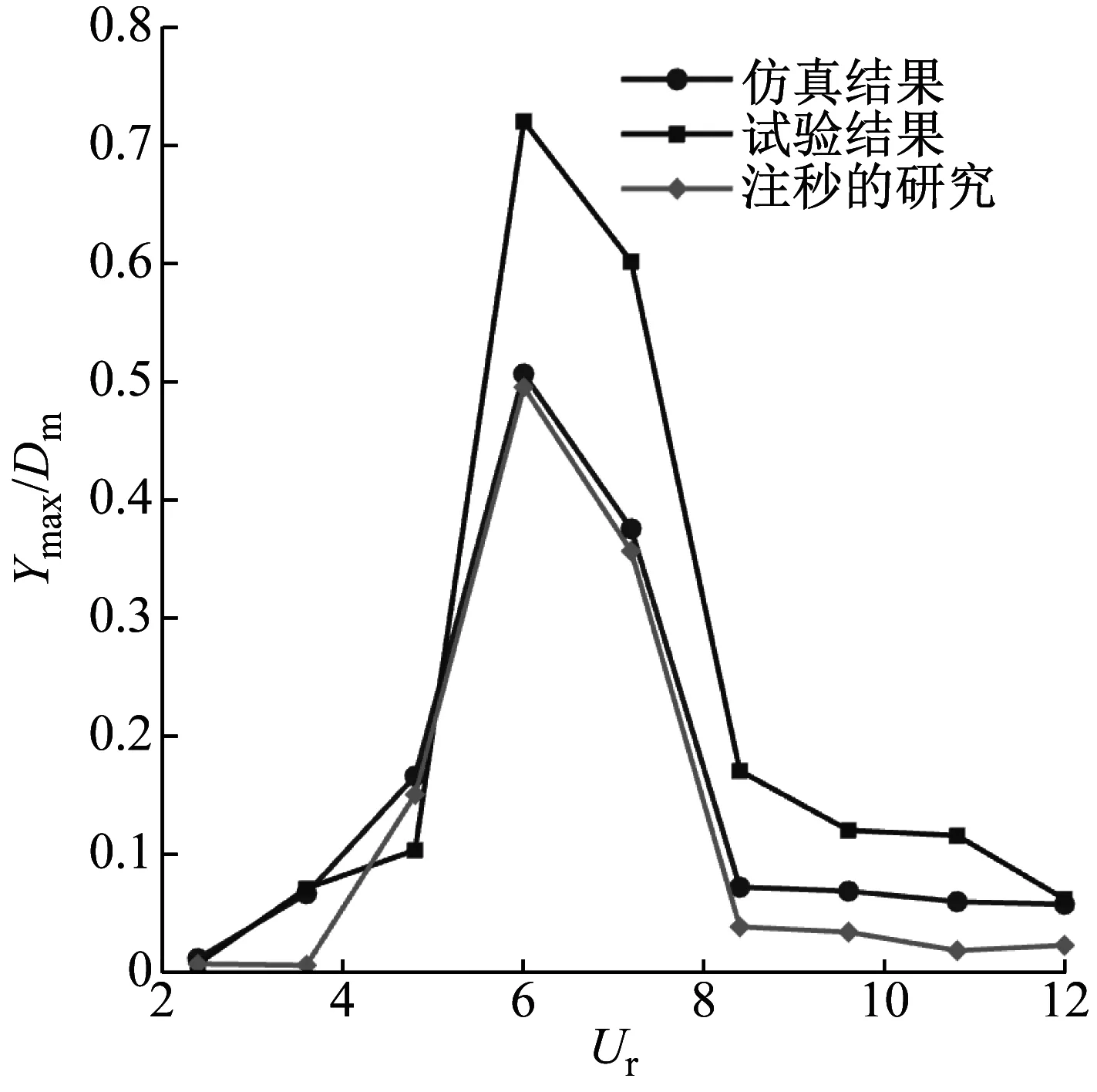
图5 单自由度圆柱涡激振动随折合流速Ur的变化情况
2 计算结果及分析
2.1 振动响应特性分析
不同波长比、不同波幅比、斜率k=0.05和波长比λ/Dm=1.75、波幅比α/Dm=0.10、不同斜率的两个系列的波浪锥型圆柱最大振幅比Ymax/Dm随折合流速Ur的变化情况,如图6所示。
由图6可知:当折合流速Ur<6.0时,直圆柱的最大振幅比Ymax/Dm基本保持在0附近;当Ur=6.0时,直圆柱的最大振幅比Ymax/Dm开始急剧上升,并且在折合流速Ur=8.4时,最大振幅比达到最大值Ymax/Dm=0.841;随后随着折合流速的增大最大振幅比开始逐渐减小,当折合流速Ur>10.8时,最大振幅比开始急剧减小到0附近。这说明直圆柱在折合流速Ur=4.8~6.0时开始进入锁频区间,在折合流速Ur=10.8~12.0时开始退出锁频区间。对于斜率k=0.05的锥型圆柱和不同波长比、不同波幅比、斜率k=0.05的波浪锥型圆柱,当折合流速Ur<6.0时与直圆柱相似,最大振幅比维持在0附近;当6.0
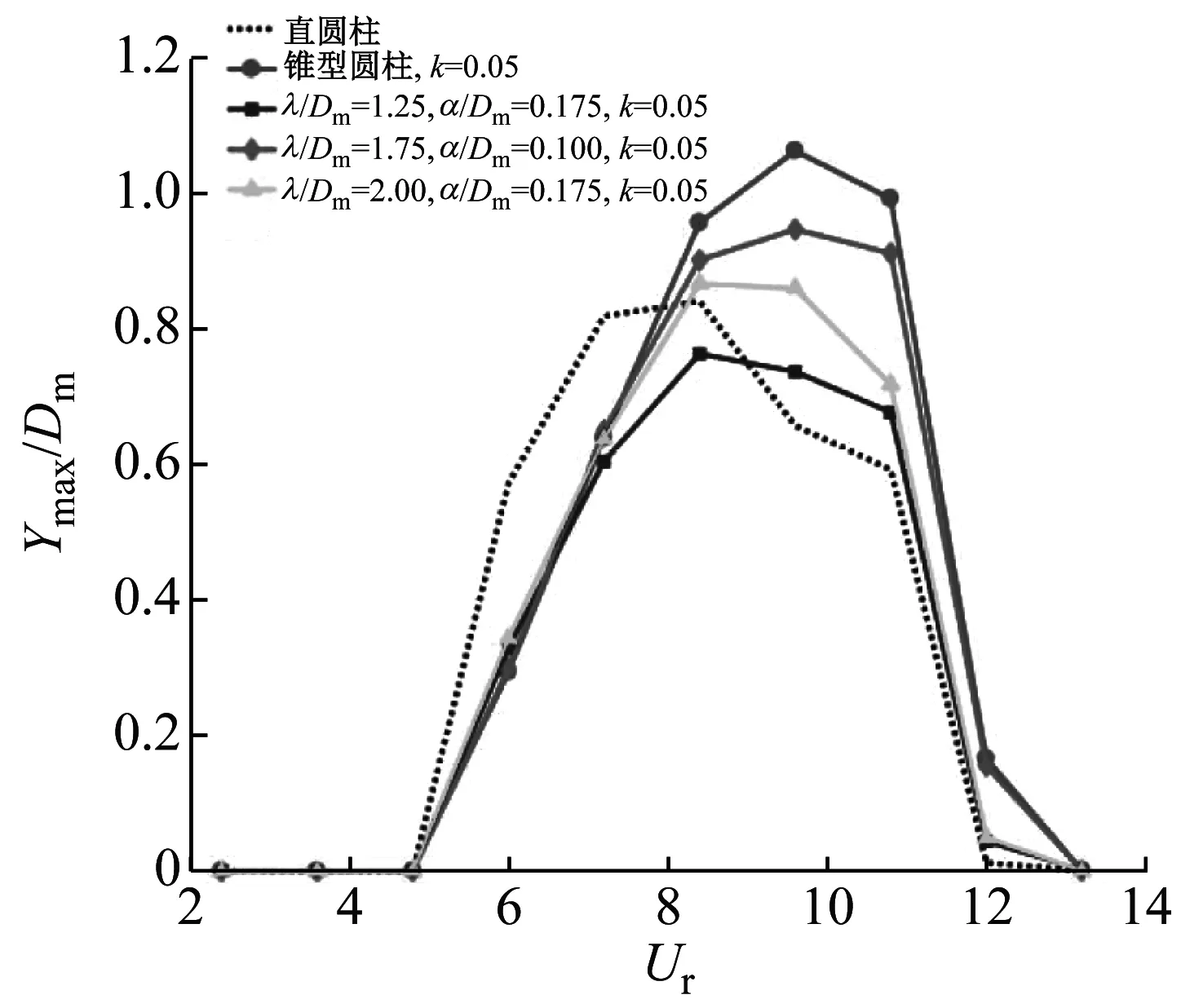
(a)
由图6(b)可知:波长比λ/Dm=1.75、波幅比α/Dm=0.10、不同斜率的波浪锥型圆柱最大振幅比随着折合流速Ur的增长变化趋势与直圆柱的变化趋势相似,在折合流速Ur=4.8~6.0时进入锁频区间,在折合流速Ur=10.8~12.0时退出锁频区间。但是波长比λ/Dm=1.75、波幅比α/Dm=0.10,斜率k=0.05的波浪锥型圆柱在折合流速Ur=9.6时,最大振幅比达到最大值,而其他斜率的波浪锥型圆柱最大振幅比均在折合流速Ur=8.4时达到最大值;斜率k=0.02、0.03和0.05的波浪锥型圆柱最大振幅比的最大值均在0.95附近出现,而斜率k=0.04的波浪锥型圆柱最大振幅比的最大值为0.872。
综合图6(a)和图6(b)可知:不同参数的波浪锥型圆柱和直圆柱以及斜率k=0.05的锥型圆柱相比,最大振幅比各不相同。直圆柱的最大振幅比在折合流速Ur=8.4时达到最大值0.841,波长比λ/Dm=1.75、波幅比α/Dm=0.10,斜率k=0.05的波浪锥型圆柱最大振幅比的最大值与直圆柱相比增大12.6%,斜率k=0.05的锥型圆柱与直圆柱相比增大26.4%。这意味着柱体表面的变化对涡激振动的锁频区间基本没有影响,但是对最大振动幅度有影响。
为了更好分析不同参数的振动响应特性,接下来将分析直圆柱、斜率k=0.05的锥型圆柱以及不同参数的波浪锥型圆柱的频率比随着折合流速Ur变化的变化情况,如图7所示。图7中:fs为涡脱频率;fn为系统固有频率。
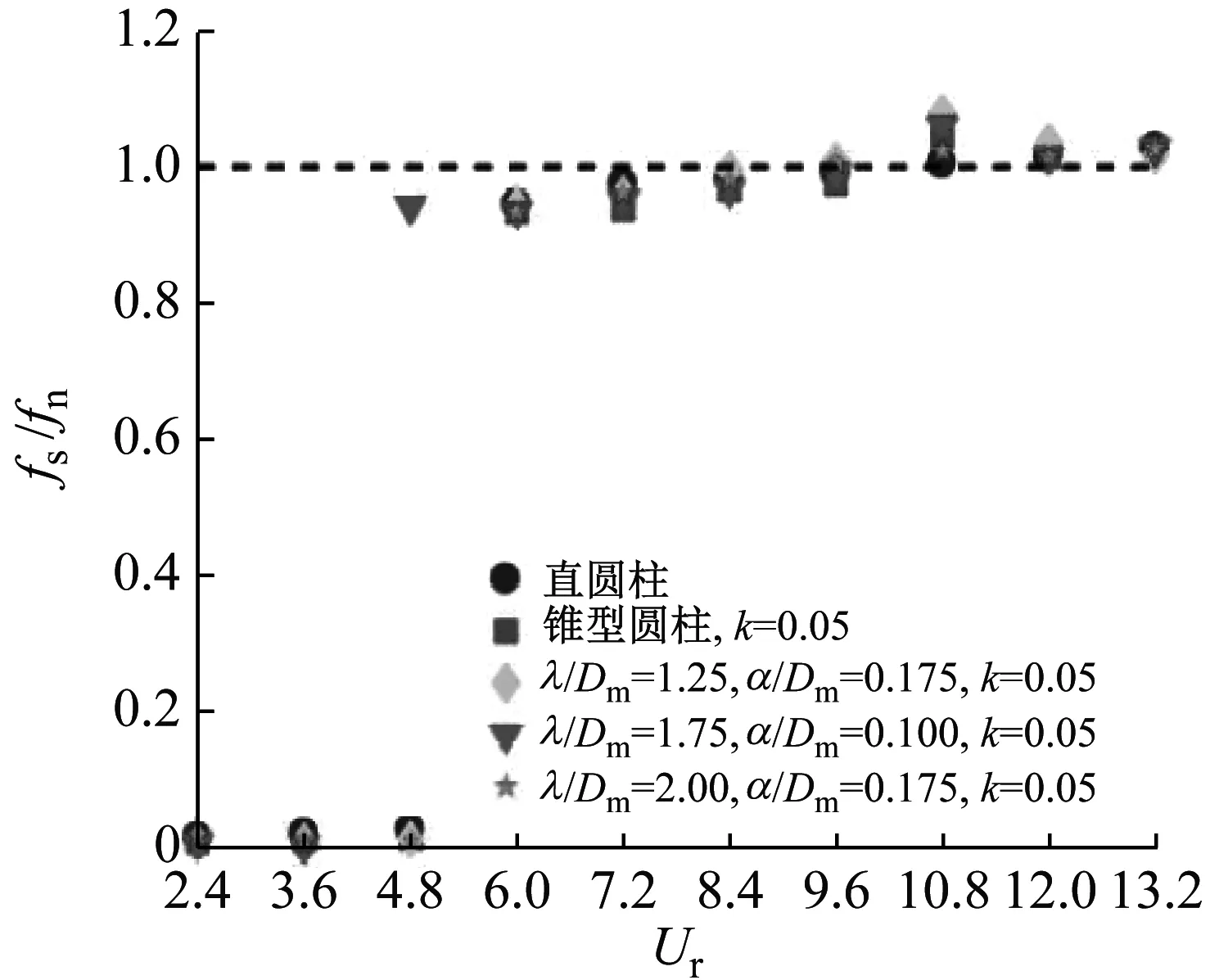
(a)
由图7可知:当折合流速Ur<6.0时,直圆柱、斜率k=0.05的锥型圆柱和各个参数的波浪锥型圆柱其尾流泻涡频率比基本为0;当折合流Ur≥6.0时,尾流泻涡频率比迅速增加到0.93左右,随着折合流速Ur的增大,尾流泻涡频率比缓慢增加,基本维持在1附近,即fs=fn。虽然随着折合流速Ur的增加,尾流泻涡频率比并没有远离1,而是保持在fs=fn附近;但由图6可知,当折合流速Ur>12.0时,波浪锥型圆柱涡激振动已经退出锁频区间,为此,选取波长比λ/Dm=1.75、波幅比α/Dm=0.10、斜率k=0.05的波浪锥型圆柱为研究对象,分析其尾流泻涡频谱图,如图8所示。图8中横轴为频率,纵轴P(f)为功率谱密度。由图8可知:当6.0≤Ur≤10.8时,尾流泻涡频谱的幅值均大于0.04;当折合流速Ur>10.8时,频率的幅值由0.05迅速降低到1×10-4以下,这说明虽然此时尾流泻涡频率与固有频率接近,但是能量很小,不能使波浪锥型圆柱产生共振,从而使波浪锥型圆柱涡激振动迅速退出锁频区间。
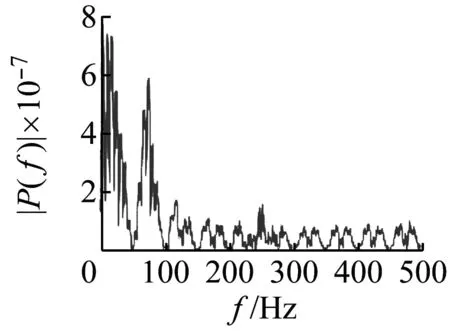
(a) Ur=2.4
2.2 升阻力系数分析
波浪锥型圆柱平均阻力系数随着折合流速增加的变化情况,如图9所示。为了更好的探究波浪锥型圆柱不同参数所产生的影响,分别加入了直圆柱和斜率k=0.05的锥型圆柱作比较。由图9(a)可知:当折合流速Ur<6.0时,折合流速对平均阻力系数基本没有影响,直圆柱和各个参数的波浪锥型圆柱平均阻力系数均保持在0.678附近,而斜率k=0.05的锥型圆柱平均阻力系数却保持在0.481左右,与直圆柱相比降低29.05%;当折合流速Ur=6.0时,直圆柱、锥型圆柱和各个参数的波浪锥型圆柱的平均阻力系数均开始急剧上升,这意味着开始进入锁频区间,直圆柱、锥型圆柱和各个参数的波浪锥型圆柱的最大振幅比也开始快速增大(见图6);随着折合流速的增大,直圆柱在折合流速Ur=7.2时,平均阻力系数达到最大值,而锥型圆柱和波浪锥型圆柱的平均阻力系数在折合流速Ur=8.4时达到最大值,然后随着折合流速的增加开始缓慢下降;当折合流速Ur≥12.0时,平均阻力系数维持在一个稳定的值。而图9(b)表示波长比λ/Dm=1.75、波幅比α/Dm=0.10、不同斜率k的波浪锥型圆柱的平均阻力系数。可以看出平均阻力系数的变化趋势与图9(a)相似,只是平均阻力系数最大值各不相同。
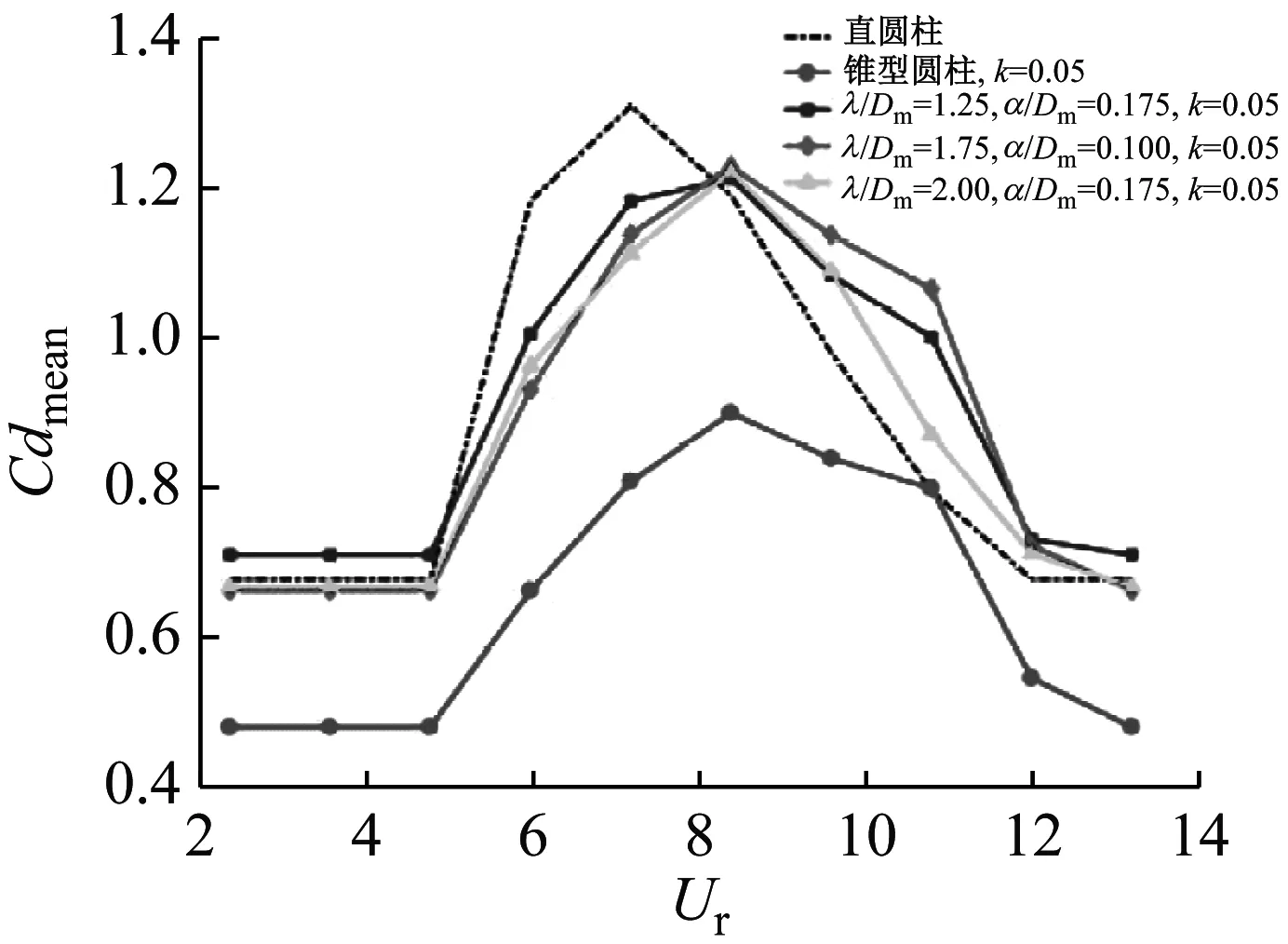
(a)
波浪锥型圆柱脉动升力系数随折合流速增加的变化情况,如图10所示。当折合流速Ur<6.0时,直圆柱、斜率k=0.05的锥型圆柱以及各个参数波浪锥型圆柱的脉动升力系数均为0,此时最大振幅比也基本为0,柱体并没有进入锁频区间。当折合流速Ur≥6.0时,脉动升力系数出现跳跃急剧增加的现象,最大振幅比在相同的折合流速下也出现跳跃,从0开始迅速增大,这意味着直圆柱、斜率k=0.05的锥型圆柱和各个参数波浪锥型圆柱开始进入锁频区间。当折合流速Ur=6.0~9.6时,脉动升力系数随着折合流速的增加迅速降低至0.1附近。当折合流速Ur>9.6时,随着折合流速的增加脉动升力系数缓慢减小并趋于稳定。直圆柱、斜率k=0.05的锥型圆柱以及各个参数波浪锥型圆柱的脉动升力系数在不同折合流速下的最大值,如表2所示。直圆柱和波长比λ/Dm=1.75、波幅比α/Dm=0.10、斜率k=0.02波浪锥型圆柱脉动升力系数的最大值分别达到0.688和0.768。斜率k=0.05的锥型圆柱和其他参数波浪锥型圆柱的脉动升力系数的最大值介于0.40~0.52,这可能是因为最大振幅比不仅仅与脉动升力系数有关,还和平均阻力系数、波浪锥型圆柱表面形状等参数密切相关,是综合相互影响的结果。
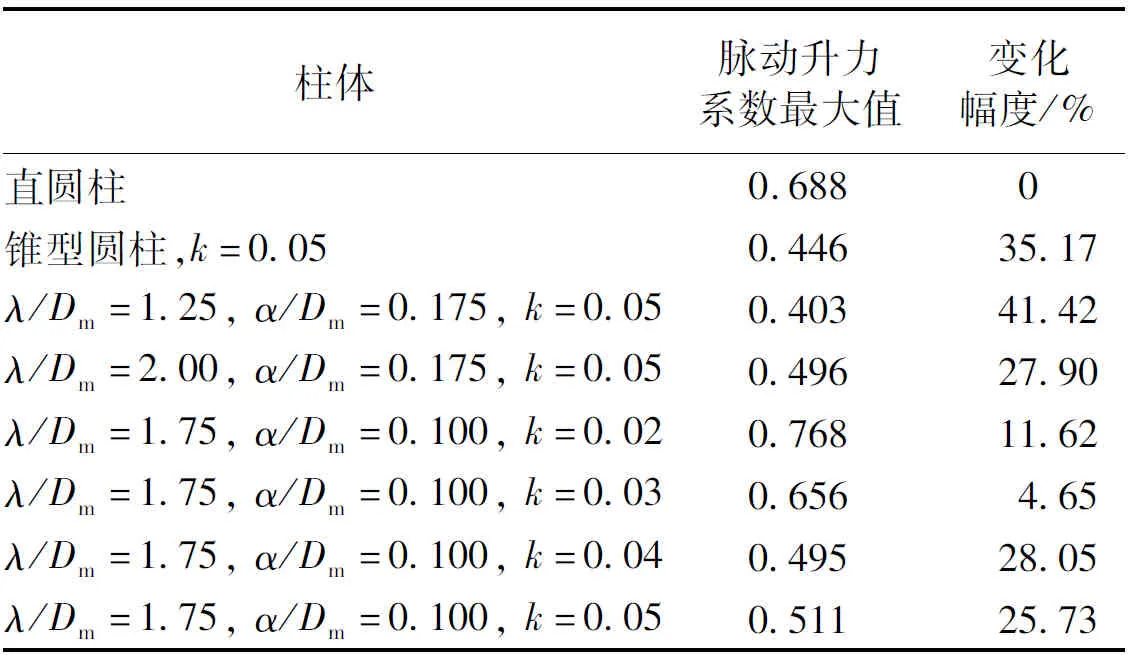
表2 脉动升力系数最大值变化情况
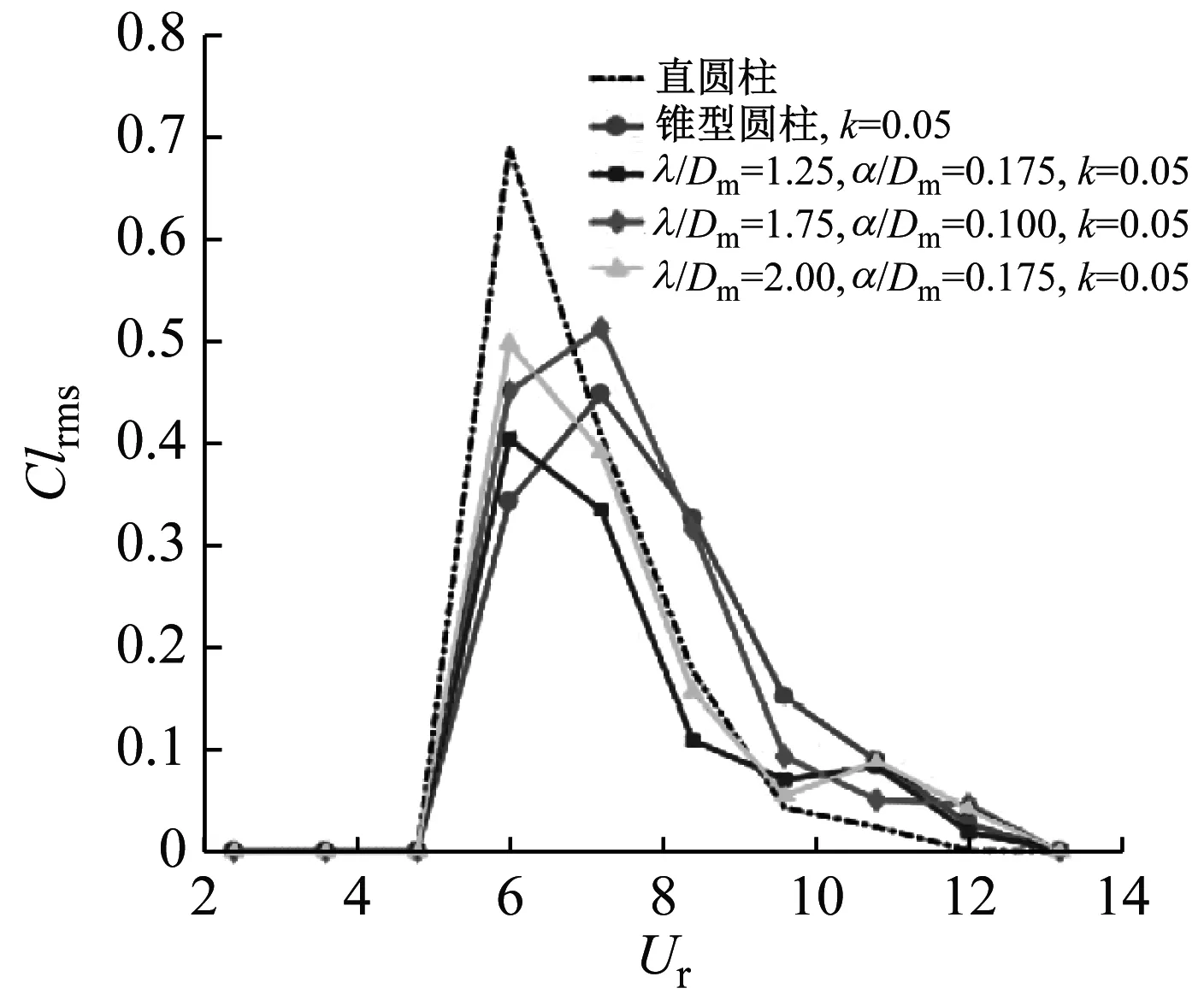
(a)
2.3 相位转化以及流场分析
斜率k=0.05的锥型圆柱和波长比λ/Dm=1.75、波幅比α/Dm=0.10、斜率k=0.05的波浪锥型圆柱在折合流速6.0~12.0的条件下,升力系数与位移的时程图,如图11、图12所示。由图11、图12可知:当折合流速Ur=6.0、7.2和8.4时,锥型圆柱和波浪锥型圆柱的升力系数Cl和振动位移Y/Dm都呈现出“同相位”的特征,且随着折合流速的增大,振动位移不断增大,涡激振动处于锁频区间的开始位置;当折合流速Ur=9.6时,锥型圆柱和波浪锥型圆柱的升力系数与位移的时程图与折合流速Ur<9.6时一样,呈现出“同相位”的特征,但是除此之外,升力系数还呈现出“拍”的特征;当折合流速Ur=10.8时,锥型圆柱的升力系数与位移呈现出“同相位”的特征,同时也呈现出“拍”的特征,结合锥型圆柱的最大振幅比的变化图(见图6)可以得出,这是造成锥型圆柱在锁频区间内最大振幅比一直保持很大振幅的原因,而此时波浪锥型圆柱的升力系数与位移时程图的特征与锥型圆柱却不同,波浪锥型圆柱的升力系数与位移出现“同相位”与“反相位”交替出现的特征,即在一个周期内出现两个峰值;当折合流速Ur=12.0时,锥型圆柱和波浪锥型圆柱的升力系数和位移均呈现出“反相位”特征,此时涡激振动开始退出锁频区间,振动位移也开始减小。
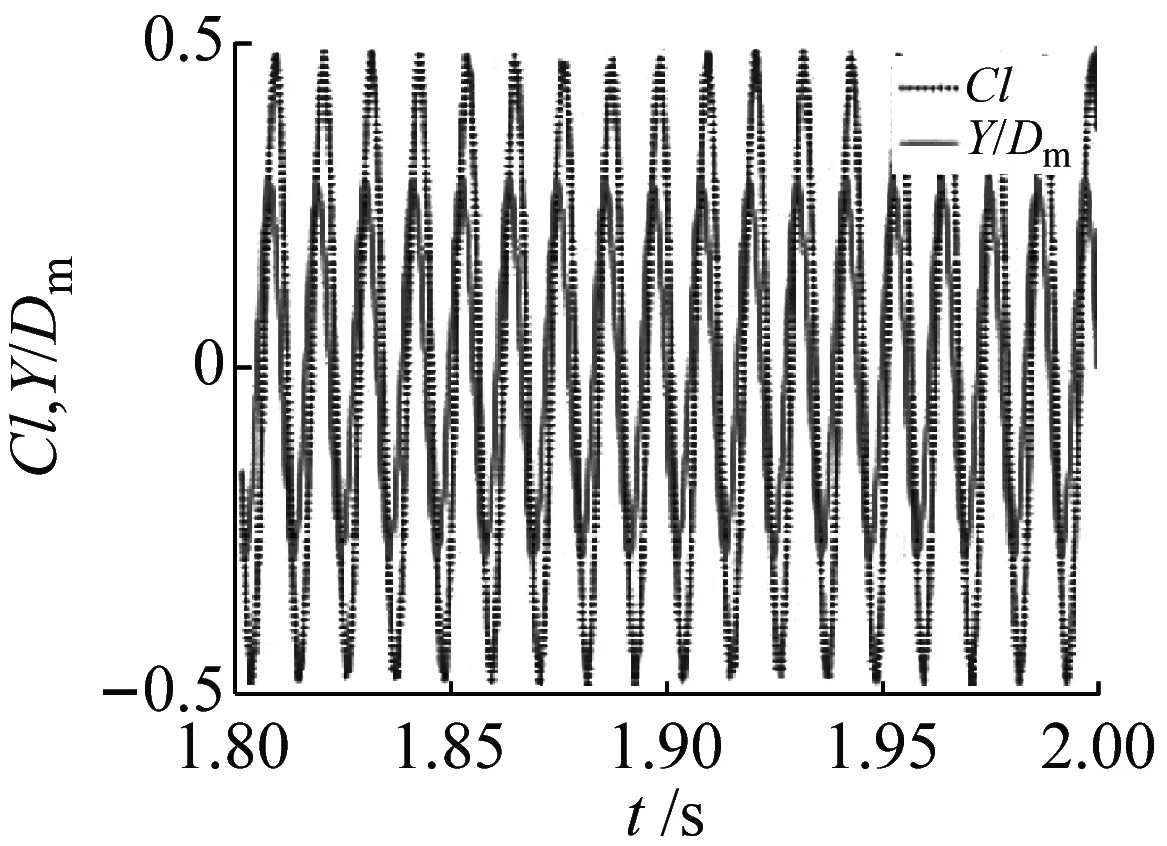
(a) Ur=6.0

(a) Ur=6.0
由于当波浪锥型圆柱进行涡激振动时,折合流速对柱体的流动结构以及涡脱状态影响非常大,从图6可知,波浪锥型圆柱在锁频区间内和在锁频区间外的受力和位移差别是非常大的,而柱体的振动位移又影响着流场的结构。因此本节根据图6的研究结果,选取斜率k=0.05的锥型圆柱和波长比λ/Dm=1.75、波幅比α/Dm=0.10、斜率k=0.05的波浪锥型圆柱为对象,详细分析在不同折合流速内流场的分布情况,在展向方面中间Z截面(Z=0.5H)的涡量图,如图13、图14所示。
由图13、图14可知,当折合流速Ur<6.0时,锥型圆柱和波浪锥型圆柱尾流出现两个很长的剪切层,没有明显涡脱产生。结合图6、图10的结果分析,此时锥型圆柱和波浪锥型圆柱的最大振幅比、脉动升力系数都基本为0,可以得出这种流动结构使柱体保持稳定状态。当6.0≤Ur≤8.4时,锥型圆柱和波浪锥型圆柱脉动升力系数和最大振幅比迅速增大,尾流出现“2S”模式涡脱,即两个大小相同、方向相反的涡交错脱落。当折合流速Ur=9.6和10.8时,锥型圆柱尾流涡脱出现“2P”模式,即两个涡的能量大小不相等、旋转方向相反;并且随着涡脱向下游发展,显现出“2C”模式的迹象,即柱体两侧各出现一对旋转方向相同的涡,但是柱体两侧涡对的旋转方向相反。这意味此时锥型圆柱的涡脱模式有可能实现由“2P”到“2C”的模式转变。此时对于波浪锥型圆柱,涡脱模式依旧是“2S”模式,但是和6.0≤Ur≤8.4时波浪锥型圆柱的涡脱相比,尾流的脱落涡的长度更长。当折合流速Ur=12.0时,锥型圆柱的涡脱又重新出现“2S”模式,但是涡脱的长度与之前相比更长更扁,向着层流的方向发展。当折合流速Ur=13.2时,锥型圆柱和波浪锥型圆柱的流动结构与折合流速Ur<6.0时一致,尾流出现两个很长的剪切层,流动状态重新趋于稳定,此时锥型圆柱和波浪锥型圆柱退出锁频区间,最大振幅比和脉动升力系数急剧减小至0附近。

(a) Ur=2.4
3 结 论
本文选取了两个系列的波浪锥型圆柱,分别是波长比λ/Dm=1.75、波幅比α/Dm=0.10、不同斜率(k=0.02、0.03、0.04和0.05)的波浪锥型圆柱和斜率k=0.05、不同波长比(λ/Dm=1.25、1.75和2.00)、不同波幅比(α/Dm=0.10和0.175)的波浪锥型圆柱,加入直圆柱和斜率k=0.05的锥型圆柱作对比,探究不同折合流速(Ur=2.4~13.2)对各个波浪锥型圆柱涡激振动响应特性的影响,分析波浪锥型圆柱的振动响应特性、升阻力特性以及流动结构,主要得出以下结论:
(1) 直圆柱和锥型圆柱以及各个参数的波浪锥型圆柱的锁频区间基本一致,但是各个参数的波浪锥型圆柱最大振幅比各不相同,其中斜率k=0.05的锥型圆柱和波长比λ/Dm=1.75、波幅比α/Dm=0.10、斜率k=0.05的波浪锥型圆柱最大振幅比较大,不同折合流速下其最大振幅比的最大值和直圆柱相比分别增长26.4%和12.6%。
(2) 在锁频区间内(4.8
