不同迎流攻角下正三角柱流致振动数值模拟研究
2022-02-22卫昱含及春宁陈威霖
卫昱含, 及春宁, 许 栋, 陈威霖
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
流体流经柱体时会在柱体后方产生旋涡,进而诱发柱体产生振动。根据产生机理的不同,流致振动可以分为涡激振动和驰振两种。涡激振动是由脱涡和柱体相互作用引起的振动,因此脱涡与振动具有相同的频率。涡激振动具有自限性,大幅振动仅在一定的流速范围内出现。根据研究参数的不同,对于低质量比层流条件,当柱体的振动频率与脱涡频率一致并且接近柱体在真空中的固有频率时,锁定出现,此时柱体的振幅较大,而超出锁定区间后,柱体的振动将会受到显著抑制。驰振则是由于流动分离和旋涡脱落而产生的流体动力负阻尼分量引起的振动。驰振不具有自限性,表现为一种低频高振幅响应。随着流速的增加,响应振幅单调增大。一方面,流致振动常常会引起像海洋立管、海底输油管道、桥梁等结构疲劳破坏,从而造成巨大的经济损失。另一方面,流致振动也可用于海流能的开发利用[1-2]。长期以来,学者们对流致振动响应的研究多集中在圆柱上,并且得到了很多重要的结论[3-7],然而驰振多发生于正方形、矩形、三角形等复杂不规则的非流线型截面结构中[8-10]。由于三角柱截面具有尖角、固定的流体分离点以及分离尾流中的后体,使得其不再像圆柱具有绝对对称性,同时也表现出了更多的振动特性。防风屏障和桥面都是容易发生驰振的细长结构,这些结构中都具有三角形截面,因此研究三角柱的流致振动机理具有重要的科学和现实意义。
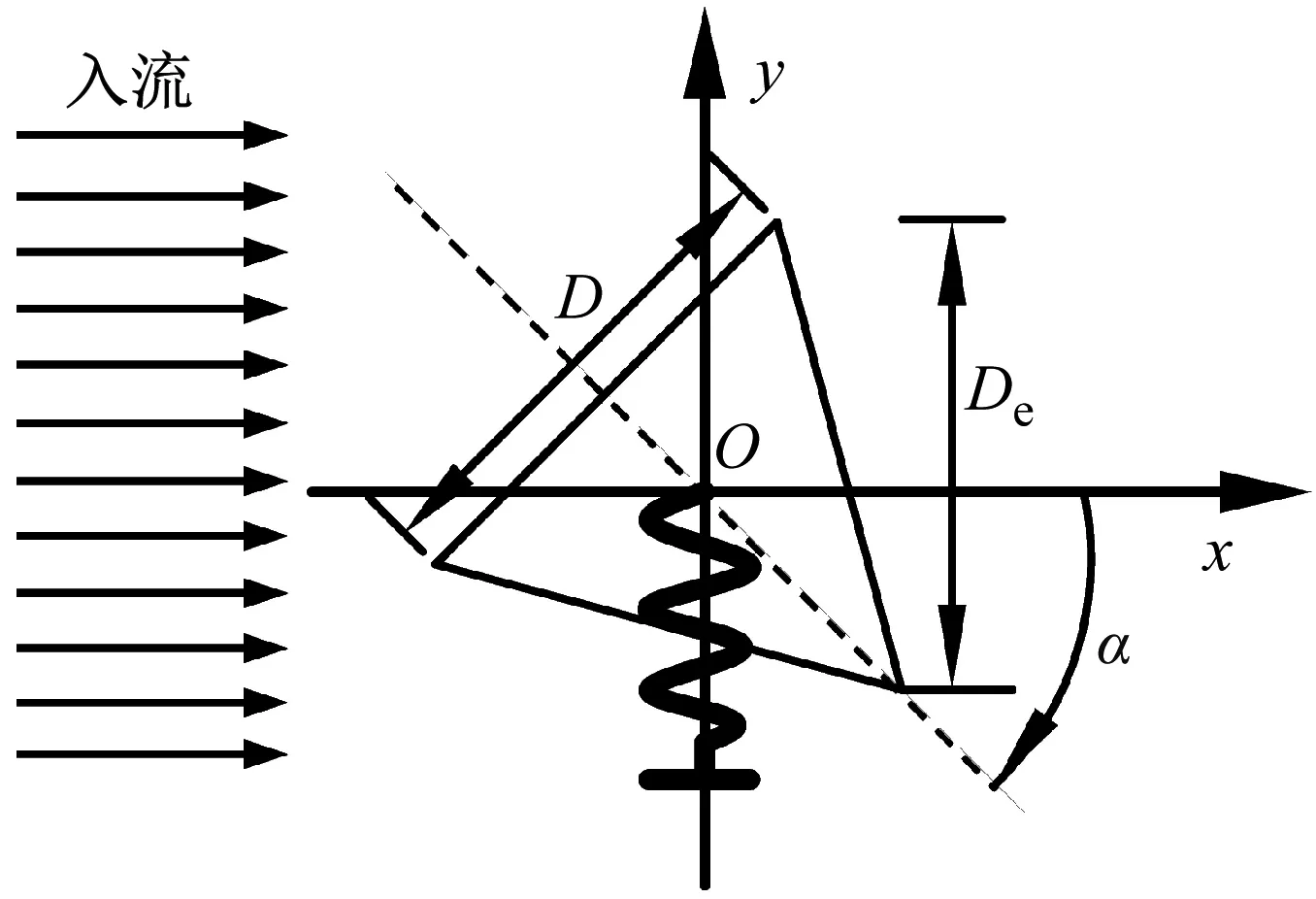
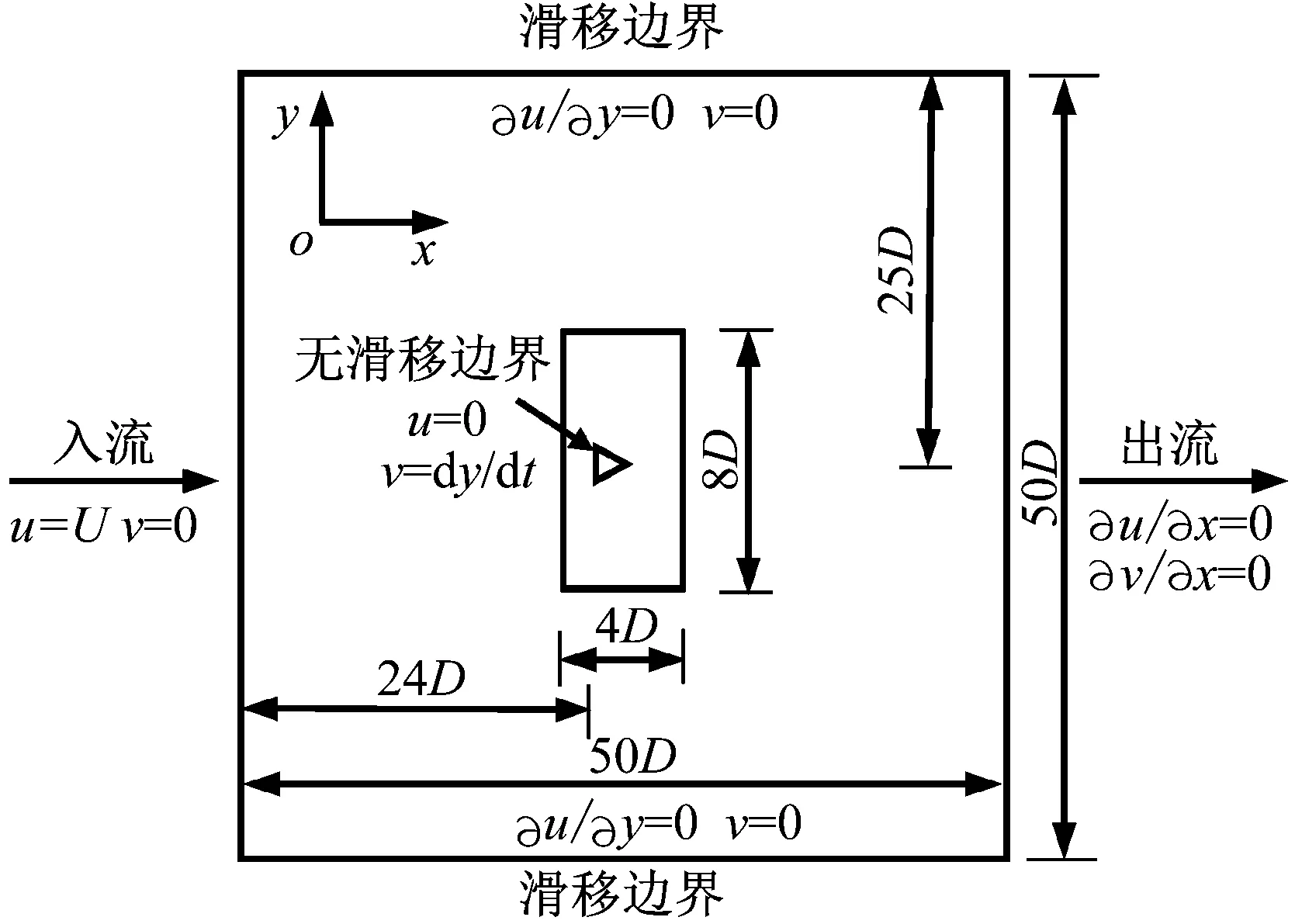
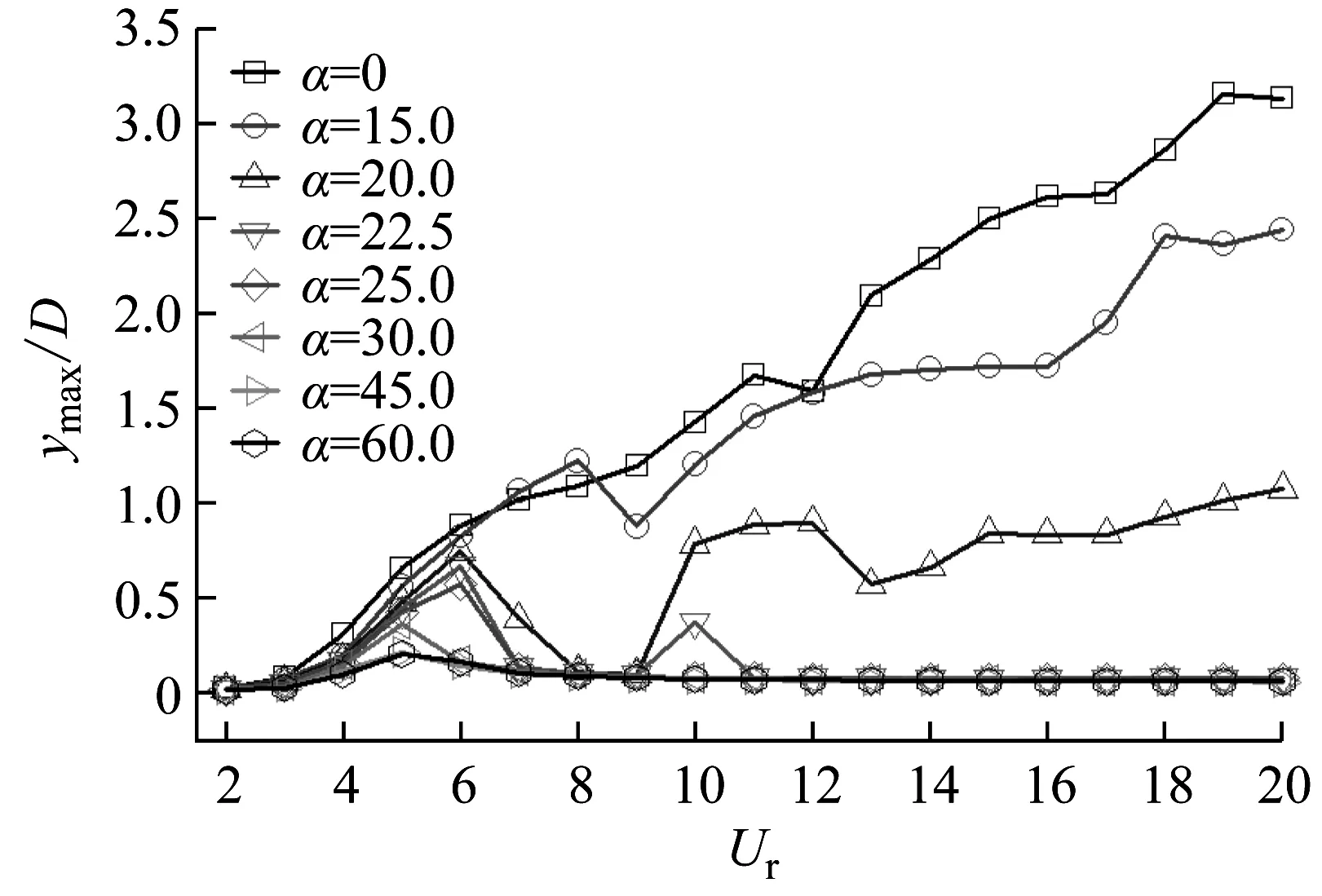
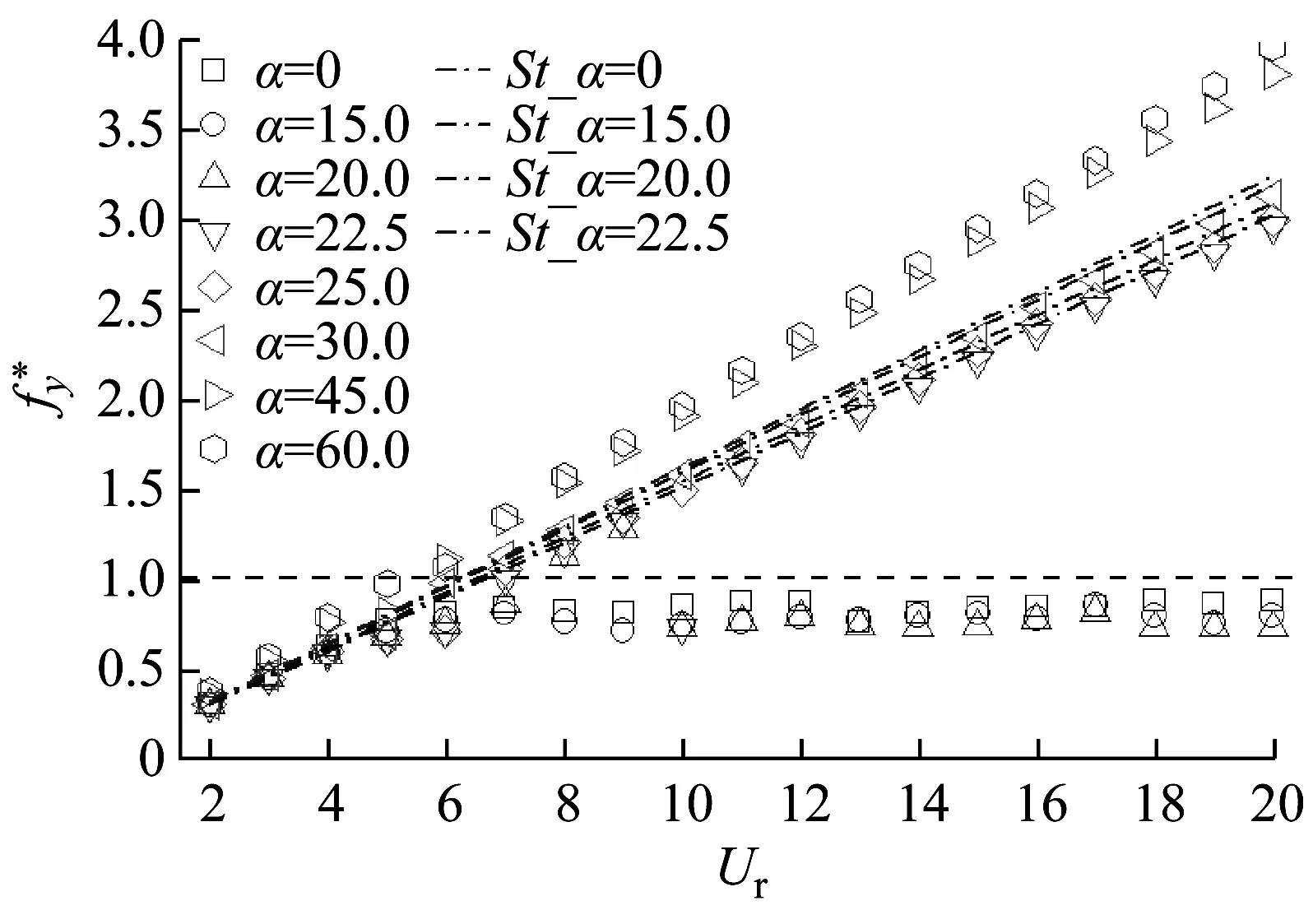
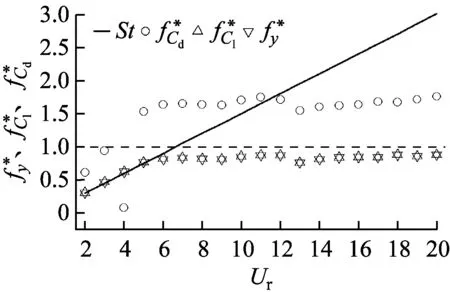
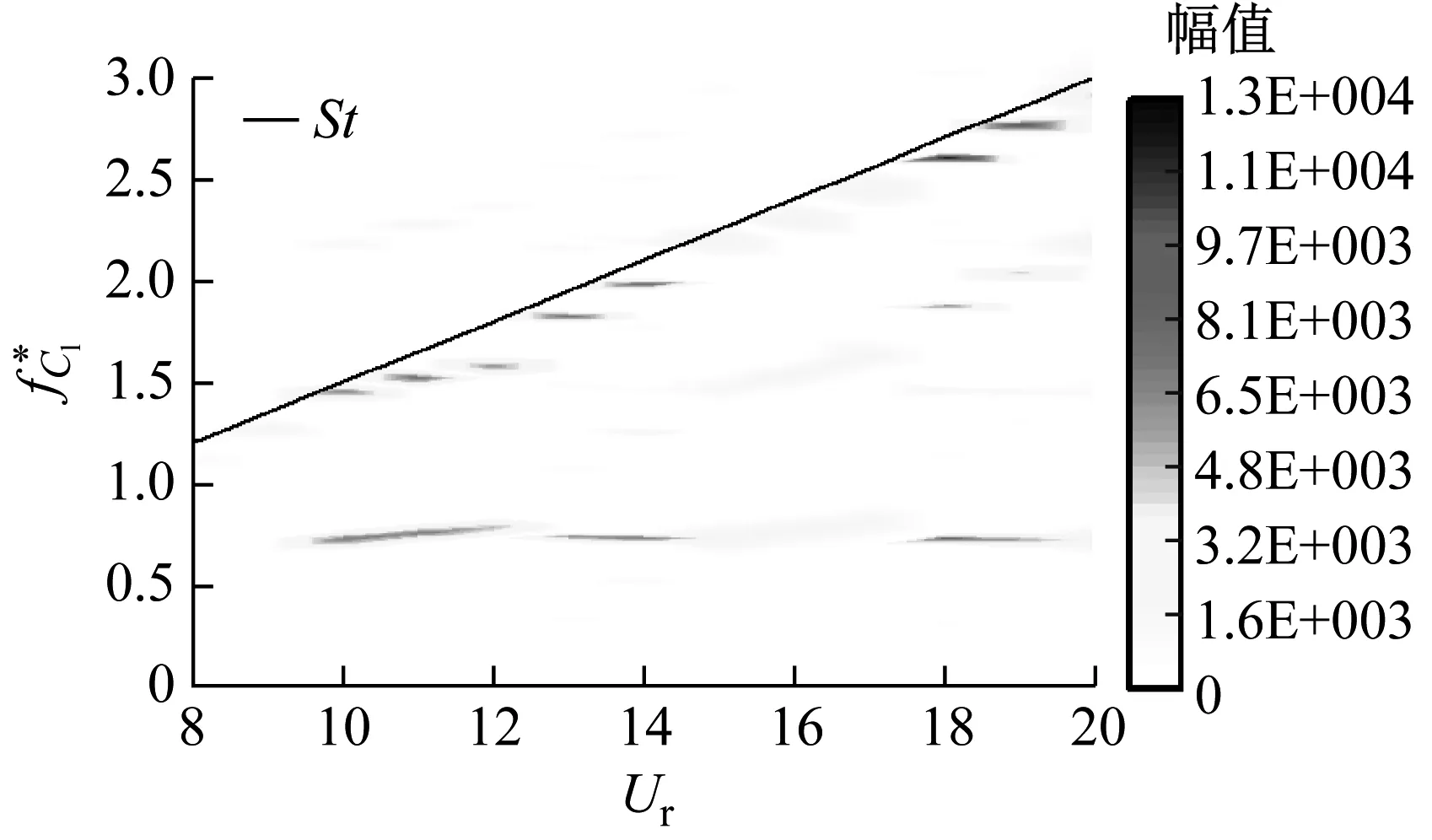
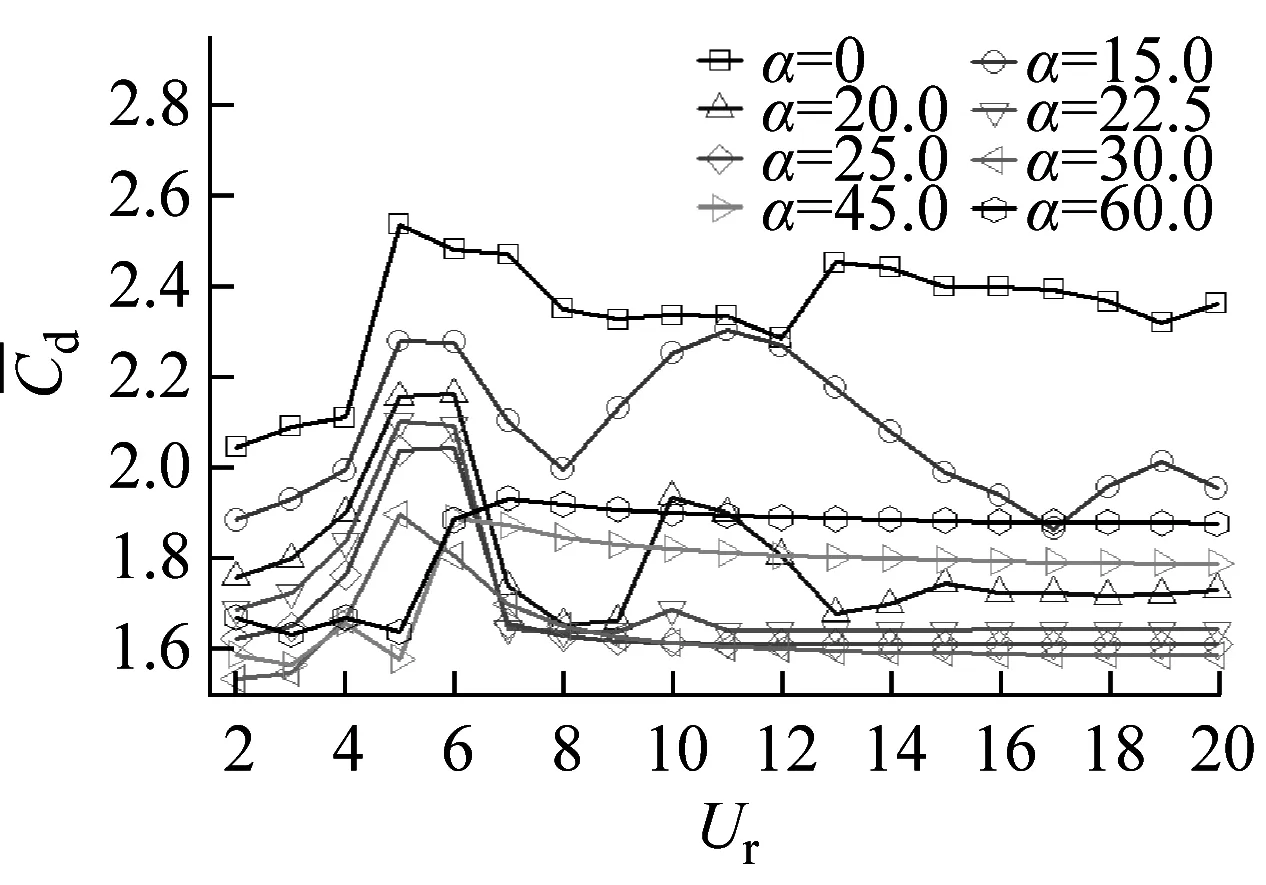
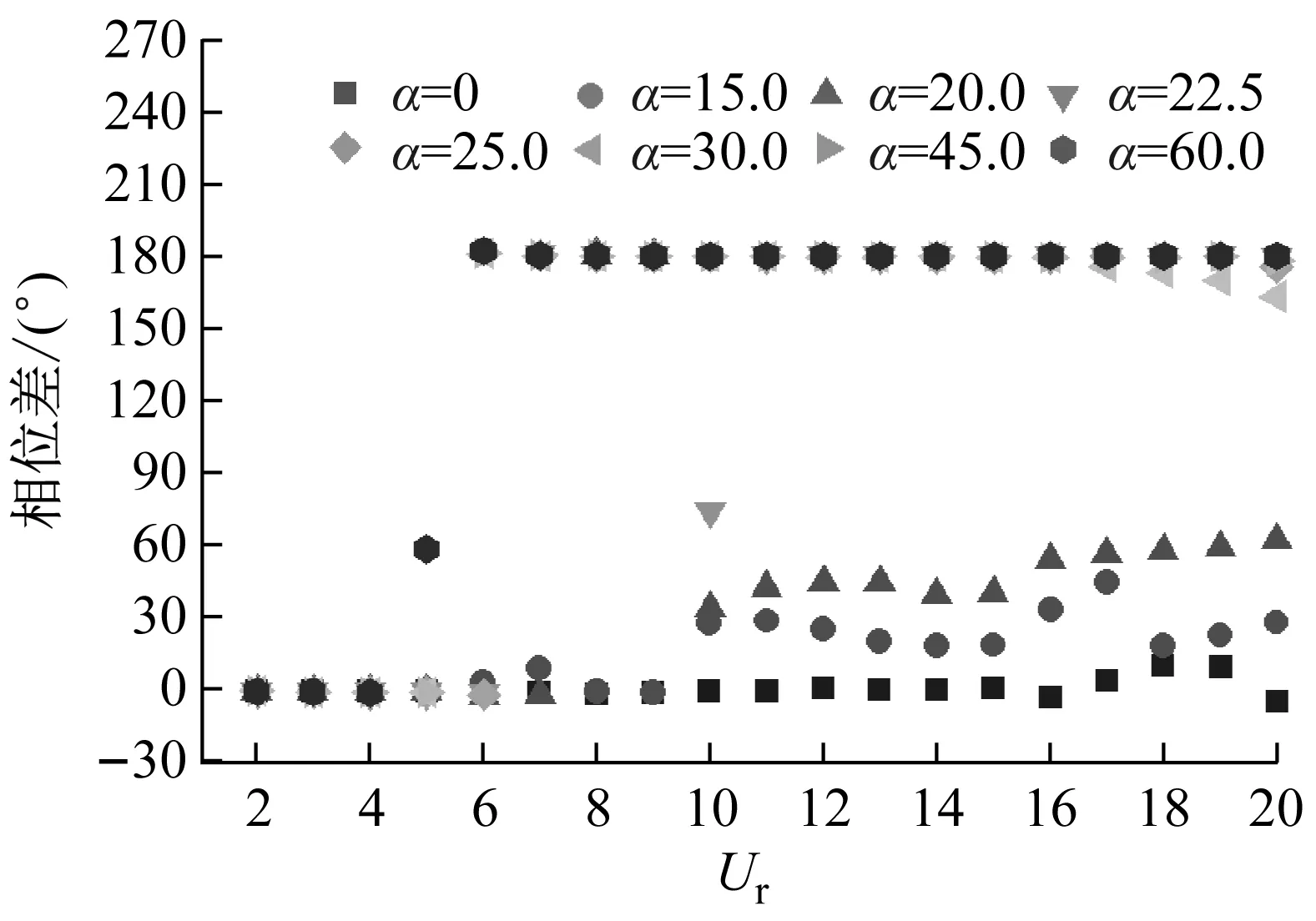
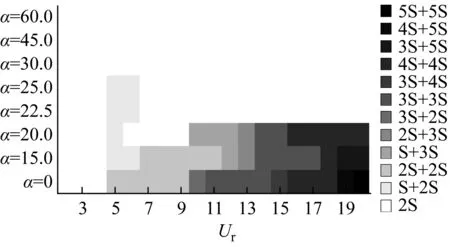
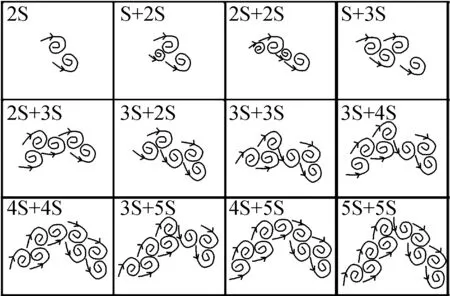
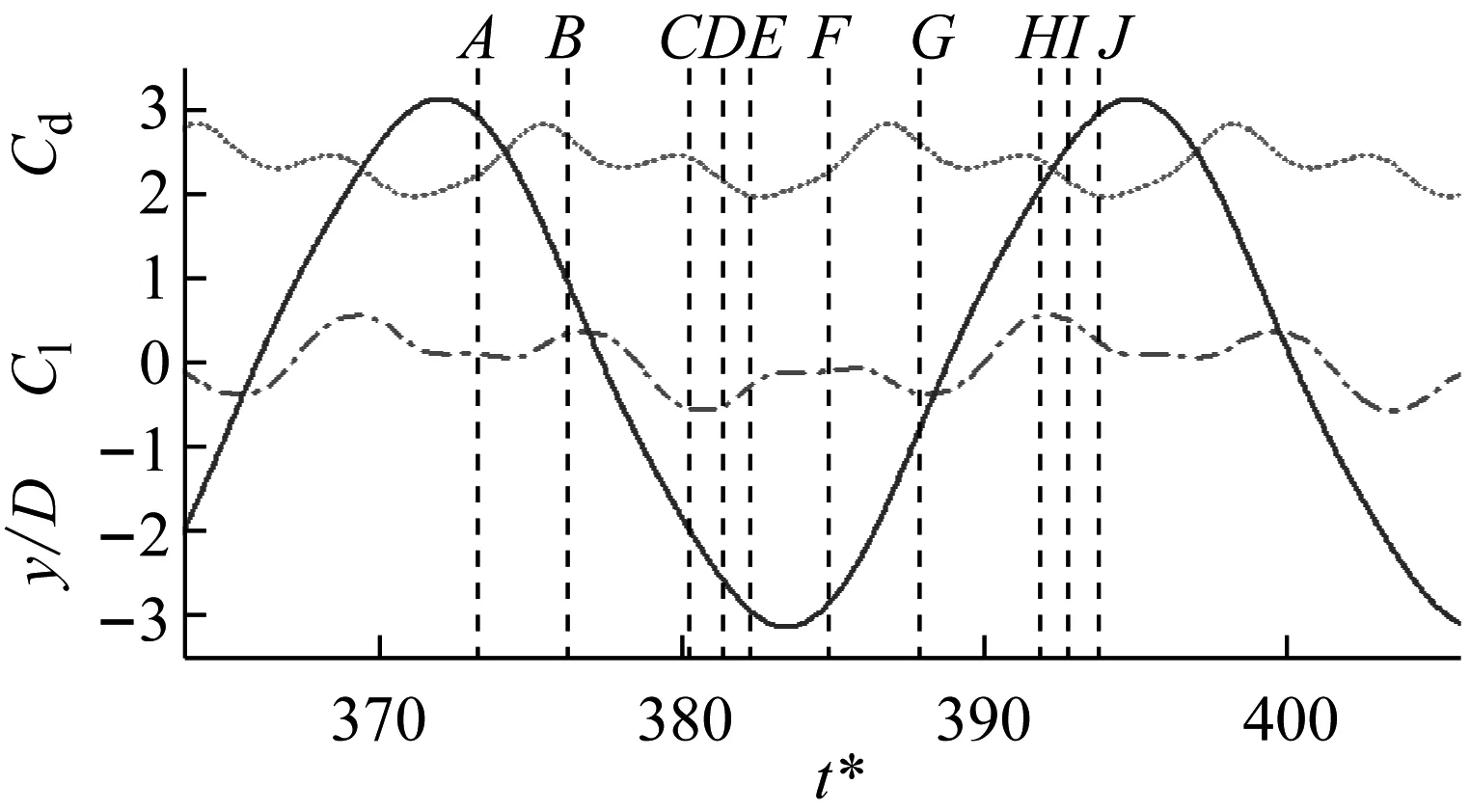
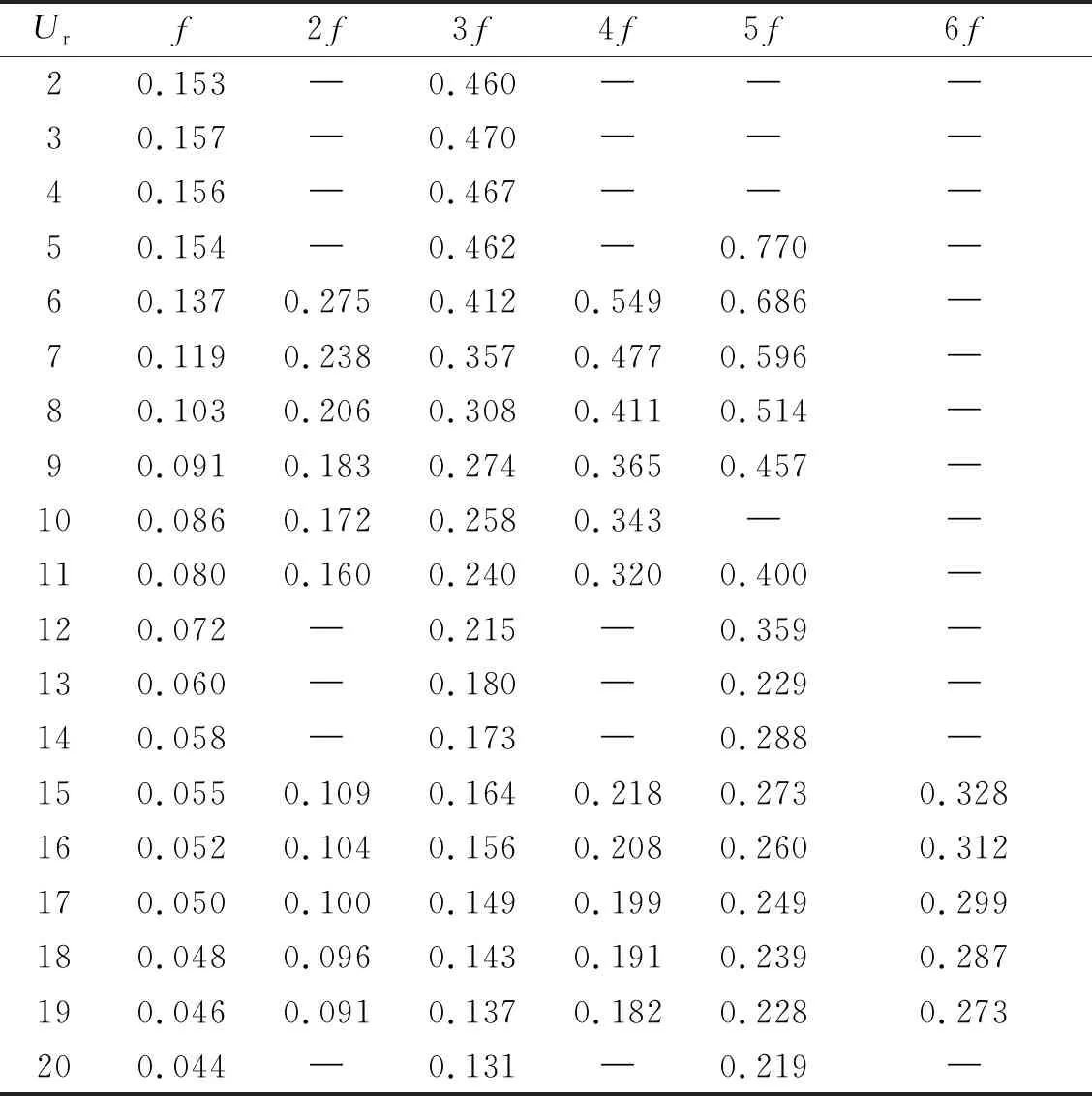
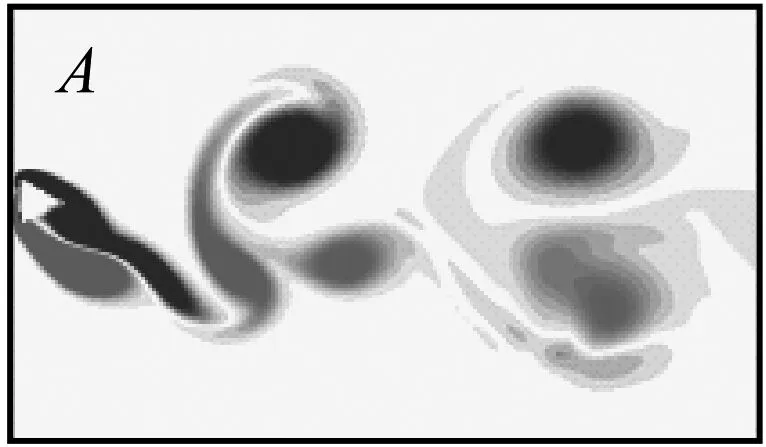
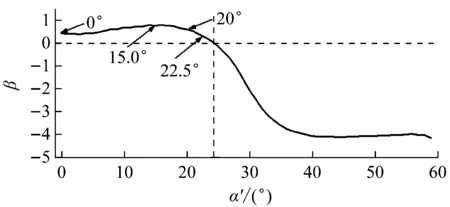
Wang等[11]对不同迎流攻角下Re=100和m*=2时三角柱流致振动的研究发现α=60°(顶点迎流)、30°时三角柱发生了与圆柱类似的涡激振动响应模式,α=0°时出现了典型的低频高振幅驰振响应。此外,α=0°、30°时观察到2S尾涡模式,α=60°出现了P+S和2P尾涡模式。类似地,Zhang等[12]在等边三角柱(边垂直迎流)的流致振动试验中也观察到涡振和驰振响应模式,并且在涡振到驰振的过渡区域发现了涡振-驰振转变分支,该分支发生在7.8 结合以上综述可以发现,目前对三角柱流致振动的系统研究仍比较少。本文对不同迎流攻角下正三角柱的流致振动进行数值模拟研究并对以下3个关键问题给出解答。①不同迎流攻角下三角柱振动响应和频率随折合流速将出现怎样的变化。②为什么升力系数偶次谐波分量是对称工况下结构平衡位置偏移不为零的原因。③准稳定性理论能否准确预测三角柱发生驰振响应的迎流攻角范围。 流致振动的数值模拟方法采用浸入边界法[23],其控制方程如下 (1) ∇·u=0 (2) 式中:u为速度;t为时间;p为压强;v为运动黏滞系数;∇为梯度算子;f为附加体积力矢量,代表流固耦合边界条件。 对以上控制方程采用二阶精度的Admas-Bashforth时间格式进行离散,得到如下形式 (3) ∇·un+1=0 (4) 式中:h=∇·(-uu+ν(∇u+∇uT))由对流项与扩散项组成;上标T为矩阵转置,附加体积力表示为 (5) 对于传统浸入边界法施加边界条件精度不高的问题,Ji等提出了基于嵌入式迭代的浸入边界法,将浸入边界法嵌入到压强泊松方程的迭代求解中,利用压强的中间解比初始值更接近真实值的特点,迭代修正附加体积力,在不显著增加计算耗时的前提下,提高了整个算法的求解精度。 仅做横流向振动的弹性支撑刚性三角柱的运动方程如下 (6) 式中:m为三角柱质量;c为系统结构阻尼;k为弹簧刚度系数;Fy为三角柱受到的横向流体力。方程采用标准的Newmark-β法求解。 对不同迎流攻角下正三角柱的流致振动展开了数值模拟研究,其中三角柱仅在横流向自由振动。三角柱的边长为D=1,雷诺数为Re=UDe/v=100,De为三角柱迎流有效长度,质量比为m*=m/mf=5,m为柱体的质量,mf为柱体排开水的质量,迎流攻角为α=0°~60°,以其中一尖角迎流的情况为α=60°,如图1所示,折合流速为Ur=U/fnD=2~20,fn为柱体的自然频率。此外,为激发大振幅振动结构阻尼比c取为零。 图1 三角柱的布置示意图 如图2所示,采用的计算域为50D×50D,在柱体周围采用局部加密网格,网格大小为Δx=Δy=1/64D,其中加密区大小为4D×8D。柱体中心放置在距离入流边界24D,距离上边界25D的位置。边界条件设置如下:入口边界条件为均匀来流,u=U,v=0;出口边界条件为Newmann型边界,∂u/∂x=0,∂v/∂x=0;上下边界为滑移边界,∂u/∂y=0,v=0;柱体表面为无滑移边界,u=0,v=dy/dt。 图2 计算域与边界条件设置 表1 雷诺数Re=100条件下三角柱绕流结果对比 3.1.1 横向振幅 图3 不同迎流攻角下三角柱的振动振幅随折合流速变化情况 图4 不同迎流攻角下三角柱的振动频率随折合流速变化情况 3.1.2 振动频率 (a) α=0° 图6 α=20°时升力和振幅的频率谱随折合流速的变化 3.1.3 水动力系数 (a) 阻力均值 3.1.4 升力与位移的相位差 图8 不同迎流攻角下三角柱的升力与位移的相位差随折合流速变化情况 3.1.5 尾涡模式 图9给出了不同折合流速和迎流攻角下三角柱的尾涡模式情况。按照柱体向下振动脱涡个数(n)+向上振动脱涡个数(m)的方式来命名脱涡模式(nS+mS)。由于三角柱出现了涡振-驰振联合和涡振-驰振分离的响应,所以在研究范围内出现了多种形式的尾涡模式。驰振分支内三角柱在一个振动周期内脱涡个数随着折合流速的增加而增加。整体而言,振幅越大,脱涡个数越多。特别地,对于涡振响应(α=25°~60°),尾涡模式均为2S模式,仅在α=25°、Ur=5~6内出现了S+2S脱涡模式。图10为不同尾涡模式的示意图。2S模式中两个单独的涡分别从三角柱两边脱落,S+2S模式中三角柱交替脱落一个单涡和一个涡对,与自激振动圆柱的P+S尾涡模式相似,2S+2S模式中三角柱从两侧交替脱落两个涡对,与自激振动圆柱的2P尾涡模式相似。一个振动周期内,三角柱脱落更多数量的涡(n>2或m>2)仅在驰振模式下出现。 图9 三角柱的尾涡模式 图10 尾涡模式的示意图 以α=0°和Ur=20时三角柱的尾涡模式5S+5S对驰振分支的尾流情况进行说明。图11给出了该模式的涡量等值线时程变化情况。从涡量等值线图来看,三角柱在向下过程中脱落2个逆时针涡(2、4)和3个顺时针涡(1、3、5),升力均值为负,而向上过程中对应脱落2个顺时针涡(2′、4′)和3个逆时针涡(1′、3′、5′),升力均值为正。可以看出,在驰振分支内,振动周期明显大于脱涡周期,与Zhao等对方柱驰振的研究结果一致。 (a) 图12 不同折合流速下三角柱的平衡位置偏移随折合流速变化情况 表2 α=0°时不同折合流速下升力的频率 为了进一步说明升力偶次谐波分量出现的原因,分别选取了平衡位置偏移为零和非零的两个折合流速Ur=8、13进行对比,如图12所示。对比涡量等值线图(图13(a)和图13(c),A:三角柱位于振动波峰,B:三角柱位于振动波谷)可以发现:Ur=8工况中,三角柱位于波峰和波谷时的涡量不对称,且逆时针涡占主导,所以平衡位置向上偏移;而Ur=13工况中,三角柱位于波峰和波谷时的涡量对称,所以未发生平衡位置偏移,这说明了脱涡在平衡位置偏移中起到了重要作用。 (a) Ur=8时三角柱的涡量等值线图 根据Govardhan等[34]对升力的分解方法将升力分为涡力分量和势能力分量 Ctotal(t)=Cvortex(t)+Cpotential(t) (7) Cpotential(t)=2π3(y(t)/D)/(Ur/f*)2 (8) 式中:Ctotal为总的升力系数;Cvortex为涡力分量系数,Cpotential为势能力分量系数;f*为无量纲升力频率。 如图13(b)和图13(d)所示,由Ur=8、13时升力的分解结果,可以看到势能力分量在三角柱向上和向下运动过程中均对称,而Ur=8时涡力分量在三角柱向上和向下运动过程中出现了不对称现象,这进一步佐证了平衡位置偏移不为零是由脱涡引起的。 如图3所示,三角柱在α=0°~22.5°时出现了驰振现象,本文通过准稳定性分析方法研究Re=100时三角柱发生驰振的迎流攻角范围。该方法假设流体力与柱体振动速度同相,将作用在运动物体上的瞬时力替换为相同迎流攻角(考虑来流速度和物体速度)的物体所受的静态力[35]。 Cl=Cl|α′=0+[(∂Cl/∂α′)|α′=0]α′+… (9) (10) (11) 式中:ζ为阻尼比;ωn为角频率。方括号中的值为0是驰振响应发生的临界条件[37],由此可以推得临界流速Uc=4mωnζ/[ρD(∂Cl/∂α′)],对其进行无量纲化得到临界折合流速 (12) 当Ur>Ucr时,驰振开始发生。由于本文数值模拟的c=0,即ζ=0,所以α=0°时,驰振发生于Ur=0。对于迎流不对称的工况,由于升力均值不为0,即Cl|α′=0≠0,所以发生驰振时Ur>0,这一点与图3结果是一致的。 根据Den Hartog[38]提出的横向驰振判据,对于无阻尼系统将在下述条件成立时发生驰振失稳现象 (13) 图14为Re=100条件下,通过三角柱绕流的数值模拟结果得到的β随α′的变化趋势。其中,初始角度α0=0°。可以看出:当α′<24.4°时,β>0,所以在α<24.4°内三角柱发生驰振响应。对比3.1.1节对横流向振动振幅的分析,三角柱确实在α≤22.5°的攻角范围内出现了驰振分支,特别是当α=22.5°时,仅在Ur=10处出现了一个小的驰振分支。整体来看,准稳定性理论对预测驰振发生的攻角范围具有较好的效果。 图14 三角柱的β随α′的变化趋势图 应用嵌入式迭代浸入边界法研究了层流条件下不同迎流攻角时正三角柱的流致振动现象,分析了各工况下三角柱的横流向振幅、振动频率、水动力系数、升力与位移的相位差以及尾涡模式随迎流攻角和折合流速变化的情况,最后检验了准稳态分析对驰振现象的预测可靠性。 研究结果表明: (1) 当α=0°~15°时,三角柱的振动为涡振-驰振联合模式;当α=20.0°~22.5°时,振动为涡振-驰振分离模式;当α=25°~60°时,振动为涡振模式。由于三角柱的分离点固定,振动频率随着折合流速线性增加,涡振响应表现出非锁定特性。 (2) 随着迎流攻角和折合流速的变化,三角柱出现了多种尾涡模式。对于发生涡振的迎流攻角,其尾涡模式表现为和低质量阻尼比时圆柱类似的2S模式。而对于具有驰振分支的迎流角度,其脱涡个数随着振幅的增大而增大。 (3) 当α=0°时三角柱出现了平衡位置偏移不为零的现象,通过快速傅里叶变换对升力进行频谱分析,发现该现象的出现是因为升力存在偶次谐波分量,而偶次谐波分量的出现与脱涡相关。 (4) 准稳定分析预测的三角柱发生驰振的迎流攻角范围与数值模拟结果一致,说明准稳态分析可以准确预测驰振不稳定性。1 数值模拟方法
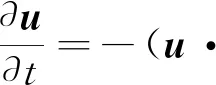
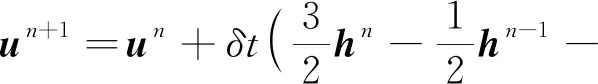
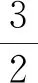
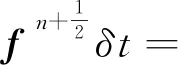
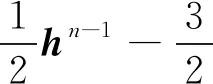
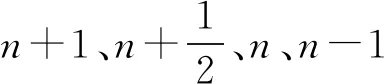
2 数值模型及其验证
2.1 问题描述
2.2 模型设置
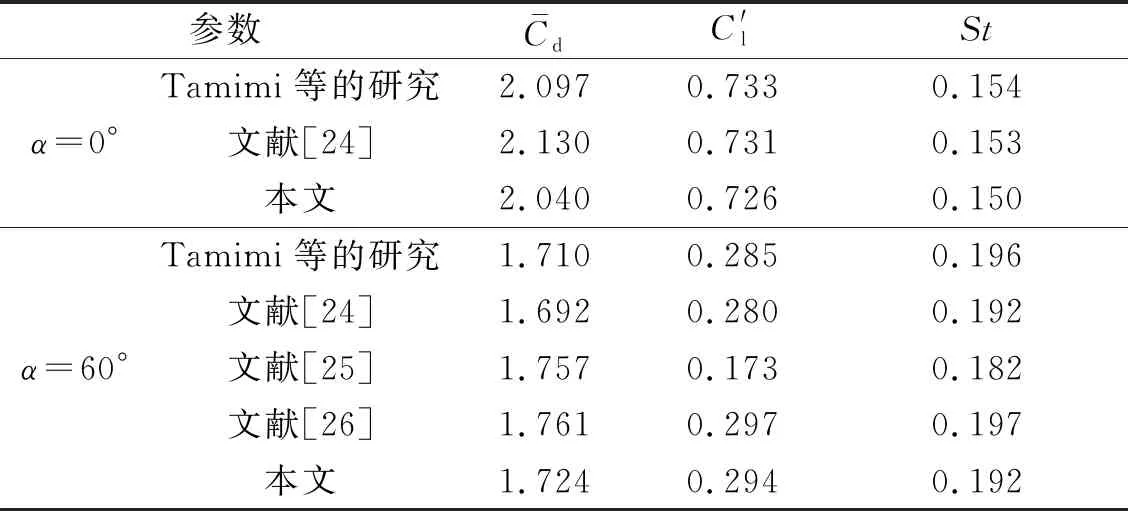
2.3 方法验证
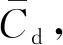
3 结果和讨论
3.1 振动响应

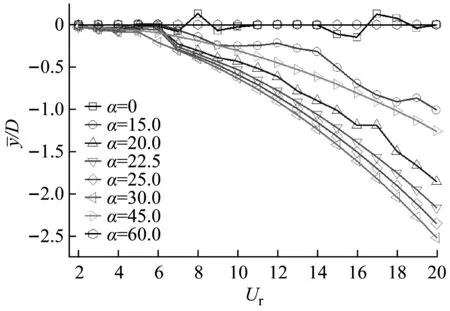
3.2 平衡位置偏移
3.3 准稳态分析

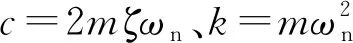
4 结 论
