基于主余震序列的高拱坝极限抗震能力损失研究
2022-02-22金爱云王进廷潘坚文
金爱云, 王进廷, 潘坚文
(清华大学 水沙科学与水利水电工程国家重点实验室, 北京 100084)
我国西南地区是许多大江大河的发源地,高山峻岭密布,河流有着极大的天然落差,高混凝土坝多修建于此。然而西南地区也是我国的地震重灾区,这些高坝的库容都在几十甚至上百亿立方米,一旦在地震作用下发生溃决,将引发不可估量的生命财产损失和生态灾难。因此,大坝在地震作用下的安全性问题成为大坝设计的重中之重。众所周知,地震一般由前震,主震和余震构成。统计表明,约90%的强主震伴随着强余震的发生[1],主震强度越高则伴随的余震强度越大[2]。近年来一些大震如2008年汶川地震、2013年芦山地震和2015年尼泊尔Gorkha地震等,均伴随发生了大量强余震[3-5]。大量震害资料表明强余震也具有较大的破坏能力。当主震导致结构损伤后,在强余震或多次余震的作用下,结构的损伤将会进一步累积,并可能最终导致结构倒塌。因此,有必要在目前高坝的抗震设计中进一步考虑余震的影响。
国内外已有一些学者对主余震序列作用下结构的动力响应规律进行了研究。杨佑发等[6]研究了余震对掉层结构易损性分析结果的影响,结果表明余震会提高掉层结构的超越概率。韩建平等[7]考虑了不同的主余震序列构造方法,研究了余震方向性和余震次数的影响。柳春光等[8]将两次地震首尾相连构建主余震序列,研究了桥梁结构在两次地震作用下的动力响应,表明连续两次地震作用下结构的地震危险性增加。Jalayer等[9]以抗弯钢架为例,考虑余震发生的时间依赖性,研究了余震引起的损伤累积效应和对极限状态超越概率的影响。Wang等[10]以某32层框架芯管结构为例,研究了主余震序列作用下高层结构的地震脆弱性,结果表明随着主震引起的破坏状态变得越来越严重,主震下受损的建筑物对于余震激发变得越来越脆弱,并且对余震强度越来越敏感。Wen等[11]以钢筋混凝土框架结构为研究对象,提出了在主余震序列作用下研究结构脆弱性的框架。在高坝领域,熊瑜等[12]将数值模拟与模型试验结合,研究了复杂地基情况下主余震序列对重力坝稳定性的影响,结果表明坝体变形相对单独主震情况下大幅增加。翟亚飞等[13]结合NGA地震动衰减模型构建主余震序列,结果表明在主震导致坝体受损的情况下余震能引起明显的残余变形。王高辉等[14]研究了主余震序列作用下重力坝的损伤累积破坏效应,表明余震自身地震特征对坝体位移的重要影响。Zhang等[15]建立了局部损伤指标和整体损伤指标,对比了实测主余震序列和人工主余震序列,表明实测主余震序列能引起更大的损伤累积。Alliar等[16]研究了在考虑余震和排水系统效率降低的情况下重力坝的地震安全性。Pang 等[17-18]以某200 m高的混凝土面板堆石坝(concrete face rockfill dam,CFRD)为例,采用弹塑性分析的方法研究了主余震序列对坝体抗震性能的影响,结果表明CFRD在经历余震时会遭受额外的地震损伤,且脆弱性显著增加。
目前,高坝领域对主余震序列的研究尚缺乏对拱坝的研究成果。此外,已有的研究着重于分析余震是否会带来影响,表明余震可能引起结构危险性增加,然而缺乏对余震作用下结构的破坏行为进行分析,也并未量化主震受损带来的影响。从工程角度而言,人们更关心的是主震受损的结构还能承受多大强度的余震,也即极限抗震能力的变化程度,以便对后续修复工作进行指导。对该问题的研究需要在不同主震受损状态下进行多次余震试算直至结构失效,同时应该考虑地震的不确定性。因此,为兼顾计算成本与计算结果的合理性,本文基于耐震时程法(endurance time analysis, ETA)[19]构建主震-ETA余震序列以进行高拱坝动力分析,并与单独主震的情况进行比较,以量化主震受损对高拱坝极限抗震能力的影响,并给出不同主震强度下高拱坝极限抗震能力的变化情况。
1 分析模型
1.1 拱坝-库水-地基有限元模型
选取大岗山混凝土双曲拱坝为分析案例。大岗山拱坝最大坝高210 m,坝顶高程1 135 m,正常蓄水位高程1 130 m。有限元模型如图1所示,由37 120个八结点六面体实体单元和53 817个结点组成。坝体由28条横缝分为29个坝段,横缝采用接触边界模型[21]进行模拟,使用Westergaard附加质量[22]模拟大坝与库水之间的相互作用,采用黏弹性人工边界[23]来模拟半无限地基的辐射阻尼效应。计算中考虑了坝体混凝土的非线性行为,并采用Lee等[24]提出的混凝土塑性损伤本构模型。坝体阻尼采用Rayleigh阻尼,取第一阶和第五阶的阻尼比为5%。坝体混凝土密度2 400 kg/m3,初始弹性模量31.2 GPa,泊松比0.17,抗拉强度ft为3.25 MPa,断裂能Gf为280 N/m,极限拉应变εf为4×10-4。地基弹性模量26.0 GPa,密度2 625 kg/m3,泊松比为0.25。

(a) 坝体-地基有限元模型
1.2 耐震时程法
耐震时程法由Estekanchi等提出,是一种动态的Push-Over方法,通过拟合出满足特定条件的人工地震动开展结构动力分析,其重要特征之一是地震强度随时间持续增长。具体来说,耐震时程法中人工地震动在某时段(0~t)内计算得到的加速度反应谱(本文定义为t时刻对应的加速度反应谱)与该时段的持时t呈线性关系
(1)
式中:T为结构自振周期;t为地震动任意时间点;tR为预先指定的目标时刻;Sa,Tar(T,t)为地震动在t时刻的目标加速度谱;Sa,R(T)为预先指定的tR时刻对应的加速度谱。通过指定tR和Sa,R(T),便能得到任意时刻的目标加速度谱,并以此为目标进行地震动拟合。
耐震时程法中,人工地震动在0~t时段内计算得到的位移反应谱为
(2)
式中,Sd,Tar(T,t)为t时刻的目标速度谱。对某一时刻而言,可以使拟合得到的地震动在一定精度条件下同时满足式(1)和式(2)。然而,耐震时程法在理论上要求式(1)和式(2)对任意时刻都成立,这显然是没有必要,也无法实现的。通常,简化为在某些时刻及一定精度条件下满足式(1)和式(2),此时耐震时程法中的地震拟合实际上是一个无边界的优化问题
Sa,Tar(T,t)]2+αD[Sd(T,t)-
Sd,Tar(T,t)]2}dtdT
(3)
式中:ag为拟合得到的地震动;Sa(T,t)和Sd(T,t)分别为在t时刻基于ag计算得到的加速度谱和位移谱;αD为位移谱的权重系数,根据Estekanchi等的建议,αD越小则加速度反应谱在短周期范围内拟合得越好,因此本文中取αD=0,Tmax和tM分别为拟合中所考虑的最大周期和最长地震持续时间,分别为3 s与30 s。
采用以上步骤所拟合得到的地震动的示意图如图2所示。通过人为控制,可以使耐震时程法中的最大地震强度值(本文用基频对应的谱加速度Sa(T1)表示地震动强度值,T1为基频对应的自振周期。)尽可能大,从而通过一次ETA计算便可以得到结构从完好到破坏的过程中不同地震强度所对应的结构动力响应,相当于一次完整的增量动力分析法(incremental dynamic analysis ,IDA)计算,能显著减少计算工作量。
图2 耐震时程法拟合的地震动示意图
1.3 地震记录
为研究余震作用下高拱坝的破坏行为,量化主震受损对高拱坝极限抗震能力的影响,本文提出将高拱坝极限抗震能力损失程度定义为
(4)
式中:dC为高拱坝震后极限抗震能力的损失程度;Cb为高拱坝完好时的极限抗震能力;Cp为高拱坝震后的极限抗震能力。
需要说明的是,本文中极限抗震能力代表高拱坝破坏时对应的地震强度(破坏强度)。由于地震存在不确定性,则应通过破坏易损性分析[25]求出单独主震情况下高拱坝不同极限抗震能力的概率水平,同时考虑多条主震-ETA余震序列用于计算。因此,本文中根据DL 5073—2000《水工建筑物抗震设计规范》[26]中指定的加速度反应谱,采用文献[27]中的拟合方法,拟合了12组三向人工地震动作为主震,同时依据式(3)拟合了12条ETA地震动作为余震,将它们随机组合成12条主震-ETA余震序列。主震时长20 s,主震震级考虑Sa(T1)=0.4~1.0g共7个等级,主余震之间间隔5 s,ETA余震时长30 s,最大地震强度为2.0g,因此一共构建了84条不同的主震-ETA余震序列,如图3所示。另外,在计算Cb时,本文采用以ETA地震记录作为单独主震的形式进行分析,以避免IDA中所需的多次计算。需要说明的是,由于本文主要探究主震受损情况下拱坝抗震能力的变化情况,为了使单独主震和主余震序列的计算结果具备可比性,因此并未考虑主震和余震的频谱特征差异。
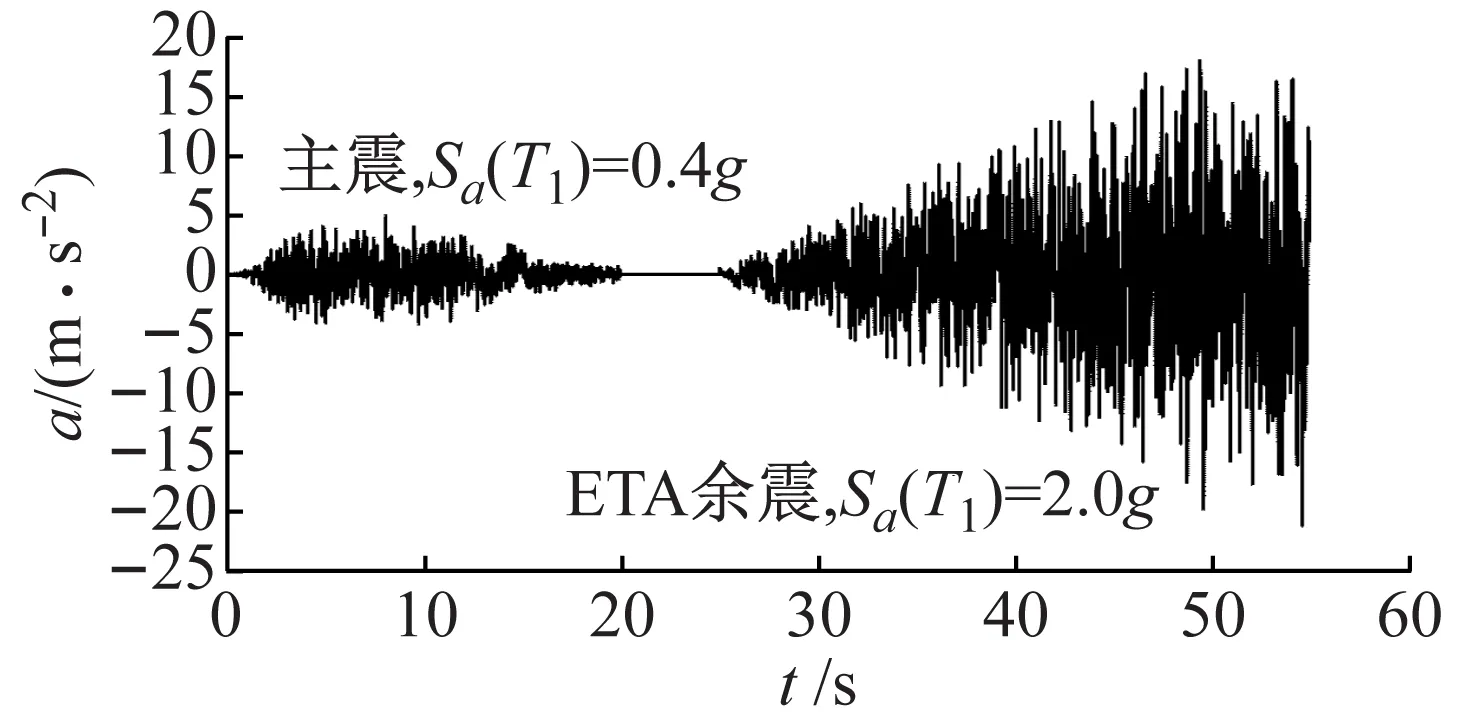
图3 主震—ETA余震示意图
2 高拱坝非线性动力分析
2.1 单独ETA主震分析
首先将ETA地震记录单独作为主震进行动力分析,并求出拱坝的破坏强度Cb。分析中所选择的工程需求参数(engineering demand parameters, EDP)为损伤体积比(Rdt>0)、开裂体积比(Rdt>0.8)和顶拱朝上下游最大动力相对位移(Δu,Δd),其中dt为拉伸损伤因子。图4给出了ETA分析结果中一些EDP随着谱加速度(时间)的变化情况(ETA曲线)。图4中每条ETA曲线都可以等价为一条IDA曲线,与IDA方法类似,ETA分析中损伤与位移结果也随着地震强度的增加不断增大。计算结束时(Sa(T1)=2.0g)损伤体积比Rdt>0和开裂体积比Rdt>0.8都接近100%,上游位移Δu甚至达到了数米,说明此时拱坝损伤非常严重,实际上早在计算结束前就已经破坏。因此,可以根据ETA的计算结果求出每条ETA地震记录对应的Cb。
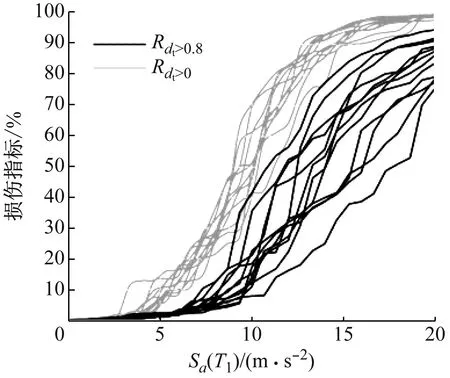
(a) 损伤
为了验证ETA计算结果的合理性,需要将其与IDA的计算结果进行对比。在基于主震-ETA余震序列的动力分析中,将各条主震的计算结果进行汇总便得到IDA的计算结果。图5将单独ETA的计算结果与IDA的计算结果进行了对比。为方便比较,图5中ETA曲线为12个ETA计算工况的平均值。从图5中可以看到,在IDA的强度范围内IDA的损伤结果大致分布在ETA均值的两侧,Rdt>0的吻合情况较好,尤其是在地震强度不大的时候。对Rdt>0.8来说ETA均值处于IDA数据范围中偏下的区域,因此ETA对开裂体积比的结果略低于IDA。位移的差异比损伤差异稍大,在地震强度较小时(约0.6g之前),IDA中Δd与Δu几乎相等,但ETA中Δd均值明显比Δu更大。此外,地震强度较小时ETA与IDA在Δd上并无太大差异,随地震强度增大ETA出现高估Δd的现象,对于Δu而言在IDA的计算范围内ETA偏小。
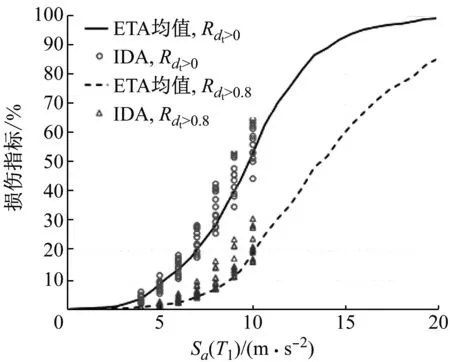
(a) 损伤
综合以上结果,表明在IDA的计算范围内,ETA与IDA的损伤分析结果接近,但位移结果上存在一定区别。与IDA相比,ETA的Δd更大,但Δu更小。整体而言,在所计算的IDA强度范围内ETA的计算结果略微小于IDA,但仍具有可比性。
2.2 极限抗震能力
对于拱坝而言,由于资料有限,在进行数值模拟时对破坏的定义并没有统一标准。目前,包括拱坝动力模型试验在内的一些研究中[28-29]将上下游裂缝贯穿视为拱坝破坏的标志,该方法简单可行,且一定程度上符合人们的直观判断。尽管目前对裂缝贯穿后梁顶自由块体的动力稳定性尚缺乏认识,本文从实践性的角度出发,采用这种方法定义拱坝的破坏,认为当连续两个或以上坝段出现贯穿裂缝时拱坝破坏,并求出对应时刻的地震强度。其中裂缝贯穿的标志是损伤因子dt>0.8的损伤区从下游贯穿至上游,如图6所示。
基于此判定标准,对每条ETA地震记录都能获取对应的破坏强度Cb,并通过矩法[30]拟合出拱坝的破坏易损性曲线,如图7所示,表示某个地震强度下拱坝出现破坏的概率,或拱坝的极限抗震能力等于某个特定值的概率。
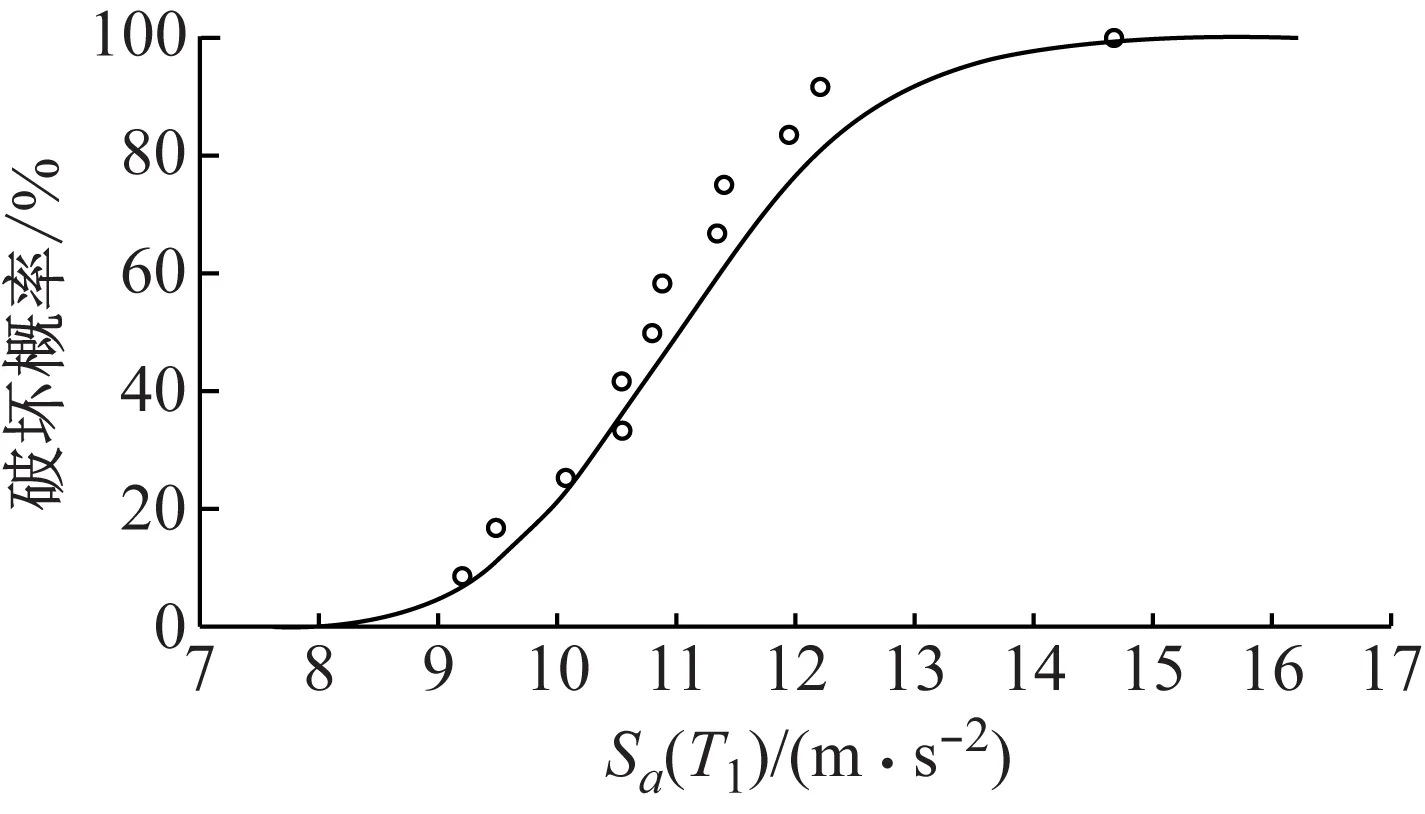
图7 基于ETA分析的拱坝破坏易损性曲线
2.3 主震-ETA余震序列分析
2.1节、2.2节给出的都是单一地震作用下的结果,下面对基于主震-ETA余震序列的动力响应结果进行分析。图8以主震强度Sa(T1)=1.0g的情况为例,给出动力响应结果随时间变化的过程,图8中0~20 s为主震,25~55 s为ETA余震。
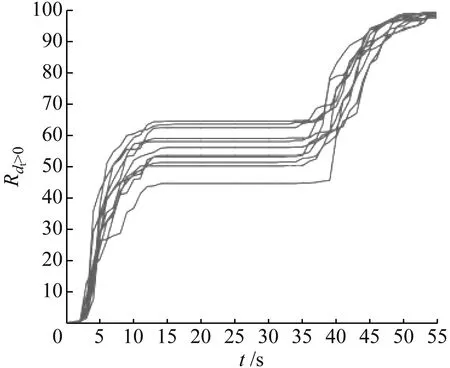
(a) 损伤
图8中动力分析结果随时间的增加过程与单一地震时有明显区别。因为25~30 s为自由振动,余震开始前主震的影响已经衰减到足够小,因此坝体的最大动力响应在该时间范围出现一个平台。这也说明5 s的时间间隔是足够的,不会对余震响应带来影响。进入ETA余震作用时间后,当余震强度较小的时候,坝体最大动力响应保持不变,直到ETA余震的强度超过某一水平后坝体最大动力响应重新增加。然而,需要注意的是ETA余震重新引起坝体最大动力响应增加时对应的时刻(或ETA余震强度)。表1给出了当损伤体积比Rdt>0在ETA余震作用下显著增加(增加10%)时对应的余震强度。
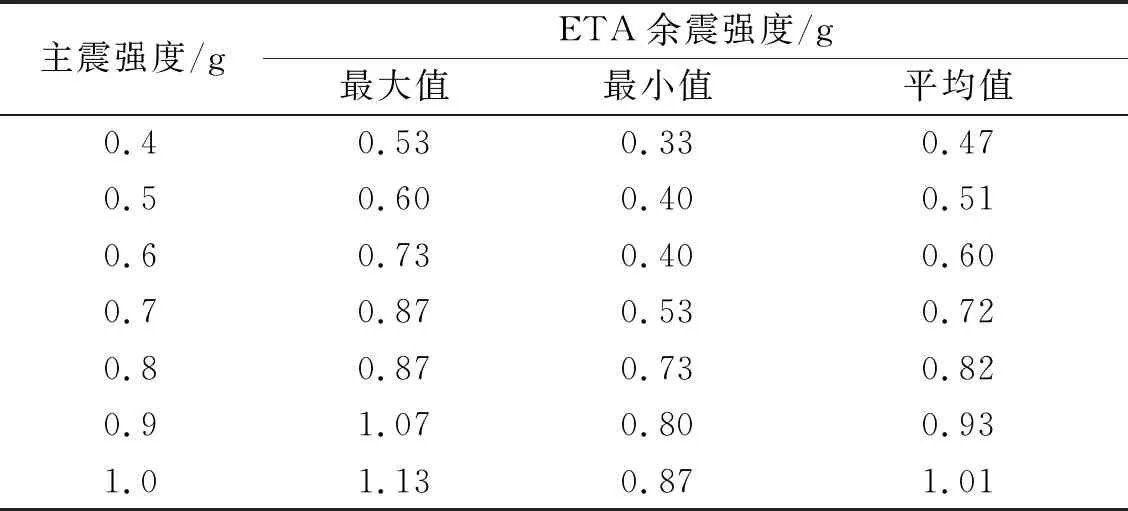
表1 ETA余震引起Rdt>0显著增加时对应的强度
由表1可知,当拱坝动力响应在余震作用下显著增大时,对应的余震强度可能大于或小于主震强度,但平均而言两者相当。这与我们的认知有一定出入,因为大多数情况下研究人员认为坝体一旦产生裂缝就可能在并不强的余震作用下导致裂缝进一步扩展,而表中数据却显示即使对于主震为1.0g的情况(Rdt>0约60%,坝体已明显损伤),余震强度也必须足够大才能使损伤进一步扩展。对于该现象,本文认为一方面它表明拱坝具有良好的抗震性能;另一方面也可能是有限元分析模型的局限性造成的。本文采用的混凝土塑性损伤本构模型本质上是从能量的角度模拟裂缝的生成和扩展,无法从几何上对裂缝进行模拟。从图6的梁截面损伤图也能看出,若以损伤因子dt>0.8定义裂缝,则梁截面上裂缝范围很广且上下连成一片,而现实中混凝土是脆性断裂,其拉裂缝一旦形成则周围混凝土的拉应力得到释放,裂缝宽度应该比较窄。对于混凝土裂缝扩展的模拟一直是热点问题,Pan等采用扩展有限元模拟Koyna重力坝的坝颈拉裂缝,得到较好的模拟效果,但受限于分析理论,该方法暂时无法用于拱坝的三维非线性动力计算。目前,模拟高拱坝坝体混凝土开裂的方法仍然以塑性损伤理论为主,更有效的模拟方式仍需进一步探究。
3 高拱坝极限抗震能力损失
在基于主震-ETA余震序列的动力分析中,当拱坝在主震结束时破坏则认为其没有后续承载能力,抗震能力完全丧失,即dC=100%。若主震结束后拱坝没有破坏,则在ETA余震计算过程求出拱坝破坏对应的破坏强度,即震后的极限抗震能力Cp,然后基于式(4)计算dC。表2给出了主震未引起拱坝破坏时dC的统计值,其中缺省值表示主震导致破坏(dC=100%),表2中平均值的计算并不考虑该种情况。从表2中可以看出,只有主震强度达到一定水平时才会引起拱坝极限抗震能力下降,随着主震强度的增加,主震引起的损伤增大,拱坝极限抗震能力逐渐减小,dC不断增大。图9给出了表2中dC的平均值随着主震强度的变化情况,并对其进行拟合。关于拟合曲线的分布形式有以下两个方面的考虑:首先主震强度为正值,且当主震强度很小时dC接近于0;其次当主震强度很大导致拱坝接近破坏时,dC趋近于1。因此采用对数正态分布比较符合这两种情况。需要指出的是,图9中曲线的拟合是基于最小误差平方和原理进行的,由于数据点只分布在部分强度范围,因此得到的曲线只是对当前数据的估计,当更多数据得到补充时,曲线的形状可能会有所变化。
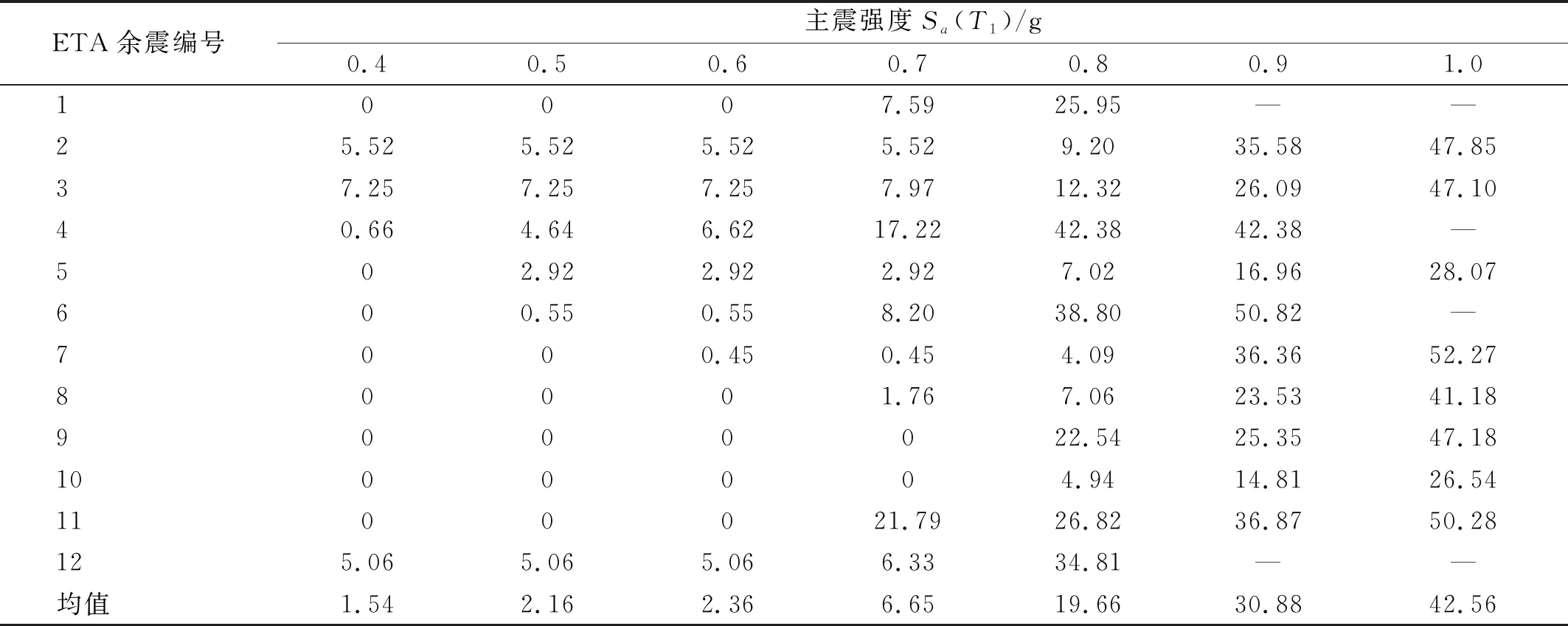
表2 主震未引起拱坝破坏时dC的统计
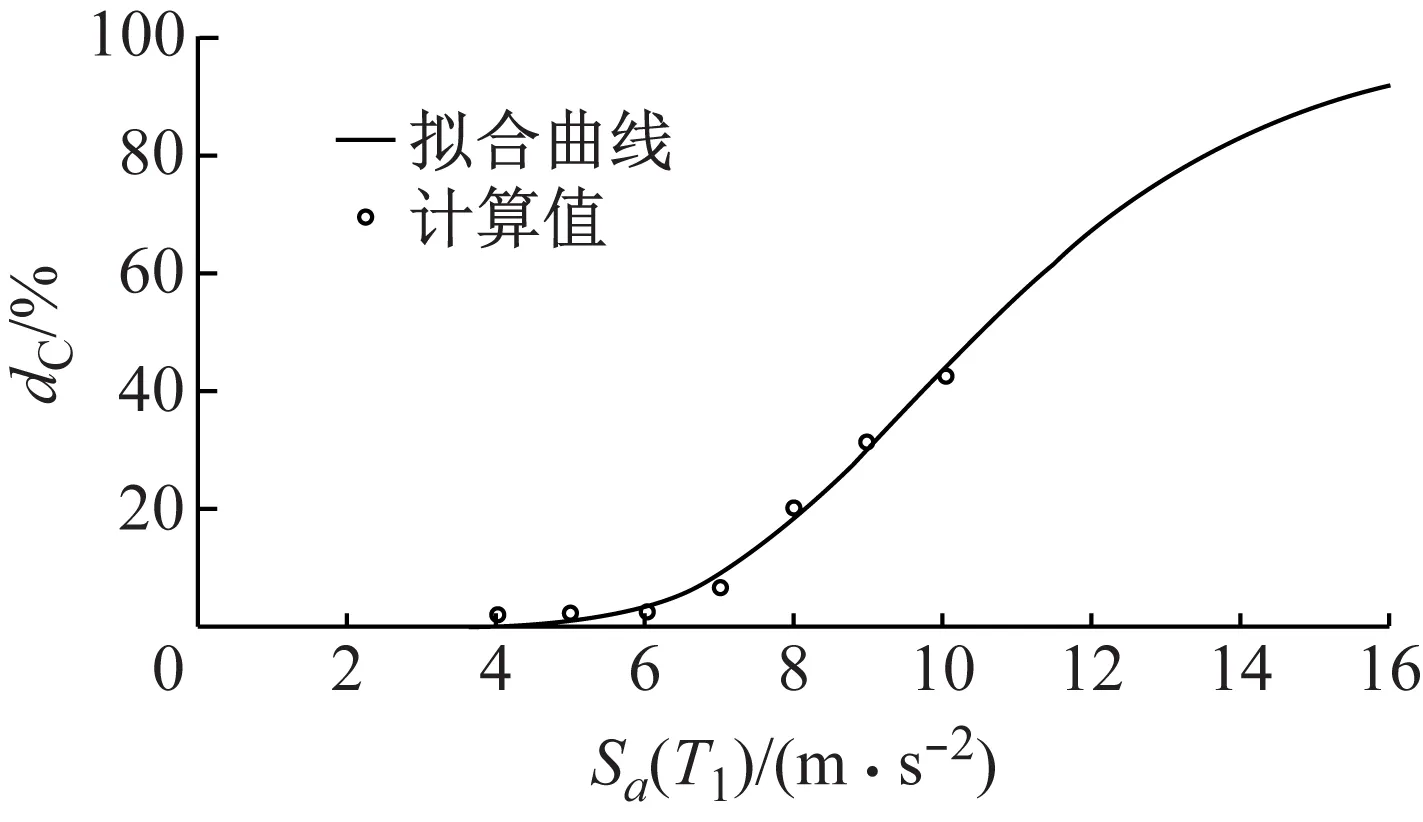
图9 主震未引起拱坝破坏时dC(均值)随主震强度变化情况
考虑到主震有可能引起拱坝破坏,因此结合图7的拱坝破坏易损性曲线,对每个主震等级下的dC进行加权处理
dC|IM=im=P[D|IM=im]×1 +(1-P[D|IM=im])×dC|ND,IM=im
(5)
式中:IM为主震强度;im为具体强度值,即Sa(T1)的值;P[D|IM=im]为给定主震强度下拱坝破坏的概率,可通过破坏易损性曲线求出;dC|ND,IM=im为主震未导致破坏时dC的期望值,可以通过图9的拟合曲线得到;dC|IM=im为考虑主震引起破坏时给定主震强度下dC的期望值。
dC|IM=im随主震强度变化情况(极限抗震能力损失曲线)如图10所示,同时也给出了图9中不考虑主震破坏的情况作为对比。很显然,由于考虑了主震引起破坏的可能性,主震强度较大时dC的期望值显著增大了。此外,当主震强度较小时,拱坝很可能保持完好无损,因此极限抗震能力几乎不发生损失,dC的期望值接近0。随着主震强度的增大,dC的期望值也迅速增大,当拱坝接近破坏时逐渐趋近100%。根据现行GB 51247—2018《水工建筑物抗震设计规范》[31]中拱坝的标准设计反应谱,大岗山拱坝在设计地震下的Sa(T1)为6.94 m/s2,由图10可知设计地震引起极限抗震能力损失的期望值小于10%,因此坝体预期能经受设计地震并仍有较强的抗震能力。
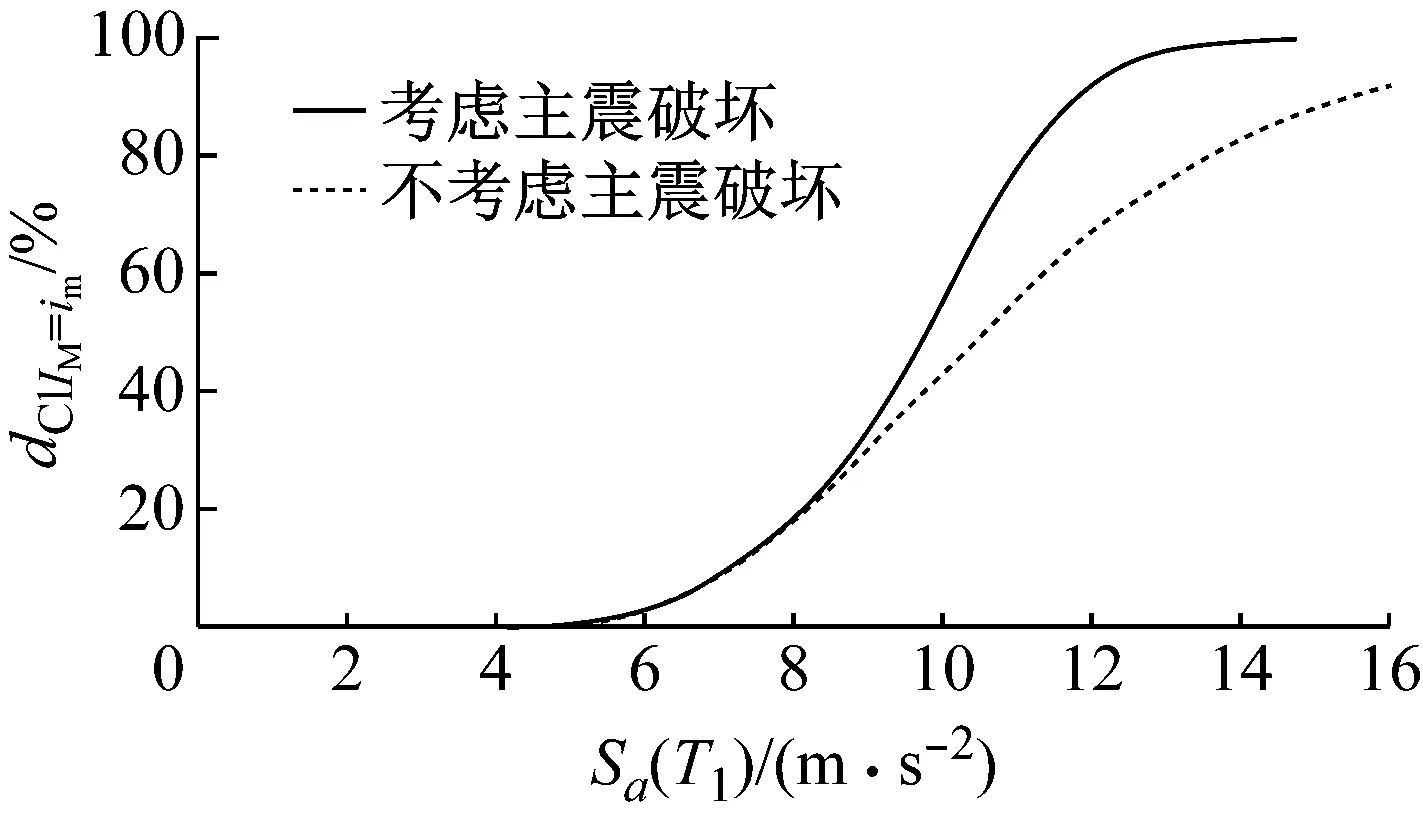
图10 拱坝极限抗震能力损失曲线
4 结 论
本文对拱坝在遭受主震损伤后的极限抗震能力进行了研究,提出了极限抗震能力损失的概念。基于耐震时程分析法(ETA)拟合了ETA地震记录,并构建了主震-ETA余震序列对大岗山拱坝进行了动力分析,最终给出大岗山拱坝的极限抗震能力损失曲线。本文得出的主要结论如下。
(1) ETA与IDA的计算结果具备一定可比性,但两者并不严格等效。当目标加速度谱一样时,ETA略微低估了坝体损伤和顶拱上游位移,高估了顶拱朝下游的位移,总的来说低估了坝体的动力响应程度。
(2) 当采用塑性损伤模型模拟坝体混凝土开裂时,拱坝的损伤在主震-ETA余震序列计算过程中逐渐累积,并在主震结束后保持一段时间的恒定。ETA余震开始作用后拱坝的损伤并不会立即恢复增加,且只有当ETA余震强度和主震强度相当时才能使损伤结果出现显著增加。
(3) 主震达到一定强度时会引起坝体损伤,这导致拱坝的极限抗震能力出现一定程度的损失,且随着主震强度增大,拱坝极限抗震能力的损失程度也随之增大。就本文的计算结果而言,设计地震作用下大岗山拱坝极限抗震能力损失的期望值小于10%,坝体仍有较强抗震能力。
极限抗震能力损失曲线可以对未知地震的危害做出定量评价,作为工程决策的参考手段。后续的研究可以考虑针对此概念进行完善,丰富极限抗震能力损失的评价手段,并采用更合理的方法构建主余震序列,以提高分析结果的可靠程度。
