多层堆叠式永磁动力减振刀杆设计与仿真分析
2022-02-22刘保钟孙铁伟
王 民, 刘保钟, 秦 鹏, 孙铁伟
(1. 北京工业大学 机械工程与应用电子技术学院 先进制造技术北京市重点实验室, 北京 100124;2. 电火花加工技术北京市重点实验室, 北京 100191)
目前长径比大于4的大长径比铣刀在铣削加工过程中的振动控制方式,主要为在刀杆内部空腔安装动力减振器,这种减振方式结构简单、不需要外界能量输入、减振效果良好,因此得到了广泛应用[1-3]。但传统内置式动力减振器中的刚度和阻尼主要由橡胶和阻尼液提供,工作过程中易发生橡胶疲劳老化和阻尼液泄露等问题,且由于阻尼和刚度不能独立精准设计,使用过程中调节困难,因此动力减振器往往不能达到最优减振效果[4-6]。
针对上述问题,国内外专家学者尝试利用非接触式磁力提供动力减振器刚度。例如Sodano等[7]从电涡流和磁阻尼的产生机理出发,综合介绍了多种涡流阻尼制动和减振研究方法,并对其潜在的应用场景进行讨论。Ebrahimi等[8]设计了不同结构的涡流被动阻尼器,并利用解析法和有限元分析得到了最佳设计尺寸,大大提高了阻尼系数。Karnopp[9]针对车辆悬挂系统中的电磁阻尼减振器,通过改变外部线圈电阻设计了电动可变减振阻尼器,这种无芯设计显著减小了减振单元质量。目前由于永磁材料的磁性限制,基于磁力的减振器主要为电磁式动力减振器或应用于工程建筑的大尺寸动力减振器,例如陈政清等[10]研究了板式电涡流动力减振器,应用于大跨度拱形桥、人行桥的振动控制。方重等[11]设计了一种单摆式电涡流调频质量阻尼器,并对其阻尼特性进行试验分析,验证其地震响应控制效果。
本文针对大长径比铣刀设计了一种多层堆叠式永磁动力减振器(以下简称永磁动力减振器),同时利用磁刚度和电涡流阻尼提供永磁动力减振器所需刚度和阻尼。整体采用独特的堆叠式结构可以保证永磁动力减振器在较小体积下提供更大的磁刚度和电涡流阻尼。与传统动力减振器相比,本文所设计的永磁动力减振器中磁力和电涡流阻尼力均为非接触式,工作过程中不会产生磨损老化等问题,可以有效提升动力减振器的工作稳定性,提高使用寿命。本文分别建立了多层堆叠式永磁动力减振器中磁刚度和电涡流阻尼的理论计算模型,利用MATLAB软件和有限元电磁仿真软件Maxwell分别探究了磁刚度和电涡流阻尼与永磁动力减振器各部分结构尺寸之间的关系。最后利用MATLAB软件分别对安装永磁动力减振器的铣刀和等尺寸实心铣刀进行数值仿真分析,对比其频响函数幅值的变化情况。研究结果表明,安装永磁动力减振器后刀杆的频响函数幅值最大值下降91.1%,具有良好的减振效果。
1 永磁动力减振刀杆结构
本文所设计的永磁动力减振刀杆结构,如图1所示。其主要由屏蔽壳、永磁动力减振器、端部永磁体和刀杆组成。永磁动力减振器位于刀杆的圆柱空腔内,永磁动力减振器和刀杆之间通过屏蔽壳隔开,屏蔽壳的材料为一种高电阻率、低损耗的高磁导率合金,其具有良好的隔磁性能,可以大大降低刀杆作为导磁体对磁刚度和电涡流阻尼的影响。
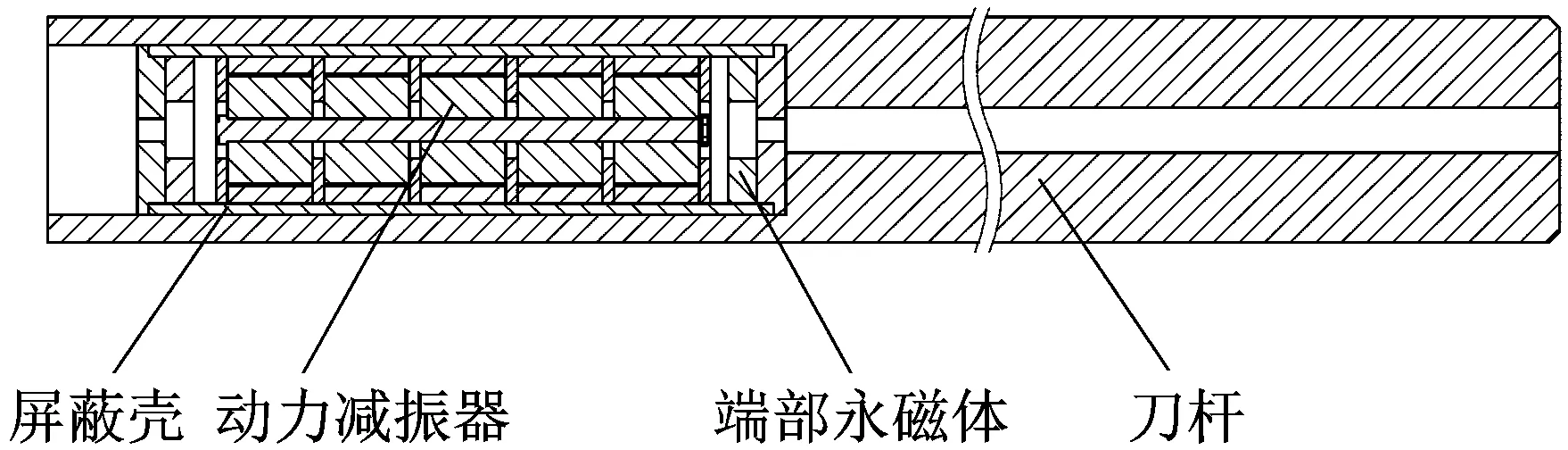
图1 永磁动力减振刀杆剖面
永磁动力减振器结构,如图2所示。其整体由一定数量的金属片、橡胶垫片、芯轴、内磁环和外磁环叠加排列组成。这种堆叠式排列结构在不改变整体轴向长度的前提下,通过增加磁环个数增加磁极面个数,可以在一定限度内提升磁刚度和电涡流阻尼[12-14]。
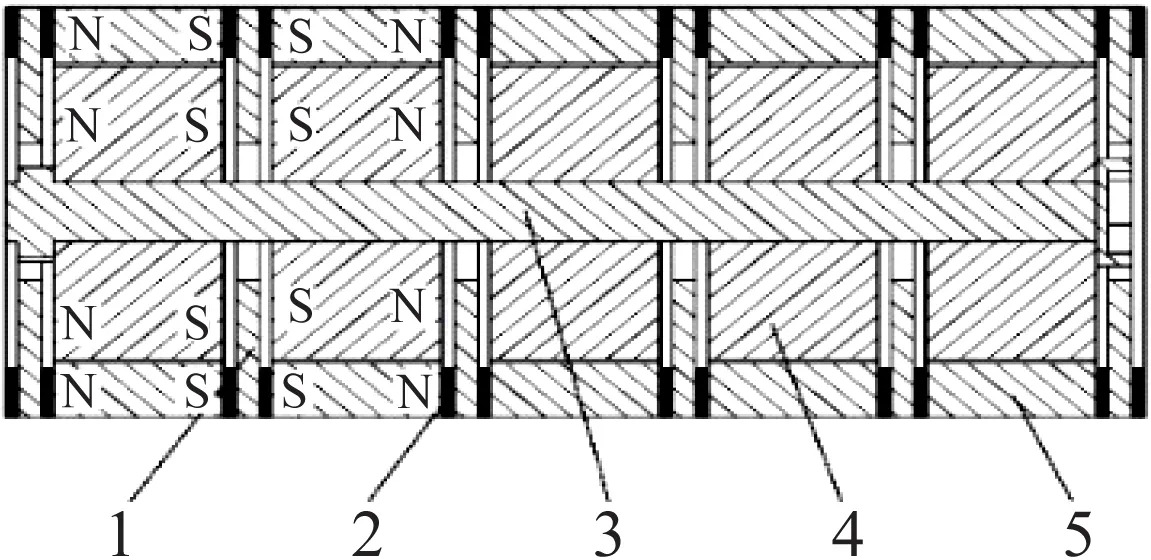
1. 金属片; 2. 橡胶垫片; 3. 芯轴; 4. 内磁环; 5. 外磁环。
永磁动力减振器中永磁材料为稀土永磁材料铷铁硼,金属片的材料为电导率较高的黄铜。所有内磁环均通过芯轴连接组成振子,内、外磁环之间留有一定的径向间隙,保证内磁环始终处于磁悬浮状态,在工作过程中内磁环可以在外磁环内做径向往复运动。一个内磁环和对应的外磁环组成一组磁环对,相邻磁环对之间由一个金属片和两个橡胶垫片隔开。永磁动力减振器中所有磁环的磁化方向均为轴向,其中同组磁环对中磁环的磁极安装方向相同,相邻磁环对间的磁极安装方向相反,磁环间的磁刚度大小与磁环的磁化方向无关[15]。
2 磁力计算
目前针对磁环间磁力的计算方法多为等效磁荷法和解析模型法,其中解析模型法是利用复变函数保角变换,将具有径向偏移的磁环间磁场转换为对称磁场进行求解,这种方法基于较多假设,计算结果误差较大[16-17]。
本文采用等效磁荷法计算磁环间磁力,这种计算方法基于更少的假设和前提,计算结果更加准确。但其计算模型包含四重积分,不能直接得到磁力和相关参数之间的关系,且数值仿真中计算量巨大,因此采用蒙特卡罗法的统计试验方法进行磁力的数值仿真[18-20]。
2.1 永磁动力减振器磁力计算模型
以永磁动力减振器中相邻磁环对为例,建立磁化模型,如图3所示。磁环间的磁力为所有磁环端面上等效磁荷间相互作用力的叠加。
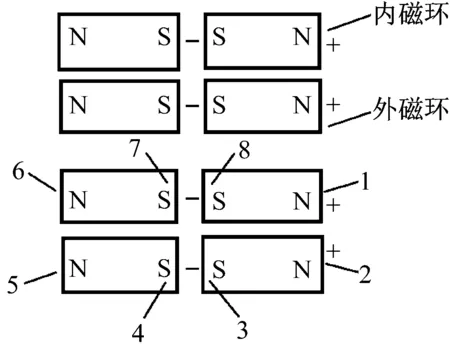
图3 磁环磁化模型
建立磁环间磁荷作用力关系模型,如图4所示。计算磁环端面1、2上A、B两点间的磁力。
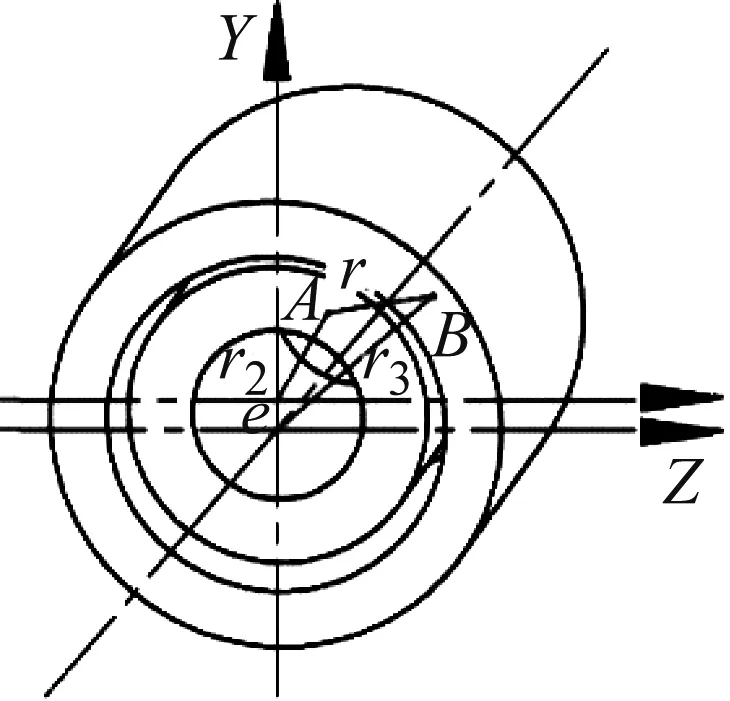
图4 磁环间磁荷作用关系模型
首先求出A、B两点处的磁荷量
q2=δ·r2·dα·dr2
(1)
q3=δ·r3·dβ·dr3
(2)
A点处的磁荷在B点处的磁场强度为
(3)
则B点电磁荷受到的磁场力为
dF=H1·q3=H1·δ·r3·dβ·dr3
(4)
(5)
式中:δ为磁荷面密度;μ0为真空磁导率;r为内外磁环端面上A、B点端面之间的距离;(r2,α)为内磁环端面上A点的极坐标;(r3,β)为外磁环端面上B点的极坐标;r0为与向量r方向相同的单位向量。
(6)
则A、B两点之间的磁力为
(7)
针对轴向磁化的磁环可知
δ=j′·n=μ0·M·n
(8)
B=μ0(H+M)
(9)
式中:j′为磁极化强度矢量;n为磁环端面法线方向的单位矢量;M为磁化强度矢量;H为磁场强度矢量;B为磁感应强度矢量。
针对钕铁硼永磁材料,其退磁曲线如图5所示。
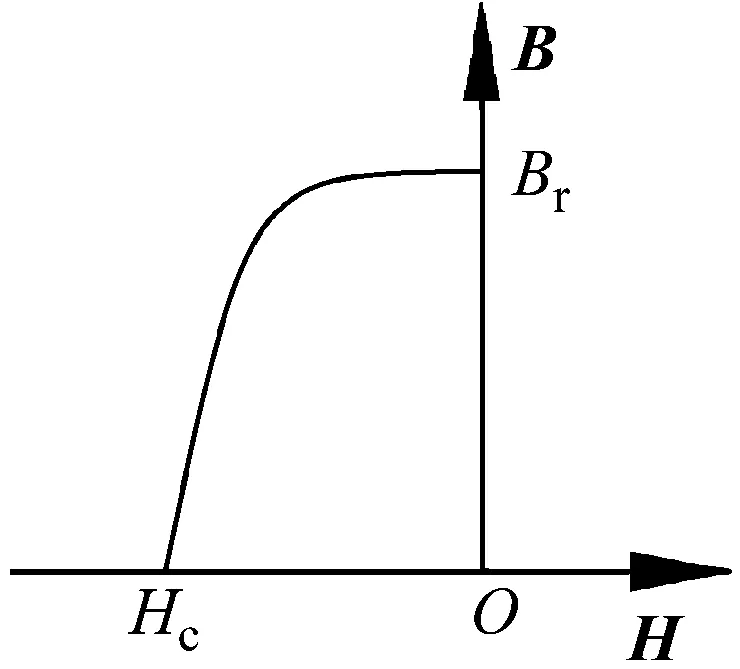
图5 永磁材料退磁曲线
图5中:Br为剩余磁感应强度;Hc为矫顽磁力。由退磁曲线可以知,当H=0时,B=Br,由此可知,Br=μ0M。
针对轴向磁化的磁环,其磁化方向和磁环端面法线方向重合,综合以上分析可知
δ=μ0M=Br
(10)
将式(10)代入式(7)可知
(11)
将式(11)沿着Y方向投影,进而求出A、B两点磁荷间的径向作用力。建立A、B两点磁荷间的矢量关系,如图6所示。
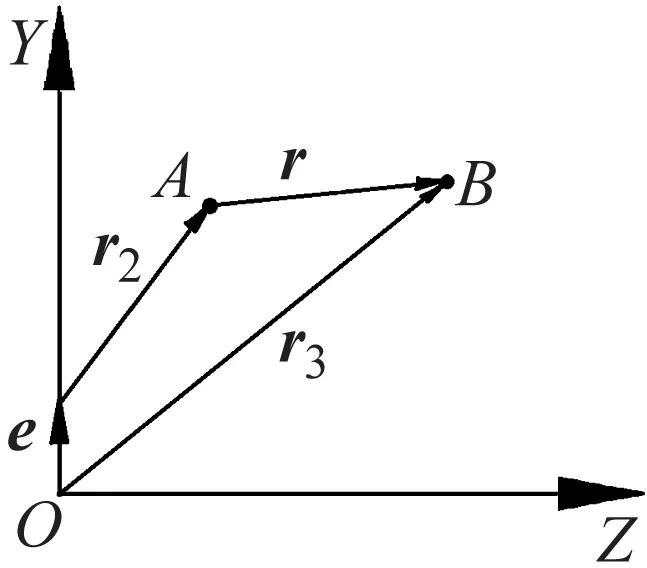
图6 磁荷间矢量关系
由图6可知
r=r3-(r2+e)
(12)
r·j=r3·j-(r2+e)·j
(13)
r·u=r3·u-(r2+e)·u
(14)
式中:j和u分别为Y轴和Z轴方向的单位矢量;r3·j=r3·cosβ;r2·j=r2·cosα;e·j=e;r3·u=r3·sinβ;r2·u=r2·sinα;e·u=0。
根据几何关系可知
(15)
式中,e为内磁环相对外磁环的径向偏移量(以下简称径向偏移量)。
将式(15)代入式(11),并对整个磁环端面进行积分,求出同组磁环对的同侧端面之间的径向磁力F1
(16)
式中:R1为内磁环内径;R2为内磁环外径;R3为外磁环内径;R4为外磁环外径。
同理,求出同组磁环中异侧磁环端面径向磁力F2为
(17)
式中,L为磁环长度。
相邻磁环对的磁环端面间的径向磁力F3为
(18)
式中,x0为磁环对和磁环对之间的轴向间隙。
等效磁荷法计算磁环间磁力时,包含同种磁荷的磁环端面间磁力为正,包含异种磁荷的磁环端面间磁力为负,求出n层堆叠式永磁动力减振器中的磁环间径向磁力
F′=2n(F1-F2)+2(n-1)F3
(19)
2.2 磁刚度和尺寸参数关系
从磁力计算模型可以看出,动力减振器中磁环间径向磁力和内磁环内径R1、内磁环外径R2、外磁环内径R3、外磁环外径R4、磁环对和磁环对之间的轴向间隙(以下简称磁环对轴向间隙)x0、磁环长度L、径向偏移量e等参数有关。
由于外磁环外径和刀杆空腔半径相同,内磁环的内径与连接杆半径相同。因此本文主要分析内磁环外径R2、磁环长度L、径向偏移量e和磁环对轴向间隙x0这4个参数对磁力的影响。
利用MATLAB软件对5层堆叠式永磁动力减振器的磁力进行数值仿真分析,探究磁力与径向偏移量e之间的变化关系。综合考虑刀杆尺寸,假设内磁环内径R1为2 mm、内磁环外径R2为5.5 mm、外磁环内径R3为5.8 mm、外磁环外径R4为8 mm、磁环长度L为7 mm、磁环对轴向间隙x0为1 mm。求出此时径向磁力和径向偏移量e之间关系,如图7所示。由图7可知,磁环间径向磁力与径向偏移量e之间近似为线性关系,即磁环间径向磁刚度可视为定值。
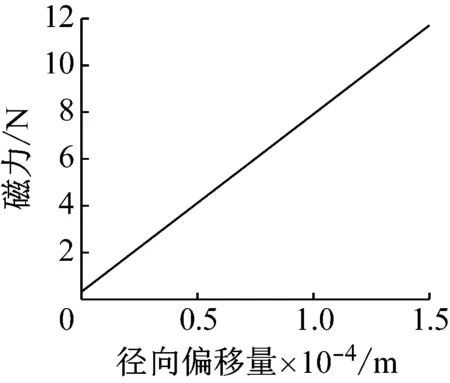
图7 磁环径向磁力与径向偏移间关系
保持上述尺寸参数不变,设置径向偏移量e为0.15 mm,当磁环对轴向间隙x0的变化范围为0~3 mm时,求出磁刚度与磁环对轴向间隙x0之间关系,如图8所示。
由图8可知,随着磁环对轴向间隙x0逐渐增加,磁刚度逐渐下降,且下降趋势趋于平缓,当磁环对轴向间隙x0>2.7 mm时,磁刚度基本保持不变。

图8 磁刚度和磁环对轴向间隙之间关系
保持上述尺寸参数不变,设置磁环对轴向间隙x0为2.4 mm,内磁环和外磁环间径向间隙为0.3 mm,当内磁环外径R2的变化范围为3~7 mm时,求出磁刚度与内磁环外径R2之间关系,如图9所示。
由图9可知,随着内磁环外径R2逐渐增加,永磁动力减振器的磁刚度先增大后减小,当内磁环外径为5.5 mm时,磁刚度达到最大值。
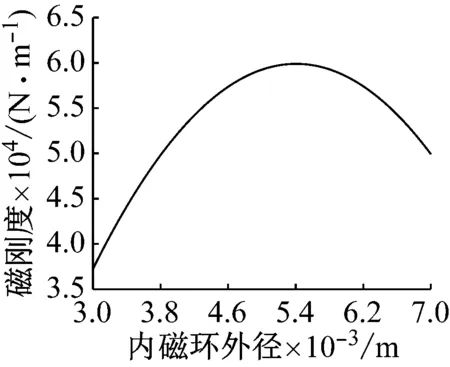
图9 磁刚度和内磁环外径之间关系
保持上述磁环尺寸参数不变,设置径向偏移量e为0.15 mm,磁环对轴向间隙x0为2.4 mm,当磁环长度L变化范围为0~5 mm时,求出磁刚度与磁环长度L之间关系,如图10所示。
由图10可知,磁刚度随磁环长度L增加逐渐增加,且增加趋势逐渐趋于平缓,当磁环长度L>4 mm时,磁刚度基本保持不变。
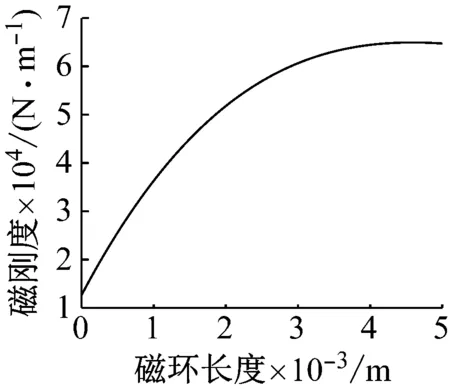
图10 磁刚度和磁环长度之间关系
3 电涡流阻尼计算
永磁动力减振器中电涡流产生机制,如图11所示。当内磁环做径向往复振动时,内磁环和金属片之间发生相对运动,金属片在运动磁场中切割磁感线会产生电涡流,进而产生阻碍这种相对运动的电磁阻尼力。这种阻力的大小和相对速度的大小成正比,阻力方向始终和相对运动方向相反,其特性与一般的黏性阻尼力一致,可以代替传统动力减振器中阻尼液的阻尼作用。
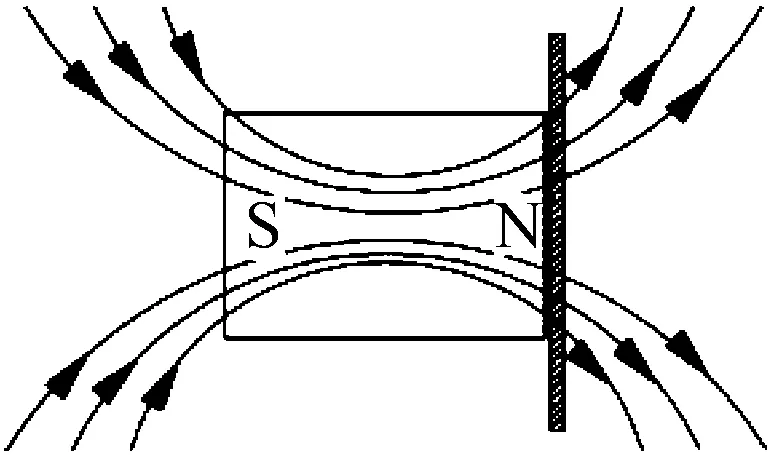
图11 电涡流阻尼产生机制
3.1 磁感应强度计算
由于内磁环的内孔较小,对磁力的影响可以忽略,因此建立电涡流阻尼力理论计算模型时将内磁环简化为圆柱永磁体,建立磁场模型如图12所示。
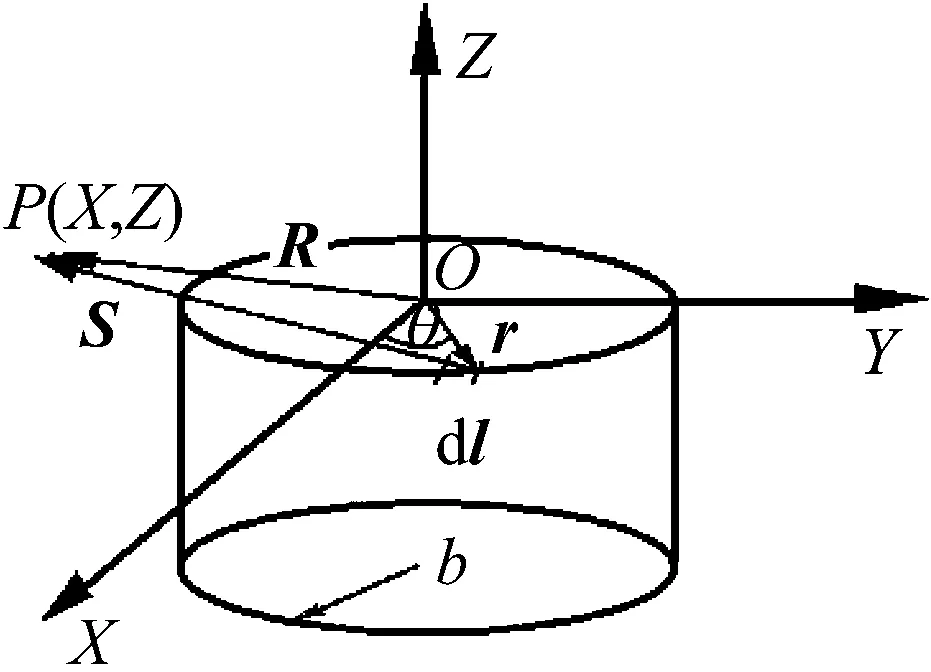
图12 圆柱永磁体磁场模型
以圆柱永磁体上表面中心为原点,建立柱坐标系,依据毕奥-萨伐尔定律求出永磁体表面电流微元Idl对YOZ平面上某一点P处产生的磁感应强度dB。
(20)
其中
S=R-r
(21)
r=b·cosθ·i+b·sinθj
(22)
R=x·i+z·u
(23)
dl=-b·sinθ·dθ·i+b·cosθ·dθ·j
(24)
式中:M1为永磁体的饱和磁化强度,M1=IL0,I为永磁体表面等效电流,L0为圆柱永磁体高度;b为圆柱永磁体半径;μ0为真空磁导率;S为效电流微元到目标点的距离;R为等效电流微元到目标点的矢量;θ为在柱坐标系中从正Z轴来看自X轴逆时针方向转到电流微元dl处所转过的角;i为X轴方向的单位矢量。
对式(20)进行环向和轴向积分,求出永磁体整体在点P处的轴向磁感应强度BZ
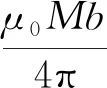
(25)
式中:z′为积分变量;x、z为空间坐标系的坐标。
3.2 电涡流阻尼系数计算
当永磁体与金属片之间发生相对运动时,金属片上产生的电流密度矢量为
J=σ(v×B)
(26)
式中:J为电流密度矢量;σ为金属片的电导率;v为永磁体的速度矢量;B为磁感应强度矢量。由于只考虑永磁体的径向往复运动,因此径向磁感应强度矢量和运动方向平行,不产生电涡流。
求出金属片产生的电涡流阻尼力为
(27)
式中:vr为永磁振子的径向运动速度大小;V为体积分符号。
将式(25)代入式(27),并将体积分转换为单重积分形式
(28)
(29)
式中:r1为金属片内孔半径;r2为金属片外孔半径;X0为金属片和磁环对轴向间隙;H0为金属片厚度;Z为体积分符号。
电涡流阻尼等效阻尼系数w为
(30)
将式(29)代入式(30)求出电涡流等效阻尼系数w
(31)
包含n组磁环对的单层永磁动力减振器的电涡流阻尼系数为
w1=2n×w
(32)
3.3 电涡流阻尼系数和各尺寸参数关系
从电涡流阻尼理论计算模型可以看出电涡流阻尼与永磁体半径b、永磁体高度L0、金属片厚度H0、金属片内孔半径r1、金属片外孔半径r2以及金属片和磁环对轴向间隙X0等参数有关。
通过对永磁动力减振器中磁刚度的计算分析,可以确定永磁体半径和高度,金属片内外径由刀杆空腔半径和连接杆半径确定,因此电涡流设计过程中仅需要探究金属片厚度H0、金属片和磁环对轴向间隙X0对电涡流阻尼的影响即可。
利用MATLAB软件对5层堆叠式永磁动力减振器的电涡流阻尼进行数值仿真。设置永磁体半径b为5.5 mm、永磁体高度L0为7 mm、金属片内孔半径r1为3 mm、金属片外孔半径r2为8 mm、金属片和磁环对轴向间隙X0为0.2 mm。当金属片厚度H0的变化为0~2.5 mm时,求出电涡流阻尼与金属片厚度H0的变化关系,如图13所示。由图13可知,随着金属片厚度的增加,电涡流阻尼逐渐增加,增加趋势逐渐趋于平缓。

图13 电涡流阻尼与金属片厚度关系
设置金属片厚度H0为2 mm,保持尺寸参数不变,当金属片和磁环对轴向间隙X0变化范围为0~0.5 mm时,求出永磁动力减振器电涡流阻尼与金属片和磁环对轴向间隙X0间关系,如图14所示。由图14可知,电涡流阻尼随着金属片和磁环对轴向间隙增加逐渐减小。
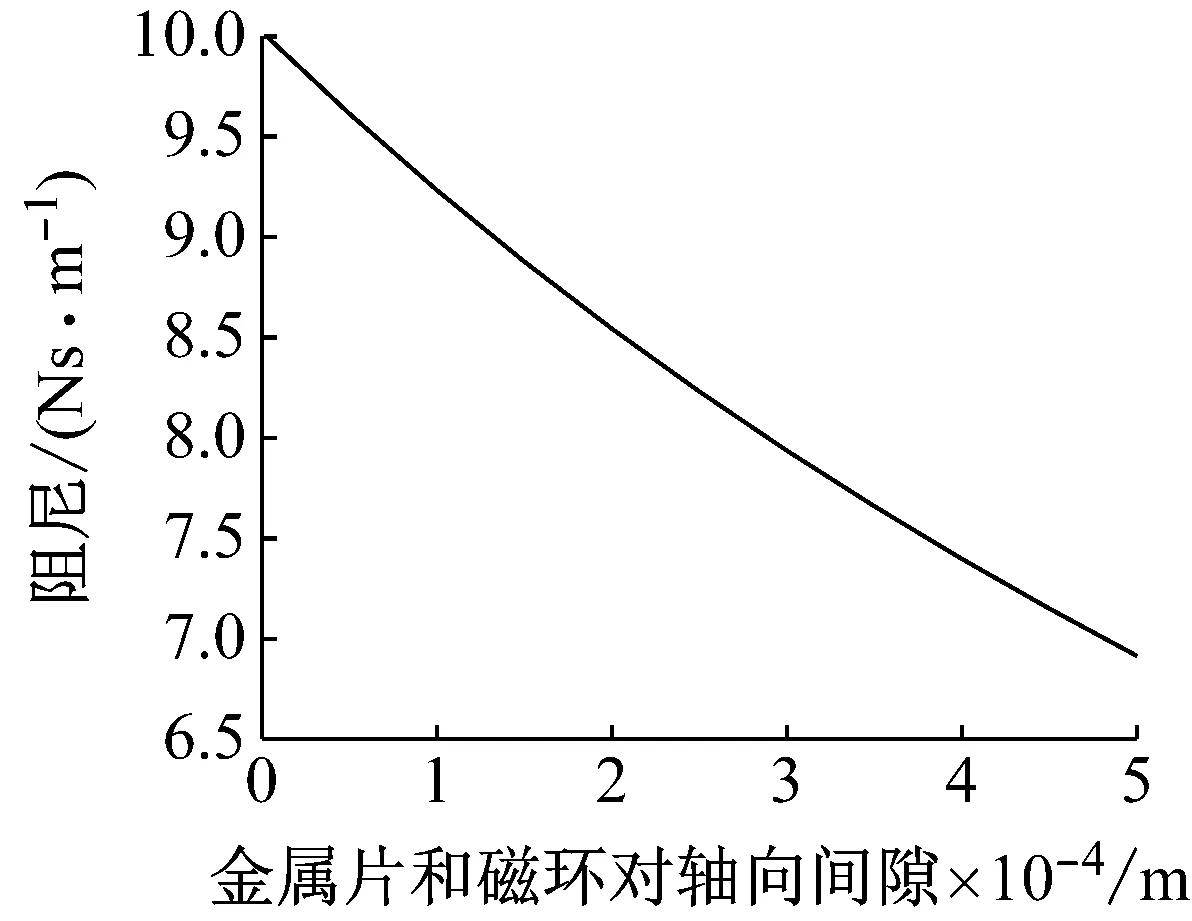
图14 电涡流阻尼与金属片和磁环对轴向间隙关系
4 有限元磁场仿真
利用有限元电磁仿真软件Maxwell分别对永磁动力减振器中的磁力和电涡流阻尼力进行有限元仿真分析,验证2.2节和3.3节MATLAB软件数值仿真结果。Maxwell软件是由ANSOFT公司研发的一款专门针对电磁场分析的仿真软件,可以进行二维和三维的静电场、静磁场、瞬态电场和瞬态磁场仿真计算,常用来分析电机、变压器、传感器和永磁设备等电磁装置[21-22]。
4.1 有限元磁力仿真
利用Maxwell仿真软件中的3D静磁场模块对磁力进行仿真,简化对永磁体磁性影响较小的芯轴部分。建立有限元仿真模型,如图15所示。其中:外磁环外径为8 mm;外磁环内径为5.8 mm;内磁环外径为5.5 mm;磁环长度为7 mm;磁环对轴向间隙为2.4 mm。

图15 堆叠式动力减振器有限元仿真模型
设置永磁材料为NdFeB35,剩磁强度为1.23 T,相对磁导率为1.099 8,矫顽磁力为-8.9×105A/m,磁环的磁化方向为轴向,计算域region大小设置为100%,网格划分中region、外磁环和内磁环的最小网格尺寸分别为5 mm、3 mm和2 mm。
以径向偏移量e为扫描参数,e的变化范围为0~0.15 mm,步长为0.01 mm,求出内、外磁环间径向磁力随径向偏移量变化的有限元仿真结果和理论计算对比曲线,如图16所示。
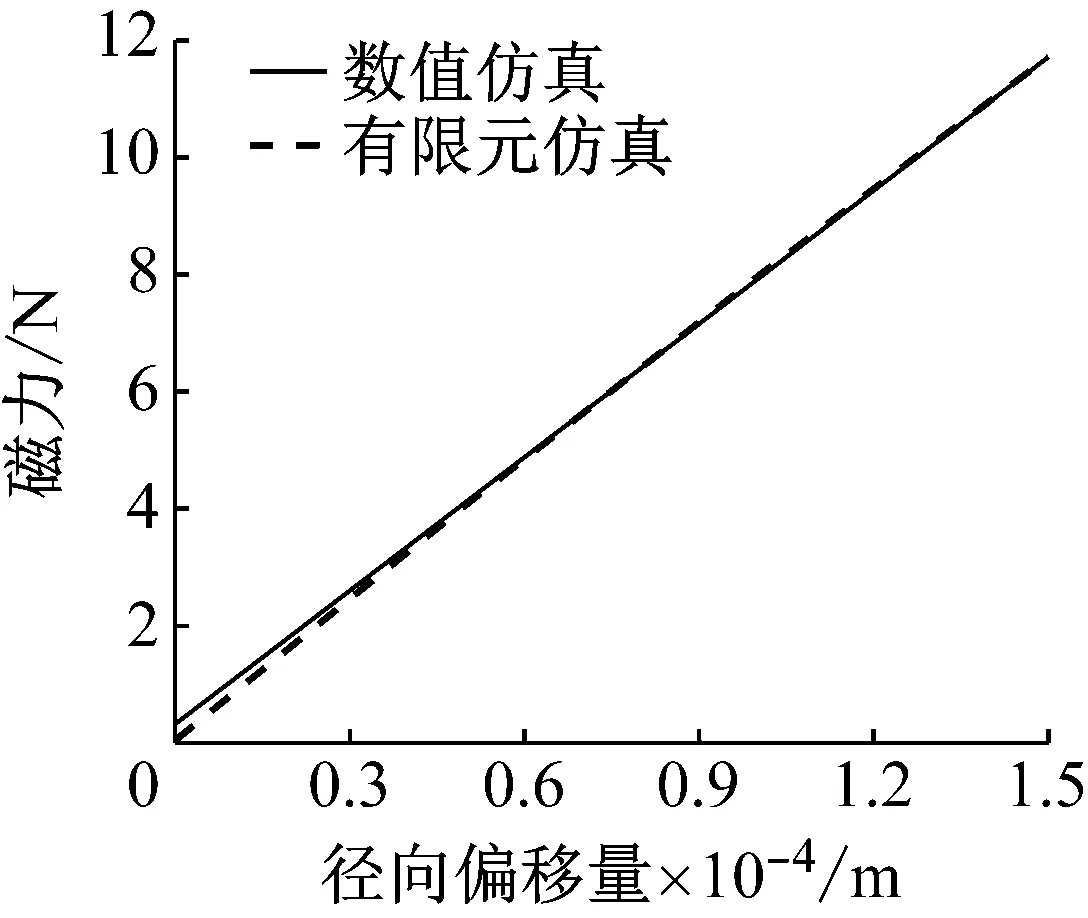
图16 磁力随径向偏移量变化的仿真与计算对比曲线
磁环间径向磁力随径向偏移量变化的有限元仿真和理论计算结果对比,如表1所示。
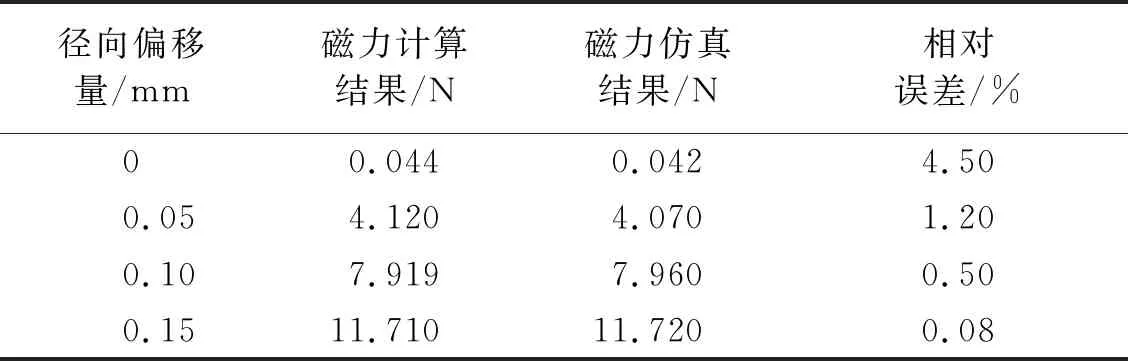
表1 磁力随径向偏移量变化的计算结果与仿真结果
设置磁环间径向偏移量e为0.15 mm,保持其他参数不变,以磁环对轴向间隙x0为扫描参数,参数x0变化范围为0~3 mm,计算步长为0.01 mm,求出此时磁刚度随磁环对轴向间隙变化的有限元仿真和理论计算对比曲线,如图17所示。
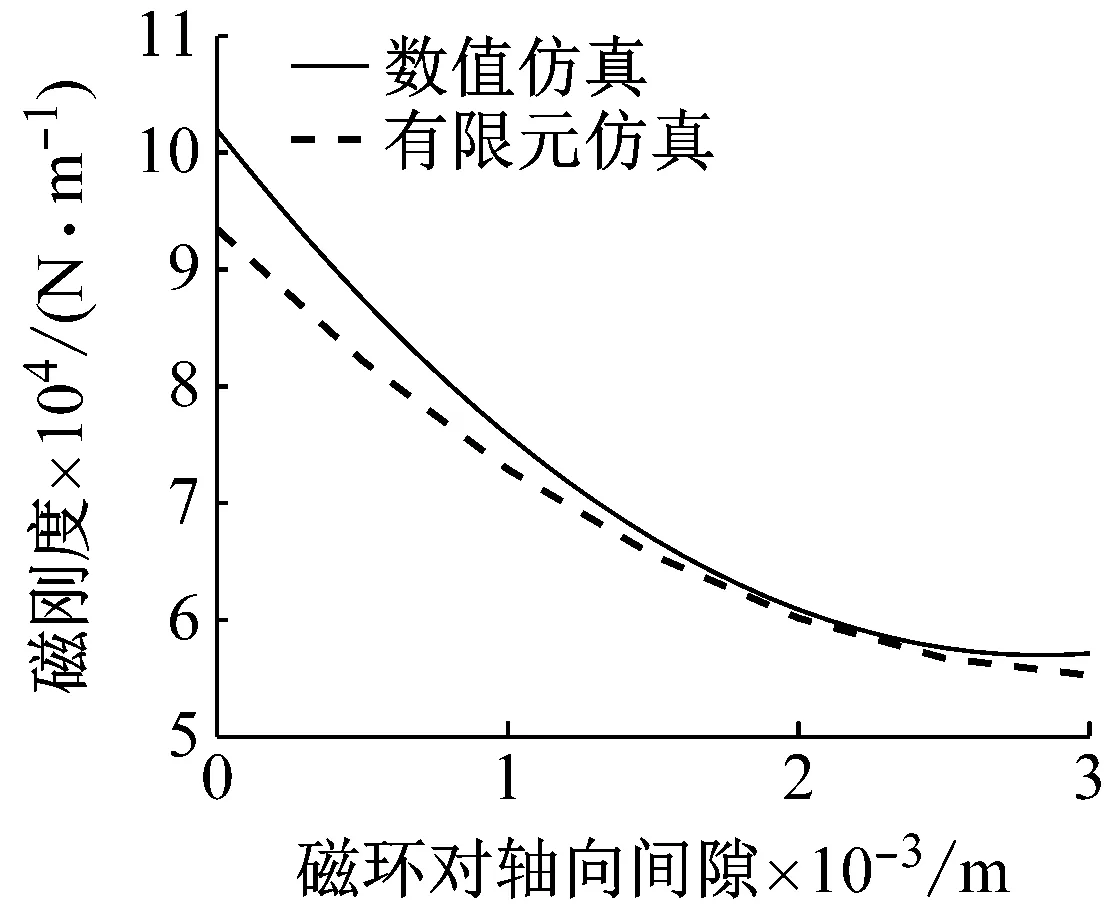
图17 磁刚度随磁环对轴向间隙变化的仿真与计算对比曲线
磁刚度随磁环对轴向间隙变化的有限元仿真和理论计算结果对比,如表2所示。
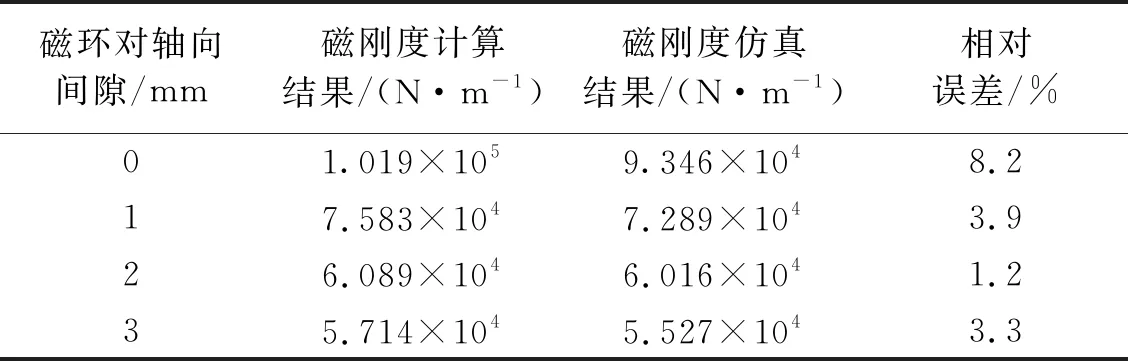
表2 磁刚度随磁环对轴向间隙变化的计算结果与仿真结果
设置径向偏移量e为0.15 mm,磁环对轴向间隙x0为2 mm,保持其他尺寸参数不变,以内磁环外径R2为扫描参数,参数R2变化范围为3~7 mm,计算步长为0.1 mm,求出此时磁刚度随内磁环外径变化的有限元仿真和理论计算对比曲线,如图18所示。
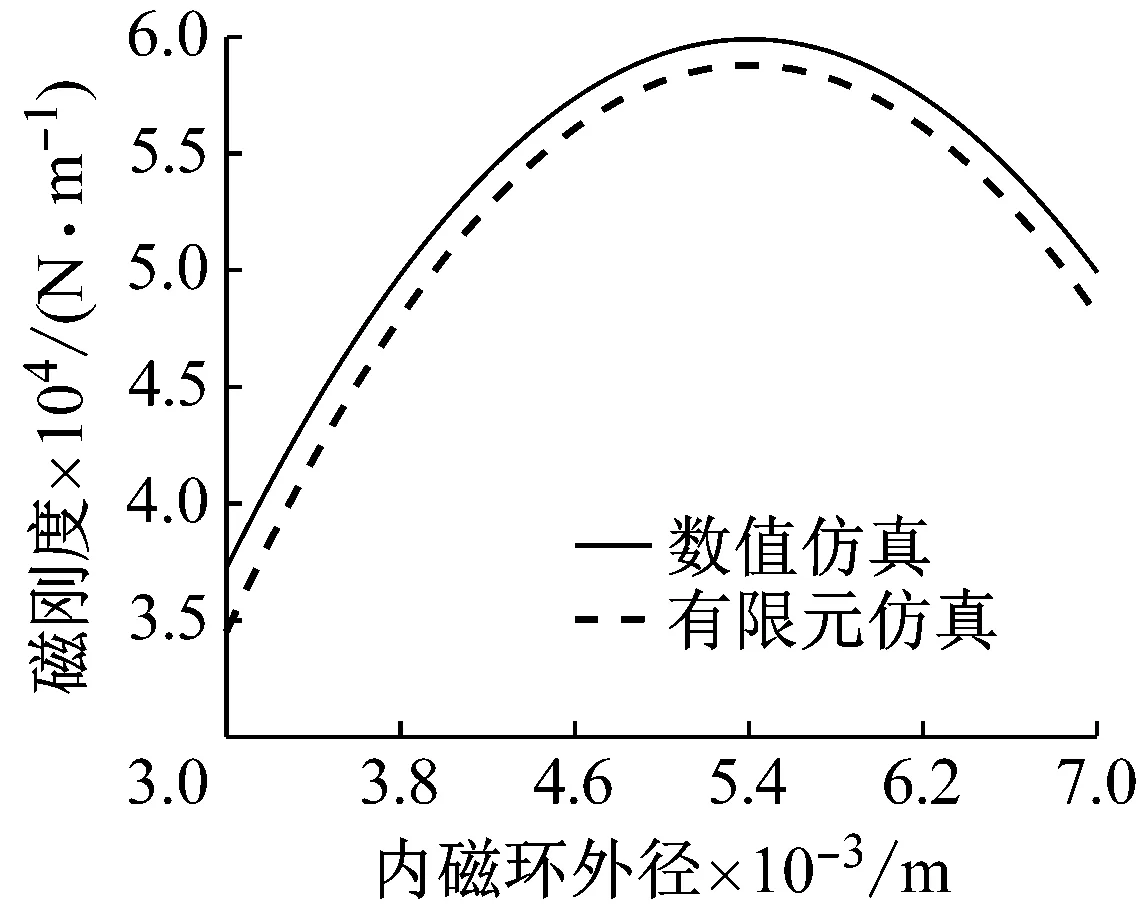
图18 磁刚度随内磁环外径变化的仿真与计算对比曲线
磁刚度随内磁环外径变化的有限元仿真和理论计算结果对比,如表3所示。
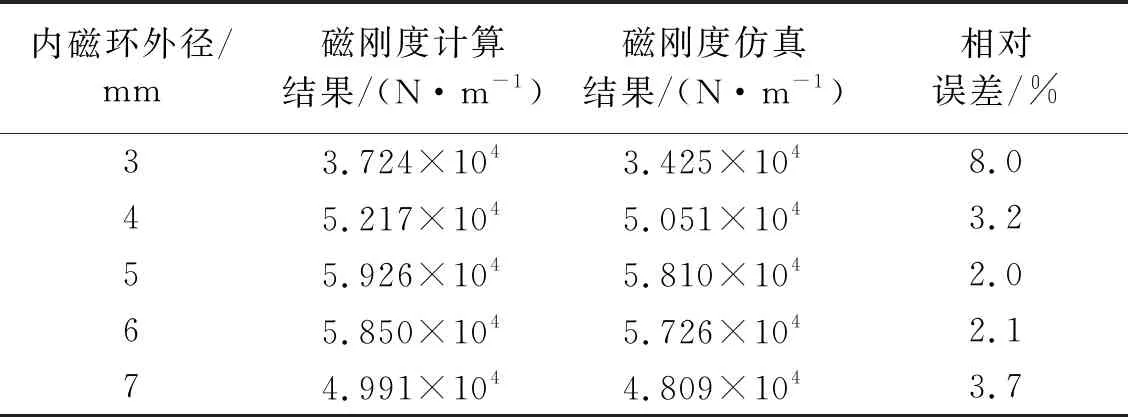
表3 磁刚度随内磁环外径变化的计算结果与仿真结果
设置径向偏移量e为0.15 mm,磁环对轴向间隙x0为2 mm,其他尺寸参数保持不变,以磁环长度L为扫描参数,参数L变化范围为0~5 mm,计算步长为0.1 mm,求出此时磁刚度随磁环长度变化的有限元仿真和理论计算对比曲线,如图19所示。
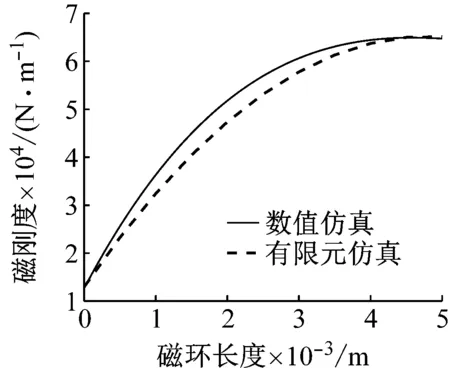
图19 磁刚度随磁环长度变化的仿真与计算对比曲线
磁刚度随磁环长度变化的有限元仿真和理论计算结果对比,如表4所示。
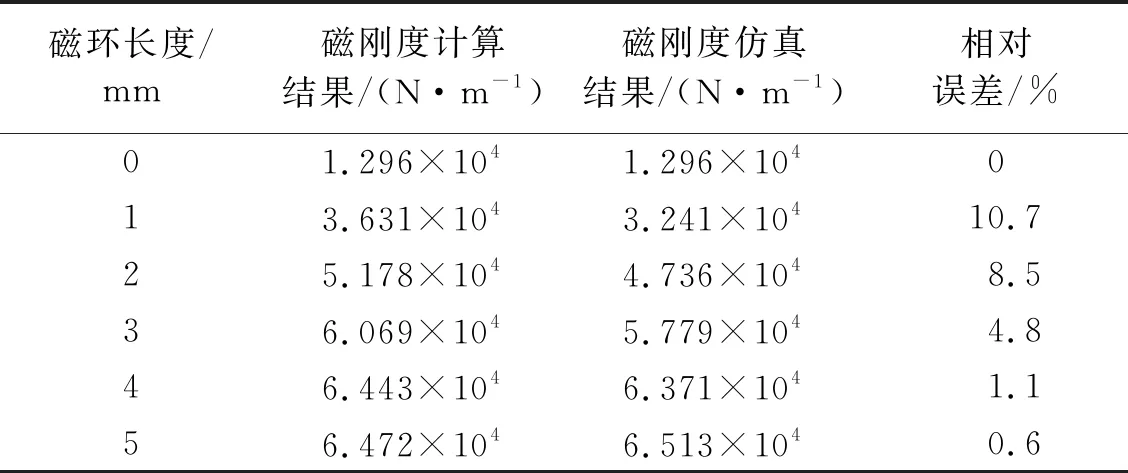
表4 磁刚度随磁环长度变化的计算结果与仿真结果
4.2 电涡流阻尼仿真
利用Maxwell仿真软件中3D瞬态磁场模块对永磁动力减振器中电涡流阻尼进行仿真。根据实际尺寸建立仿真模型,如图20所示。圆柱永磁体长7 mm、半径为5.5 mm、金属片半径为8 mm、金属片厚度为2 mm、金属片和永磁体间隙为0.2 mm,永磁材料设置与磁力仿真中一致。与静磁场仿真不同,电涡流仿真过程中需要设置bond以包含所有运动部件,对金属片添加速度为1 m/s的径向运动。计算域region为100%,分别对计算域、永磁体、金属片和bond添加网格设置,最小网格尺寸分别为5 mm、2 mm、2 mm、2 mm。

图20 电涡流阻尼力有限元仿真模型
以金属片厚度H0为扫描参数,H0变化范围为0~2.5 mm,计算步长为0.1 mm。求出电涡流阻尼随金属片厚度变化的有限元仿真和理论计算对比,如图21所示。
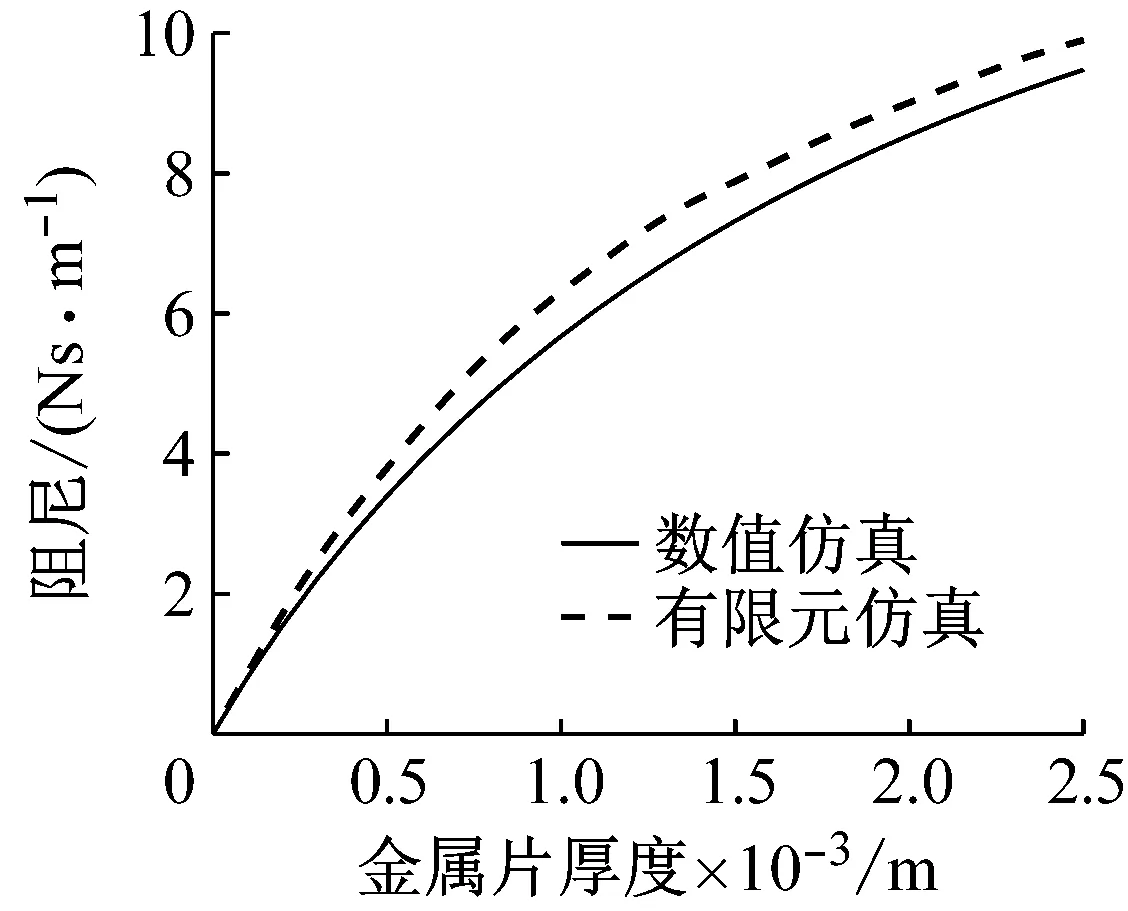
图21 电涡流阻尼随金属片厚度变化的仿真与计算对比曲线
电涡流阻尼随金属片厚度变化的有限元仿真与理论计算结果对比,如表5所示。
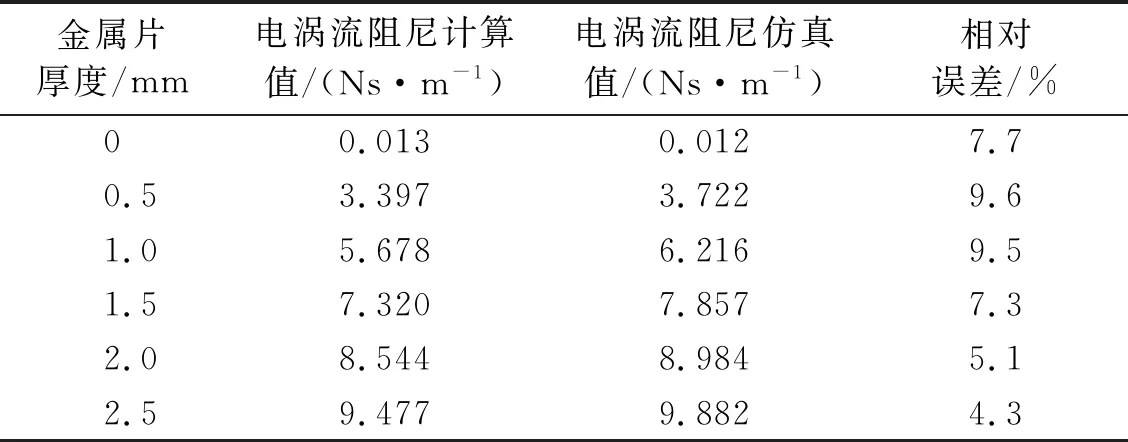
表5 电涡流阻尼随金属片厚度变化的计算结果与仿真结果
设置金属片厚度为2 mm,以金属片和磁环对轴向间隙X0为扫描参数,参数X0变化范围为0~0.5 mm,计算步长为0.1 mm,求出电涡流阻尼随金属片和磁环对轴向间隙变化的有限元仿真和理论计算对比,如图22所示。
电涡流阻尼随金属片和磁环对轴向间隙变化的有限元仿真与理论计算结果对比,如表6所示。
5 动力减振刀杆数值仿真
5.1 动力减振器最优减振条件
针对内置动力减振器的大长径比铣刀,忽略刀杆自身阻尼,可以简化为两自由度有阻尼振动系统[23],如图23所示。图23中:K为刀杆等效刚度;k为动力减振器刚度;x1为刀杆位移;x2为振子位移;c为动力减振器阻尼;F′sinωt为简谐激振力;m为动力减振器振子质量。
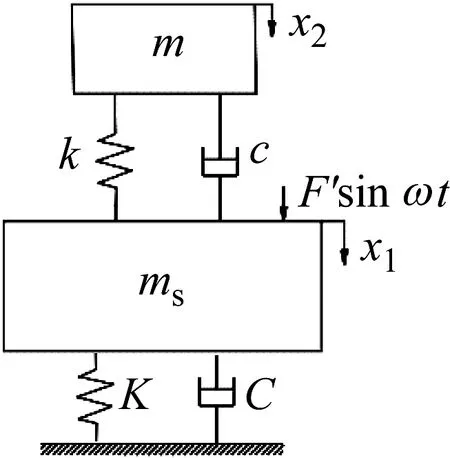
图23 两自由度有阻尼振动系统
传统内置式动力减振器中振子质量越大,刀杆减振效果越好。永磁动力减振器中由于磁刚度和电涡流阻尼会随永磁振子质量变化而变化,因此需要探究质量比和永磁动力减振器最优刚度、最优阻尼之间关系,保证当质量比为某一定值时,磁刚度和电涡流阻尼恰好满足最优刚度和最优阻尼。
针对两自由度有阻尼振动系统,由定点理论可分别求出最优频率比α′和最优阻尼比ξ1[24-25]为
(33)
(34)
动力减振器刚度和阻尼为
k=mωn1
(35)
(36)
式中,ωn1为子系统固有频率。
将式(35)和式(36)分别代入式(33)和式(34)并化简,分别求出动力减振器最优刚度k1和最优阻尼系数c1与刀杆等效刚度K、等效质量ms以及质量比μ之间关系为
(37)
(38)
以长200 mm、直径20 mm、空腔直径16 mm,空腔长50 mm的铣刀为例,刀杆材料为钨钢,弹性模量为320 GPa,密度为15 g/cm3,求出此时铣刀刀杆的等效刚度为1.404×106N/m,等效质量为0.288 7 kg。此时内置动力减振器最优刚度和最优阻尼与质量比之间关系,如图24所示。
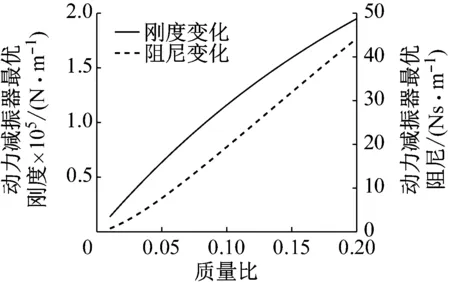
图24 质量比与最优刚度、最优阻尼间关系
通过对永磁动力减振器中磁刚度和电涡流阻尼的计算分析,针对长200 mm、直径20 mm、空腔直径16 mm,空腔长50 mm的铣刀确定永磁动力减振器中各部分尺寸参数,如表7所示。
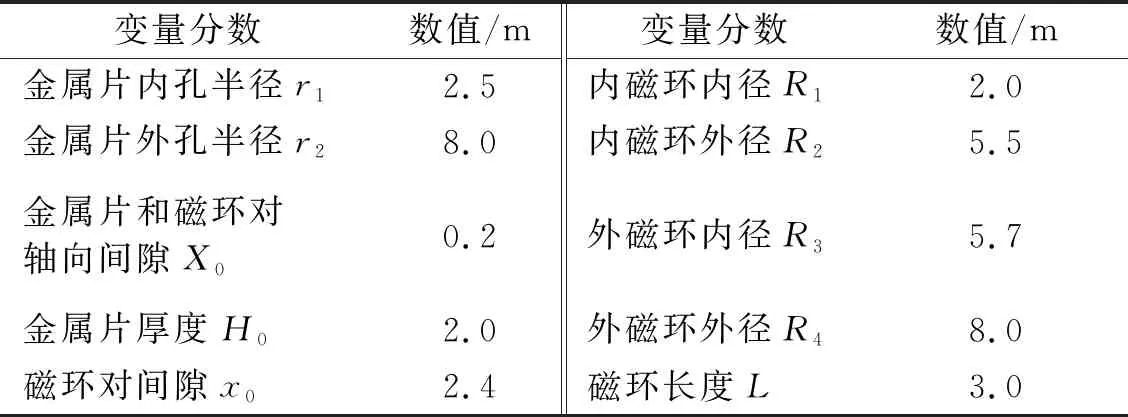
表7 永磁动力减振器尺寸参数
永磁动力减振器中连接杆和永磁材料密度约为7.85 g/cm3,经计算永磁振子质量为0.024 3 kg,此时质量比约为0.085。由图5可知,此时动力减振器所需最优刚度为1.004×105N/m,最优阻尼为15.76。
此刀杆空腔尺寸条件下内置永磁动力减振器包含10组磁环对,经理论计算和电磁仿真求出此结构尺寸下永磁动力减振器提供的磁刚度约为1.008×105N/m,电涡流阻尼约为16.088,满足最优刚度和最优阻尼条件。
5.2 频响幅值对比
针对图23所示的两自由度有阻尼振动系统,建立系统运动微分方程为
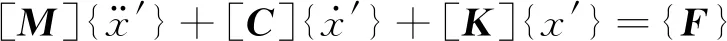
(39)
式中:[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵。
(40)
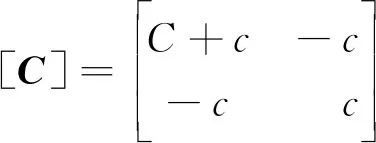
(41)
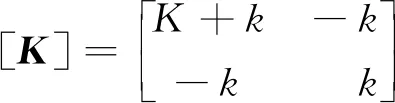
(42)
式中:ms为主系统质量;m为子系统质量;C为主系统阻尼;c为子系统阻尼;K为主系统刚度;k为子系统刚度。
将式(39)由时域转化为频域,可得
(-ω2[M]+jω[C]+[K])|x′(ω)|=[P]
(43)
令
[z(ω)]=-ω2[M]+jω[C]+[K]
(44)
将式(40)代入式(39)可得
|x′(ω)|={z(ω)}-1[P]
(45)
式中:[P]为激振力幅值向量;[z(ω)] 为阻抗矩阵;ω为角频率;x′(ω)为位移x′关于ω的变量。
设刀杆自身阻尼比为0.01,利用MATLAB软件分别对安装永磁动力减振器和不安装永磁动力减振器的铣刀刀杆进行仿真计算,求出频响函数对比,如图25所示。
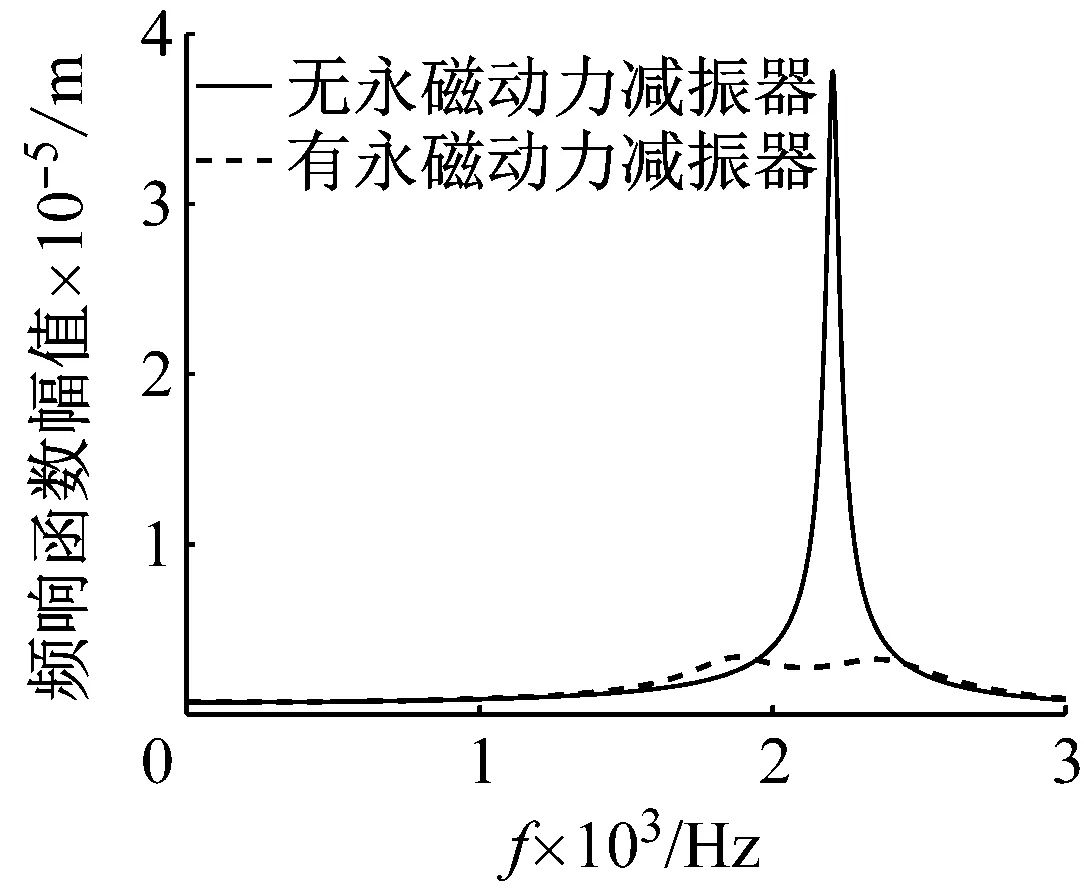
图25 频响函数对比
由图25可知,安装永磁动力减振器后刀杆的频响函数幅值最大值从3.746×10-5m变为3.350×10-6m,下降了91.1%。
6 结 论
本文针对大长径比刀杆设计了一种内置式多层堆叠永磁动力减振器,利用磁刚度和电涡流阻尼提供动力减振器所需刚度和阻尼,解决了传统动力减振器橡胶材料易老化、阻尼液易泄露等问题,实现了刚度和阻尼独立精准的定量设计。建立了多层堆叠式永磁动力减振器中磁力和电涡流阻尼力的理论计算模型,并进行了相关的数值仿真和有限元仿真,得到以下结论:
(1) 永磁动力减振器中径向磁力和径向偏移量之间近似为线性关系,即磁刚度可近似视为定值。动力减振器的磁刚度随内磁环外径的增加先增大后减小,随着磁环长度的增加逐渐增加,随磁环对轴向间隙增加逐渐减小。
(2) 永磁动力减振器中电涡流阻尼随金属片厚度的增加逐渐增加,随金属片和磁环的轴向间隙的增加逐渐减小。
(3) 通过MATLAB软件分别对安装永磁动力减振器前后的铣刀刀杆进行数值仿真,对比两者频响函数变化情况。结果表明,安装永磁动力减振器后频响函数幅值最大值下降91.1%,可以有效抑制刀杆在加工过程中的振动现象。
