具正负系数和多变时滞的高阶非线性中立型差分方程非振动解的存在性
2022-02-21张萍覃桂茳杨甲山
张萍,覃桂茳,杨甲山*
(1.邵阳学院 理学院,湖南 邵阳 422004;2.梧州学院 大数据与软件工程学院,广西 梧州 543002)
0 引言
近年来,随着社会的进步和科学技术的迅猛发展,在数学物理、生物医药、机械工程、自动控制、航天工程及金融等领域提出了大量由差分方程描述的数学模型。因此,学者们对差分方程定性理论(如振动性,非振动解的存在性等)的研究[1-21]兴趣与日俱增,但大多工作集中在方程解的振动性研究[1-5],对方程非振动解的存在性研究较少。本文考虑以下具有正负系数和多变时滞的高阶非线性中立型差分方程:
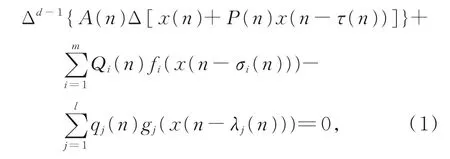
其 中,n≥n0;n0≥0,m≥1,l≥1为 给 定 的 整 数,d≥2为 偶 数;Δ为 向 前 差 分:Δx(n)=x(n+1)-x(n),Δk x(n)=Δ[Δk-1x(n)]。考虑以下条件:
(H1)时滞τ(n),σi(n),λj(n)∈N且均为有界序列(i=1,2,…,m;j=1,2,…,l。下同,略)。
(H2)A(n),P(n),Qi(n),qj(n)均为实数序列,且A(n)≠0,Qi(n)≥0,qj(n)≥0。
(H3)fi(u),gj(u)∈C(R,R),且当u≠0时ufi(u)>0,ugj(u)>0。
(H4)函数fi,gj满足fi(0)=0,gj(0)=0及 局部利普希茨(Lipschitz)条件,即存在常数α>0和Lfi>0,Lgj>0,使得对∀0≤x≤α,0≤y≤α,有

(H5)存在正整数n1≥n0,使得
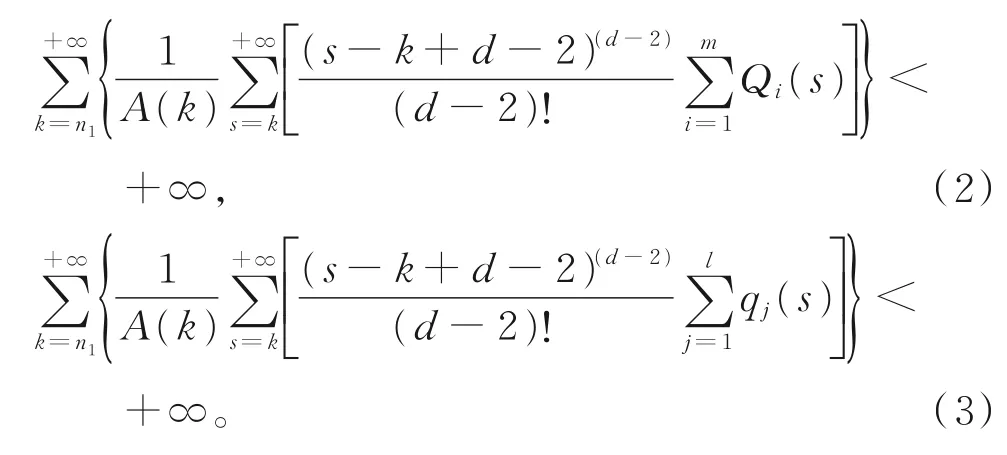
式(1)包含了许多典型的差分方程,如

对于这些典型方程非振动解的存在性,已有一些研究成果。文献[6]研究了具正负系数的常时滞二阶差分方程(E1)非振动解的存在性,在p≥0时,对任意n≥n1及任意常数α>0,均在条件

下得到该方程“一定存在有界的最终正解”的结论;文献[7]研究了具正负系数的常时滞高阶差分方程(E2)非振动解的存在性,但也要求条件(C1)成立;文献[8]虽然改进了文献[7]的条件,未要求条件(C1)成立,但要求中立项系数恒为常数,即P(n)≡p0。
对中立项系数不是常数且方程为多变时滞的情形,文献[9-10]研究了具正负系数的一类二阶差分方程(E3)非振动解的存在性,遗憾的是,其要求“σi≥λj≡λ且至少有一个i使得σi>λ,且 最 终 不 恒为0”,而且没有给出当中立项系数P(n)≤-1时方程(E3)存在有界最终正解的条件;文献[11-12]进一步研究了具正负系数的高阶差分方程(E4)及(E5)的非振动解的存在性,放弃了较为苛刻的条件(C1),得到式(E4)及式(E5)存在有界最终正解的条件,遗憾的是条件
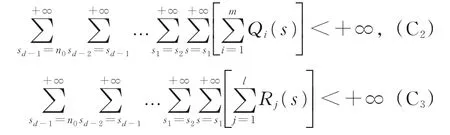
也较强,且式(E4)是单时滞的,而式(E5)又是常时滞的。
综上可知,已有文献对具有正负系数的差分方程正解的存在性研究成果是不完善的。
本文利用Banach空间的不动点原理并结合分析技巧,得到了具正负系数和多变时滞的高阶差分方程(式(1))存在有界最终正解的条件,放弃了以上文献普遍用到的较为苛刻的条件(如条件(C1)或(C2)和(C3)),旨在弥补上述研究的不足,使这些研究结果成为了本文的特例。
1 主要结果及证明
定理1若条件(H1)~(H5)满足,且下列条件之一成立:
(A1)存在正常数p,使得0≤P(n)≤p<1;
(A2)存在常数p0,使得|P(n)|≤p0≤1/3;
(A3)存在负常数p,使得-1<p≤P(n)<0;
(A4)存 在 负 常 数p1,p2,使 得-∞<p1≤P(n)≤p2<-1;
(A5)存在正常数p1,p2,使得1<p1≤P(n)≤p2<+∞;
则式(1)一定存在一个有界的最终正解。
证明为方便,记由于τ(n),σi(n),λj(n)均为有界序列,故记
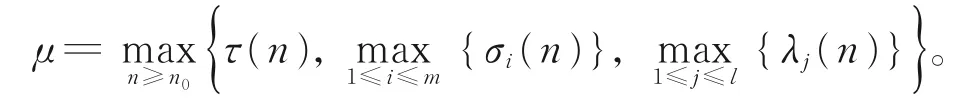
情形A1由式(2)和式(3),可选取充分大的正整 数N1,N1≥max{n1,μ},使 得 当n≥N1时 条 件(A1)成立,并且以下两式也同时成立:
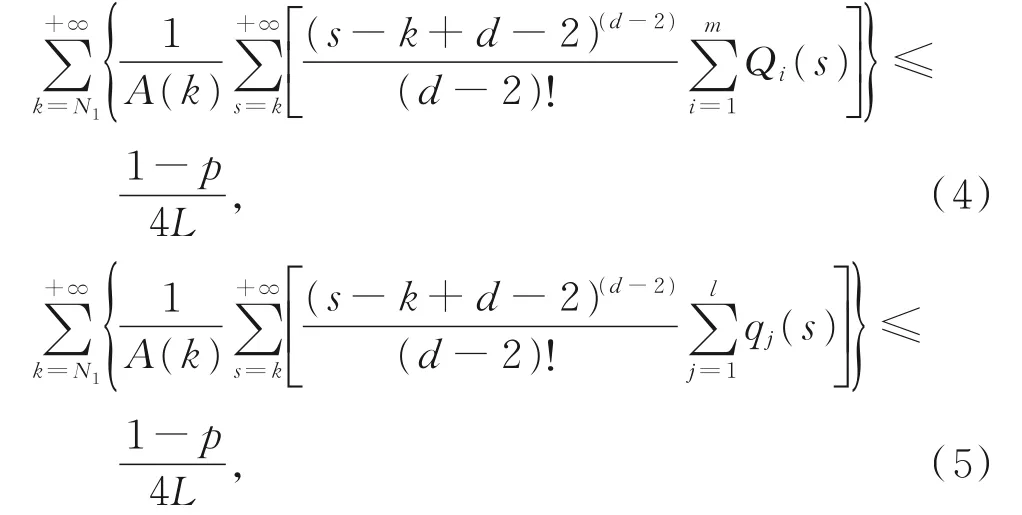
由此可得
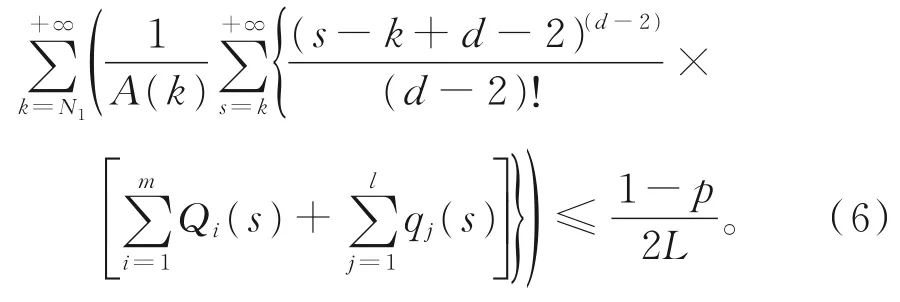
设集合B由所有有界实数序列x=构成,即
B={x=x(n)|x(n)是有界实数,n≥N1-μ},并在B上定义范数:
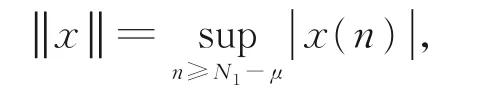
显 然B为Banach空 间。再 记 集 合B1=显然,B1是B的有界闭凸子集。在B1上定义映照T1:B1→B:
易知T1为连续映照。现任取x∈B1,利用条件(H4)及式(4),由式(7)可推得

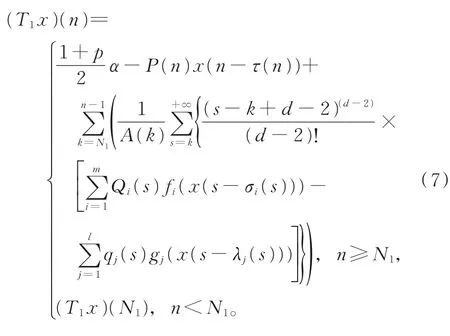
利用条件(H4)及式(5),由式(7)同样可推得

另任取x(1),x(2)∈B1,由式(7)并分别利用条件(H4)及式(6),可推得
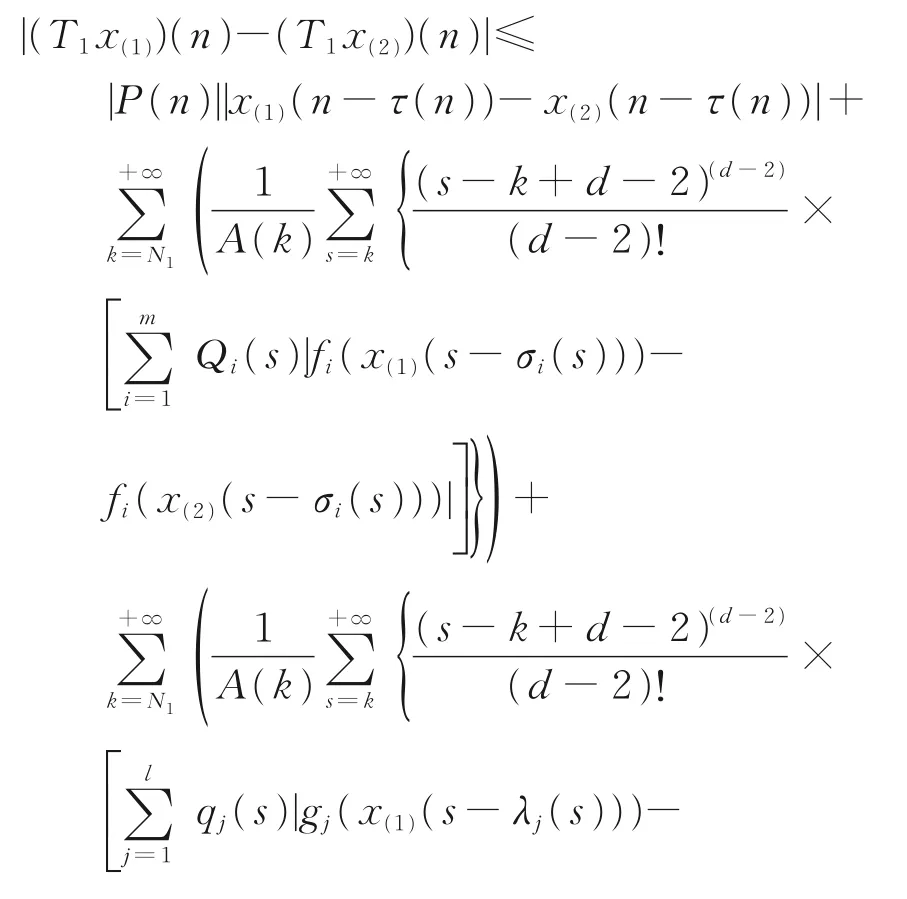

即
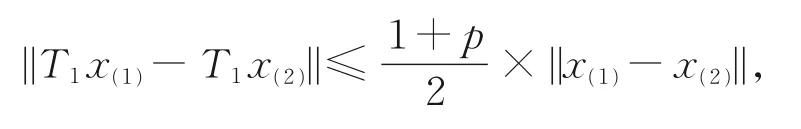
于是由0<p<1可知,T1为 压 缩映照。因 此T1一定有唯一的不动点x∈B1,使得T1x=x。再由B1的定义及式(7),知此不动点是有界的,并且最终满足
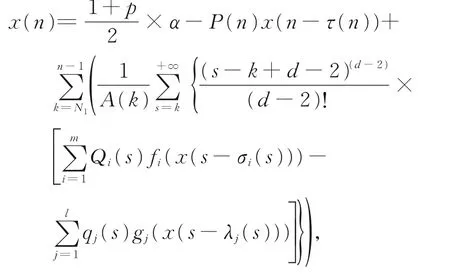
移项,然后求一次差分,可得

式(8)两边同乘A(n)后再求一次差分,并由式(9)可得

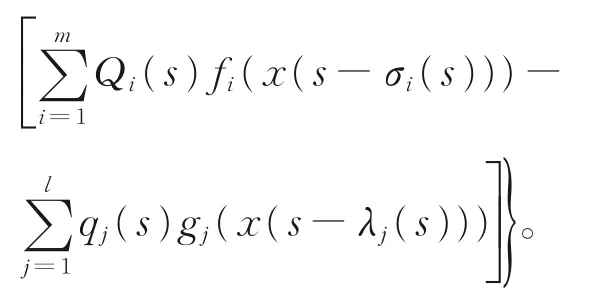
一般地,有

这 里N(0)=1,k=2,3,…,d-1。注 意 到d是 偶数,所以有

对上式再求一次差分,得
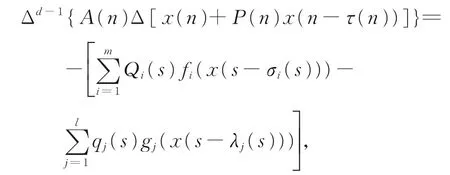
即
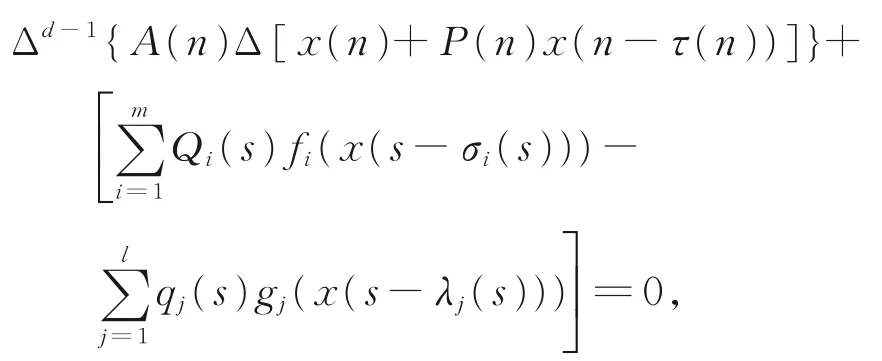
说明该不动点{x(n)}是式(1)的一个有界的最终正解。
情形A2存在常数p0,使得|P(n)|≤p0≤1/3。由式(2)和式(3),可选取充分大的正整数N2,N2≥max{n1,μ},使得下列两式同时成立:
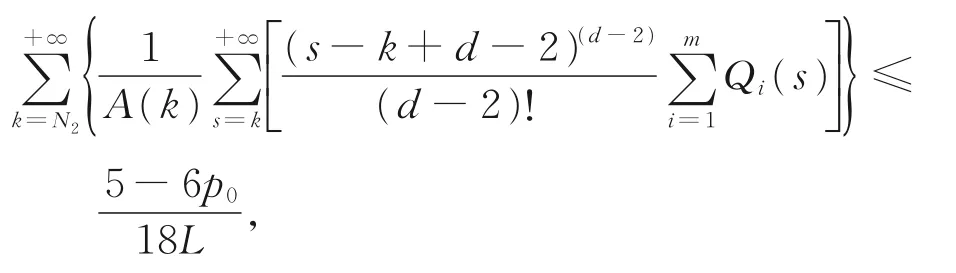
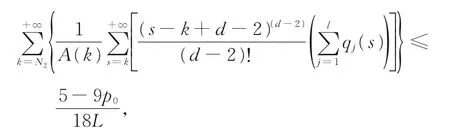
于是有
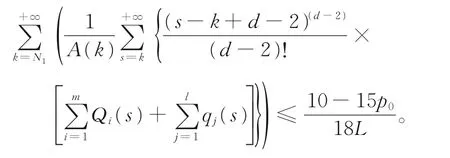
令B={x=x(n)|x(n)是有界的实数,n≥N2-μ},

定义映照T2:B2→B:

类似于情形A1,分别有
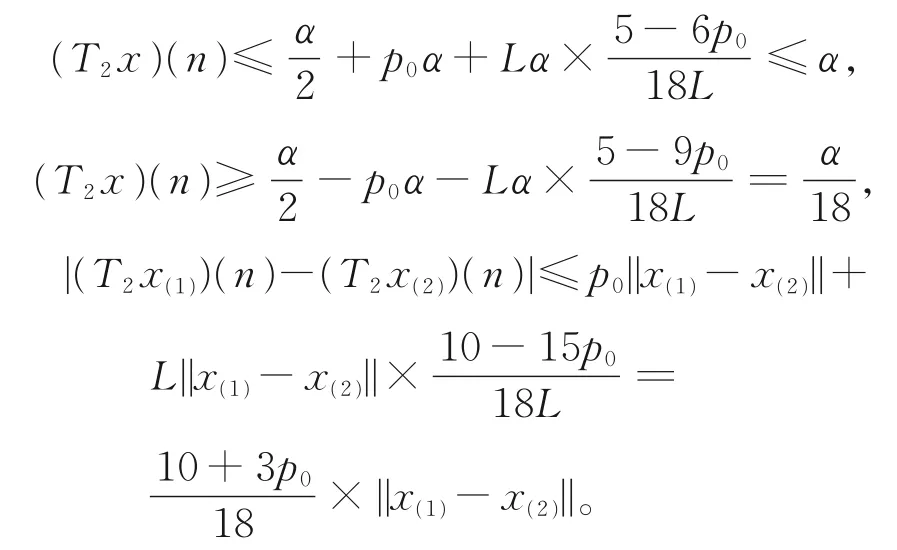
其余证明类似于情形A1,所以在情形A2下,式(1)也有一个有界的最终正解。
情 形A3存在 负 常数p,使 得-1<p≤P(n)<0。由式(2)和式(3),可选取充分大的正整数N3,N3>max{n1,μ},使得下列两式同时成立:


于是有
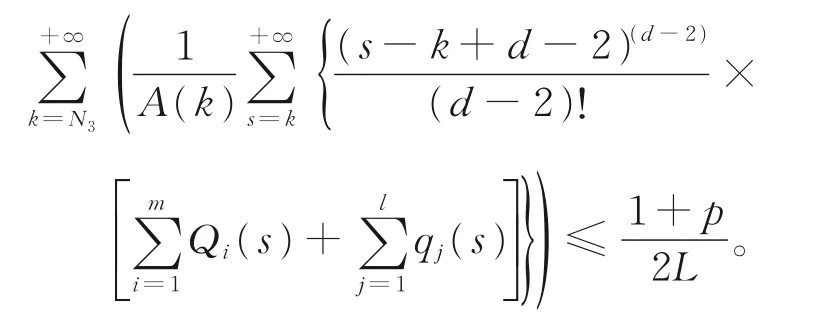
令B={x=x(n)|x(n)是有界的实数,n≥N3-μ},
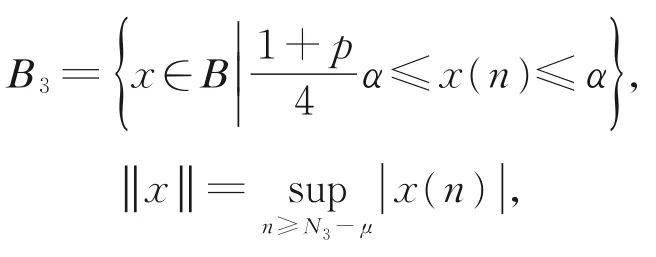
定义映照T3:B3→B:
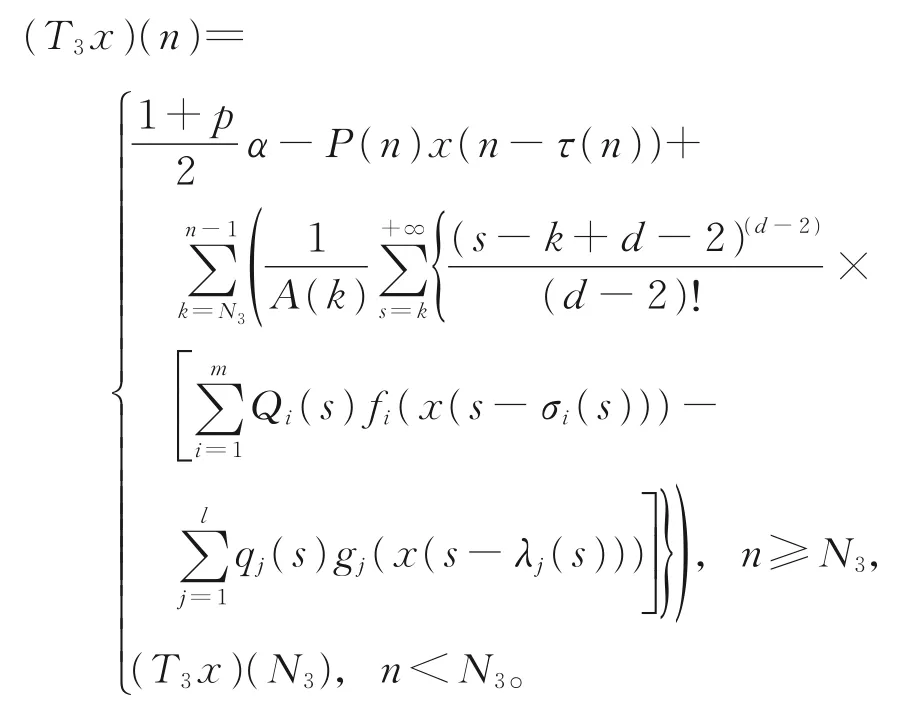
其余证明完全类似于情形A1,此证略。
情形A4存在负常数p1,p2,使得-∞<p1≤P(n)≤p2<-1。由式(2)和式(3),选取充分大的正 整 数N4,N4>max{n1,μ},使 得 下 列 两 式 同 时成立:
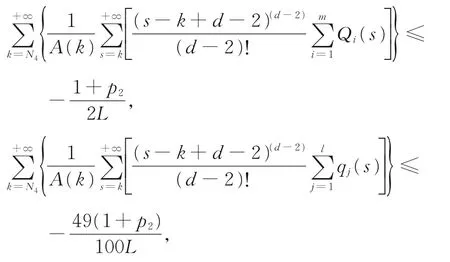
于是有
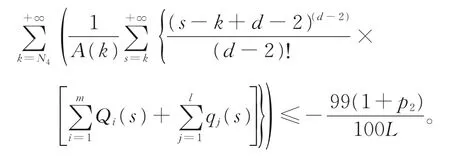
令B={x=x(n)|x(n)是有界的实数,n≥N4-μ},

定义映照T4:B4→B:
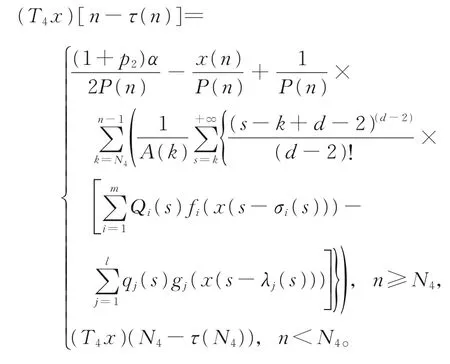
其余证明完全类似于情形A1,此证略。
情 形A5存 在 正 常 数p1,p2,,使 得1<p1≤P(n)≤p2<+∞。由式(2)和式(3),可选取充分大的正整数N5,N5>max{n1,μ},使得下列两式同时成立:

于是有
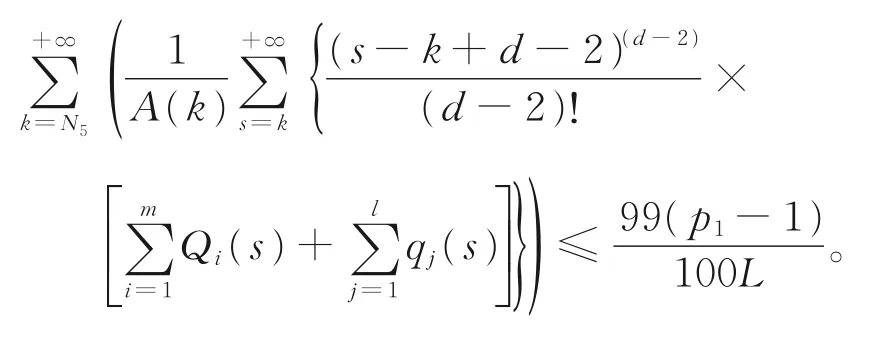
令B={x=x(n)|x(n)是有界的实数,n≥N5-μ},
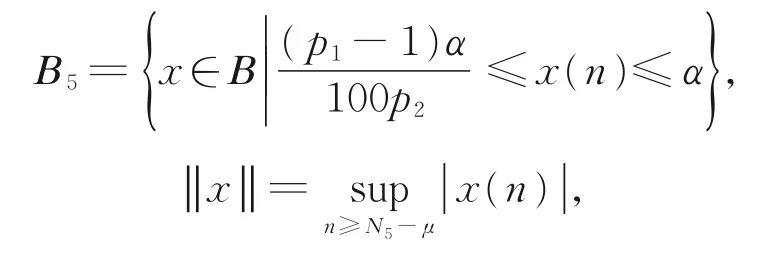
定义映照T5:B5→B:

其余证明完全类似于情形A1,此证略。
定理1证毕。
注1当d≥2且为奇数时,用完全类似的方法可以证明定理1的结论也成立。如对情形A1,只需将映照T1:B1→B修改为
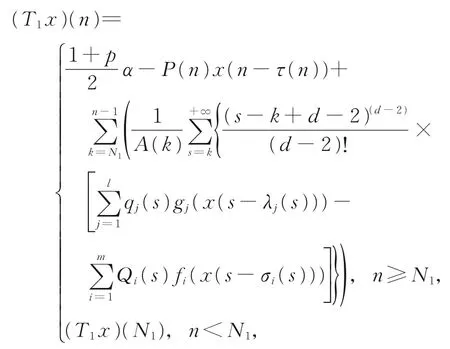
其余部分证明完全相同。
注2对 二 阶 方 程,若 式(1)中,d=2,A(n)≡1,P(n)≡p0,m=1,l=1,f(x)=x,g(x)=x,并且τ(n)≡τ0,σ(n)≡σ0,λ(n)≡λ0,则由定理1的情形A1、情形A5,便可得到文献[6]中的所有定理,但本文放弃了文献[6]中对任意n≥n1均有αQ(n)-R(n)≥0的条件,而且还给出了其他情形的结果。此外,文献[9-10]的结果显然也是本文的特例,但本文的条件更为宽松,并且给出了P(n)≤-1的结果。
注3对高阶方程,若式(1)中,A(n)≡1,m=1,l=1,f(x)=x,g(x)=x,并且τ(n)≡τ0,σ(n)≡σ0,λ(n)≡λ0,则由定理1便可得到文献[7]中的所有结果,但本文放弃了文献[7]中对任意n≥n1均 有αQ(n)-R(n)≥0的 条 件。进 一 步,若P(n)≡p0,则由定理1便可得到文献[8]的定理6~定理9,但本文增加了中立项系数P(n)在0附近振荡的情形,即|P(n)|≤1/3时的结果。此外,文献[11-12]的结果显然也是本文的特例,但本文定理中的条件较文献[11-12]的条件(C2)和(C3)更宽松。因此,本文定理推广并改进了已有文献的相关结论。
注4当中立项系数P(n)在±1附近振荡时,情况较为复杂,此时式(1)是否存在有界的最终正解,有待进一步研究。
