一类群体平衡方程的尺度变换群分析及显式精确解

林府标，张千宏

（贵州财经大学 数统学院，贵州 贵阳 550025）

0 引言

群体平衡方程是描述具有特殊特征的离散实体系统模型的连续型方程，这些实体包括粒子、晶体、乳剂、液滴、泡沫、种群等；同时包含纯偏微分方程、积分方程、代数方程等，通常分别用粒子的种群密度分布函数、增长率或破损率表示种群平衡、粒子质量。群体平衡方程应用领域广泛，但鉴于在实际工程领域中缺乏解析解，其研究途径几乎只能借助于数值技术［1-4］。粒子可用尺寸、形状、液体和气体的空隙、成分、年龄、质量和体积等表征，其尺寸、质量、体积是研究粒子密度分布基本的内部变量坐标［1-4］。矿石或其他固体材料的破碎、粉碎、尺寸减缩等是粒子的破损过程；细菌种群的繁殖、生长、死亡、分裂等为粒子的生长过程。在描述化学过程、微粒系统时，可将既有生长过程又有破损过程的连续型群体平衡方程［3］写为

其中，t表示时间；x表示粒子的尺寸（质量、体积），f(x，t)表示尺寸（质量、体积）为x的粒子在t时刻的种群密度分布函数；G(x，t)表示尺寸（质量、体积）为x的粒子在t时刻的增长率；v(x，t)表示尺寸（质量、体积）为x的粒子的破损平均数；假设粒子的破损是相互独立的，b(x，t)表示尺寸（质量、体积）为x的粒子在t时刻的破损率，即单位时间内正在破损的粒子数，一般情况下，破损率系数b(x，t)随x的增大而增大，例 如，幂 函 数 型 破 损 率b(x，t)=kxγ，k＞0，γ＞0；p(x|y)表示尺寸（质量、体积）为y的粒子分解或破损为尺寸（质量、体积）为x的粒子的概率，与时间相互独立，概率函数p(x|y)满足规范性条件：

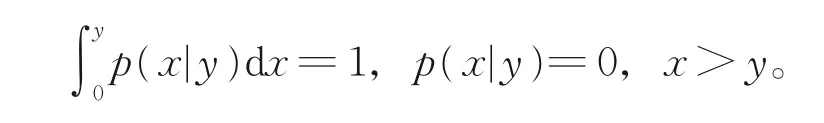
假设f(x，t)是积分-偏微分方程（1）的任意解，则该精确解满足尺寸（质量、体积）足够大的粒子，相应种群密度分布函数f(x，t)必然为零［1-3］，特别地，当满足性质f(∞，t)=f(x→∞，t)=0时，正则性条件为G(∞，t)f(∞，t)=0，对应的边界条件和柯西问题的初始条件分别为

在工程应用领域，常用平均数或总数研究粒子的行为分布及相关性质。其中，总体平衡（TB）、零阶矩M0(t)和一阶矩M1(t)的定义分别为

其中，零阶矩M0(t)表示单位体积粒子的平均质量，一阶矩M1(t)表示单位体积粒子的总质量。

齐次增长率函数和破损率函数相对容易处理，即对任意的λ存在幂指数p≥0，γ≥0，使得增长率系 数G(x，t)和 破 损 率 系 数b(x，t)分 别 满 足 齐 次方程

假设粒子破损的平均数是双重的，增长率函数和破损率函数均不依赖于时间而仅取决于粒子的尺寸（质量、体积），注意到假设条件概率函数与时间的相互独立性和规范性，进一步选取

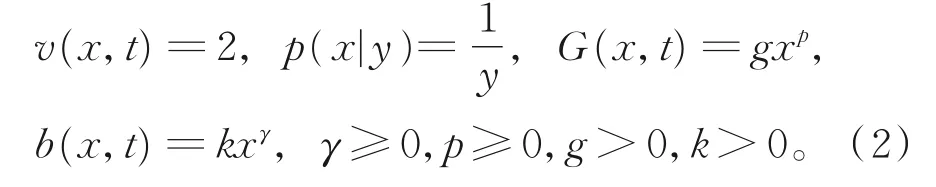
于是，幂函数型增长率和破损率的群体平衡方程（1）在约束条件（2）下可简化为

在日常生活和工业生产中，最大的困难不是如何建立一个实体微粒过程模型，而是除数值技术［1-4］外无其他精确求解满足实际问题的群体平衡方程的途径。因此，为精确描述、解释、理解和应用这些实体模型，探求满足边界条件和初值条件的精确解是有实际价值和意义的。

群体平衡方程的主要求解方法可粗略地分为数值方法和矩方法［1-4］。而经典的李群分析法［5］无法直接用于求解积分-偏微分方程（1）。改进的李群分析法［6-7］在许多交叉学科领域已有应用，特别是已用于求解积分-偏微分方程、时滞微分方程和随机微分方程［8-15］，其最大困难是求解积分-偏微分方程的决定方程，由于决定方程仍为积分-偏微分方程，其解法依赖于原积分-偏微分方程的结构、性质和特征等［8-15］。采用改进的李群分析法求解式（3），最大困难是决定方程及其求解方法，因式（3）中，局部强非线性项为变下限积分类型。相反，采用尺度变换群分析法［6，8］因不需要求解复杂的积分-偏微分方程的决定方程，求解新的积分-偏微分方程的部分对称、群不变解和显式精确解常常是简洁且行之有效的。

本文采用尺度变换群分析法、观察法和试探函数法求式（3）的精确解。重点求满足实际问题的有意义的真实显式精确解，分析和探讨这些显式精确解所满足的边界条件和柯西问题的初始条件，以及解的动力学特性，并能验证数值解的正确性和精度，为工程应用领域提供理论参考，丰富群体平衡方程的理论内容。

1 尺度变换群分析法

采用尺度变换群分析法［6，8］求式（3）所接受的李群，考虑尺度变换群

其中，a为群参数，及式（3）的相应变换方程

由尺度变换群分析法的理论算法和式（4），可假设式（3）所接受的无穷小李对称算子为

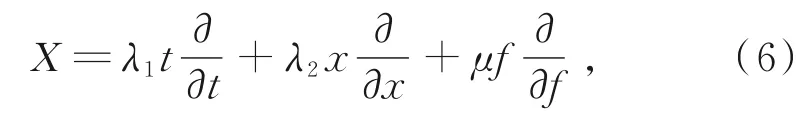
其中，λ1，λ2，μ均为实参数。为分析和研究式（4）如何将式（5）的解变换为式（3）的解f=f(x，t)，进一步将式（4）的逆变换群改写为

将式（4）和式（7）代入式（5），化简得

注意到f(x，t)是式（3）的任意解，尺度变换群作用式（3）不变，由式（8），实参数λ1，λ2满足的不变量约束条件为

由式（2）和式（9），得到增长率和破损率函数分别为

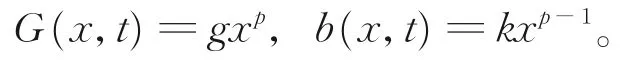
于是，式（3）变为

考虑单参数平移变换李群

其中，τ0为群实参数。类似于上述分析和计算，可证明平移变换李群Tτ0作用式（3）不变，因此，式（3）接受平移变换李群Tτ0，其对应的无穷小李对称平移算子为

鉴于实参数λ1，λ2，μ的任意性，结合式（9）和平移变换李群Tτ0以及无穷小算子式（6），得到式（10）所接受的无穷小李对称算子为

定理1设由式（10）接受的所有无穷小李对称算子构成的李代数为L，则L3=span{X，Y，Z}构成实数域上L的3维子李代数。

由文献［16］，得到3维子李代数L3的换位子运算结果，见表1。

表1 子李代数L3的换位子运算结果Table 1 Commutator table of Lie subalgebra L3

由表1可得，内自同构

求解相应的李方程，得

由内自同构Ai(i=1，2)对应的李变换群和理论算法［6-7］，可得3维子李代数L3的最优化系统，见表2，其中，α为任意实数。

表2 子李代数L3的最优化系统Table 2 Optimal system of Lie subalgebra L3

2 群不变解和显式精确解

情形1span{Y+αZ}，p≠1，α∈R。

无穷 小 李 对 称 算 子Y+αZ，p≠1，α∈R的群不变量为由平移算子X，可假设式（10）的显式精确解为

其中，函数φ(z)满足约化积分-常微分方程

情形2span{Y+αZ}，p=1，α∈R。

无穷 小 李 对 称 算 子Y+αZ，p=1，α∈R的群不变量为t，x-α f。于是，假设式（10）的显式精确解为f(x，t)=xαφ(t)，α＜0，其中，函数φ(t)满足约化可分离变量的常微分方程φ′=-βφ，其通解为φ(t)=cexp(-βt)。由平移算子X，可得式（10）的显式精确解为

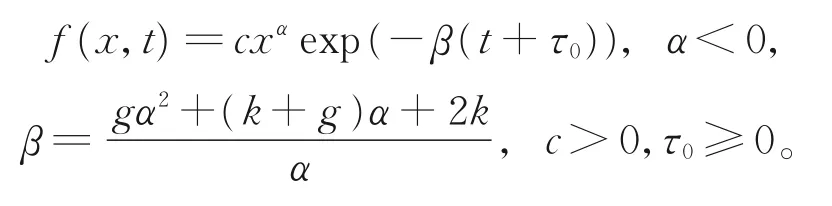
注意到当x→∞时，此精确解满足f(x，t)→0，即满足条件f(∞，t)=0。在破损系数为常数的粒子系统中，当线性增长的粒子尺寸（质量、体积）足够大时，种群密度分布函数f(x，t)必然为零。边界条件和柯西问题的初始条件分别为

情形3

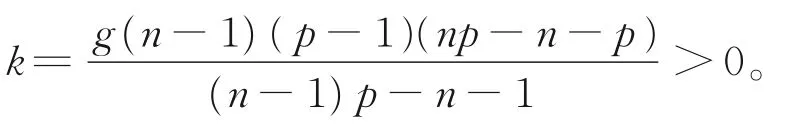
用试探函数法，可得式（13）的显式精确解

结合平移算子X和式（12），得式（10）的显式精确解

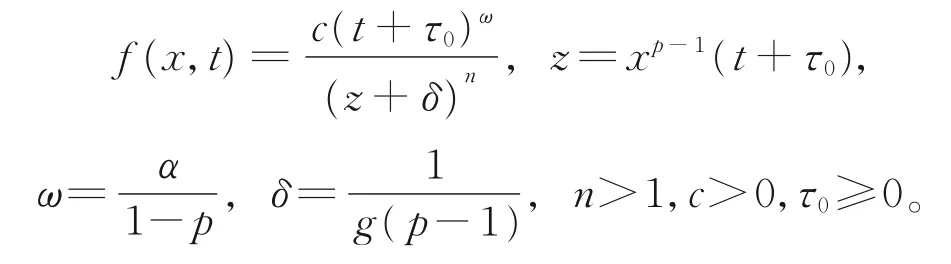
若p＞1，当粒子尺寸x→∞时，精确解满足f(x，t)→0，即满足条件f(∞，t)=0。表明既存在增长又存在破损的粒子过程，当粒子尺寸（质量、体积）足够大时，种群密度分布函数f(x，t)必然为零。当系统中无粒子时，增长率满足G(0，t)=0。显式精确解f(x，t)对应的边界条件、柯西问题的初始条件、总体平衡（TB）分别为

在破损过程中，粒子的平均质量和总质量依赖参数n，p的选取和零阶矩M0(t)及一阶矩M1(t)。若p=2，则零阶矩M0(t)和一阶矩M1(t)分别为

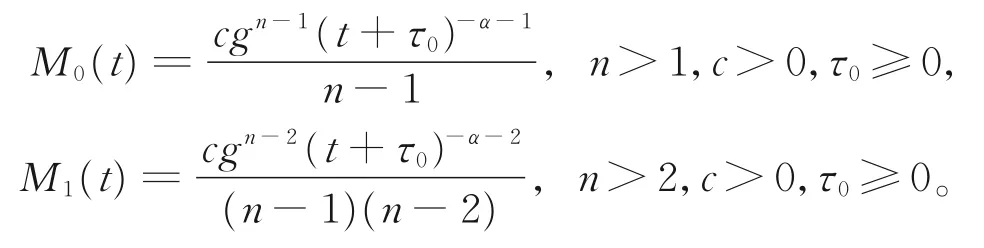
为行文简洁，以下情形不再讨论和分析精确解所对应的边界条件和初值条件以及零阶矩M0(t)和一阶矩M1(t)。

情形4n＞1，p≠1，α=n(1-p)，

用试探函数法，可得式（13）的显式精确解为

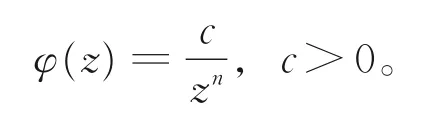
由式（12）和平移算子X，得式（10）的显式精确解为

情形5p=3，k=6g。

用试探函数法，可得式（13）的显式精确解为

由平移算子X和式（12），得式（10）的显式精确解为

情形6

类似地，用试探函数法探究式（13）的显式精确解，由式（12）和平移算子X，可得式（10）的显式精确解为

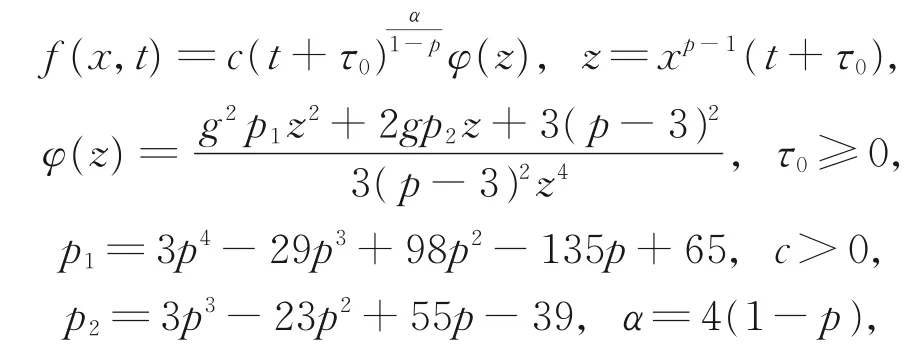
函数φ(z)为式（13）的解。

情形7G(x，t)=gxp，b(x，t)=kxp-1。

用观察法和试探函数法，得式（10）的显式精确解为

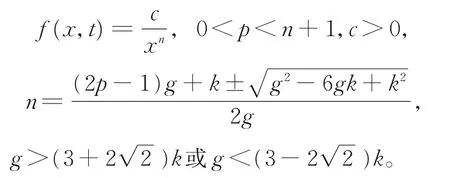
情形8

用试探函数法，得式（13）的显式精确解为

由式（12）和平移算子X，得式（10）的显式精确解为

情形9span{X+Z}。

无穷小李对称算子X+Z的群不变量为x，exp(-t)f。由平移算子X，可假设式（10）的显式精确解为

其中，函数φ(x)满足约化积分-常微分方程：

情形10span{X-Z}。

无穷小李对称算子X-Z的群不变量为x，exp(t)f。由平移算子X，可假设式（10）的显式精确解为

其中，函数φ(x)满足约化积分-常微分方程：

情形11span{X}。

无穷小李对称算子X的群不变量为x，f，可假设式（10）的显式精确解为

其中，函数φ(x)满足约化积分-常微分方程：

3 结论

将尺度变换群分析法成功地应用于带有变下限强非线性积分项的群体平衡方程。结合观察法和试探函数法，得到了存在齐次增长率和破损率的群体平衡方程的部分对称、群不变解和显式精确解。分析了部分显式精确解对应的边界条件、柯西问题的初值条件以及零阶矩和一阶矩。所得显式精确解可验证数值解的正确性和精确度。