一种永磁同步电机声品质主观评价方法研究

王 博，王海文，江祖毅，胡 溧，龚海清

（1.武汉科技大学汽车与交通工程学院，武汉430065；2.博格华纳汽车零部件（武汉）有限公司工程中心，武汉430100）

在当前汽车领域，纯电动汽车发展速度与规模正成逐年上升趋势，其中永磁同步电机因其弱磁性能好、输出功率大、输出效率高和输出稳定的优势，在电驱动系统中被广泛应用。由于永磁同步驱动电机是电动汽车的重要组成部分，其噪声水平直接影响到车内噪声质量，进一步对汽车竞争力产生重要影响。要想抑制电动汽车车内噪声，优化车内噪声声品质，必须对电机噪声特性有所了解。对电机噪声声品质的分析预测和研究成为新能源汽车发展的关键点。

王永超等以4辆不同类型的纯电动汽车在匀速和缓油门加速工况下电机近场合驾驶员右耳旁噪声采集样本为评价对象，分析了电磁噪声对电动汽车声品质的影响。邱子桢等对稳态工况下电动汽车驱动永磁同步电机的主观声品质预测模型进行研究，利用多元线性回归法，建立了声品质主客观预测模型。左言言等以某款混合动力汽车为研究对象，针对其非稳态工况下的噪声声品质进行研究，基于最小二乘支持向量机算法，建立了声品质评价预测模型。莫愁等采用成对比较法对某混合动力汽车进行主观声品质评价，采用回归分析法和神经模糊逻辑算法建立了主观烦扰度预测模型和声品质等级评价标准。

本文以某型10 极60 槽永磁同步电机为研究对象，利用Bradley-Terry 数学模型对主观评价的条件概率似然度进行最大似然估计，在先验概率的基础上求解出声品质评价结果的最大似然估计值，得到可对声品质定量描述的选择偏好度值，并将该值作为因变量参与声品质预测模型的搭建。以径向基函数（Radical Basis Fuction，RBF）神经网络为非线性逼近函数，通过多种群遗传算法（Multi-Population Genetic Algorithm，MPGA）优化RBF 神经网络，建立基于MPGA-RBF 神经网络的永磁同步电机声品质主观评价预测模型，再通过预留样本对模型进行检验，发现该模型性能稳定，泛化能力强，预测精度高，可以有效地对永磁同步电机声品质进行预测评价。

1 Bradley-Terry模型简介

设有个体集合｛，…，x｝，其中个体x(= 1，…，)在某方面的能力参数值为γ，令Y表示集合个体x与x相互比较的结果，当个体x优于（或 不 小 于） x时， 有Y=1， 反 之Y=0。 记(Y= 1)为x优于x的概率，(Y= 0)为x小于x的概率，则

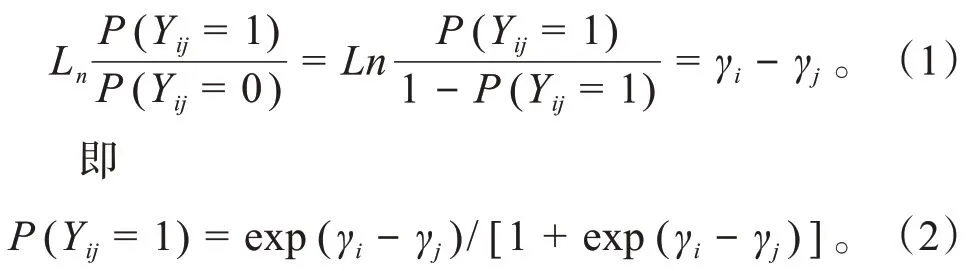
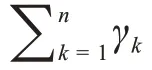
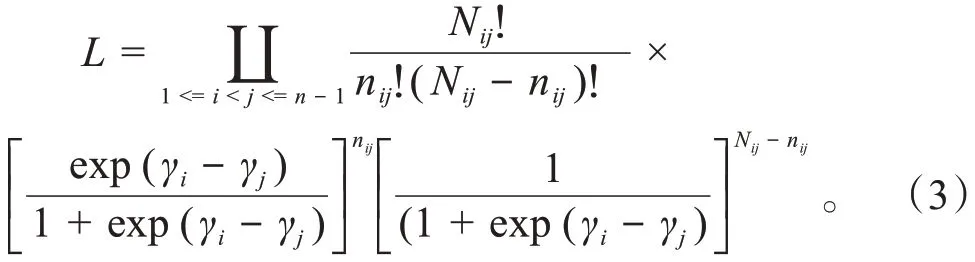
通过最大似然估计法对式（3）进行处理求解，先对式（3）取对数化简，如式（4）所示。

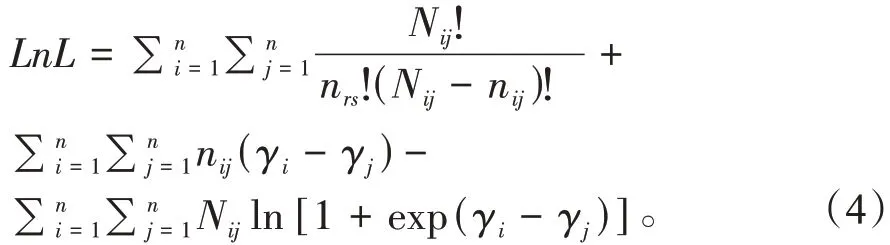
对式（4）通过最大似然法化简得到矩阵：

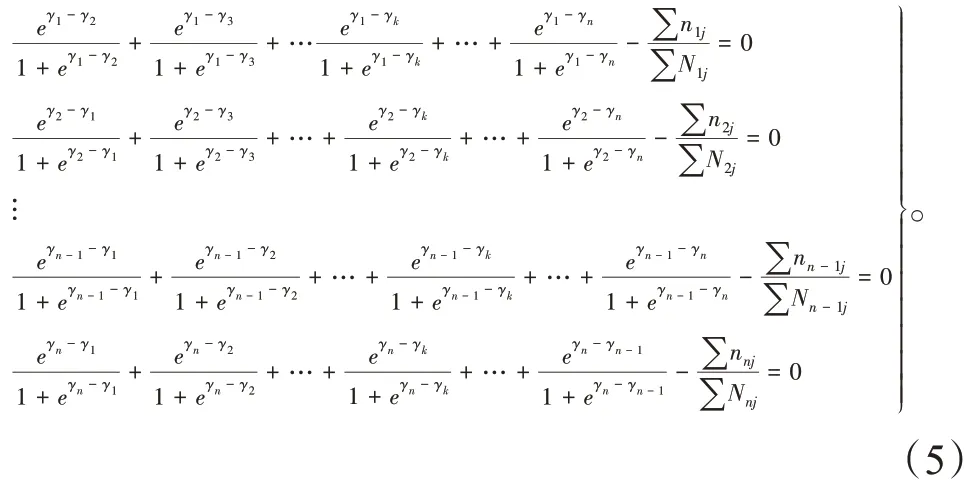
求解方程组即可以得出每个个体的能力参数值｛γ｝。

2 永磁同步电机噪声采集与处理

以某型10极60槽永磁同步电机为试验对象，通过电机测试台架模拟各种工况，试验主要设备见表1。

表1 试验仪器设备

为了降低背景噪声的影响，试验在封闭隔声的房间内进行，并且尽可能减少外部干扰。根据GB/T 6882—2016和GB/T10069.1—2006在电机测试控制台架所能提供的最大安全转速条件下，确定出的测试电机稳定转速测试范围为1 000 r/min、2 000 r/min、3 000 r/min、4 000 r/min、5 000 r/min和6 000 r/min，电机转矩测试范围为35 Nm、70 Nm、105 Nm、130 Nm，共计24个稳态工况。

在LMS.Test.Lab 声振测试系统下，通过LMS SCADAS Mobile 16 通道数据采集前端，利用GRAS 声压传感器对噪声进行采集。噪声样本采样率为12 500 Hz，频率分辨率为1 Hz，采样时长为30 s，每个工况信号采集3次，测点布置遵循5点测试法，测距为距离电机外壳30 cm 处，采用近场测试。试验台架布置如图1所示。

图1 噪声测试试验布置

去除受到干扰的样本噪声，为了避免噪声样本时间过长引起听觉疲劳，导致评价精确度下降，将用于主观评价的样本信号时长截取为4 s。使用音频编译软件将噪声样本两两结合，以便利用成对比较法进行主观评价试验。为了降低样本间后掩蔽效应，在样本A 后面插入2 s 静音。处理后的成对比较样本信号如图2所示。

图2 成对比较样本

3 永磁同步电机声品质主观评价

评审团共招募了23 名年龄在20～32 岁听力正常并具有一定声品质主观评价经验的学生，其中有19 名男性以及4 名女性，通过听力培训使评审团成员熟悉评价流程。

3.1 基于Bradley-Terry算法优化成对比较法

采用分组成对比较法进行声品质主观评价试验，将经过模型计算得到的声品质舒适度感知能力参数值作为改进的主观评价值。为保证评价结果的稳定性，需要审核评价数据，使用Spearman 相关分析法，如式（6）所示，对每个评价者进行相关分析，剔除不稳定的评价结果。

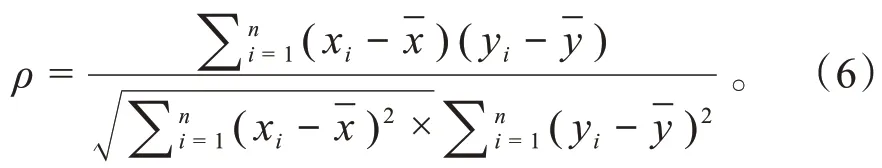
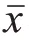
然后，计算每一个样本与其它样本之间相关系数的平均值，结果见表2。

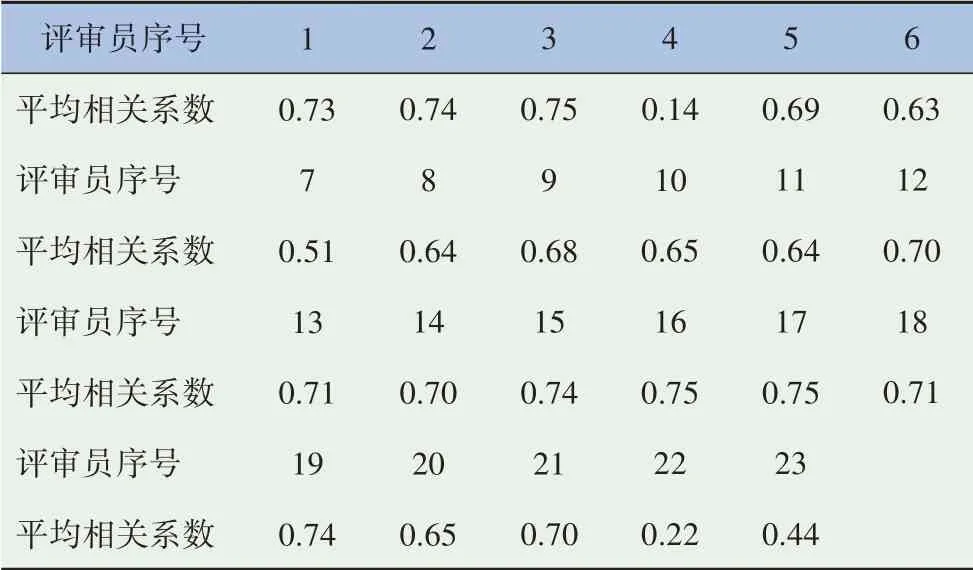
表2 样本间平均相关系数

由表2 可知，4 号、7 号、22 号、23 号评审员的平均相关系数小于0.6，呈现低相关。剔除这4个评价主体。为计算Bradley-Terry模型，对剩余19个评价主体的所有评价样本的序关系频数表进行加总降维。对单一评价主体加总降维后得到的平均总体见表3。

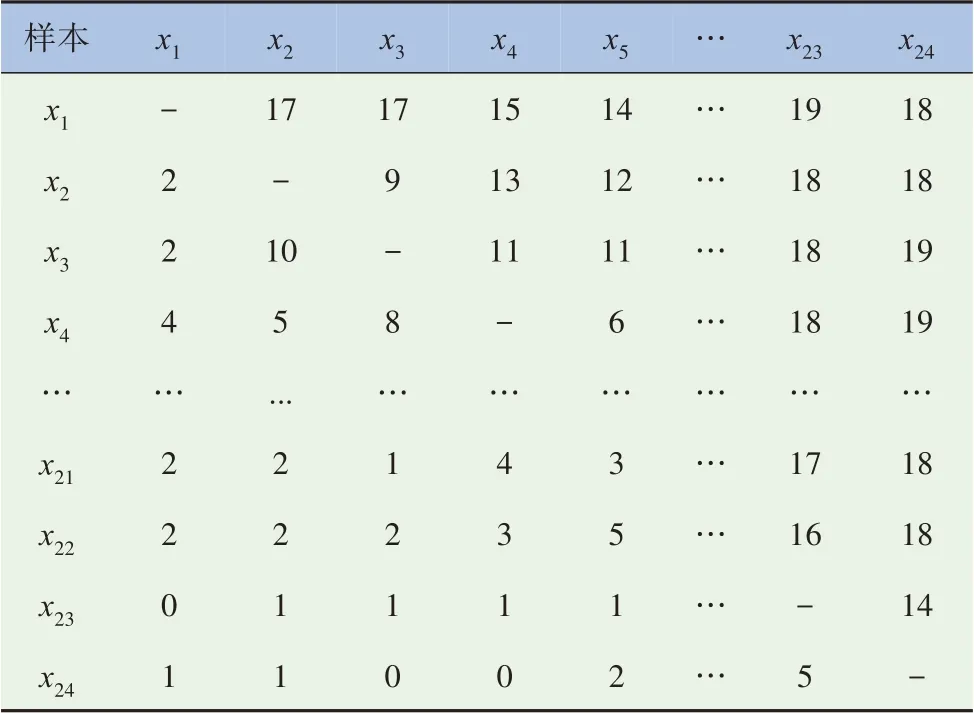
表3 平均总体

根据平均总体表，样本数为24，评审员19 人，所以每个样本评价比较总次数N=23×19，表3 中的数据是样本x声品质评价结果优于（不小于）x的得分n。由于每个评审员的评价结果相互独立，比较结果符合二项分布，所以可以通过Bradley-Terry 模型建立似然函数，根据式（5）对每个噪声样本声品质进行计算，将先验概率事件主观得分均值转换成后验概率事件声品质舒适度感知能力参数值。为方便数据处理和计算，以样本24（6 400/130（r·min）/Nm）为参考样本（保证模型收敛，设定其声品质感觉舒适度能力参数值为0），得到所用样本声品质舒适度感知能力参数值，并用其作为声品质主观评价得分。为便于表示，将噪声样本进行编号，如1 000/35（r·min）/Nm表示为1-35，见表4。

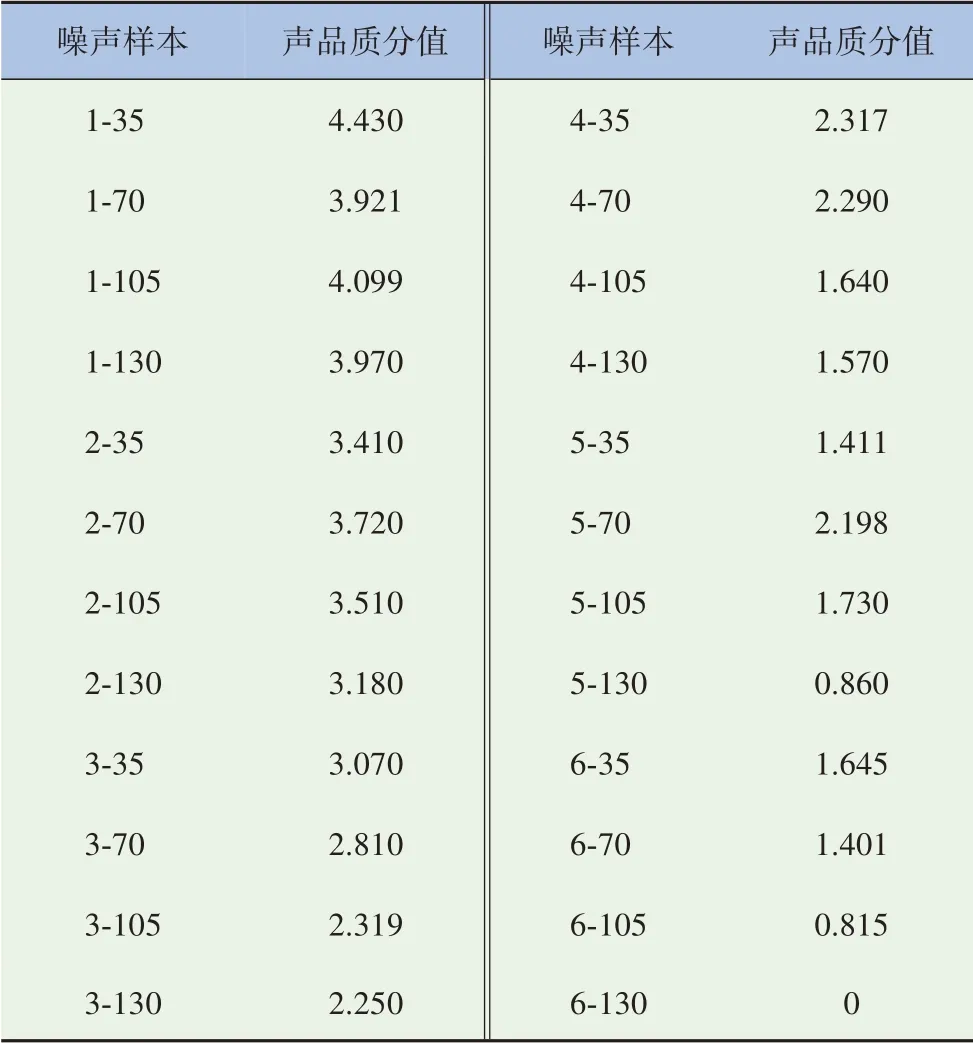
表4 声品质主观评价结果

3.2 声品质客观分析

为了更为系统全面地描述人对电机噪声的主观感知，将心理声学和物理学参量相结合对电机噪声进行分析评价。本文采用的客观评价参量有声压级L、响度（ISO532B）、尖锐度、粗糙度、波动度、音调度和语音清晰度A，通过LMS Test.Lab 的Acoustic Sound Diagnosis 模块进行计算，结果见表5。

表5 电机噪声信号客观参数

4 声品质预测模型搭建

探究声品质主观得分均值和声品质舒适度感知能力参数值对于声品质预测模型的精度差异，采用多元线性回归搭建永磁同步电机声品质预测模型，并对模型预测效果进行对比。为了避免客观参数处于不同数量级带来的影响，对客观参数按式（7）进行按行归一化处理，使数据之间具有可比性。

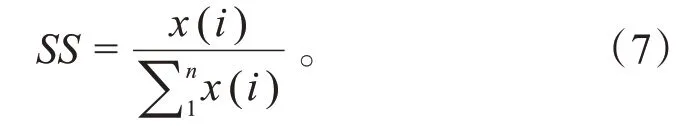
式中：为归一化结果；（）为待归一化数组。

4.1 多元线性回归模型

使用声品质能力参数值与客观评价参数值进行Pearson相关性分析，结果见表6。

由表6 可知，声压级、响度、尖锐度、语音清晰度与主观评价结果具备较明显的线性关系，可以作为因变量参与到多元线性回归预测模型的搭建。

表6 声品质能力参数值与客观参数值之间的Pearson系数

从噪声样本中随机取5 组噪声样本作为模型检验样本：2 000/70（r·min）/Nm，2 000/130（r·min）/Nm，3 000/35（r·min）/Nm，5 000/70（r·min）/Nm，

5 000/105（r·min）/Nm，剩余样本作为模型的训练样本，将声压级、响度、尖锐度、AI 指数、音调度作为模型的自变量，见表7。

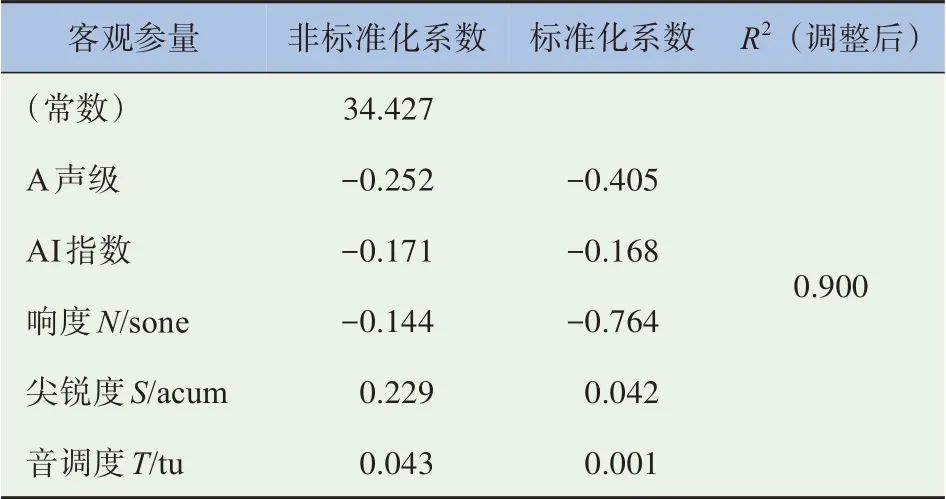
表7 多元线性回归系数

从表6～7 求解结果中得出声品质线性回归预测模型，如式（8）所示。

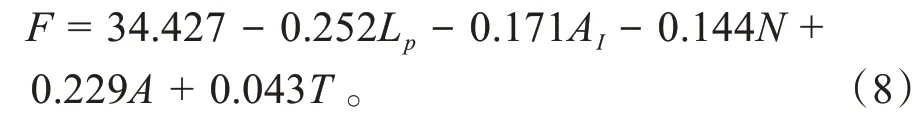
式中：L为声压级；为响度；为尖锐度；A为语音清晰度；为音调度。

将检验样本带入回归预测模型中，进行模型预测精度检验，结果如表8和图3所示。

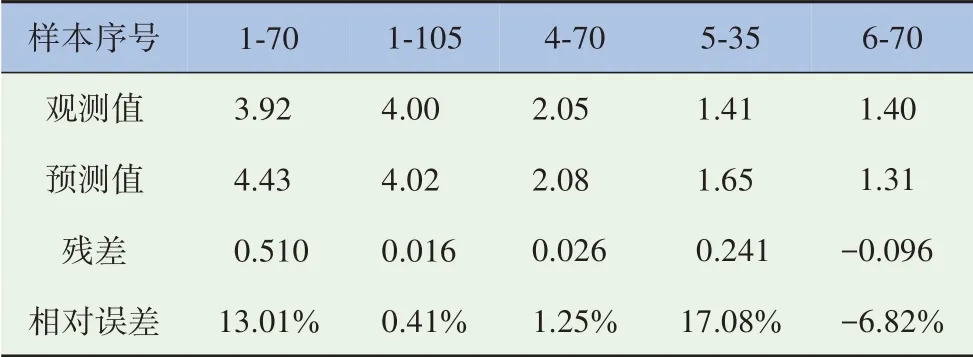
表8 多元线性回归模型预测结果

由表8、图3和图4可知，多元线性回归模型预测平均误差为9.64%，部分样本预测误差达到17.06%，预测误差较大，且预测结果不稳定，说明多元线性回归模型在永磁同步电机声品质预测中无法达到理想的预测效果，原因在于声品质与客观参数之间仅仅靠线性关系进行分析建模还不太全面，还需要考虑非线性关系。

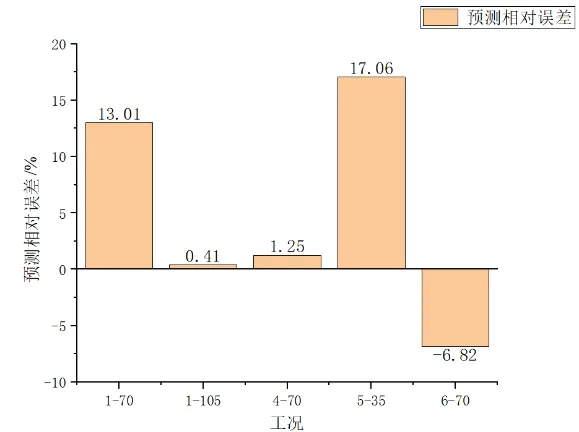
图3 多元线性回归模型预测相对误差

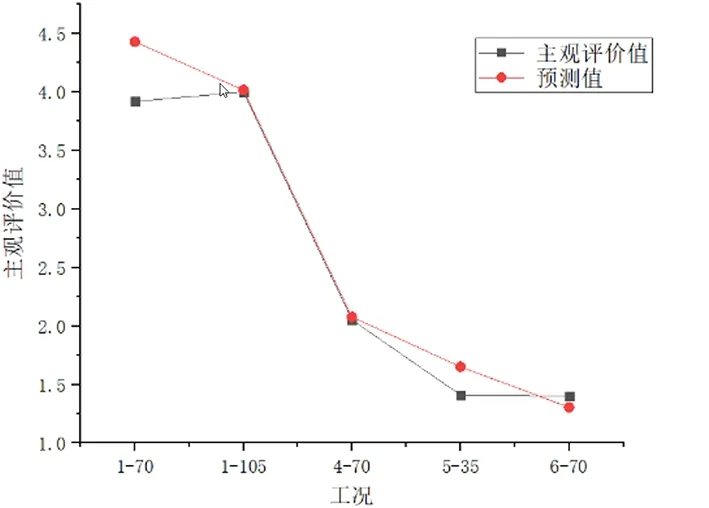
图4 多元线性回归模型预测结果

4.2 MPGA-RBF模型

RBF 神经网络是3 层前向型神经网络模型，其结构简单，学习效率高，且相比于BP 神经网络可直接由线性方程求解网络权值，避免了出现局部极值问题，其全局最有搜索能力，能实现最佳函数逼近。

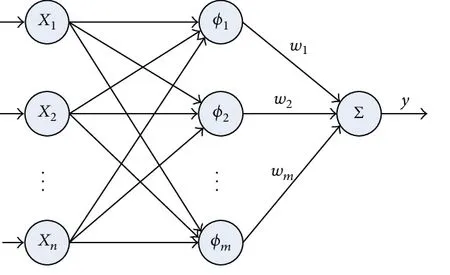
图5 RBF神经网络结构

由于采用梯度下降法优化网络参数，对于参数初始位置的设置具有较大的要求。倘若设置不当，会大幅度影响网络性能。因此，为了保证网络的性能必须对网络初始值进行寻优。

MPGA不仅可以优化RBF神经网络基函数中心点以及基函数宽度等网络初始参数，而且由于MPGA 是多种群不同参数（选择、交叉、变异）共同进化，通过移民算子实现种群间交流，通过人工选择算子实现精英个体的筛选，使MPGA避免了经典遗传算法SGA 出现的易早熟问题。MPGA-RBF网络结构如图6所示。

图6 MPGA-RBF神经网络结构

MPGA-RBF 初始参数设置中，种群数目设为10，种群内部个体总数为50，各种群交叉率在区间［0.7，0.9］随机选取，变异率在区间［0.001，0.05］随机选取，将归一化处理的训练样本带入MPGA-RBF 网络模型中进行训练，使用检验样本对模型训练结果进行检验，模型运行结果如表9和图7所示。

表9 MPGA-RBF预测结果

图7 MPGA-RBF迭代收敛曲线

遗传算法通过200 次迭代得到最优函数收敛值为0.007，达到了预期收敛值，且由图8～9 可知，该网络模型收敛速度快，网络预测精度高，平均误差为4%，说明该模型预测精度有了明显的提升，可以十分精准地实现对永磁同步电机声品质的评价预测。

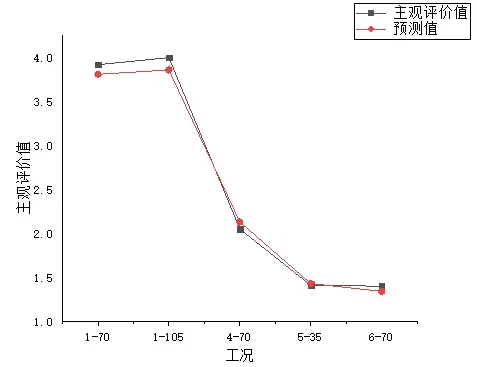
图8 MPGA-RBF模型预测误差

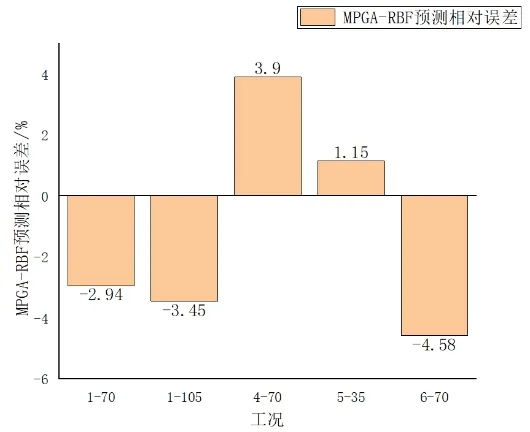
图9 MPGA-RBF模型预测结果

5 结论

本文针对永磁同步电机台架稳态噪声信号声品质开展了研究，对电机噪声特性进行了分析，确定了电机噪声成分，并基于Bradley-Terry 公式对成对比较法评价结果进行处理得到声品质能力参数值。以声压级、响度、尖锐度、音调度、语音清晰度、波动度、粗糙度为指标的客观参量为自变量，分别通过多元线性回归，用MPGA-RBF 神经网络搭建声品质预测模型。结论如下：

（1）声压级、响度、尖锐度、音调度、语音清晰度、波动度和粗糙度等客观参量与声品质主观评价结果之间存在不可忽视的非线性关系，仅靠线性关系搭建声品质预测模型无法保证模型的预测精度。

（2）在评审团成员有限的情况下，采用贝叶斯Bradley-Terry 公式对主观评价结果进行最大似然估计，将有限样本观测的先验概率事件转变成后验概率事件，可以降低事件观测值与真值之间的误差，提升模型的预测效果。

（3）综合RBF 神经网络和GA 算法的优缺点提出了MPGA-RBF 神经网络模型。从预测结果中得出，MPGA-RBF神经网络预测精度达到了96%，并且具备优良的收敛能力，能有效地对永磁同步电机声品质进行预测评价。