考虑共享停车的用户出行选择研究

常玉林，陈为华，孙 超

（1.江苏大学汽车与交通工程学院，江苏，镇江212013；2.东南大学城市智能交通江苏省重点实验室，南京211189）

随着经济的发展，全国汽车保有量不断增长，停车难已经成为车主的普遍担忧，停车位的不足，导致道路行驶的汽车增加，从而造成道路的拥堵，引发了一系列交通安全问题。近年来，由于互联网的发展，手机等高科技产品不断普及，“互联网+共享停车”模式应运而生，共享停车的出现缓解了停车的压力。

当前，对于共享停车研究主要集中于共享停车需求预测和共享停车泊位的分配，缺少共享停车对用户出行选择影响的研究。关于传统停车与出行选择的研究，雷坤峰等分析停车行为，建立广义出行费用函数，并构造路径选择模型。严海等针对特殊活动下的停车问题，提出了出行者选择行为的模型。宗芳等基于贝叶斯网络对停车行为进行分析。在现有的普通停车用户均衡模型中，四兵锋等构造了停车场广义效用函数，假定路径选择行为满足Wardrop 平衡原则，提出了停车流量分配的用户平衡模型。常玉林等根据停车选择理论和出行路径选择理论，提出了一种基于停车排队论下的随机用户均衡模型。LEURENT等根据停车容量的供需关系，建立了一种停车路径选择的用户均衡模型。上述的文献中，分开讨论停车选择和路径选择的问题，没有同时考虑停车和路径选择，在国内外文献关于同时考虑停车和路径选择研究中。GUR 等提出将停车选择和路线选择结合，建立用户均衡模型。李志纯等同时考虑了出行者对旅行路径和停车设施的选择，并建立了旅行选择和停车行为模型。四兵锋等基于概率论描述ATIS 条件下的停车和路径选择的问题，并建立随机用户均衡模型。虽然上述的文献中都有研究停车和路径选择的问题，但是缺少从路网的角度研究停车方式和路径选择之间的关系，并且不同停车方式的选择会影响出行路径的选择，可能会导致部分路段上的车辆出现拥挤的现象，从而影响整个交通网络。

基于上述分析，为了揭示共享停车、普通停车与路径选择三者之间的关系，本文将出行者分为共享停车和普通停车两类用户，结合NL 模型建立停车和路径的联合选择模型，构建关于共享停车流量和普通停车流量的用户均衡模型，最后通过一个交通网络算例，分析停车与路径选择的关系。

1 模型构建

构建一个带有两种停车方式（共享停车与普通停车）的交通网络(，，)，其中为路段节点，为所有停车设施集合，(，) ∈，为所有共享停车设施集合，为所有普通停车设施集合，为交通路网路段集合，∈。为所有OD 对的集合，为停车方式集合，∈(sp，op)，其中sp 为共享停车类型，op 为普通停车类型，为所有路径集合，(，) ∈，为从起点到停车设施的所有共享停车用户路径集合，为从起点到停车设施的所有普通停车用户路径集合。

1.1 共享停车的停车阻抗函数

假设出行者在选择共享停车方式时，需要提前预约，预约成功后，随机选择一条感知费用最小的路径到达停车场，到达预定的停车场后步行至目的地，则选择共享停车从起点到目的地的出行者广义费用为：

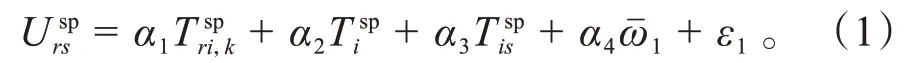
式中： 为共享停车用户从起点出发到达共享停车场的路径的行驶费用； 为出行者在共享停车场内搜寻停车位的费用； 为出行者从共享停车场到目的地的步行费用；ˉ为共享停车单位时间的预约费用；为共享停车用户的感知误差费用；～为待定系数。

1.2 普通停车的停车阻抗函数

选择普通停车的用户，如果选择的停车场没有空闲车位，则需搜索下一个停车场，直至找到空闲停车位，然后步行至目的地，这一过程增加了普通停车用户搜索停车场的费用，则普通停车用户的出行广义费用为：

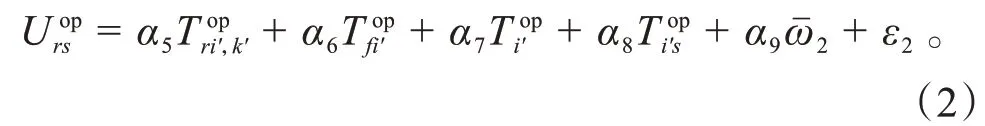
式中： 为普通停车用户从起点出发到达普通停车场的路径的行驶费用； 为搜索有空闲车位停车场的费用； 为出行者在普通停车场内搜寻空闲停车位的费用； 为出行者从普通停车场到目地的步行费用；ˉ为单位时间的停车费用；为普通停车用户的感知误差费用；～为待定系数。

1.3 基于NL模型的停车和路径联合选择

共享停车用户在出行前，需要提前预约停车位，明确停车场位置后，随机选择一条感知费用最小的路径到达停车场，而普通停车用户在出行前，根据先前经验，随机选择感知费用最小的普通停车场和出行路径。出行者选择停车方式和路径的选择都服从随机效用最大理论，满足两个出行选择步骤：（1）选择一个感知误差费用最小的停车方式；（2）选择一条感知误差费用最小的出行路径。构建一个NL联合选择模型结构，NL 模型的分层原则是将选择方案分解成若干层，选择方案类似性较大的分在同一层。如图1 所示，第1 层建立停车方式选择枝，有两种停车方式，分别为共享停车与普通停车，第2层建立路径选择枝。

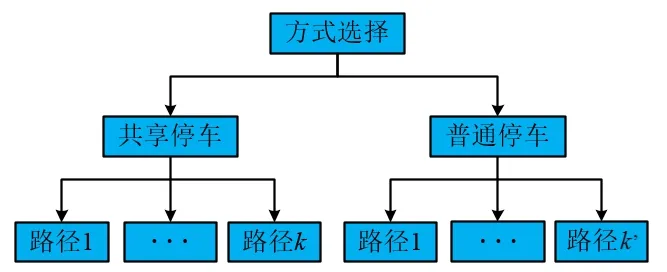
图1 NL联合选择模型结构

在第1层停车选择枝中，效用固定项为：

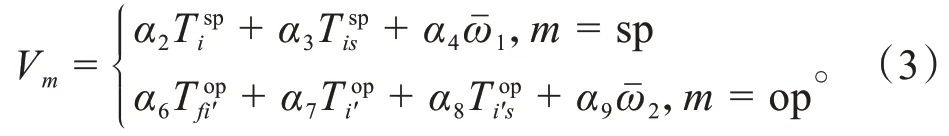
第2 层的出行路径选择枝中，在选择停车方式下，选择路径的效用固定项为：

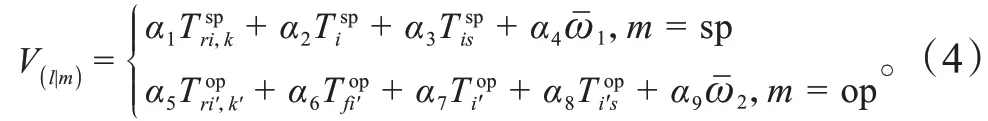
对于第1 层停车选择而言，选择共享停车sp 的概率为：

对于第2 层路径选择而言，在选择停车方式下，选择路径的概率为：

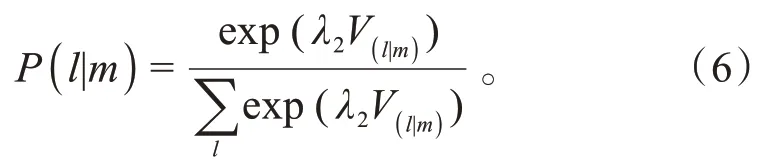
式（5）和式（6）中：表示第1 层随机效用项相关参数；表示第2层随机效用相关参数。

选择普通停车的概率为：

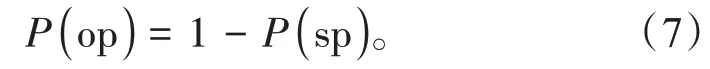
选择停车方式的同时又选择路径的联合概率为：

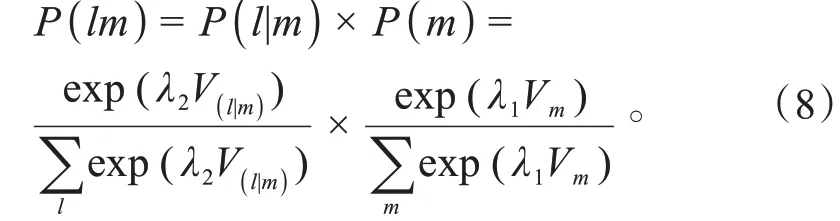
1.4 考虑共享停车的随机用户均衡模型

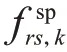
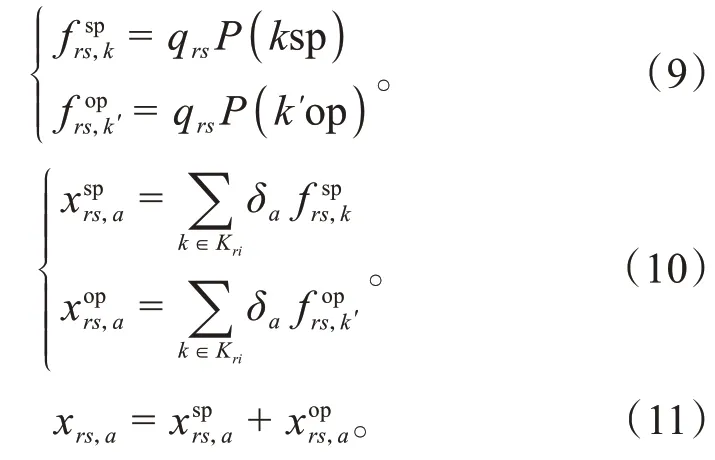
式（9）中，(sp)表示选择共享停车同时选择路径的联合概率；(kop)表示选择普通停车同时选择路径k的联合概率。式（10）中，若路段在路径上，则δ= 1，否则为δ= 0。

当交通网络达到均衡状态条件时，没有出行者能够通过改变停车方式和路径来减少出行的成本，满足下列式子：

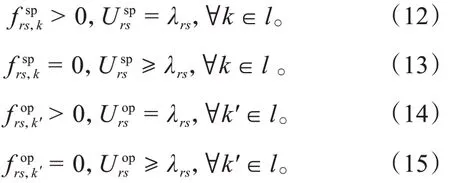
式（12）～（15）表示当某条路径上的停车流量大于0，则出行者的广义出行费用等于该OD 对的广义最小出行费用；若某条路径的停车流量等于0，则出行者的广义出行费用大于或者等于该OD对的广义最小出行费用，λ表示OD 对间用户出行的最小广义费用。

根据上述分析本文构造如下的随机用户均衡模型模型：

式（16）为带有共享停车流量和普通停车流量的用户均衡模型，式（17）为停车流量约束守恒约束，式（18）和式（19）为非负约束。

2 算法求解

针对以上提出的用户均衡模型，采用改进的相继平均算法（Method of Successive Average，MSA）进行求解，具体的求解步骤如下：

步骤1：初始化。设置初始迭代次数= 0，迭代终止误差= 0.000 1。根据零流量的初始阻抗和停车总需求q，执行一次Logit 加载得到初始选择路径的共享停车流量和初始选择路径的普通停车流量。

步骤2：成本值计算。根据式（1）和式（2）确定各个停车方式的出行成本值；根据NL 模型及式（5）和式（7）计算停车方式选择概率(sp)，(op)；确定共享停车和普通停车的分担量；运用式（8）计算不同停车方式下的路径联合选择概率()。

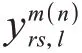
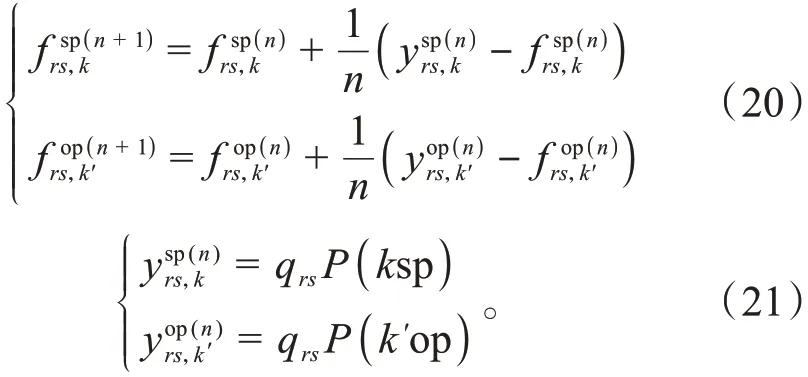
步骤4：收敛性验证。若收敛性满足收敛条件（22）或超过迭代最大次数，算法停止，并输出结果，否则令=+ 1，返回步骤2。

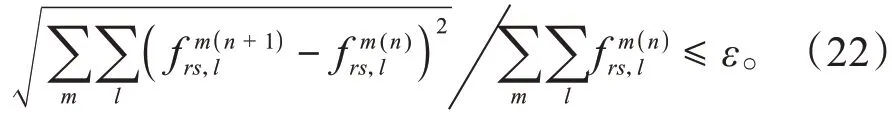
3 算例分析

如图2 所示，假设交通网络1 个OD 对之间，有5个路段节点，3个停车节点，分别为1个共享停车sp 节点和2 个普通停车（op1、op2）节点，有11条行驶路段、1 条搜索路段、3 条步行路段，假设OD对间停车流量的总需求为q= 600。

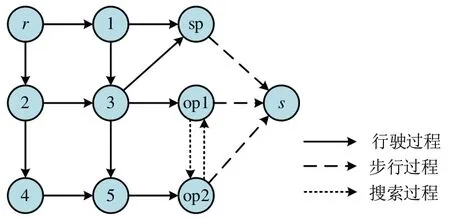
图2 交通网络

路段费用采用下列形式的BPR函数进行计算：

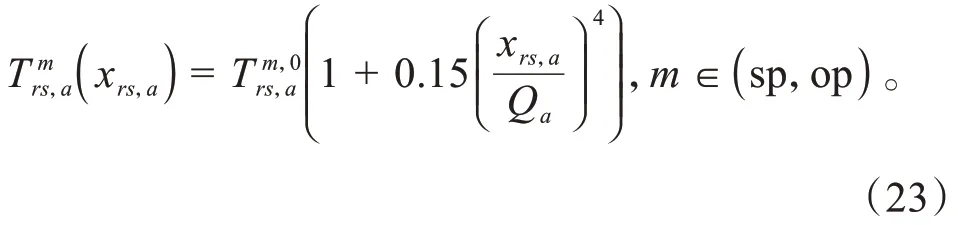
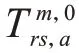
对于普通用户的停车场搜索费用同样采用BPR函数的形式进行计算：

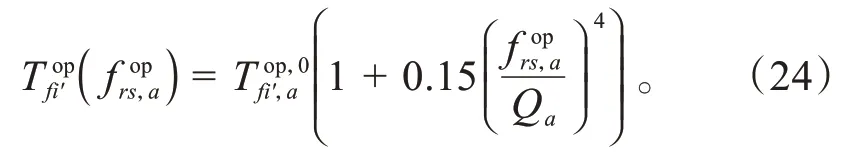
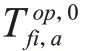
停车场内部车位的搜索费用采用文献［15］中所提出的公式计算：

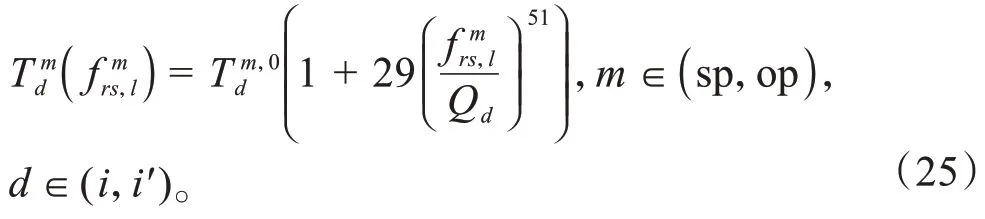
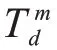
停车场的相关数据，包括停车收费、预约费用、步行费用T、停车场容量、停车场零流量的行驶时间见表1，路段的相关数据包括自由流行驶时间、路段容量Q见表2，表3 给出了各个参数的取值。

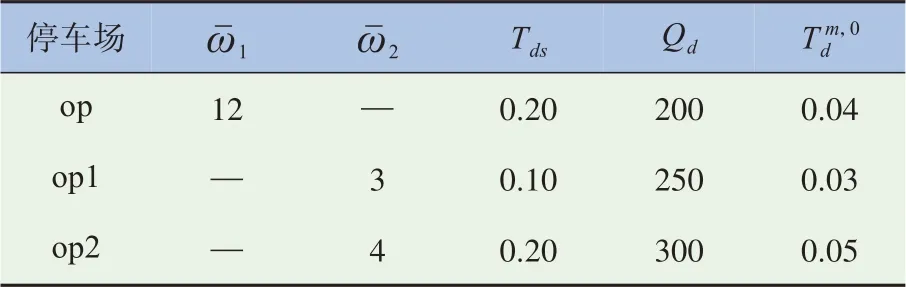
表1 停车场数据

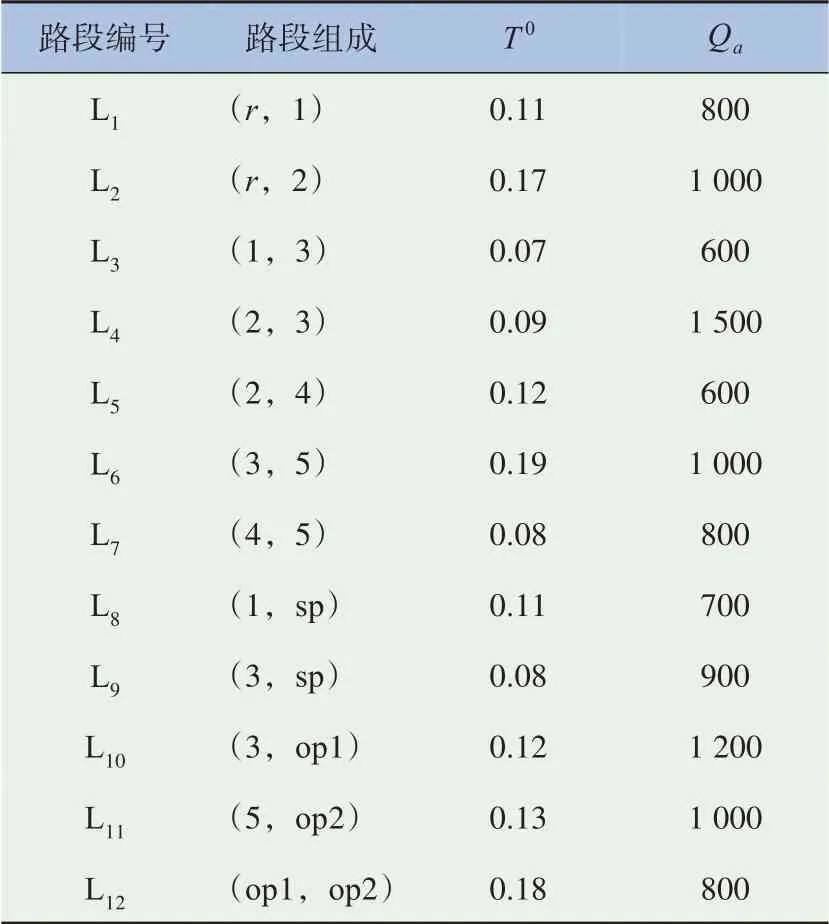
表2 路段数据

表3 相关参数取值

通过Matlab 对相继平均算法进行编程，得到不同停车方式下的路径流量及费用，由表4 可知，不同停车方式下的路径费用相差不大。这是因为选择共享停车和普通停车两类用户，路径的费用都是由路段费用和停车费用组成，相同停车方式的停车费用基本相等，所以路径上的费用主要体现为路段上费用的不同，而每条路段行驶的费用基本相等。因此，选择不同停车方式下的路径费用和路径流量计算结果相差不大。

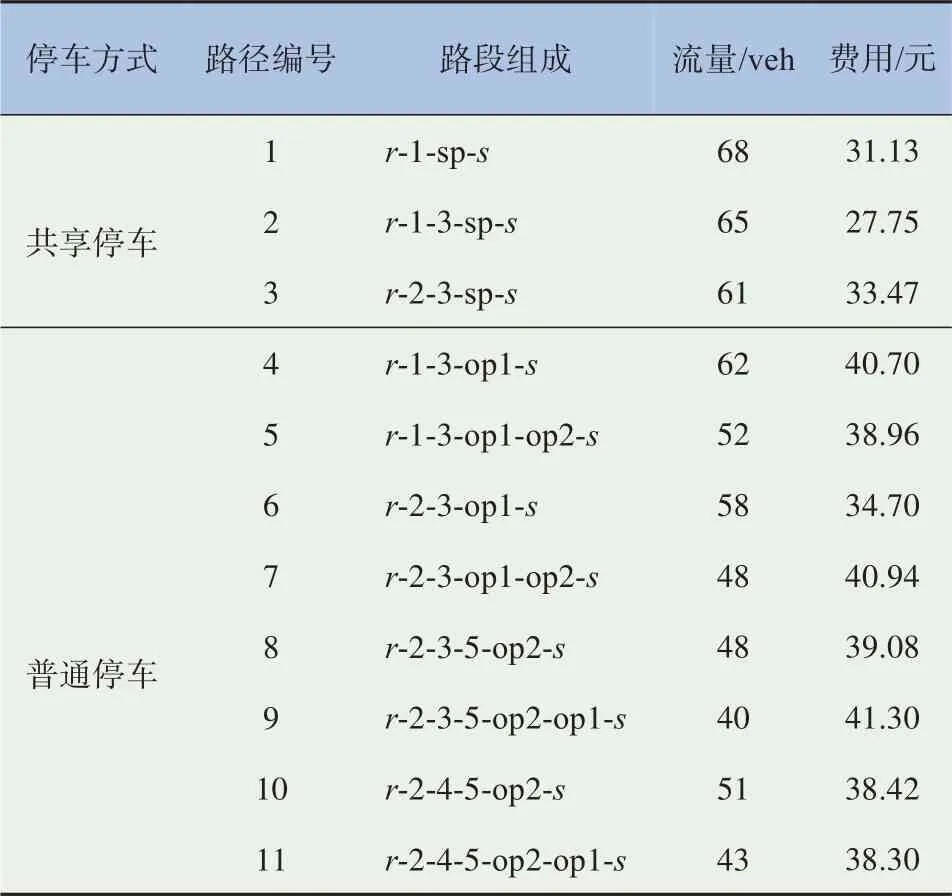
表4 路径流量及费用求解结果

图3表示不同预约费用下的停车需求变化情况，由图可知，随着预约费用的不断增加，选择共享停车方式的用户不断减少，而选择普通停车的用户则不断增加，说明预约费用对用户停车方式的选择影响较大。而图4中随着共享停车步行时间的增加，选择共享停车和普通停车的需求量基本保持不变，说明步行时间对用户停车方式的选择影响较小。

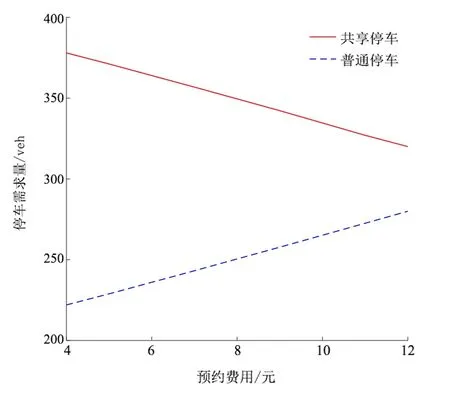
图3 不同预约费用下的停车需求量变化

图4 不同步行时间下的停车需求量变化

图5 展示了不同的共享停车预约费用与普通停车的停车收费（/）比例下路径联合选择的概率，图中明显可以看出随着比例的不断增加，路径1、路径2 和路径3 的路径联合选择概率都有下降趋势，而路径4、路径7 和路径9 都有明显上升的趋势，这是因为，随着比例的不断增加，选择共享停车方式的用户逐渐减少，因此，选择路径1、路径2 和路径3 前往共享停车场的路径流量也随之减少。相反地，随着比例的不断增加，选择普通停车方式的用户也不断增多，所以与普通停车场相连接的路径的流量也会不断增加，因此，路径选择呈明显的上升趋势。

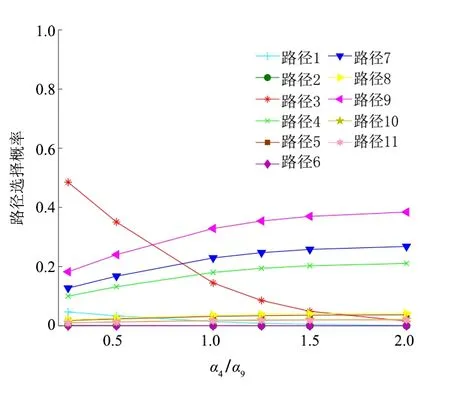
图5 不同的α4/α9比例下路径联合选择概率的变化

图6 进一步描述了考虑NL 模型和未考虑NL 模型的路径选择概率变化情况。在考虑NL 模型的情况下，几乎每条路径都有一定的选择概率，而在没有考虑NL 模型的情况下，路径2 占的路径选择概率最大，其他路径的选择概率几乎为0。这是因为在没有考虑NL 模型的情况下，由于只考虑路径的选择，没有同时考虑共享停车和普通停车两种方式的选择情况，并且在所有路径当中路径2 的路径费用最小，出行者往往更倾向于选择路径2，所以路径2 的选择概率会比较大。当考虑NL 模型时，在考虑了共享停车和普通停车的前提下，每个停车场都有一定的选择概率，再对路径进行选择，所以几乎每条路径都有一定的选择概率。

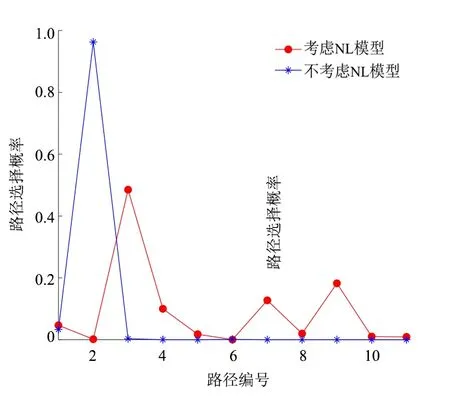
图6 不同模型下路径选择概率的变化

4 总结

本文考虑一个带有两种停车方式的交通网络，将出行者划分为共享停车和普通停车两类用户，然后分别对共享停车用户和普通用户建立停车阻抗函数。共享停车用户的停车阻抗函数由路段行驶费用、停车场内的车位搜索费用、预约费用、步行费用4 部分组成，普通停车用户的停车阻抗函数由路段行驶费用、停车场搜索费用、停车场内的车位搜索费用、停车收费、步行费用5 部分组成，通过上述的停车阻抗函数结合NL 模型，分析停车方式和路径之间的关系，建立停车方式和路径选择的联合概率，然后构建一个带有两类停车用户的随机用户均衡模型，并通过相继平均算法对模型进行求解，最后对算例进行分析。

通过算例分析发现预约费用从4 元变化到12 元时，共享停车需求量逐渐减少，普通停车需求量逐渐增多，而步行时间从0.05 h 变化到0.1 h时，共享停车需求量和普通停车需求量基本保持不变，不同的预约费用和停车收费之间的比例也在一定程度上影响出行者对路径的选择概率。分析还发现了考虑NL模型构建的用户均衡模型比不考虑NL模型更加符合实际的交通路网出行，能够为管理者对城市停车需求的管理提供可靠的理论依据。

本文不足之处在于，只将停车方式划分为共享停车和普通停车，而普通停车可以划分为好几类停车方式，例如路边停车、路外停车等，因此，未来的研究可将普通停车再进行划分，分析共享停车对这些停车方式和用户出行选择带来的影响。