哲学视角下的微积分课程思政元素挖掘

■ 周海阳，冯 郁

（南京审计大学统计与数据科学学院，江苏 南京 211815）

数学家波尔达斯说：“没有哲学，难以得知数学的深度；没有数学，也难以得知哲学的深度。”数学和哲学作为两门最古老的学科，从古到今，两者都是相互渗透，相互影响的。哲学指导和推进了数学的发展，为数学提供了研究方向；而数学同时也影响着哲学的观点，丰富和发展了哲学的内容。微积分是高等数学中研究函数的微分、积分以及有关概念和应用的数学分支[1]。恩格斯说：“微积分进入了数学，辩证法就进入了数学。”微积分的创立是人类数学史上的一次重要飞跃，其中很多概念和方法都蕴含着哲学思想，具有深刻的哲理。

一、微积分发展史中的哲学思想

微积分是财经类专业本科生的一门重要基础课，是培养经济类创新人才的重要课程。在高校双一流建设的背景下，加强微积分课程建设既能够为高校未来发展奠定坚实的基础，也是实现培养创新人才目标的重要支撑。同时，为了实现中华民族伟大复兴的中国梦，微积分教学还需要着眼于培养拥护中国共产党领导和社会主义制度、立志为中国特色社会主义事业奋斗终生的有用人才。

课程思政是指以构建全员、全程、全课程育人格局的形式将各类课程与思想政治理论课同向同行，形成协同效应，把立德树人作为教育的根本任务的一种综合教育理念[2]。那么如何顺应时代要求，在微积分教学中挖掘课程思政元素呢？教师可以从哲学的角度，挖掘微积分课程思政元素，让学生更好地理解所学知识，并具有一定的辩证思维能力，还可以结合中华优秀传统文化教育，结合社会主义核心价值观，培养学生健康的人格和正确的人生观、价值观、世界观[3]。

微积分从产生，发展，再到完善，经过了漫长的时间，其中也伴随着哲学思想的应用和体现。微积分最重要的思想就是“无限逼近”的极限思想，而极限思想早在中国古代就已经产生，如《庄子·天下篇》中所述“一尺之棰，日取其半，万世不竭”和刘徽在割圆术中提到的“割之弥细，所失弥少，割之又割以至于不可割，则与圆合体而无所失矣”都体现了极限思想的萌芽。

古希腊数学家阿基米德的“平衡法”，是“将需要求的未知量（面积、体积等）分成许多微小单元（如微小线段、薄片等），再用另一组微小单元（总和比较容易计算）来比较，但需要建立一个杠杆，使前后两组获得平衡”[4]，平衡法体现了近代积分法的基本思想。而在微分学中，罗尔定理、拉格朗日定理和柯西定理这三大微分中值定理，条件逐个削弱，体现了从特殊到一般的规律。

17世纪下半叶，牛顿和莱布尼茨在解决求面积、求切线的问题中先后创立了微积分基本公式，即牛顿-莱布尼茨公式。莱布尼茨与牛顿谁先发明微积分的争论是数学界至今最大的公案。莱布尼茨于1684年发表第一篇微分论文，定义了微分概念，采用了微分符号dx，dy。1686年他又发表了积分论文，讨论了微分与积分，使用了积分符号∫。依据莱布尼茨的笔记本，1675年11月11日他便已完成一套完整的微分学。然而1695年英国学者宣称，微积分的发明权属于牛顿；1699年又说，牛顿是微积分的“第一发明人”。1712年英国皇家学会成立了一个委员会调查此案，1713年初发布公告：“确认牛顿是微积分的第一发明人。”牛顿在1687年出版的《自然哲学的数学原理》的第一版和第二版写道：“十年前在我和最杰出的几何学家莱布尼茨的通信中，我表明我已经知道确定极大值和极小值的方法、作切线的方法以及类似的方法，但我在交换的信件中隐瞒了这方法……这位最卓越的科学家在回信中写道，他也发现了一种同样的方法。他并诉述了他的方法，它与我的方法几乎没有什么不同，除了他的措词和符号而外”。牛顿-莱布尼茨公式是联系微分学与积分学的桥梁，它证明了微分与积分互为逆运算，体现了两者对立统一的关系，同时也标志着微积分的正式形成。

微积分的发展过程中也充满了矛盾和争论，在建立了微积分基本公式后，人们发现微积分中的一些问题缺乏必要的逻辑基础，尤其是英国主教贝克莱针对求导过程中无穷小的质疑，引发了第二次数学危机[5]。这场危机的解决最终完善了微积分的理论系统，充分体现了微积分的发展是循环往复、螺旋向上的。恩格斯说：“变数的数学——其中最重要的部分是微积分——本质上不外是辩证法在数学方面的运用。”这正是对微积分发展史中哲学思想的高度概括。

二、微积分课程思政中的哲学定律

（一）对立统一规律

对立统一规律是唯物辩证法的实质和核心，世界上任何事物的内部和事物之间都包含矛盾的两个方面，矛盾的双方既对立又统一[6]。

微积分中通过局部来研究整体，通过整体来推测局部，是一种经常使用的方法。如一元函数的最值是整体概念，是比较整个定义内所有点的函数值，其中函数值最大的称为最大值，函数值最小的称为最小值。而极值则是局部概念，指在点x0的某一邻域内，即在局部小范围内，比较函数值的大小[5]。而若f(x)在[a,b]上连续，那么f(x)在[a,b]上必有最大值和最小值，求最值的方法就是先求出f(x)在[a,b]内的所有极值，再求出f(a)和f(b)，最后比较这些值的大小。函数的极值和最值便是具有局部和整体的对立统一关系，可以通过极值（局部）来求出最值（整体）。

这样的对立统一关系与我们的生活密切相关，从个人发展历程来看，我们的人生正是通过一个个阶段的努力奋斗，实现一个个小目标（极值），最终达到人生的巅峰（最值）。从党的发展历程来看，我们党对社会主义现代化建设的战略谋划，正是把宏伟目标分解成一个个切实可行的具体目标和任务，有步骤、分阶段完成，不断推进中国特色社会主义事业取得新的胜利。从1964年，周恩来同志在三届全国人大一次会议上正式提出“四个现代化”的奋斗目标，到改革开放后，邓小平同志明确提出现代化建设“三步走”设想，再到党的十八大上提出到2020年实现全面建成小康社会奋斗目标，一直到党的十九届五中全会上对“十四五”时期我国发展作出系统谋划和战略部署，中国特色社会主义进入新时代。

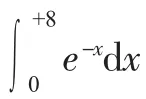
在这样一个似乎违反常规的例子中，我们看到了有界和无界的对立统一性，而在平时的学习生活中也会遇到许多类似于无界区域面积的问题，它们看似不可能完成，但实际上却是可以完成。

例如，2012年，中国共产党的十八大提出到2020年实现全面建成小康社会宏伟目标并消除绝对贫困是最重要指标。而当时的情况是，中国还有近一亿农村贫困人口。在外界一些人看来，要想让近1亿人在几年内摆脱贫困，对中国而言几乎是一个“不可能完成的任务”。就在中国脱贫攻坚战进入收官阶段，2020年，新冠肺炎疫情突如其来，在疫情防控和稳经济促发展的双重压力下，中国要想如期全面完成脱贫任务，难上加难。然而，中国人在磨难中奋起，面对全球疫情，率先控制疫情，经济由负转正，如期完成脱贫任务，完成了“不可能完成的任务”。

（二）量变质变规律

任何事物的变化都是由量变到质变的过程，量变到一定程度引起质变。量变是质变的基础和准备，质变是量变的必然结果[5]。

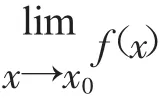
量变质变规律不仅存在于微积分的运算性质中，也存在于我们国家的经济发展历程中。新中国成立之初，在很长一段时间里我国都处于物质匮乏阶段，经济发展远远不能满足人民群众对物质生活的需求。国家通过大力发展传统产业，生产更多数量的产品来满足人民群众的生活需求。到20世纪90年代，传统产业的生产能力跟不上市场需求，出现严重的产能过剩，生态环境问题日益严重，经济高质量发展的重要性愈发显现。从大炼钢铁到蛟龙入海、北斗卫星导航、神州十三号圆梦天宫，从医药进口到独立研发出青蒿素、研制出新冠肺炎疫苗，从制造大国到科技大国，中国经济正在经历从量变到质变的过程。

微积分教学中引入课程思政实际上也是一次又一次量变引起质变的过程。其中，量变是开展一次次微积分教学活动，质变是对思想政治理论的领悟。要让学生产生质变，仅靠一次量变是无法实现的。领悟任何一个理论都需要一个积累的过程，所以微积分教学中融入课程思政也是一个长期的过程，需要学生不断巩固和深化所学知识，主动思考思想政治理论的正确性和先进性，从而自觉树立正确的世界观、人生观、价值观。

（三）否定之否定规律

新事物否定旧事物，然后被更新的事物否定，一切事物都是如此“螺旋式”向前发展，否定之否定规律揭示了事物发展的趋势和道路[5]。

在引入定积分概念时，我们计算了曲边梯形面积。把曲边梯形分成若干个小曲边梯形，用小矩形面积近似代替小曲边梯形面积，再把所有小矩形面积相加，得到曲边梯形面积的近似值[7]。最后令划分充分得细，即每一个小矩形的底都趋于0，则小矩形面积和的极限即为曲边梯形的精确面积。这种“以直代曲”又“由曲到直”的思想正是否定之否定规律的体现。

正如恩格斯所说，“在更高的阶段上重新达到原来的出发点”。这即为否定之否定规律所揭示的客观规律，回到起点，又高于起点[8]。从人类社会发展来看，所有制的演变也是这样一个循环往复、螺旋上升的过程。从氏族公社的原始公有制社会到封建主义和资本主义的私有制社会，再到共产主义高级发达的公有制社会，我们的共产主义理想是建立在科学基础上的，我们要坚持共产主义不动摇。

对于在微积分教学中引入课程思政这种新的教学理念，大部分教师都是摸着石头过河，也是从无意识到有意识再到无意识，也经历了否定之否定的过程。由于每一个人都有自己固定的思维模式，这种思维模式往往会让教师的思维产生局限性，所以教师还需要在不断摸索中打破思维定式，参与集体讨论，邀请思政课教师参与到课程讨论中来，协同合作，共同提高课程思政的效果。

三、微积分课程思政的途径

微积分这门课程的特点是内容抽象、推理严谨及应用广泛，许多内容都与哲学思想存在着密切联系。在微积分教学中，应该抓住课程思政这个重要形式，在挖掘哲学思想的基础上，找准切入点，遵守教育规律，达到全面培养人的目的。

（一）课堂教学中融入微积分发展历程

微积分是17世纪以来，经过许多数学家的努力建立起来的，它是人类最伟大的成就之一，牛顿、柯西、莱布尼茨、拉格朗日等数学家追求真理的精神值得我们学习。在建立微分、导数、中值定理、微积分基本公式等重要概念和定理时都经历了反复探索、不断尝试的过程。教师可以在课堂教学中介绍微积分发展史中的小故事，使理性严谨的数学课堂兼具人文色彩，让一些有“数学恐惧症”的学生更好地理解所学知识，无形中减轻他们对数学的恐惧[9]。

（二）理论联系实际，合理开展课程思政

哲学思想融入微积分教学中，要将微积分基本公式中的对立统一规律、二元函数的量变质变规律和求曲边梯形面积的否定之否定规律自然地加入授课环节，把一些在数学范围内难以理解的问题通过哲学的角度来解释，起到四两拨千斤的效果。利用哲学思想，并结合社会实际，进行潜移默化的思想政治教育[10]。

（三）主动学习哲学原理，提高课程思政效果

教师要将哲学原理渗透融合到微积分教学中，不仅自身要学习哲学和自然辩证法知识，运用哲学原理分析微积分知识体系，也要提倡学生学一点哲学，学一点辩证法，提高他们理解问题、解决问题的能力。从被动地学习微积分知识，转化为运用微积分思想解决实际问题，这是微积分教学的更高目标，也是课程思政的更高目标。

在微积分教学中，应该抓住课程思政这个重要形式，在挖掘哲学思想的基础上，找准切入点，遵守教育规律，以人才培养为核心，不忘初心，牢记使命，帮助学生在人生道路上形成良好的人格，树立正确的人生观、价值观、世界观。