融合输入整形和滑模的锻造机器人振动抑制

袁明新，王丽丽，陈卫彬，邱贝贝，徐玉松

(1.江苏科技大学 冶金与材料工程学院，江苏 张家港 215600；2.中国船舶重工集团公司 第七一六研究所产业部，江苏 连云港 222002；3.连云港杰瑞自动化有限公司 事业部，江苏 连云港 222006)

0 引言

锻造车间内充斥着振动、噪音、粉尘和高温等，这不仅给安全生产带来隐患，还降低了生产效率。随着智能制造技术的发展，锻造机器人生产线受到了重点关注。然而，锻压机工作时的冲击振动一直是影响锻造机器人控制精度的重要因素[1-4]。虽然生产线上的锻压机设备通常会通过底部增加隔振[5-6]来吸收振动，但仍然不可避免地有少量冲击会通过地基传递给锻造机器人，并形成残余振动来影响机器人夹持精度。如何有效抑制振动不仅是锻造机器人需要解决的难题，还是控制领域的研究难点。目前，国内外专家针对主动振动抑制研究主要从开环控制、闭环控制和开闭环混合控制3个方面开展。

在开环控制中，DAN等[7]为抑制机械臂在点对点运动过程中产生的振动，提出了分数延迟时变输入成形技术，并开发了可识别和映射机械臂主振型固有频率和阻尼比的新工具。实验结果表明，该技术可降低机械手的残余振动，但仅考虑了机械手自身的柔性振动，忽略了外界环境的振动影响；KOBILOV等[8]为消除工业机器人定位系统中由重复运动引起的振动，通过虚拟频率参数来调整延迟时间进而消除残余振动，但当振型频宽相差很大时，抑制效果会变差。

在闭环控制中，金国光等[9]利用滑模变结构对刚—柔性机械臂末端的弹性变形进行振动抑制研究，仿真结果显示，刚—柔性机械臂的抖振被减少，达到了预期控制效果，但未对滑模控制器参数选择作进一步研究和分析；黄宣睿等[10]为解决柔性关节工业机器人的末端抖振，在传统PI控制基础上提出了关节伺服系统的振动抑制算法，该方法能有效抑制机械振动，但对由自身柔性所导致振动的抑制效果不佳；ALANDOLI等[11]针对柔性连杆机械手的末端振动问题，采用基于模糊控制与最优线性二次型调节器相结合的智能最优控制器，实现了机械臂末端振动的有效抑制，但该设计复杂，在实际工程的应用中较困难。

在开闭环混合控制中，贾鹏霄等[12]为解决柔性关节机械臂的振动，提出了基于比例—微分(Proportional-Derivative, PD)自适应控制与输入整形技术相结合的复合控制方案。仿真结果表明，该方案可以实现很好的振动抑制效果，但系统响应速度慢、性能不稳定；HAKAN等[13]针对起重机系统由自身质量导致的残余振动，设计了混合控制方案，将零振动输入整形方法应用于开环控制，将BP、广义回归和径向基函数网络串联作为闭环智能控制方法，但该方案只适用于有效抑制由自身质量造成的残余振动，无法解决外界冲击造成的系统残余振动；SHE等[14]为抑制伺服系统的振动，将输入整形技术和自适应模型跟踪控制相结合，仿真结果表明，该方法在振动抑制方面具有一定的优越性，但在实施过程中需要精确预估振动行为，鲁棒性有待提高。

相比开环控制和闭环控制，开闭环混合控制综合了两者优点，已成为当前主动振动抑制研究的主攻方向。但现有主动振动抑制策略更多关注被控对象自身的振动，忽略了外界环境对被控对象的干扰。而锻造机器人生产线的残余振动正来自外界锻压机冲击，是影响机器人控制精度的重要因素。鉴于此，本文开展了融合输入整形和滑模控制的残余振动抑制策略研究。首先设计了残余振动抑制方案；然后围绕方案中的输入整形器、滑模控制器进行了设计和分析；最后利用MATLAB/Simulink平台进行了残余振动抑制效果的数值测试。

1 锻造机器人残余振动抑制方案设计

众所周知，锻造机器人生产线中的锻压机等设备在工作时会产生强烈的脉冲冲击，并通过地基传递给锻造机器人形成残余振动，这不仅降低了锻造机器人末端执行器的控制精度，还降低了工作效率。为此，结合冲击振动源特征以及控制要求，本文设计了如图1所示的残余振动抑制方案。

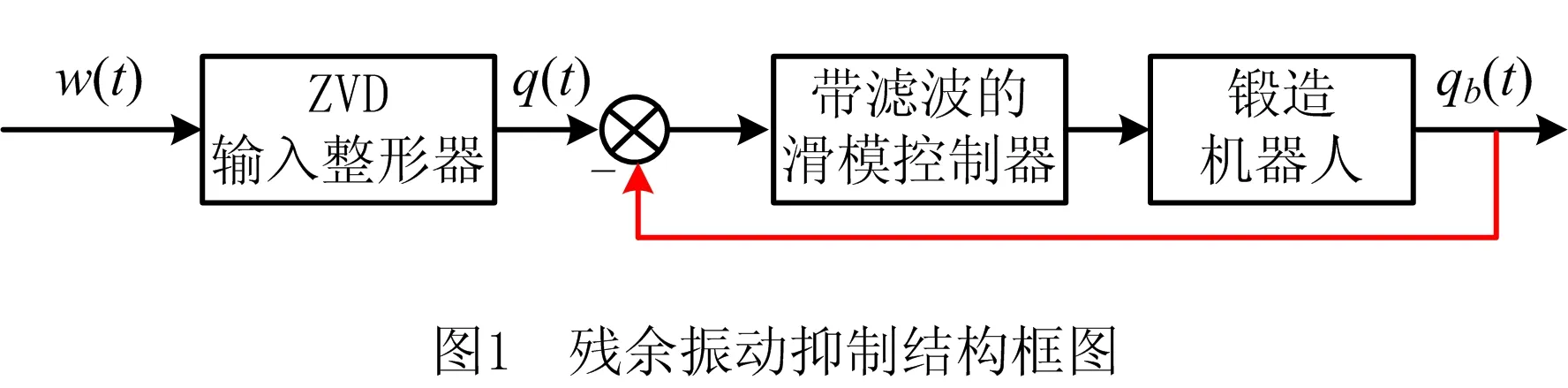
该方案采用开闭环混合控制策略，其中开环控制拟采用零振动微分(Zero Vibration Differential, ZVD)输入整形器，对锻压机冲击信号w(t)进行整形，从而对干扰信号进行前期抑制；随后根据六自由度锻造机器人动力学模型设计滑模控制器，将整形后脉冲信号q(t)输入滑模控制器，并引入滤波器来消除滑模变结构中抖振；最后将经过输入整形和滑模控制器的信号传递给锻造机器人，并根据系统的当前状态进行调整，使得信号qb(t)能够按照预期轨迹运动。

2 输入整形器设计及分析

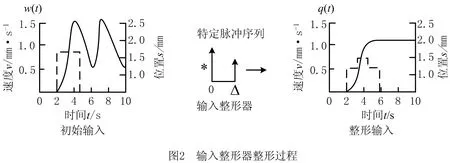
输入整形器的设计和添加旨在对锻造机器人残余振动先行抑制，如图2所示为输入整形器的整形过程。初始输入信号w(t)在某时刻与特定脉冲序列进行卷积后产生系统输入信号q(t)，实现对初始信号幅值的有效抑制。

2.1 输入整形器的设计方法

锻造机器人本体通常采用六自由度机械手。为了便于设计输入整形器的开环控制和分析响应效果，将机械手降阶为：

(1)

式中：ωn为锻造机器人柔性臂固有频率，ξ为柔性臂阻尼比。

含有多个特定脉冲序列的输入整形器可描述为：

(2)

式中：i=1,2,…,n，n为脉冲数;Ai为脉冲i幅值;ti为对应时滞。

锻造机器人系统的单位脉冲响应为：

(3)

引入输入整形器后系统的响应为：

(4)

(5)

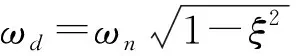
系统残留振荡百分比为：

(6)

式中：

(7)

(8)

2.2 输入整形器选取

由式(2)不难看出，如何选取脉冲数n、各脉冲幅值Ai和时滞ti是整形器的设计关键。基于锻造机器人系统要求，Ai的大小决定了输入整形器对残余振动抑制的能力大小。脉冲数n越大，整形器鲁棒性越高，但也会增大时滞，进而降低系统响应速度。为了使整形器的鲁棒性和时滞达到最佳平衡，本文选用三脉冲零振动微分(ZVD)输入整形器，令V(ω,ξ)=0。此外，还需增加鲁棒性约束方程，令V(ω,ξ)对ω的导数为0，其约束方程如下：

(9)

(10)

简化式(10)可得：

(11)

(12)

脉冲幅值和时滞约束方程为：

(13)

联立式(9)、式(11)～式(13)可求得ZVD输入整形器的脉冲幅值Ai为：

(14)

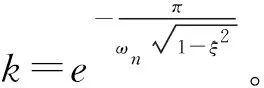
脉冲时滞ti为：

t1=0,

t2=T/2,

t3=T。

(15)

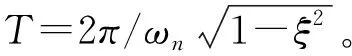
计算出ZVD输入整形器的参数如下：

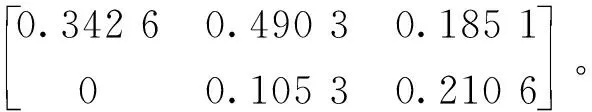
3 锻造机器人动力学建模

为了实现锻造机器人振动抑制的闭环滑模控制，建立其动力学模型是首要条件[15]，为此本文利用拉格朗日法，以能量方式构建锻造机器人机械臂动力学模型，不仅能避免对复杂约束条件计算，还能节省建模时间。图3给出了锻造机器人柔性机械臂的物理建模。

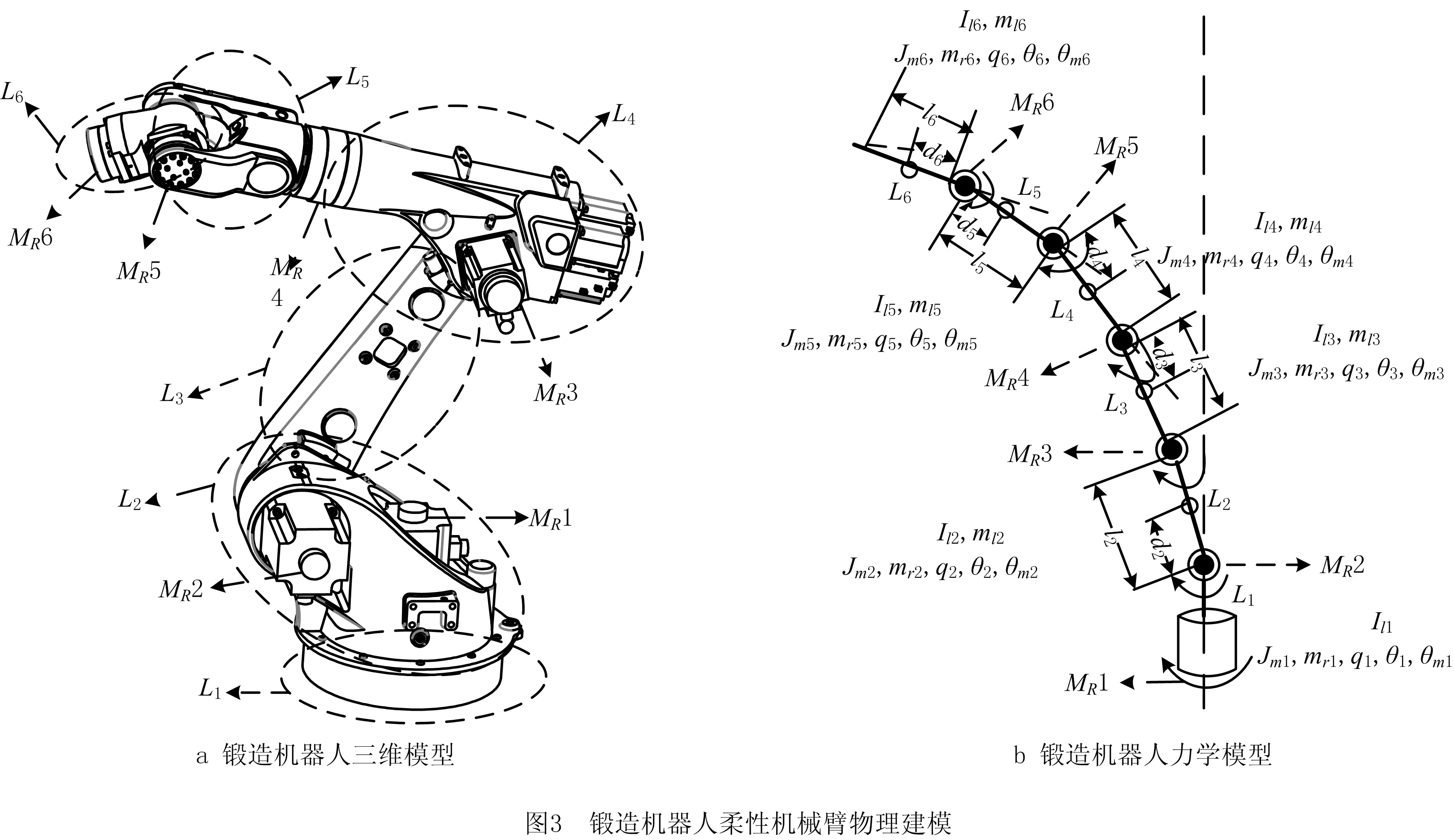
图中：Jmi为电机i(i=1,2,…,6)转子的转动惯量；Ili为连杆i的转动惯量；mli为连杆i的质量；mri为电机i转子的质量；θmi为电机i经过减速前的角度；qi为关节i的连杆端角位移；di、li分别为连杆i的质心距离和连杆长。

3.1 锻造机器人机械臂动能分析

对六自由度锻造机器人机械臂的电机转子和连杆进行动能分析可得：

(1)电机MR1转子动能为：

(16)

(2)连杆L1的动能为：

(17)

(3)电机MR2转子动能为：

(18)

(4)连杆L2的动能为：

(19)

式中s2=sinq2。

(5)电机MR3转子动能为：

(20)

(6)连杆L3的动能为：

(21)

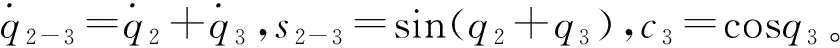
(7)电机MR4转子动能为：

(22)

(8)连杆L4的动能为：

(23)

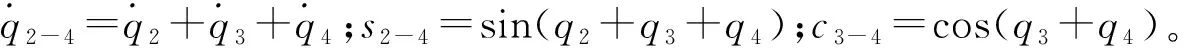
(9)电机MR5转子动能为：

(24)

式中c4=cosq4。

(10)连杆L5的动能为：

(25)

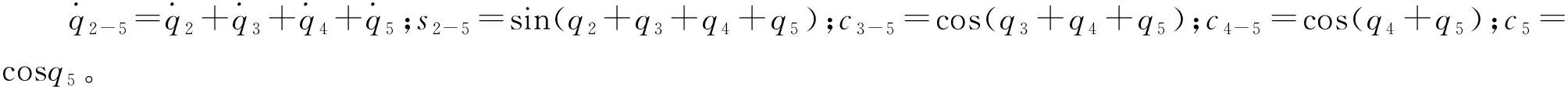
(11)电机MR6转子动能为：

(26)

(12)连杆L6的动能为：

Tl6={ml6[(l2s2+l3s2-3+l4s2-4+l5s2-5+d6s2-6)2

(27)

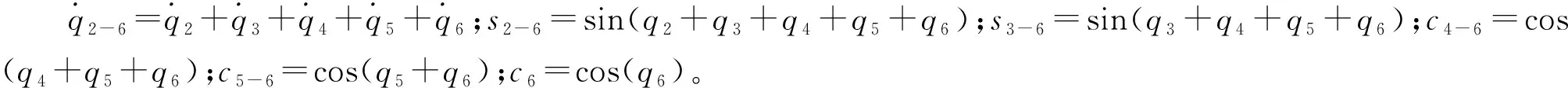
综合式(16)～式(27)可得锻造机器人柔性关节系统总动能T为：

(28)

3.2 锻造机器人机械臂总势能

由于锻造机器人机械臂的关节具有柔性，本文建模时根据Spong模型将其定义为线性弹簧，该关节的弹性势能为：

(29)

式中：Ki为关节i刚度；θi、qi分别为关节i电机端和连杆段的角位移。

则六自由度锻造机器人机械臂总的弹性势能为：

(30)

六自由度锻造机器人机械臂的总重力势能为：

PG=g[ml2d2c2+mr3l2c2+ml3(l2c2+d3c2-3)+

mr4(l2c2+l3c2-3)+ml4(l2c2+l3c2-3+d4c2-4)+

mr5(l2c2+l3c2-3+l4c2-4)+ml5(l2c2+l3c2-3+

l4c2-4+d5c2-5)+mr6(l2c2+l3c2-3+l4c2-4+

l5c2-5)+l3c2-3+l4c2-4+l5c2-5)+ml6(l2c2+

l3c2-3+l4c2-4+l5c2-5+d6c2-6)]。

(31)

则六自由度锻造机器人机械臂的总势能为：

P=PZ+PG。

(32)

3.3 锻造机器人机械臂动力学方程

将式(28)和式(32)代入Lagrange方程：

L=T-P,

(33)

可以得到六自由度锻造机器人系统的动力学方程为：

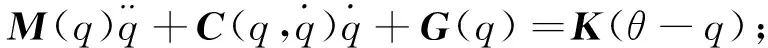
(34)

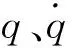
4 滑模控制器设计及分析

锻造机器人机械臂是一个非线性的高阶系统。在工作过程中，由于参数和外部干扰等不确定因素的存在，使得锻造机器人系统很难在线辨识和控制。为此，本文在闭环控制中使用能够快速实现结构响应且具有很强鲁棒性的滑模变结构。

4.1 带滤波器的滑模控制器设计

滑模控制器不可避免会出现抖振，本文通过增加低通滤波器[16]来解决该问题。

锻造机器人动力学模型如式(34)所示，所增加低通滤波器设置如下：

(35)

式中ηi为状态i的滤波控制因子，且ηi>0。低通滤波器设置为：Q(s)=25/(s+25)。

控制系统与滑模控制器的关系可表示为：

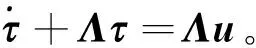
(36)

式中：Λ=diag(λ1,λ2,…,λn)，λi>0，i=1,2,…,n，n为输入的控制信号数;u为滑模控制率。

设理想位置指令为qb(t)，跟踪误差表示为：

e(t)=q(t)-qb(t)。

(37)

设计滑模面[17]为：

(38)

式中Λi=diag(λi1,λi2,…,λin)，λij>0，i=1,2，j=1,2,…,n。

将式(36)带入式(34)中可得：

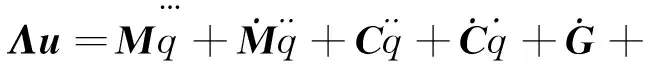
(39)

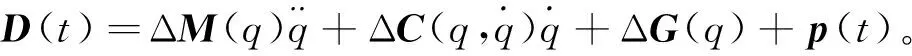
(40)

式中D(t)为系统的不确定状态，代表了各种干扰以及测量精度等不确定因素的综合。D(t)为有界函数，则存在常数δ，使得：

|D(t)|<δ。

(41)

4.2 滑模控制器稳定性

为验证本文所设计滑模控制器的稳定性，利用李亚普诺夫函数对所推导系统进行证明[18]。定义李亚普诺函数为：

(42)

则有：

(43)

式中M(q)为正定对称矩阵，即：

(44)

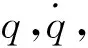
(45)

式(43)可改写为：

(46)

由式(39)可知：

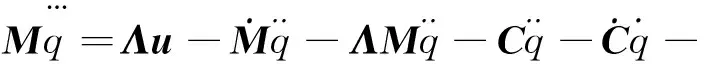
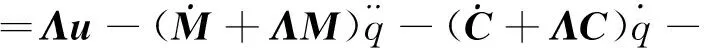
(47)

设计滑模控制律为：

(48)

式中：ψΥ0=H0，H0为精准对象的H;B=diag(B1,B2,…,Bn),Bi>0,i=1,2,…,n;sgn(s)=[sgn(s1),sgn(s2),…,sgn(sn)]。

则有：

(49)

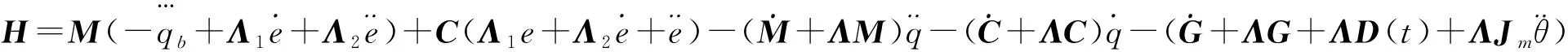
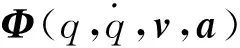
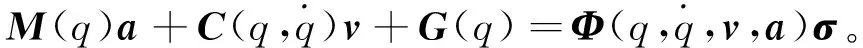
(50)

式中:v表示速度向量，a表示加速度向量。

根据式(50)性质，H可改写为:

(51)

式中Υ为未知向量。

已知i=1,2,…,n，存在第i个向量Υ0i，有：

(52)

式中ϖi>0。

则有：

(53)

(54)

得证，滑模系统相对稳定。

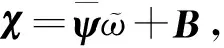
u=-Λ-1[ΨΥ0+χsgn(s)]。

(55)

4.3 滑模控制器参数优化

在滑模控制器设计中，滑模控制参数直接影响控制效果。在滑模面和控制率的设计过程中，要不断地进行参数调整，传统试凑法效率低且很难找到全局最优。随着智能优化技术发展，启发式算法为滑模参数优化提供了新思路。近年来，人工免疫优化算法因分布式并行搜索和全局优化特性而被广泛关注和应用[19]，为此本文引入融合云模型和反向学习的克隆选择算法[20](Clonal Selection Algorithm Combining Cloud Model and Reverse Learning, CSACCMRL)对滑模控制器进行参数寻优。

4.3.1 滑模控制器参数优化模型的建立

锻压机冲击通过机器人底座并经各关节传递到末端执行器形成残余振动，进而影响锻造机器人夹持精度。将锻造机器人末端柔性关节看作二体系统，则其动力学方程为：

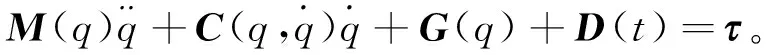
(56)

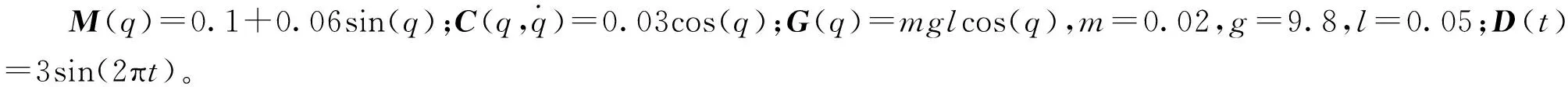
设位置指令r=sin(t)，初始状态x1(0)=0.5，x2(0)=0，设定的目标值x1r=0.5，x2r=0，系统误差e1(t)=x1(t)-x1r，e2(t)=x2(t)-x2r。

设计滑模面

s=c1e1+c2e2。

(57)

式中c1、c2分别为第一、第二误差调节因子。

设计滑模控制率

(58)

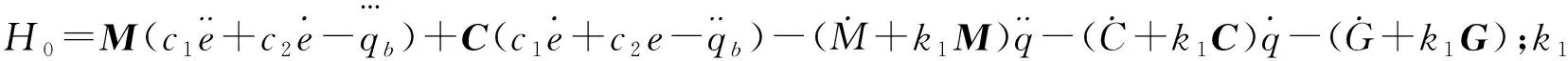
锻造机器人滑模控制器的寻优目标是控制力矩和响应误差尽可能小，基于此建立如下优化模型：

(59)

结合式(58)可知模型优化参数为c1、c2、k1和k2。由试凑法获得参数来确定寻优范围为：c1∈[20,60]，c2∈[50,100]，k1∈[5,45]，k2∈[30,70]。

4.3.2 CSACCMRL的主要算子

CSACCMRL是在引入云模型[21]概念的基础上，使用正向云发生器产生云变异因子对克隆后种群进行变异；利用反向学习策略[22]对变异前后的种群求反向解，实现种群抗体最优选择。其主要算子包括克隆、变异和选择等，相关关系如图4所示。

4.3.3 滑模控制器参数寻优流程

滑模控制器参数寻优具体步骤如下：

步骤1初始化CSACCMRL中种群规模m、优秀抗体规模μ、克隆因子σ、最大进化代数kmax、熵调节因子φ1和超熵调节因子φ2等参数；以及滑模控制器系统中第一、第二误差调节因子c1、c2和比例因子k1、缩放因子k2的寻优范围。

步骤2初始化种群。随机生成包含滑模控制器寻优参数c1、c2、k1和k2的抗体集合A(0)={ai(0)|1≤i≤m}。

步骤3根据式(41)的滑模控制器参数优化模型，计算抗体适应度值并进行升序排序，选出前μ个优秀抗体。

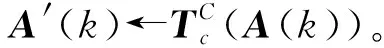
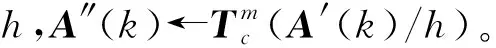
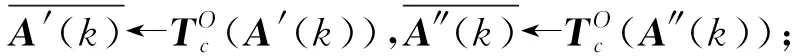
步骤7算法终止判断。若k>kmax，则算法停止并输出最优参数c1、c2、k1和k2；反之k=k+1，转步骤3。

4.3.4 滑模控制器参数优化测试与分析

为了验证CSACCMRL在滑模控制器参数优化中的有效性，在CPU主频3.1 GHz、内存4 GB的PC上使用MATLAB R2018b软件进行测试，并将测试结果与传统试凑法、差分遗传算法[23](Differential Genetic Algorithm, DGA)和自适应混沌克隆选择算法[24](Adaptive Chaotic Clonal Selection Algorithm, ACCSA)进行了比较。试凑法获得的控制器相关参数为c1=30、c2=50、k1=25、k2=50;其余3种启发式优化算法的种群规模均为20，最大进化代数均为1 000。CSACCMRL其余参数取自参考文献[20]测试结果：σ=0.3，μ=10,φ1=3,φ2=10。ACCSA的变异因子为0.1，其余同CSACCMRL。DGA中选择概率为0.08，交叉概率为0.3，变异概率为0.1。鉴于智能启发优化算法的概率性搜索，文中对3种优化算法分别进行了30次独立随机测试，测试结果如表1所示。

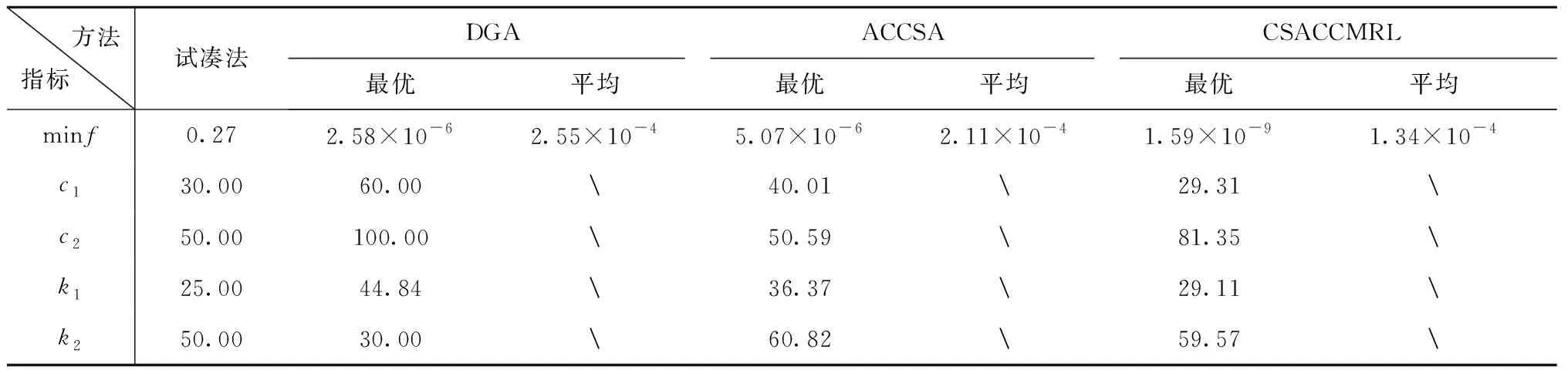
表1 三种算法对滑模控制参数选取结果

由表1可以看出，试凑法效果最差，ACCSA的最优目标值和平均目标值均强于DGA，而CSACCMRL无论最优值和平均值在4种方法中均最小，说明优化效果最好。这主要得益于CSACCMRL在变异环节引入了云模型，通过自适应产生云变异因子来强化其局部搜索能力；在选择操作中加入了反向学习策略，通过对已知解范围外进行搜索，改善了种群多样性，加快了搜索效率，提高了全局优化能力。将4种方法所获得参数应用到滑模控制器中进行仿真测试，各滑模控制器响应对比如图5所示。

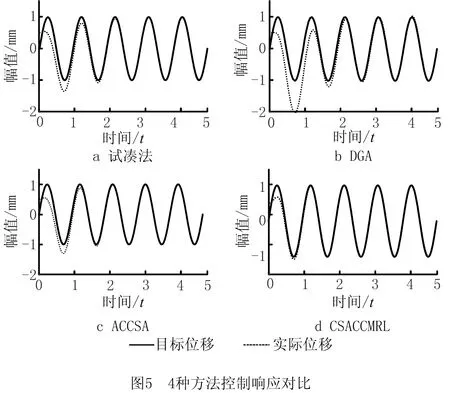
由图5可以看出，与传统试凑、DGA和ACCSA所获得滑模控制器响应相比，CSACCMRL实现了滑模控制器对外界干扰的快速抑制，且稳定时间相对提高75.0%、66.7%和37.5%，平均误差相对减少50.7%、28.7%和14.4%，说明了CSACCMRL在滑模控制器参数优化中的有效性。

5 残余振动抑制设计与试验

为了进一步验证本文开闭环混合控制的残余振动抑制策略有效性，基于MATLAB/Simulink仿真平台构建如图6所示的锻造机器人残余振动抑制仿真模型，仿真时间为5 s。模型输入端首先施加了正弦跟踪输入信号。为了更好地模拟锻造环境，使得数值测试更能贴近实际，在模型输入端还增加了幅值为0.1的白噪声，以及在0.2 s和3.2 s处增加了幅值为0.6的脉冲信号来代替外界干扰。基于本文抑制策略，采用ZVD输入整形器对锻造机器人柔性臂的输入信号进行整形，并传输到滑模控制器。滤波器作用下，将滑模控制器自身的高频抖动清除，同时抑制外部干扰，实现锻造机器人的精确运动控制。

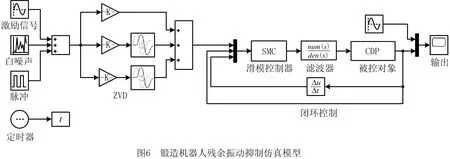
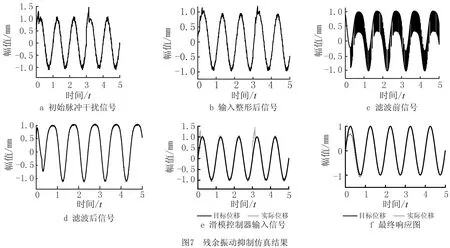
如图7所示为残余振动抑制仿真结果。图7a给出了含有白噪声和脉冲振动的外界干扰信号;图7b显示经过输入整形器整形后，外界干扰信号的最大幅值消减到目标值附近，信号幅值减小了45.7%;由图7c和图7d可以看出，滑模控制器自身的抖振频率高、幅值大严重影响滑模控制器的效果，而通过在滑模控制器和锻造机器人系统之间加入低通滤波器，可以消除滑模控制器自身92.1%的抖振;图7e给出了滑模闭环控制的输入信号和期望信号;图7f为锻造机器人系统输出，且响应在0.2 s内到达目标值，滑模控制器对含脉冲的外界干扰信号平均抑制达98.4%，进一步验证了本文基于输入整形和滑模控制的锻造机器人残余振动抑制的有效性、快速性。

6 结束语

针对锻造机器人的残余振动，本文提出了基于输入整形和滑模控制的锻造机器人残余振动抑制策略。基于数值测试结果分析可以得出如下结论：

(1)引入输入整形器到锻造机器人开环控制系统中，将给定冲击信号与特定脉冲序列进行卷积，能实现残余振动的大部分幅值初始有效抑制。

(2)在锻造机器人闭环控制系统中引入滑模控制器，能够通过系统反馈进行调整，降低外界扰动对系统的影响。而通过在滑模控制器中加入滤波器，则能有效解决控制器自身抖振问题。

(3)为了解决滑模控制器参数选择对残余振动抑制的影响，利用智能克隆选择算法对锻造机器人滑模控制器优化模型进行参数寻优，能实现滑模控制器对外界干扰的快速抑制，提高稳定速度。

(4)融合输入整形和滑模控制的锻造机器人残余振动抑制混合策略，能实现白噪声和脉冲的外界干扰有效和快速抑制。

恶劣的锻造环境使得锻造机器人生产线已经成为提高锻造生产安全和效率的亟需，但锻造车间内工作的锻压机不可避免地会产生高频的振动，且会通过地基传递给锻造机器人造成残余振动，进而影响锻造机器人的抓取精度，因此如何抑制振动提高是锻造机器人控制精度的难点，文中融合输入整形和滑模的振动抑制策略提出将有助于解决该技术问题。但目前已有研究主要是建立在锻造机器人数字模型上，下一步研究主要是将振动抑制策略成果应用到实际锻造机器人本体上进行工程可行性和有效性的进一步验证，从而切实提高锻造机器人的控制精度。