基于双层规划的云制造资源服务组合
2022-02-19潘燕华
王 平,肖 涵,2+,潘燕华
(1.江苏科技大学 经济管理学院,江苏 镇江 212003;2.镇江市高等专科学校 现代装备制造学院,江苏 镇江 212028)
0 引言
云制造[1]融合广泛地域中海量资源为各类制造需求提供丰富的定制化服务,实现制造无缝衔接、资源互通共享的优化协同[2]。云制造模式的应用能够为制造企业拓展制造能力,拓宽制造范围,降低运营成本,提高社会资源的综合利用率,并最终实现多方共赢[3]。然而,随着云制造技术的快速发展,以及制造任务的日益复杂,单一的云服务已经难以满足需求者的任务需求,因此云制造平台需要通过云制造服务组合来满足复杂的制造需求[4]。如何在大量功能相同但质量参差不齐的制造资源中为服务需求方构建出既能满足需要,且综合质量最优的服务是云制造领域面临的难题[5]。
目前,对云制造服务组合的研究主要集中在评价指标体系、评价方法以及智能化算法等方面。
(1)评价指标体系方面 贺可太等[6]从需求方利益和风险两方面建立了服务质量评价指标体系;吴艳霞等[7]在服务质量的基础上增加了知识贡献度、服务评价和使用优先级;蔡安江等[8]构建了以时间、成本、可用性、准确性、创新性、可信性为优化目标的服务组合优化模型;徐宣国等[9]建立了云服务组合柔性的四维属性测度评价指标体系。
(2)评价方法方面 赵道致等[10]建立了基于需求方服务质量和平台柔性的多属性资源分配的双层结构优化决策模型;丁涛等[11]从资源服务、功能服务和流程服务3个层次构建了服务组合优选的质量评估模型;陈友玲等[12]以需求方和供应方为基础,建立了服务组合综合评估双层约束模型;吴艳霞等[7]构建了云制造平台可持续性最强、供应方服务质量最优的双层规划模型。
(3)智能化算法方面 陈友玲等[13]提出一种基于反向和局部学习的蚁群算法,求解并行制造云服务的组合优化问题;郑炜等[14]采用双层蚁群算法解决云服务组合后灵活度降低、解空间被限制等问题;金鸿等[15]利用教—学算法求解云服务组合整体服务质量最优组合;朱李楠等[16]结合云制资源组合的跨地域高度分散性的特征,设计了改进的差分进化算法对资源组合进行求解。
服务组合优化是云制造中构造松耦合敏捷制造方案、实现资源优化配置的关键技术[17],现有研究已取得了丰硕成果,但仍然存在一些不足:现有研究大多依据时间、成本等QoS指标,忽略了资源供应方的生产能力对云制造平台资源组合的影响;多数学者从云制造的某一方或供需双方的视角构建模型,忽略了云制造平台在资源优化配置过程中的作用;问题求解过程中忽略了大量的模糊性和不确定性评价信息。本文在现有研究的基础上,提出了基于双层规划的云制造资源服务组合优选模型。该模型将供需双方同时作为上层决策者,利用前景理论计算服务需求方对资源供应方的满意度,并以时间、质量、成本、信誉度为约束条件,实现服务质量最优;以云制造平台作为下层决策者,供应方的剩余负载及需求方的满意度作为约束条件实现资源利用率的最大化,并采用结合云模型中云滴的确定性和稳定性[18]而设计出的云遗传算法对该双层规划模型进行求解。
1 云制造资源服务组合评价指标体系
1.1 评价指标体系构建
基于现有云环境下制造资源服务组合评价指标体系,本文构建了涉及服务需求方、资源供应方和云制造平台三方的双层规划模型(如图1)。双层规划模型[19]是一种上下层拥有各自目标和约束条件的主从决策优化模型[20],可以很好地解决云环境下制造资源服务组合优选问题。
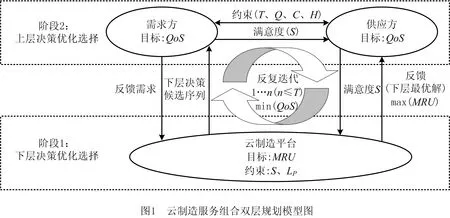
通过构建双层规划模型图,可以清晰地了解所构建的双层规划模型中各层的决策主体以及目标函数、约束条件和上下层之间的关系。图1中上层决策主体为需求方和供应方,下层决策主体为云制造平台。下层模型的优化目标为资源利用率MRU,约束条件为供应方的剩余负载LP与需求方对供应方的满意度S,计算出最优MRU的排名,下层模型最为优先决策层,将结果反馈至上层决策主体,上层模型的优化目标为服务质量QoS,约束条件为时间T、成本C、交付物质量Q,信誉度H。上、下层之间相互制约又相互依赖。评价指标的具体描述如表1所示。

表1 云制造服务组合评价指标
1.2 制造资源服务满意度求解
前景理论以决策者有限理性为前提,能够较好地刻画决策者的心理行为特征[23]。该理论利用实际值rij与参照点eij之间的距离作为衡量满意度大小的依据,根据评价指标不同的属性(即成本型或效益型)计算各指标的损益值[24]。利用前景理论计算服务需求方对资源供应方的满意度,不但可以增加供需双方匹配的约束条件,而且有利于资源匹配完成后,供需双方对制造任务的配合,提高云制造平台的工作效率,具体计算如下:
(1)计算各待选资源时间(t)、成本(c)、交付物质量(q)、信誉度(h)的实际值rij与其各自参照点eij(需求方的最低要求)之间的距离dij,
dij=|rij-eij|。
(1)
(2)计算各待选资源针对不同指标的损益值。
(2)
(3)
(3)计算各待选资源的前景值并进行归一化处理。
(4)
(5)
(6)
其中:α,β(0<α,β<1)表示不同的风险敏感系数,取值越大,决策者对风险越敏感;λ(λ>1)表示决策者损失规避系数,取值越大,决策者对损失的规避意愿越强烈。
(4)求解各待选资源的满意度S,
(7)
式中ωj表示各指标前景值所对应的指标权重。
1.3 制造资源服务组合QoS求解
云制造环境下的服务组合主要包括串联、循环、选择、并行4种结构。串联结构是最基础、最重要的服务组合形式,其余3种结构均可以简化,等效为一个独立的制造服务环境,与其他部分组成串联结构的服务组合[25]。因此,本文以串联结构作为云服务组合研究对象。
(1)总时间最少
(8)
式中:ti为子任务i的候选制造资源加工时间;n为子任务数。
(2)总成本最小
(9)
式中:ci为子任务i的候选制造资源加工成本;n为子任务数。
(3)交付物质量最优
(10)
(4)信誉最优
(11)
式中:5表示信誉度的最高评价值,其取值范围在1~5之间;n为子任务数。
(5)QoS计算
采用线性加权方法将QoS的多目标函数转化为单目标优化函数:
(12)
式中:ωT、ωC、ωQ、ωH分别为时间、成本、交付物质量、信誉度的权重;T′max、C′max分别为需求方能够接受的最长时间、最高价格;Q′max=1-Q′min、H′max=5-H′min,Q′min、H′min分别为需求方最低交付物质量要求、最低信誉度。
1.4 制造资源利用率求解
云制造平台在进行服务资源匹配时,需要考虑资源供应方的剩余工作能力,即剩余负载,优先选择剩余负载与需求负载相接近的资源作为候选资源,从而提高平台资源的利用率,同时保证云制造平台工作效率和服务质量。制造资源的利用率为:
首先,要求现有在职学生管理人员充分认识到信息技术已成为了信息时代对高校学生管理工作最基本的能力要求,只有具有相应的信息技术,才能做好大学生管理工作。其次,通过开展辅导员沙龙等形式,为教师间搭建良好的交流平台,促进学生管理队伍大数据分析能力的有效提升。最后,通过开展讲座、报告及交流等活动,促进高校学生管理团队多媒体操作技能与学生管理信息化系统管理能力的全面提升。
(13)
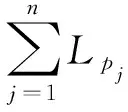
2 云服务组合双层规划模型构建
2.1 数学模型
在确定供需双方满意度后,建立以服务质量为目标函数的上层优化模型,以及考虑最大资源利用率的下层优化模型,具体云服务组合优化数学模型为:
(U)
min (QoS)。
s.t.
T′max≥T;
C′max≥C;
(L)
max (MRU)。
s.t.
Smin≤Si,i=1,2,…,n。
(14)
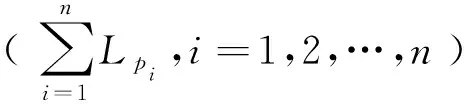
2.2 云服务组合双层规划模型求解
2.2.1 云遗传算法
双层规划问题非凸性、非连续性的特征,导致该模型具有高度的不确定性,对其进行求解是一种强NP难问题。虽然遗传算法是一种全局优化搜索算法,但它不在单点上寻优,而是在整个解空间寻找全局最优,局部搜索能力差,搜索速度慢且容易发生提前收敛现象[27],交叉与变异的概率不能对实际云环境下的服务组合的不确定性进行准确描述。云遗传算法[28](Cloud Genetic Algorithm,CGA)的基本思想是利用云模型云滴的随机性和稳定倾向性特点,保持个体多样性从而避免搜索陷入局部极值,并且可以很好地保护较优个体对全局最值进行自适应定位[29],结合遗传算法交叉变异思想,由云模型的Y条件云生成算法实现交叉操作,基于云发生器实现变异操作[30],完成进化过程。
算法1CGA交叉概率Pc生成算法[28]。
E′n=norm(En,He) ,
(15)
算法2CGA变异概率Pm生成算法[28]。
E′n=norm(En,He) ,
(16)
2.2.2 算法流程
(1)首先,利用前景理论(式(1)~式(7))计算出各候选服务资源的满意度,然后对候选资源服务组合进行编码,例如MR1,2-MR2,3-MR3,3-MR4,1-MR5,2,其对应的十进制编码为{2-3-3-1-2}。
(2)种群初始化。设定种群初始规模为N,最大迭代次数为I,生成初始种群P(0)。
(3)适应度计算。将下层目标函数max(MRU)转化为适应度函数,计算每个制造资源个体的适应度。
(4)确定选择算子。采用轮盘赌法,按照制造资源适应度大小进行排序,从种群P(t)中选出满足下层约束最优的候选制造资源,复制到下一代种群P(t+1)中。
(5)交叉算子操作。利用算法1,其中C1=C2=0.6,k1=k2=0.9,生成交叉概率Pc(t) ,采用一点交叉对群体P(t)的个体进行交叉操作。
(6)变异算子操作。利用算法2,其中C3=C4=0.1,k3=k4=0.5,生成变异概率Pm(t),对群体P(t)中的个体进行变异操作。
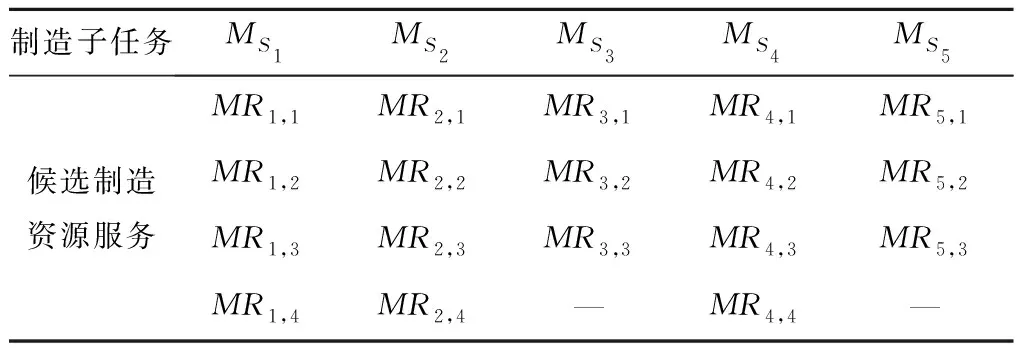
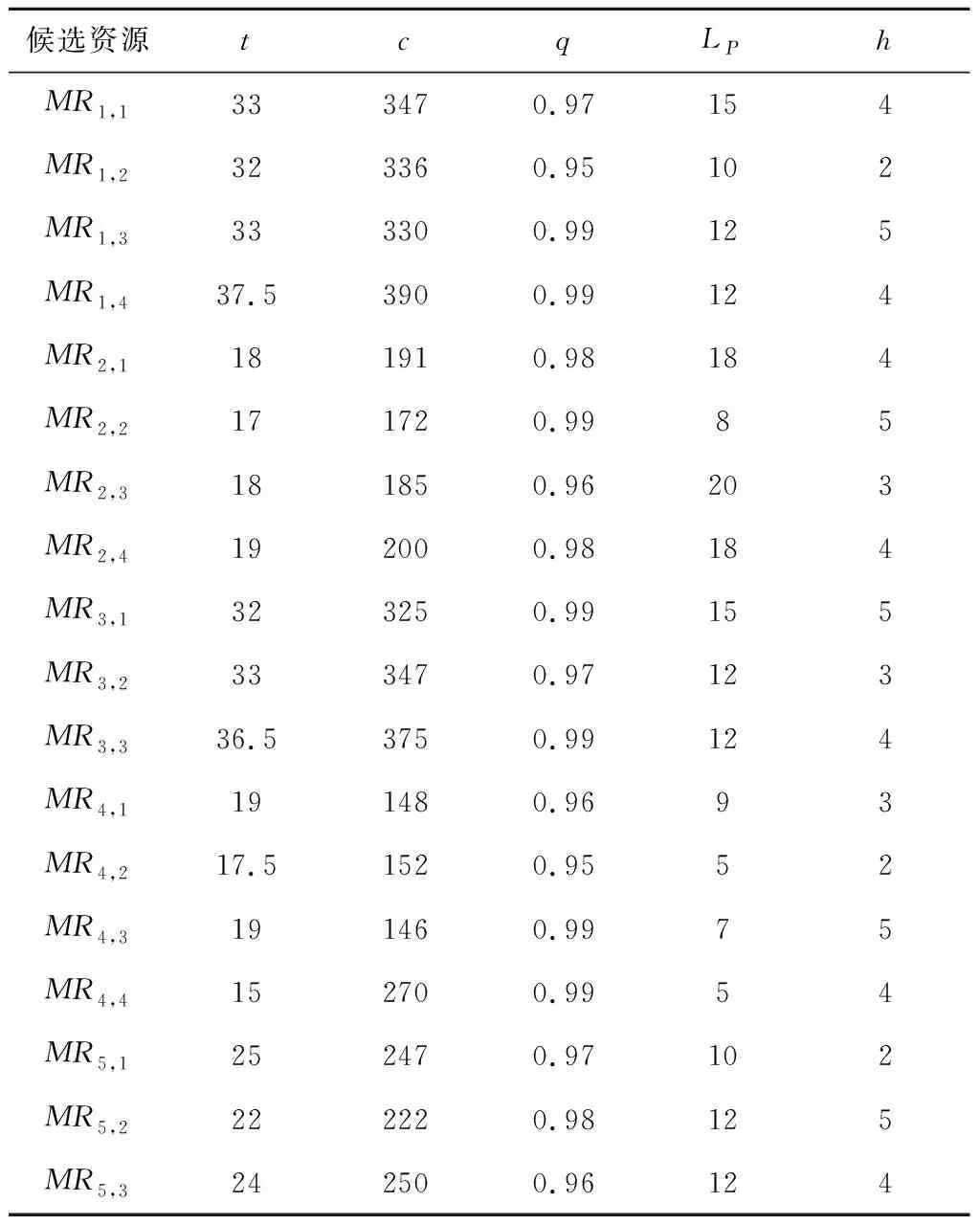
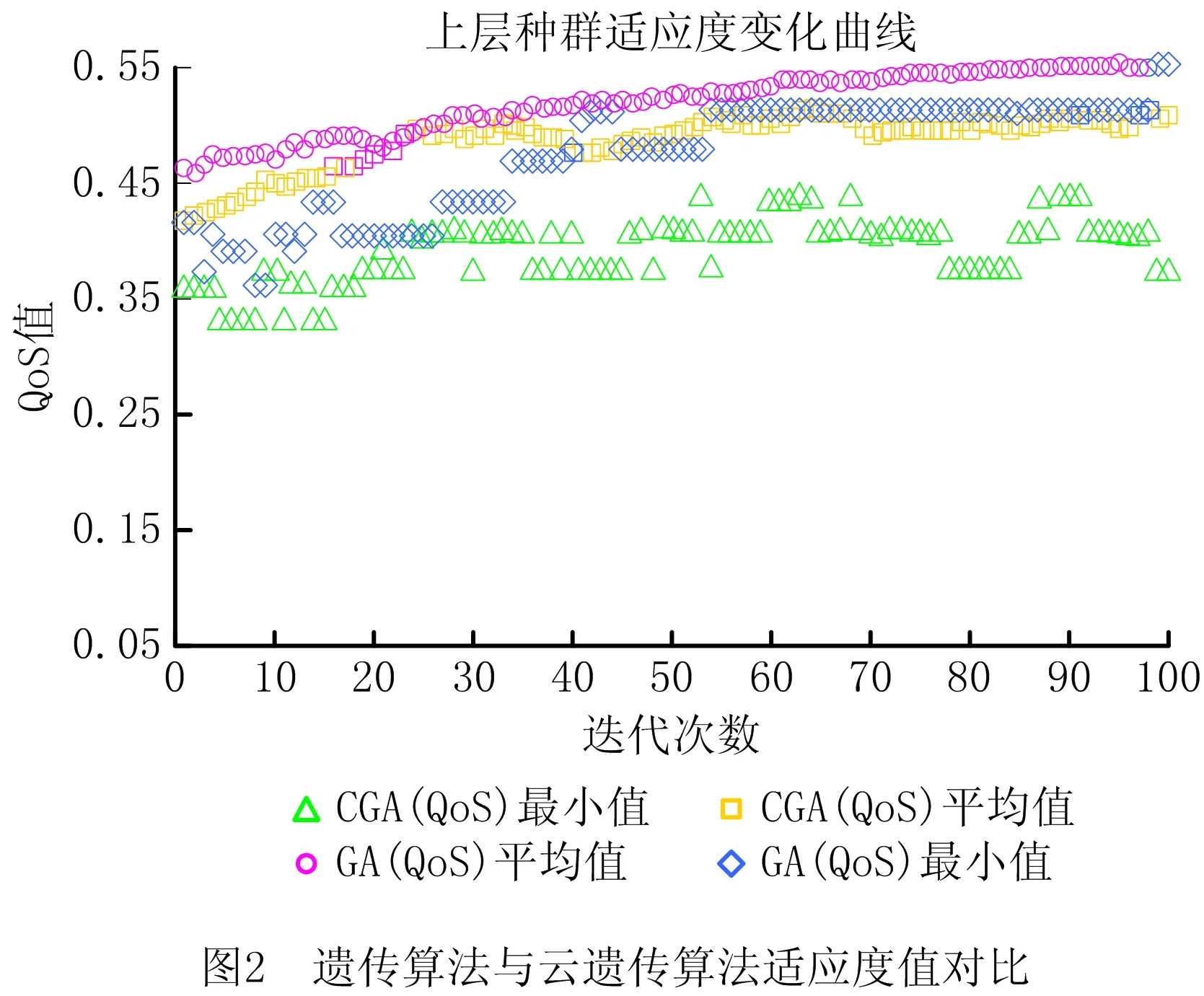
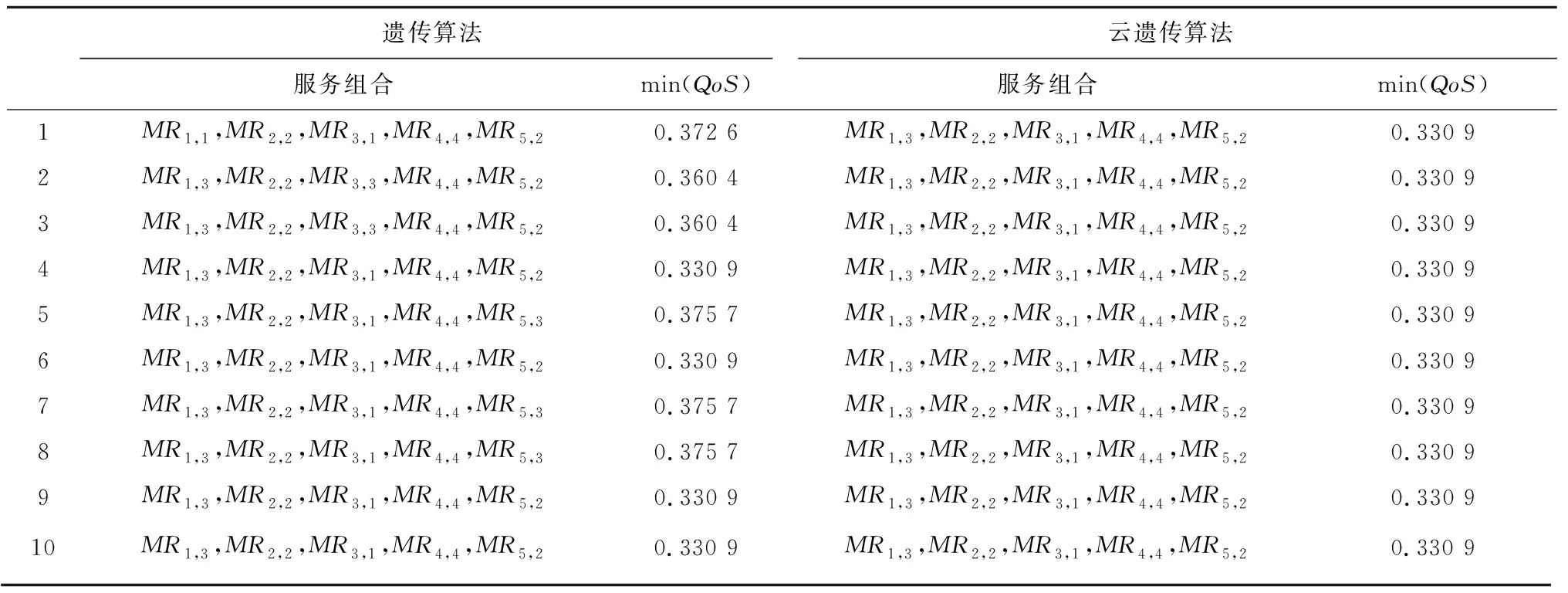
(7)判断终止条件。P(t)经过遗传算子操作(选择、交叉、变异)产生新群体P(t+1),若t≥T,则进化过程中所得到的具有最大适应度的个体作为最优解,代入下层规划目标函数,更新目标函数值,输出结果;若t (8)将步骤(7)输出的解集作为上层目标函数的可行解,分别计算各个可行解,选取QoS最优即min(QoS)的制造资源组合方案。 某企业在云制造平台发布了一项制造任务Ta,并提交需求(如表2)。云制造平台将制造任务Ta分解为5个子任务,Ta={MS1,MS2,MS3,MS4,MS5},如表3所示。云制造平台经过初步筛选,选出符合制造子任务的候选制造资源MRi,j,候选资源指标相关参数如表4所示。云制造平台通过对子任务候选资源的优选,实现制造任务服务组合最优。 表2 需求方相关需求 表3 候选服务资源 表4 候选资源评价指标相关参数 根据以上模型所需要的参数,Tmax=300,Cmax=2500,Qmin=0.95,Hmin=3,Ld=40,Smin=0.46以及ωt=0.3,ωc=0.25,ωq=0.25,ωh=0.2,结合式(12)~式(14)可得算例双层规划模型: (U) min(QoS)=min s.t. T≤300; C≤2 500; qi≥0.95,i=1,2,…,5; hi≥3,i=1,2,…,5。 (L) s.t. S≥0.46。 (17) (1)满意度计算 利用前景理论,以各正、负指标理想数值作为参照点,利用式(1)~式(7)计算服务需求方对各个候选制造资源的满意度,计算结果如表5所示,其中α=β=0.88,λ=2.25。 (2)算法验证 利用2.2.2节算法流程对式(17)进行求解,取初始种群N=50,最大迭代次数I=100。如图2所示,绿色和红色分别表示云遗传的最小适应度值和平均适应度值,紫色和黄色分别表示遗传算法的最小适应度值和平均适应度值。由于关于QoS的模型求解以求解最小值为最优值,从图中可以看出,运用云遗传算法计算的的QoS平均适应度与最小适应度值在100次的迭代过程中,均小于云遗传算法的QoS值,因此,运用云遗传算法求解的种群平均适应度值和最优适应度值均比传统遗传算法的适应度值更优化,并且在100代的计算中可以看出,云遗传算法的最优适应度具有更好的多样性和随机性,能够很好地避免算法陷入局部最优解,不易收敛;而传统遗传算法在第50代左右出现收敛。 表5 需求方对各制造资源满意度 为了证明模型算例的有效性,采用穷举法计算云制造资源服务组合的最优解为min(QoS)=0.330 9,服务资源组合为MR1,3-MR2,2-MR3,1-MR4,4-MR5,2。同时分别对传统遗传算法与云遗传算法的10次迭代运算结果进行对比,如表6所示。 由表6的对比结果可知,云遗传算法10次迭代运算输出结果均为最优解,具有稳定性,而传统的遗传算法10次迭代输出结果仅出现4次最优解,相对于云遗传算法,缺少了一定的稳定性。因此,本文的模型算法优化了传统算法搜索全局最优解的能力。 表6 遗传算法与云遗传算法结果对比 本文以前景理论求解出的需求方对供应方满意度为前提,综合考虑需求方、供应方以及云制造平台三方利益,构建了上层以服务质量为目标函数,下层考虑资源利用率最大化的制造资源服务组合双层规划模型;基于云制造环境下该模型的不确定性及随机性等问题,采用具有稳定倾向性的云遗传算法进行数据求解,并将计算结果与穷举法、遗传算法进行对比。结果表明,所提模型及求解算法可以高效、准确地解决云制造资源服务组合问题,研究结果能够为云制造服务平台的建设供应方法参考和实践支持。下一步,将考虑针对云制造资源个性化服务需求与配置的模型优化问题进行深入研究。3 应用分析
3.1 案例设计
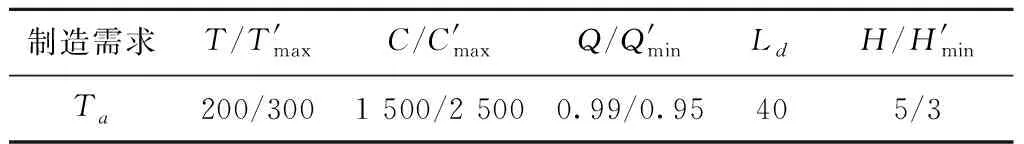
3.2 算例求解

3.3 结果对比分析
4 结束语
