面向云制造协同创新伙伴选择的多源异构VIKOR群决策方法
2022-02-19周向红李丹萍成鹏飞喻维纲傅呈勋
周向红,李丹萍,成鹏飞+,喻维纲,傅呈勋
(1.湖南科技大学 商学院,湖南 湘潭 411201;2.产业发展大数据与智能决策湖南省工程研究中心,湖南 湘潭 411201;3.湖南华菱湘潭钢铁有限公司,湖南 湘潭 411101)
1 问题的描述
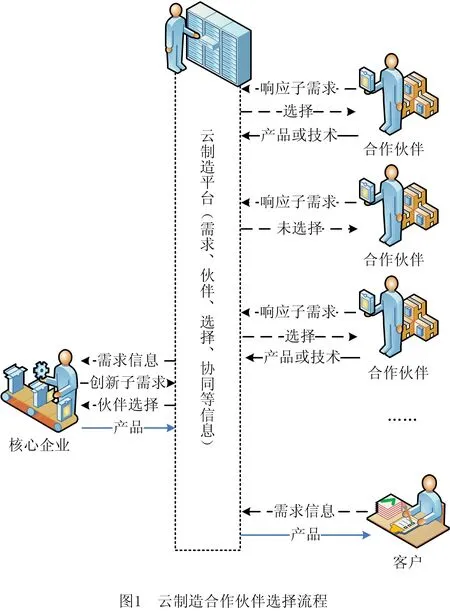
数字技术已深刻影响新时代社会和经济的发展,面对多样化、个性化的用户需求和激烈的市场竞争,单个企业的资源和能力难以适应快速变化的市场机遇[1],因此借助数字技术整合不同资源以共同拓展市场的虚拟企业应运而生[2]。云制造是一种面向服务、高效低耗和基于知识的网络化制造新模式,它融合了制造、云计算、物联网、语义Web、高性能计算等技术,将各类制造资源与能力进行虚拟化、服务化,并进行统一、集中的智能化管理和经营,为用户提供随时可取、按需使用、安全可靠、优质价廉的服务[3]。可见,云制造是一种快速响应市场需要的虚拟企业,主要由核心企业、合作伙伴和客户构成,如图1所示。核心企业是合作伙伴选择的主导者,借助云制造平台直接响应客户需求,协调多个合作伙伴共同完成制造任务。由于核心企业面临云端多样化的制造需求,尤其是针对一些技术开发难度大的个性化制造项目,需要利用云制造平台快速整合具有创新资源的合作伙伴(即协同创新伙伴),相应地,协同创新伙伴也需要依托云制造平台实现与核心企业创新需求的快速精准匹配。通过多主体间分工合作,弥补核心企业在某些专业领域内能力欠缺、研发周期长和成本过高等不足,以快速完成制造任务,因此,如何选择协同创新伙伴是云制造模式中需重点研究的问题[4-5]。核心企业应根据客户个性化需求,选择最佳的协同创新伙伴,以提升创新速度,提高创新资源投入产出效率,增强整体创新能力[6-7];但云制造受企业地域分散、合作网络动态化,以及创新的不确定性等因素的影响,客观准确了解候选协同创新伙伴成为一个现实难题,不合适的合作伙伴往往会导致协同创新风险[8]。由云制造过程可知,伙伴选择处于协同创新开展之前,是云制造实施的重要条件,也是云制造的关键环节,在一定程度上决定了协同创新的最终结果[9]。因此,开展云制造模式下协同创新伙伴选择决策研究,有利于核心企业高效建设动态的创新组织,快速响应市场需求,提升云制造创新效率与水平,对推动制造业高质量发展具有重要的实践指导意义。
目前,国内外学者对合作伙伴的选择进行了大量研究,主要集中在评价指标体系和评价方法两个方面。
(1)评价指标体系 针对云制造模式下企业合作伙伴选择问题,已有文献从成本、时间、质量、风险和信誉等方面对合作伙伴选择进行了研究[10-12],还有学者考虑了安全性和协同性等指标[13]。针对企业合作创新伙伴选择问题,有文献从资源能力、管理能力、技术能力状况、产权信誉、兼容程度、双方合作动机的一致性等方面建立了创新伙伴选择指标体系[14-16],也有从知识拥有和管理经验、技术能力、资源互补等主观准则对合作创新伙伴选择进行评价[17]。通过文献梳理发现,针对云制造模式下协同创新伙伴选择的指标体系研究明显不足,现有指标体系中未考虑创新伙伴与核心企业之间的互补适宜程度、云制造平台接入的便利性以及云制造参与次数。
(2)评价方法 YE[18]针对信息不完整和不确定环境下的合作伙伴选择问题,提出了基于扩展TOPSIS(technique for order preference by similarity to an ideal solution)法和区间直觉模糊决策。TAO等[19]在考虑最小成本和风险、最大质量和柔性的基础上,提出一种GA-BHTR(genetic algorithm maintained using the binary heap and transitive reduction)算法选择合作伙伴。AMID等[20]建立了模糊多目标线性模型,应用模糊决策方法对合作伙伴进行择优评价。OPRICOVIC[21-22]提出了解决复杂系统评价问题,能够获得折衷解的VIKOR多属性决策方法。国内学者康艳芳等[23]利用灰色关联综合评价模型建立了云服务市场优化指标,并运用多目标优化模型对选择提供云服务合作伙伴进行了定量研究。张敏等[24]采用TOPSIS法处理评价值为区间数的企业伙伴选择问题。张树山等[25]提出了考虑模糊信息和不确定性因素的协同创新合作伙伴FAHP-TOPSIS(fuzzy analytical hierarchy process-TOPSIS)组合评价方法。邵明晖等[26]利用直觉模糊集TOPSIS法选择协同创新合作伙伴。姚升保[27]提出一种集成模糊逻辑、网络分析法和多准则折衷优化解法(Vise Kriterijumska Optimizacija Kompromisno Resenje, VIKOR)的模糊组合决策方法,解决产业技术创新联盟合作伙伴选择的决策问题。云制造协同创新伙伴评价指标体系包括主观和客观两大类,而评价信息具有多源异构性,且数据彼此间存在不可公度性[28]。与传统的多属性决策方法相比,VIKOR方法在解决数据间不可公度性、获得妥协最优解方面具有较大优势。目前,VIKOR方法已被用于解决多准则决策问题[29-32],将VIKOR方法推广到区间值环境[30]、犹豫模糊语言环境[33]。可见,有关合作伙伴选择的方法和模型的研究成果较为丰富,但大多仅考虑单一的评价信息,涉及多源异构评价信息的研究较少,缺乏具体结合云制造模式的协同创新合作伙伴选择方法。
综上所述,现有研究还存在以下局限:①云制造模式下协同创新伙伴评价指标还不够完善,针对性不强,没有考虑协同创新伙伴与核心企业的相容性、协同创新伙伴的创新能力、创新项目的技术方案,以及创新效果等众多要素的影响;②现有合作伙伴选择评价方法处理的评价信息过于单一,未考虑协同创新伙伴评价信息的多源异构性,即信息来源于核心企业决策者、合作伙伴或云制造平台等不同主体,评价信息度量形式各异,可能是实数、区间数、语言值等多种结构形式;③现有文献指标权重计算大都采用单一赋权方法,而未考虑主客观相结合的综合赋权,导致决策结果的不确定和不准确,不能满足云制造的实际决策需要。
本文针对云制造模式下协同创新伙伴选择评价指标体系不完善、指标权重难以合理确定、多源异构评价信息不可公度、集结难等问题,拟设计科学全面的评价指标体系,通过最优最劣法(Best-Worst Method, BWM)与熵权相结合的主客观综合赋权方法,构建一种面向云制造协同创新伙伴选择的多源异构VIKOR群决策方法。
2 基础理论
2.1 区间数
定义1[34]设a=[aL,aU],aL≤aU,定义为实轴上的区间数,aL和aU分别表示a的上界和下界。
定义2令a=[aL,aU]和b=[bL,bU]为两个区间数,则a和b之间的欧式距离[35]
(1)
2.2 中智数
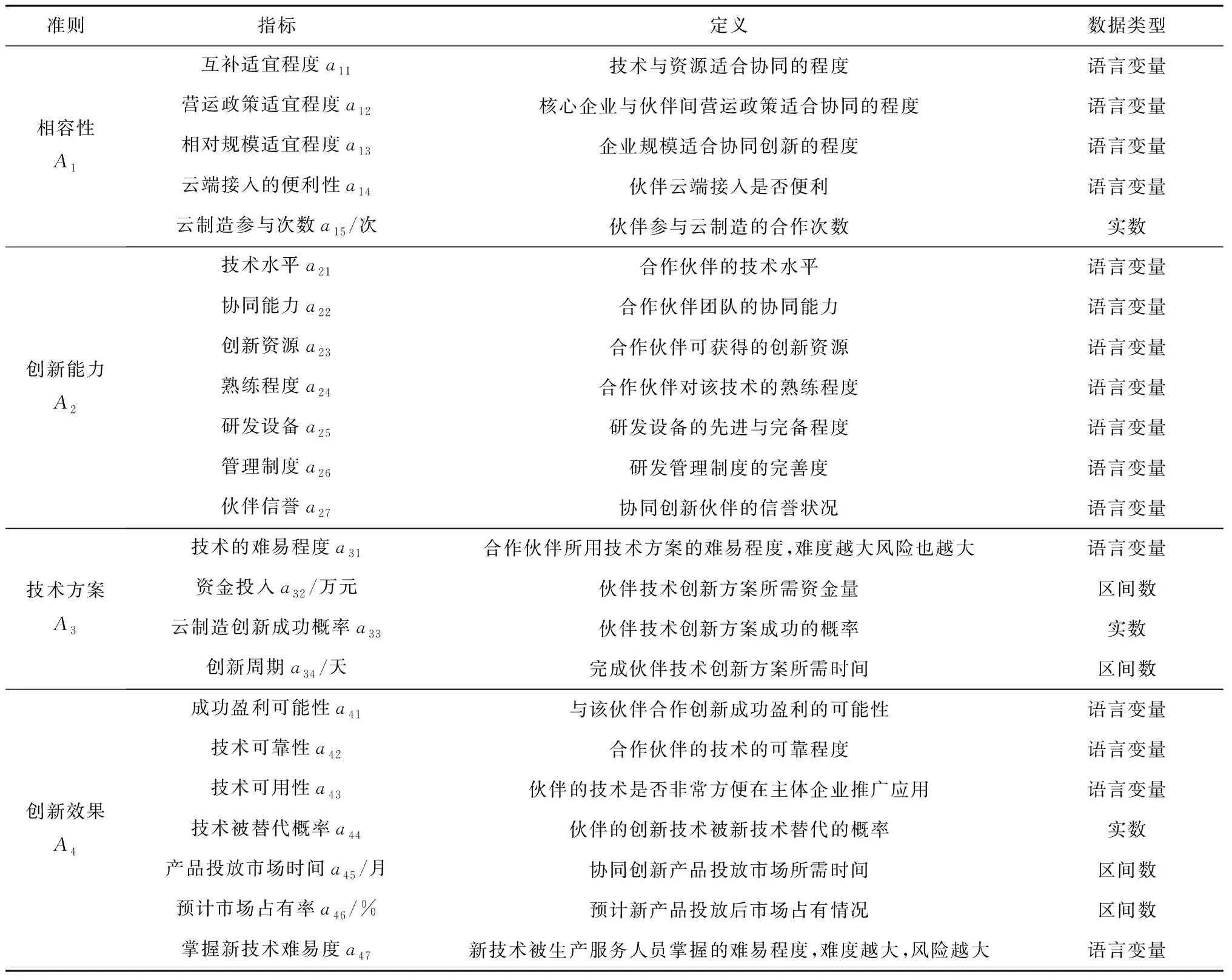
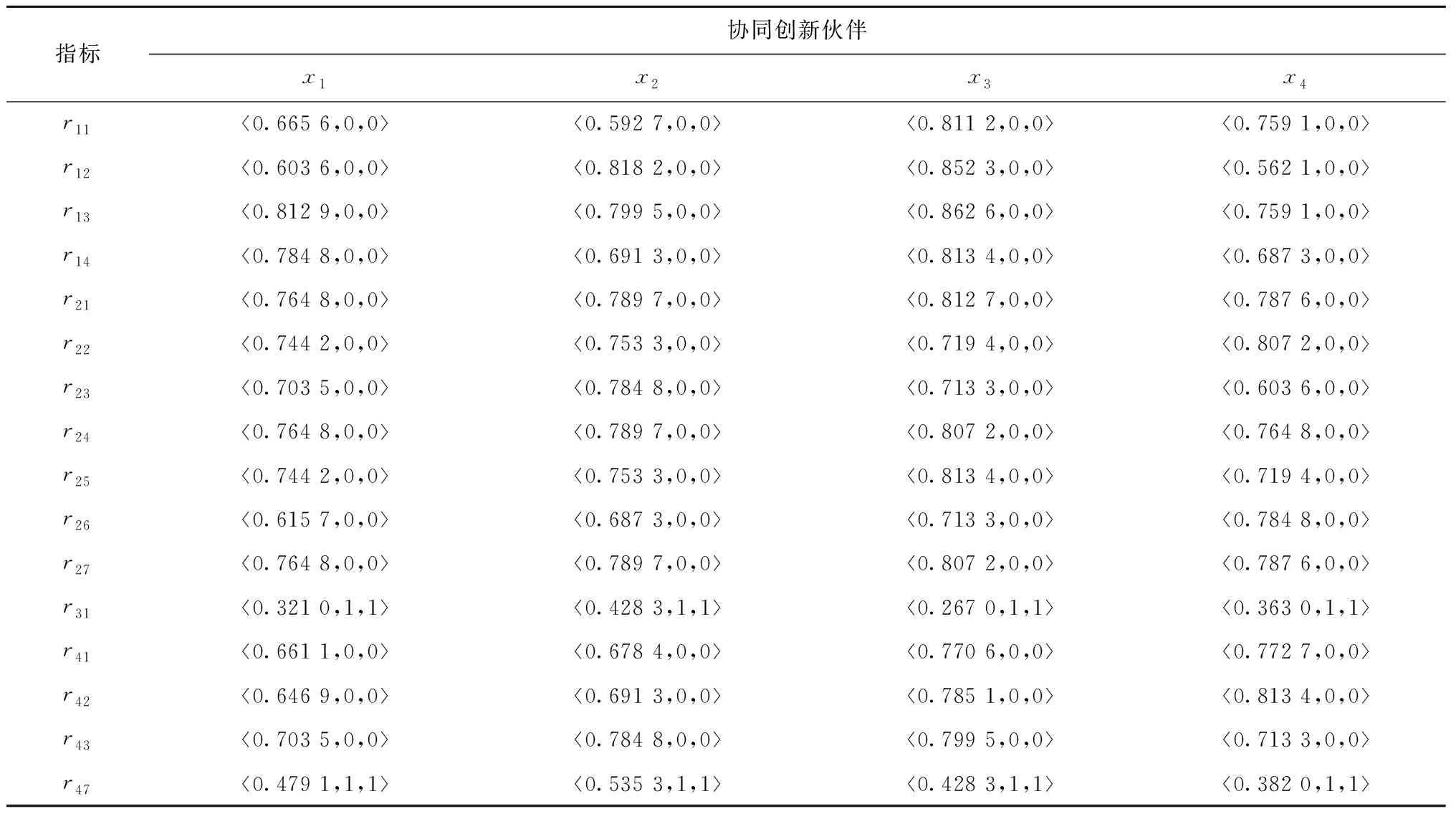
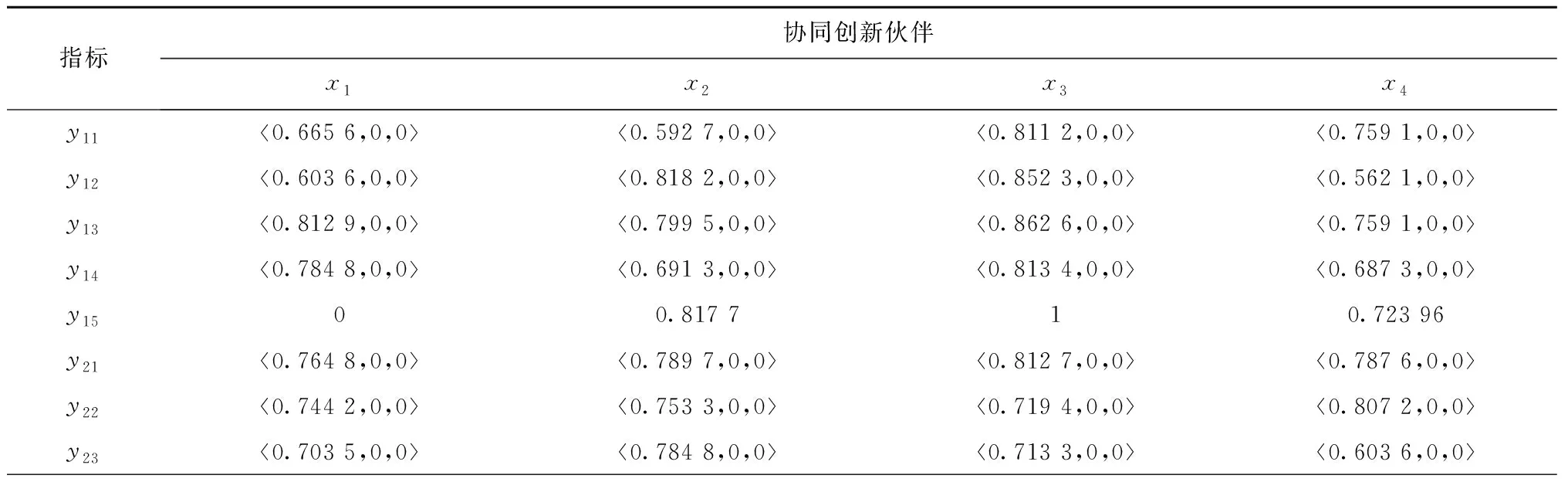
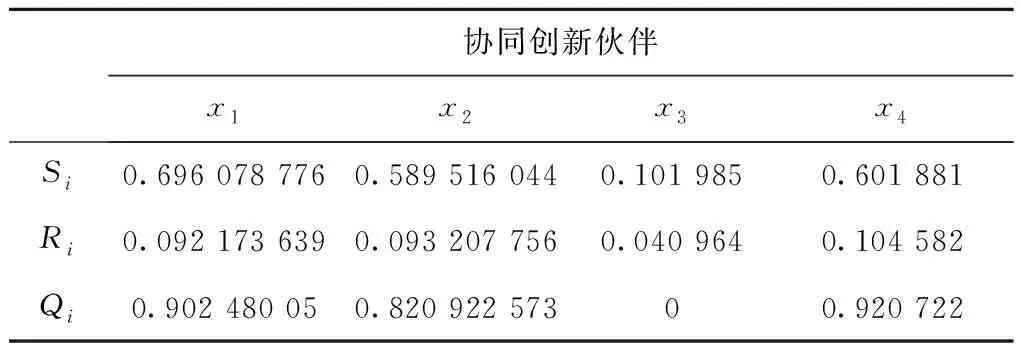
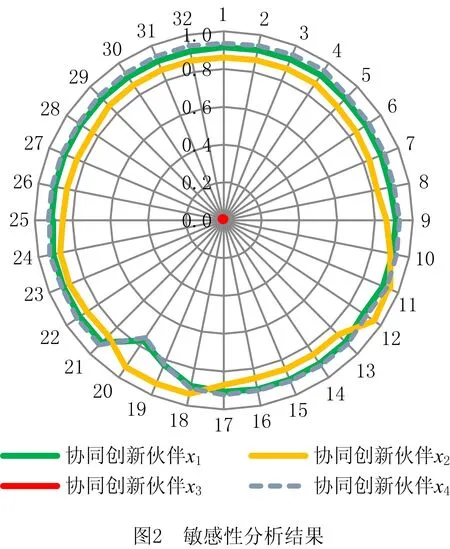
定义3[36]设X为对象集,x为其中任意一个元素,X上的一个中智集A可以由真实程度函数TA(x)、不确定程度函数IA(x)及谬误程度函数FA(x)表示,可以表示为A={〈x,TA(x),IA(x),FA(x)〉|x∈X},其中TA(x),IA(x)和FA(x)是[0,1]的标准或非标准实数子集,即TA(x):X→[0,1],IA(x):X→[0,1],FA(x):X→[0,1],0 (2) 定义6[39]设X=(x1,x2,…,xn),中智集A={〈x,TA(x),IA(x),FA(x)〉|x∈X},则A的中智熵 FA(xi))⊗|IA(xi)-IAc(xi)|。 (3) 其中AC为A的补集。熵表示属性值的不确定,熵越大,不确定性越大,则熵权 (4) 定义7[40]设X=(x1,x2,…,xn),中智集A={〈x,TA(x),IA(x),FA(x)〉|x∈X},则单值中智加权算术平均算子 WAψ(A(x1),A(x2),…,A(xn)) =ψ1A(x1)⊕ψ2A(x2)⊕…⊕ψnA(xn) (5) 云制造环境下,核心企业的研发与制造任务有两种来源:①在云制造平台上客户定制化需求,属于市场拉动型,具有被动性;②通过市场调研与分析,了解到未来一段时间某类产品会有较大市场需求,核心企业预先组织研发生产,属于生产推动型,具有主动性。通常而言,云制造模式中,第①种来源更常见,其时间更紧迫。但不管何种来源,由于核心企业自身创新能力和条件的局限性,无法在短时间内独自完成全部研发与产品生产,并投放市场[1],因此需要借助云制造平台寻找合适的协同创新伙伴,缩短研发时间,提升研发质量,快速满足市场需求。 核心企业根据客户需求确定产品结构和功能后,将产品研究与制造划分为多个子任务,细化确定各子任务的QoS(quality of service)需求,并向云制造平台提交带有QoS约束的服务请求[41]。云制造平台收到请求后,首先根据各子任务功能要求,筛选符合核心企业要求的候选协同创新伙伴,然后通过核心企业决策者、领域专家和云制造平台等多个来源收集候选协同创新伙伴的评价信息,最后由核心企业利用多源异构VIKOR方法对候选协同创新伙伴进行评价与排序,确定最佳协同创新伙伴。 科学构建协同创新伙伴指标体系是协同创新伙伴选择的关键。云制造模式下协同创新伙伴选择的前提是要了解协同创新伙伴对外合作情况、协同创新伙伴创新能力、协同创新伙伴技术方案,以及预计创新效果等诸多因素。一般而言,时间、质量、成本、服务和能力等因素是衡量合作伙伴的常见指标;云制造模式下合作伙伴选择的本质是选择一种云端服务,评价指标体系可参考服务平台的QoS指标,如价格、工期、可靠性、可用性及距离等[1];核心企业还需考虑合作伙伴评价的信誉度、可靠性、技术水平、交货期、价格、距离等指标[41]。此外,云制造环境下,合作主体分布广、差异大,核心企业与协同创新伙伴之间的经营理念、文化背景、规模大小、创新环境、沟通方式,以及两者之间的距离,都有可能影响协同创新效果,可见伙伴相容性也是选择协同创新伙伴的重要指标。本文借鉴已有文献研究成果,考虑协同创新伙伴的相容性,响应客户需求的时间、质量、成本、能力等多属性,构建基于相容性、创新能力、技术方案和创新效果4个一级指标的云制造协同创新伙伴评价指标体系。 每个一级指标又可细化为多个二级指标,每个二级指标都单独影响云制造模式下协同创新伙伴的选择。各一级指标具体细化为: (1)相容性指标细分为技术与资源互补适宜程度、伙伴与核心企业间营运政策的适宜程度、相对规模的适宜程度、协同创新伙伴与云制造核心企业的协同性、交流的便利性、云制造参与次数等。这些指标可以反映合作伙伴彼此间的适应程度,有利于后续协同创新稳健开展。 (2)伙伴创新能力指标可细分为技术水平、协同能力、创新资源、熟练程度、研发设备、管理制度和伙伴信誉等指标,可从不同方面反映出创新伙伴的研发能力,以及控制协同创新风险的能力。 (3)技术方案指标可细分为项目技术创新的难度、资金投入、创新成功概率、创新周期等指标,这些指标能反映出应用协同创新伙伴技术方案的成本与风险。 (4)创新效果指标可细分为成功盈利可能性、技术可靠性、技术可用性、技术被替代概率、产品投放市场的时间、预计市场占有率、新技术掌握的难易程度等,主要反映与伙伴合作后技术创新效果是否符合预期。具体指标及其释义如表1所示。 表1 云制造环境下协同创新伙伴评价指标体系 云制造协同创新伙伴多源异构评价信息主要由云制造环境下的核心企业决策者、相关领域专家和云制造平台等不同来源提供,评价信息包含实数、区间数、语言变量等多种结构形式。其中:①云制造参与次数、云制造创新成功的概率和技术被替代概率等指标的评价值可用实数表示;②技术创新所需资金投入量、创新周期、新产品投放市场时间和预计新产品市场占有率等指标,由于创新具有不确定性,此类评价信息采用区间数表示更合适;③技术与资源互补适宜程度、营运政策的适宜程度、相对规模的适宜程度、云端接入的便利性、技术水平、协同能力、创新资源、熟练程度、研发设备、管理制度、伙伴信誉、技术难易程度、技术创新成功盈利可能性、技术可靠性、技术可用性和技术服务人员对新技术掌握难易程度等指标采用语言变量来评价。 云制造环境下,当某云制造核心企业提出一项创新任务后,云制造平台将根据核心企业和创新任务的相关信息匹配出n个候选协同创新伙伴,记为x={x1,x2,…,xn}。在评价过程中,云制造核心企业根据相容性、创新能力、技术方案和创新效果等,形成以4个评价准则为基础的评价矩阵,可记为A={A1,A2,A3,A4}。由于信息来源的多样性以及信息形式的异构性,评价矩阵R=(rij)m×n中包含了实数、区间数、语言变量等多种评价值。评价矩阵的计算步骤如下: 步骤1获得实数。 云制造参与次数反映了合作伙伴参与协同创新的历史经验,可由云制造平台合作记录获得;创新成功概率主要根据候选合作伙伴过去参与云制造协同创新任务的反馈情况进行计算,即协同创新伙伴成功完成的创新项目数量相对于所承担云制造下创新项目数量的百分比(若无初始数据,其值可取50%);技术被替代概率是合作伙伴所用创新技术未来被新技术替代的概率,该指标值由专家和核心企业决策者共同评价。在这一步骤中,将获取的比率数据作为a15,a33的评价值,无需集结,a44的评价值由算术平均算子集结专家个人评价值而得到,上述评价值由评价矩阵R中的r15,r33和r44表示。 步骤2获得区间数。 合作伙伴提供的技术创新方案应包含创新项目资金投入和创新周期,核心企业一般都会邀请相关领域专家评价其数据的合理性并给出预期数;产品投放市场时间需要结合创新时间和生产组织时间,因此需要专家和核心企业决策者综合考察合作伙伴与核心企业的情况获得;预计市场占有率则需要由相关领域专家根据合作伙伴技术方案确定的新产品性能、成本、服务和同类产品情况等进行综合测评得到。由于这些指标受很多不确定因素影响,决策者无法准确给出指标值,故采用区间数表述更为科学。利用算术平均算子对多位专家给出的区间评价信息进行集结[42],得到指标a32,a34,a45和a46的评价值,上述评价值由评价矩阵中的r32,r34,r45和r46表示。 步骤3获得中智数。 一般而言,在过去的合作过程中,由合作企业对候选协同创新伙伴的感知和评价最为真实和客观,可由云制造平台记录核心企业对候选协同创新伙伴的技术水平、协同能力、创新资源、熟练程度、研发设备、管理制度、伙伴信誉等评价信息。而针对互补适宜程度、营运政策适宜程度、规模适宜程度、云端接入的便利性、成功盈利可能性、技术可靠性、技术可用性,以及掌握新技术难易度等指标值,可由核心企业组织内部或外部相关专家,对协同创新伙伴情况和技术方案进行评价,上述指标的评价信息为语言值。由于语言评价信息具有不确定性,需将其转化为具有真实程度、不确定程度和谬误程度的中智数,本文采用9个标度语言术语集,对应的单值中智数如表2所示[43]。 表2 语言变量与单值中智数 续表2 然后,根据语言术语评价值,将语言值转化为中智数。采用单值中智算术加权平均集结算子(式(5))对中智数进行集结。最终得到a11,a12,a13,a14,a21,a22,a23,a24,a25,a26,a27,a31,a41,a42,a43和a47等指标的评价值,上述评价值由评价矩阵R中的r11,r12,r13,r14,r21,r22,r23,r24,r25,r26,r27,r31,r41,r42,r43和r47表示。 TIAN等[44]指出,与模糊层次分析法相比,BWM方法的成对比较更少,且能获得更可靠的权重,因此,使用BWM方法来计算云制造协同创新伙伴一级指标的主观权重,并将该权重同等的赋予所属二级指标。具体步骤如下[45]: 步骤1确定决策指标集{c1,c2,…,cn}。其中n为最大准则数。 步骤2决定最好的(最重要的)指标和最差的(最不重要的)指标,分别记为cB和cW。 步骤3用1~9之间的数字来表达最好的指标对其他指标的重要程度(1表示同等重要,9表示相对极度重要),结果用向量AB=(aB1,aB2,…,aBn)表示,aBu表示最好指标B相对指标u的重要性,显而易见aBB=1。 步骤4用1~9之间的数字来表达其他指标对最差指标的重要程度(1表示同等重要,9表示相对极度重要),结果用向量AW=(a1W,a2W,…,anW)表示,auW表示指标u相对最差指标的重要程度,aWW=1。 对于每一组wB/wu和wu/wW,指标最优权重满足条件wB/wu=aBu和wu/wW=auW。为满足这两个条件,对于所有的u,差异绝对值|wB-aBuwu|和|wu-auWwW|的最大值要实现最小化。同时考虑权重的非负性加和为1,由此构建优化模型,如式(6): minmaxu{|wB-aBuwu|,|wu-auWwW|}。 s.t. wu≥0,对所有的u。 (6) 式(6)可以被转换为线性规划模型: minξL。 s.t. |wB-aBuwu|≤ξL,对所有的u; |wu-auWwW|≤ξL,对所有的u; wu≥0,对所有的u。 (7) 基于熵权法的客观赋权是利用信息效用的大小来反映指标的重要性,即评价信息熵客观决定各指标权重。为体现决策者对不同指标的重视程度,避免客观赋权未考虑决策者的主观偏好,利用主客观相结合的原则来计算指标权重。首先计算协同创新伙伴评价指标的熵权,然后将BWM计算得到的主观指标权重与评价指标的熵权结合起来,计算出指标的综合权重。 步骤1计算数值型指标的信息熵。 采用式(8)将评价矩阵R=(rij)n×m进行标准化,并将标准化矩阵进行正规化处理,得到规范化的数值型评价矩阵,记为R=(yij)n×m。 (8) 利用正规化实数数据所形成的矩阵,在有n个评价对象,m个评价指标(n,m)的评估问题中,求相关指标的熵权,其计算如式(9): (9) 步骤2计算区间值指标的信息熵。 首先利用式(10)对区间数进行标准化,得到标准化的区间值。 yij= (10) 式中:[aij,bij]为区间型评价值,bjmax=maxbij。 然后计算区间值指标的熵权,具体计算如式(11)[46]: (11) 步骤3计算中智数的信息熵。 中智数的标准化公式如式(12)[46]: yij= (12) 中智数的信息熵ej可以通过式(3)和式(4)计算得到。 步骤4计算各指标的熵权。 依据上述实数、区间数和中智数的熵权计算方法,可以得到各评价指标的熵权 步骤5计算评价指标的综合权重。 (13) VIKOR方法是一种折衷排序方法,适用于指标间不可公度或决策者无法准确描述偏好,但能接受妥协方案的情况,通过最大化群效用和最小化个体遗憾,对有限决策方案进行折衷排序[25]。本文采用VIKOR方法解决协同创新伙伴的选择问题,假设协同创新伙伴选择涉及k个决策者Zk(k=1,2,…,K),记为Ω={Z1,Z2,…,ZK},存在n个协同创新伙伴,记为X={x1,x2,…,xn}。由于云制造协同创新伙伴评价信息的异构,将评价指标集A={A1,A2,A3,A4}中的评价信息划分为3个子集O={O1,O2,O3},分别表示评价信息为实数、区间数和中智数的指标集。具体步骤如下: 步骤1建立并标准化评价矩阵。 根据3.2节和3.4节所介绍的内容,得到集结后的群决策评价矩阵及标准化矩阵yij。 步骤2分别计算正理想解(PIS)和负理想解(NIS)。 (14) (15) 步骤3计算Si,Ri和Qi的值[29],具体计算如式(16)和式(17): (16) (17) 其中:Si为群效用值;Ri为个人后悔值;Qi为折中排序指标;v为决策机制系数,v∈[0,1],v≻0.5表示依据最大化群效用的决策机制进行决策,v0.5表示依据最小化个体遗憾的决策机制进行决策,v=0.5表示依据决策者经协商达成共识的决策机制进行决策[25]。 步骤4对Qi按升序排序,记为A(1),…,A(i),…A(m)。如果A(1)满足评价指标C1和C2,则A(1)就是最优方案,Qi值最小。 C1:Q(A(2))-Q(A(1))≥1/(n-1); C2:根据Si,Ri和Qi的排序可知,A(1)的值最小。 云制造核心企业——某矿山装备制造公司根据客户要求,在半年内提供一款具有故障自诊断功能的新型地下矿山装备。该矿山装备不仅需要满足地下特殊作业环境,还需具备故障自诊断功能,且不同于核心企业已有定型产品。由于该装备创新涉及多个专业领域,且研制周期短,亟需多家企业密切合作,快速响应客户需求。为此,核心企业根据以往产品创新经验,迅速拟定分工合作方案,由自身承担矿山装备的整体功能设计与外观设计,新型钻具、液压系统、行走系统、故障自诊断系统和传感器等需要选择合适的协同创新伙伴来完成。本算例具体针对云制造核心企业选择故障自诊断技术研发制造协同创新伙伴进行分析。该核心企业向云制造平台提交故障自诊断技术研发需求后,平台经初步匹配筛选,推荐了x1,x2,x3,x4四位候选协同创新伙伴。核心企业通过云制造平台了解4位候选协同创新伙伴的基本情况、合作情况、历史评价记录等,核心企业组织专家评价协同创新伙伴的技术方案,并根据核心企业决策者的偏好等,得到包括相容性、研发能力、技术方案和创新效果等评价指标下的评价信息,由此获得评价矩阵R。 协同创新伙伴排序具体步骤如下: 步骤1建立规范化评价矩阵。 首先根据本文构建的评价指标,以及对候选协同创新伙伴的多方位了解,由云制造平台、核心企业和专家给出实数、区间数和语言值等多种异构评价信息。然后对这些多源异构评价信息进行集结,得到4位候选协同创新伙伴的综合评价值。协同创新伙伴定量指标和定性指标评价值的具体内容,分别如表3和表4所示。最后对评价信息进行正规化处理,可得到集结后的综合评价矩阵,如表5所示。 表3 协同创新伙伴定量指标评价值 表4 协同创新伙伴定性指标评价值 表5 规范化的决策评价矩阵 续表5 步骤2一级指标赋权。 根据BWM方法,对协同创新伙伴评价指标赋权。其中相对于其他一级指标而言,伙伴相容性A1的重要程度最低,创新效果A4重要程度最高。最重要和最不重要指标的比较向量,分别如表6和表7所示。其中:表6为最重要指标相对于其他指标的偏好程度,表7为其他指标相对于最不重要指标的偏好程度。 表6 最重要指标的比较向量 表7 最不重要指标的比较向量 根据式(6)与式(7),计算得到指标的权重向量w*=(0.476 2,0.285 7,0.127,0.111 1)和ξL*=0.095 2。 步骤3二级指标赋权。 根据3.4节介绍的综合指标权重方法,计算协同创新伙伴各评价指标的熵权,结合主观权重,可以计算各指标的综合权重,具体结果如表8所示。 表8 指标权重 步骤4计算各协同创新伙伴的Si,Ri和Qi值,并排序。 根据VIKOR方法在多源异构群决策中的应用,令v=0.5,分别计算4个协同创新伙伴的Si,Ri和Qi值,如表9所示。 表9 协同创新伙伴的Si,Ri和Qi值 由Qi值得到各候选协同创新伙伴的优先序为x3≻x2≻x1≻x4,其中协同创新伙伴x3的Qi值最小。根据VIKOR评价准则Q(A2)-Q(A3)=0.82>1/3,满足评价指标C1;协同创新伙伴x3在Si,Ri和Qi排序中,均为最小值,满足评价指标C2,由此可知,x3是核心企业最佳的协同创新伙伴。 在评价决策中,评价指标权重受到外界扰动而发生变化,可能导致候选协同创新伙伴的优先顺序也相应地变化。为检验本文方法的稳健性,对模型进行敏感性分析。通过调整测试指标权重,考察协同创新伙伴优先顺序的变化情况。具体对4个一级指标权重上下变动5%,10%,15%,20%,比较4位候选协同创新伙伴排序的变化。 (18) 求解φ=(1-ζwj)/(1-wj),由此得到不同权重的变化[32]。依次对权重wi上下变动5%,10%,15%,20%,再利用VIKOR方法得到相应的潜在合作伙伴的优先排序,共得到32个排序组合,排序结果变化情况如图2所示。 由图2可知,云制造模式下协同创新伙伴x3的Qi值在32次测试中均为最小,协同创新伙伴x4在32次实验中有4次排序发生变化,概率为12.5%。据此可知,当权重发生改变时,排序顺序有一定改变,但变化概率仅为12.5%,且最优伙伴x3的排序位置一直未发生变动。由此表明,在权重发生较大波动下,最适合核心企业的协同创新伙伴均为x3,同时说明该协同创新伙伴选择模型对权重的敏感性低,选择模型的稳健性较好。 本文针对云制造模式下协同创新伙伴选择过程中评价指标体系不完善、指标权重难以合理确定、多源异构评价信息处理难等问题,提出一种基于多源异构信息的VIKOR群决策方法,以更好地满足云制造模式下协同创新伙伴评价选择需求。总体而言,本文的主要工作如下: (1)本文构建了云制造协同创新伙伴评价指标体系。评价指标体系包括4个一级指标与23个二级指标,不仅考虑了云制造模式下核心企业与创新伙伴的相容性、协同创新伙伴的技术研发能力,还考虑了创新项目的技术方案及创新的预期效果等多因素,能更好地满足云制造协同创新伙伴选择决策的实际需要。 (2)对多源异构评价信息进行了有效集结。考虑了实数、区间数、语言值等多源异构评价信息,针对语言值采用中智数进行转换,避免信息丢失;根据各指标评价信息形式分类确定各指标的正负理想解,计算出折中排序指标,解决了多源异构信息不可公度性问题。 (3)提出了基于多源异构VIKOR群决策方法。将主观权重和客观权重相结合,避免了主客观赋权单独使用的缺点,为云制造企业协同创新伙伴选择提供了有效解决方案。通过进一步实证分析、灵敏度分析,以及对比分析,验证了基于多源异构评价信息的VIKOR群决策方法适用于云制造企业协同创新伙伴评价选择情境,其评价决策结果更加稳健与准确,可为云制造企业选择协同创新伙伴提供可靠的决策参考。 本文主要采用实数、区间数和语言变量等评价信息,现实中受云制造环境及协同创新伙伴的影响,评价信息形式可能呈现出多样性和动态性,未来可以进一步探讨语言变量为直觉模糊集、区间语言直觉模糊集、犹豫模糊语言集等形式,从而更好地适应云制造环境下协同创新伙伴选择的需要。
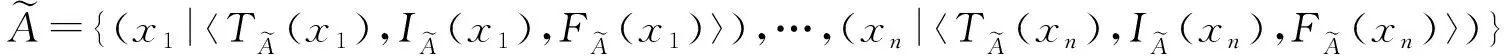
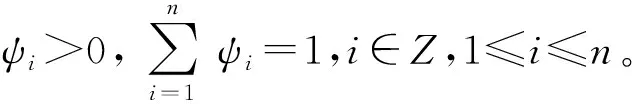
3 云制造协同创新伙伴选择模型
3.1 评价指标体系
3.2 评价矩阵


3.3 主观赋权
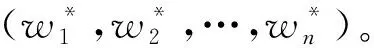

3.4 综合赋权


3.5 VIKOR方法排序
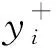

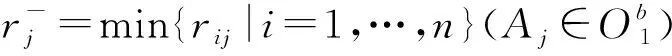
4 云制造协同创新伙伴选择算例分析
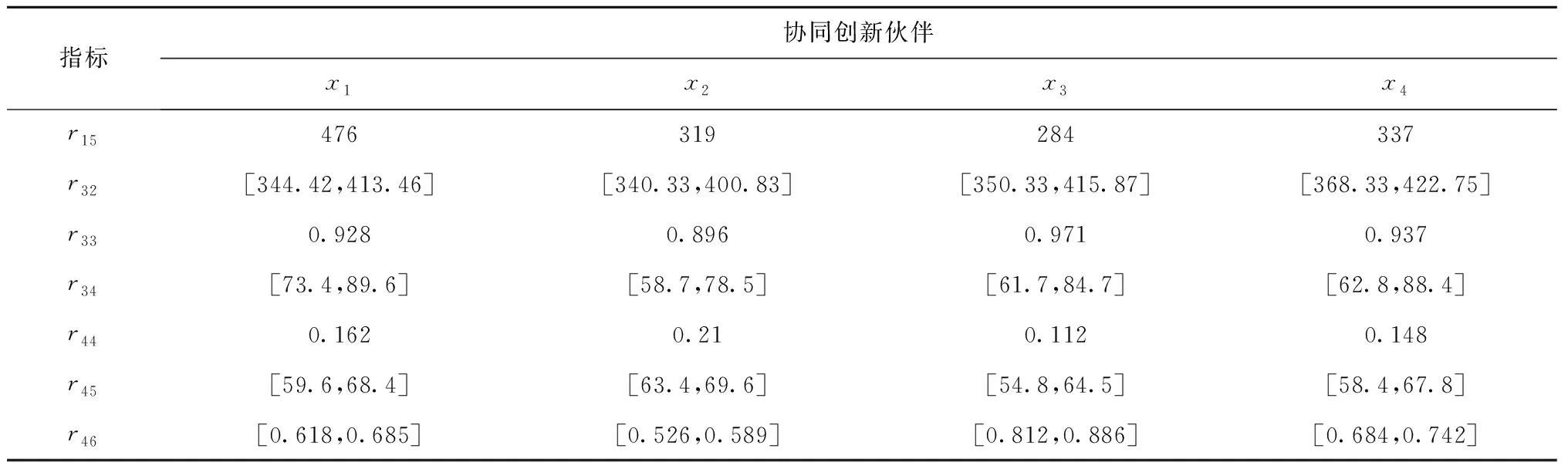
4.1 协同创新伙伴排序




4.2 敏感性分析
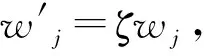
4.3 比较分析

5 结束语
