环境激励下基于波动能量法的结构损伤识别
2022-02-19李旭,谢艳,殷翅,常军
李 旭,谢 艳,殷 翅,常 军
(苏州科技大学土木工程学院,江苏苏州 215011)
引言
目前土木工程结构的健康监测方法大多基于检测结构模态参数(频率、阻尼和振型)的变化[1],这些变化是全局性质,取决于结构整体特性的变化,因此,当损害局部化时,其几乎没有变化。而且其对环境(例如温度)和边界条件的变化(例如土壤-地基系统)敏感,在实际操作中难以分离环境影响,从而导致识别结果不精确。相比之下,波动方法是基于结构响应分析的波传播方法,作为模态叠加的替代方案,结构的响应可以表示为通过结构传播的波的叠加,从其外部和内部边界反射并干涉。由局部损坏引起的刚度损失将导致通过损坏部分的波传播延迟,这可以使用沿着波路径记录在受损区域的每一侧上的响应数据来检测。此外,波传播时间的局部变化对土-结构相互作用的影响不敏感,这是基于检测结构频率变化的模态方法的主要障碍[2]。
基于波动理论的结构损伤识别方法因其物理概念明确、敏感性高和识别直接等优势而越来越受到青睐。1999年,SAFAK 等[3]提出了一种分层连续模型,用于分析建筑物的地震响应,并通过追踪不同层中参数的变化来检测损坏;2003 年,MA 等[4]提出了一种基于集总质量建筑模型通过波传播识别损伤的方法,并在模拟的建筑响应数据上进行了测试;2003年,OYUNCHIMEG 等[5]将归一输入输出最小化(NIOM)方法应用于洛杉矶地区建筑物所记录的地震响应数据,准确给出了结构的脉冲响应函数;2006年,SNIEDER 等[6]对建筑物记录不同层的响应信号进行反卷积,分离了土壤对建筑物响应的影响,使得建筑物响应只与建筑物材料性能有关;2008 年,TODOROVSKA 等[7]对一个七层建筑物在地震作用下的响应数据进行反卷积分析,得到了结构的一阶频率并对结构整体及局部进行损伤识别,识别结果表明与实际探查到的损伤情况一致;2013年,NAKATA等[8]利用反卷积干涉法对建筑物的响应进行分析,得到了波速及质量因子及虚源位于建筑物任意一层的情形;2015 年,EBRAHIMIAN 等[9]研究了Timoshenko 梁中波的传播情况,相比剪切梁,Timoshenko梁更真实的模拟了建筑物的响应;2017年,马占雄[10]用两种梁模型来拟合结构的动力反应,通过最小化模型与实际结构之间的误差来识别结构波速,进而识别结构损伤。
以上研究成果主要用于地震作用下的结构损伤识别,环境激励下基于波动理论的损伤识别方法未见文献。为此,论文从波动理论出发,利用环境激励基于结构中波能量的变化来对结构进行损伤识别,通过S 变换分析结构输出响应信号,进而通过脉冲响应函数得到结构各层之间的波传播时间,构建了基于波能量的损伤指标,识别结构的损伤位置与损伤程度。
1 S变换与脉冲响应函数
波动理论的本质是足够长的波将离散的介质视为“连续体”传播[11]。在狭窄的建筑物中,主要发生剪切变形,可以将由于地震引起的变形建模为一维波传播,最简单的模型就是等效的均匀剪切梁模型。在实际建筑物中,通常将其简化为一个下端固定的剪切梁模型如图1 所示,底部输入的波将向上传播,由于建筑物材料的阻尼及各层边界的反射,使得在建筑物不同高度观察点处会发现波的延迟及衰减。经过在建筑物中的多次反射,由相长干涉产生的运动将主导响应,为了测得建筑物不同层间波传播时间的延迟,采用脉冲响应函数法。

图1 剪切梁模型示意图Fig.1 Schematic diagram of the shear beam model
1.1 S变换
S 变换是针对非平稳信号的时频分析方法,其结合了小波变换与短时傅里叶变换的优势,其高斯窗函数与频率的倒数成正比,免去了窗函数的选择,从而解决了窗宽固定问题,可自适应调节分辨率且其逆变换无损可逆,避免了小波变换中基函数的选取,从而更精确地分析非平稳信号和局部特征。信号u(t)的S变换如式(1)所示。
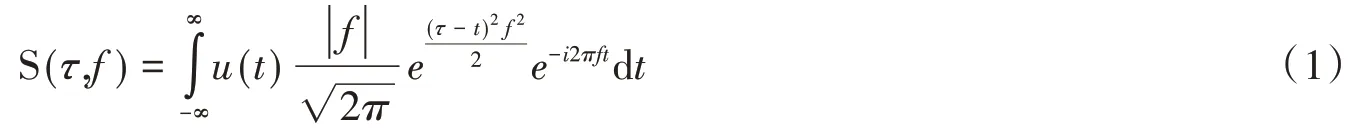
式中:t是时间;f是频率;τ是控制高斯窗口时间轴的位置参数。
1.2 脉冲响应函数
将建筑物视为线性时不变系统,在底部输入一个地面运动uref(t),那么在建筑物的每层都有相应的输出响应ui(t)。输入和输出在时域中通过式(2)相关联:
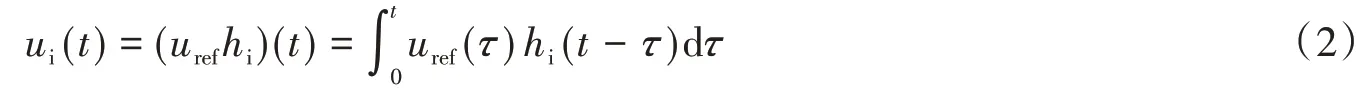
在频域中有:

式中:*表示卷积;函数hi(t)是脉冲响应函数,表示在i级对输入的响应。建筑物在不同高度得到的脉冲响应函数表明了施加在参考点处的虚脉冲是如何在结构中传播;函数是传递函数,式(3)表示频域内在i级的响应和输入之间的函数运算。故对任意层的输出响应进行S变换,并代入式(3)可得:

由于Sref(τi,ω)在某些点出可能为零从而导致式(4)不成立,故改进的传递函数如式(5)所示。

在线性系统中,传递函数是脉冲响应函数的傅里叶变换。

因此,可以通过相应的传递函数进行傅里叶逆变换,从记录的响应中得到脉冲响应函数,用于模拟虚脉冲在建筑物中的传播,然后利用脉冲响应函数来测量时间延迟。脉冲响应函数可以通过式(7)计算求得。

2 波能量
弹性波在介质某一点单位体积内激起的全部能量(包括动能和势能)称为波动的能量密度[12]。以一维剪切波为例,单位体积内的动能与势能分别为:

式中:μ为剪切模量;ρ为质量密度。对于单一方向传播的行波u=f(x-ct)或u=g(x+ct),由于波动自变量对时空坐标的耦合,存有:

将式(10)代入式(8),并且波速c=,可得:

即介质单位体积内的动能和势能恒相等。所以波的能量密度W为:

因此,波在传播过程中的总能量E为:

式中:W为波能量密度;V为波穿过结构的体积;t为波在结构中的传播时间。
在以剪切变形为主的结构动力响应中,波在每层的传播时间为:

式中:h为结构每层层高;c为波在结构中的传播速度;K为结构刚度;M为结构质量。
因此,当结构发生损伤时会导致波在结构中传播时间的延迟,从而使得在损伤处所消耗的波动能量的增加,故论文以刚度折减代表结构损伤,以式(7)求得的时间t为传递量,定义基于损伤的波动能量的损伤指标η为:
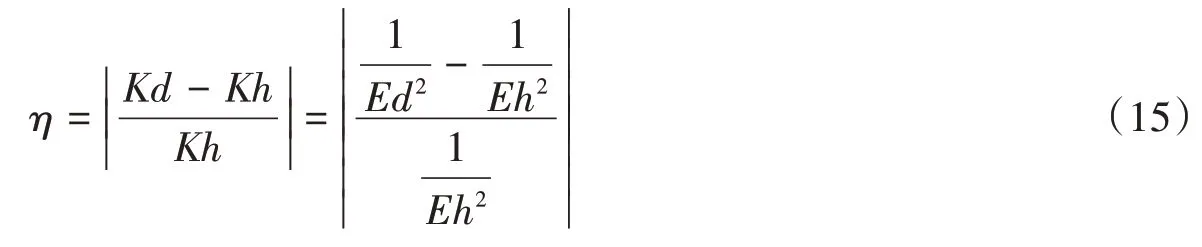
式中:Ed和Eh分别代表结构损坏状态与结构完好状态下的波的能量。整体识别流程如图2所示。

图2 损伤识别流程图Fig.2 Damage identification flow chart
3 试验分析
为了验证损伤指标的有效性,对图3所示的三层钢框架进行随机振动试验,试验中设置结构未发生损伤和第二层刚度折减20%两种情况。该框架高0.45 m,宽0.4 m,每层都布置了加速度传感器,采样频率为1/0.001 95 Hz。第0 s开始采集信号,第12 s开始振动,第90 s结束振动。

图3 三层钢框架试验Fig.3 Three-story steel frame test
采集未损伤状态下第一层至第三层的加速度响应信号图4所示。
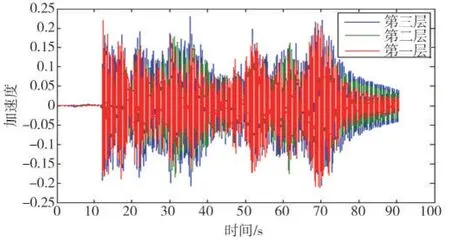
图4 各层加速度响应信号Fig.4 Acceleration response signal of each layer
由于受试验结构高度与传感器型号的限制,导致采集的加速度信号与识别所需的时间精度相差较大,而基于脉冲响应函数的波传播时间t为时间间隔的整数倍,故论文中采用了线性插值的方式来人为增大数据的采样率,插值过后的数据采样频率为1/0.000 032 5 Hz,满足识别精度要求。在实际结构中,由于结构高度的增大对采样频率的要求会大大降低。
将线性插值过后的各层加速度响应信号进行S 变换代入式(7),取第三层为参考点,求各层相对于第三层脉冲响应函数峰值的偏移时间,结构未发生损伤时,各层脉冲响应函数如图5所示。
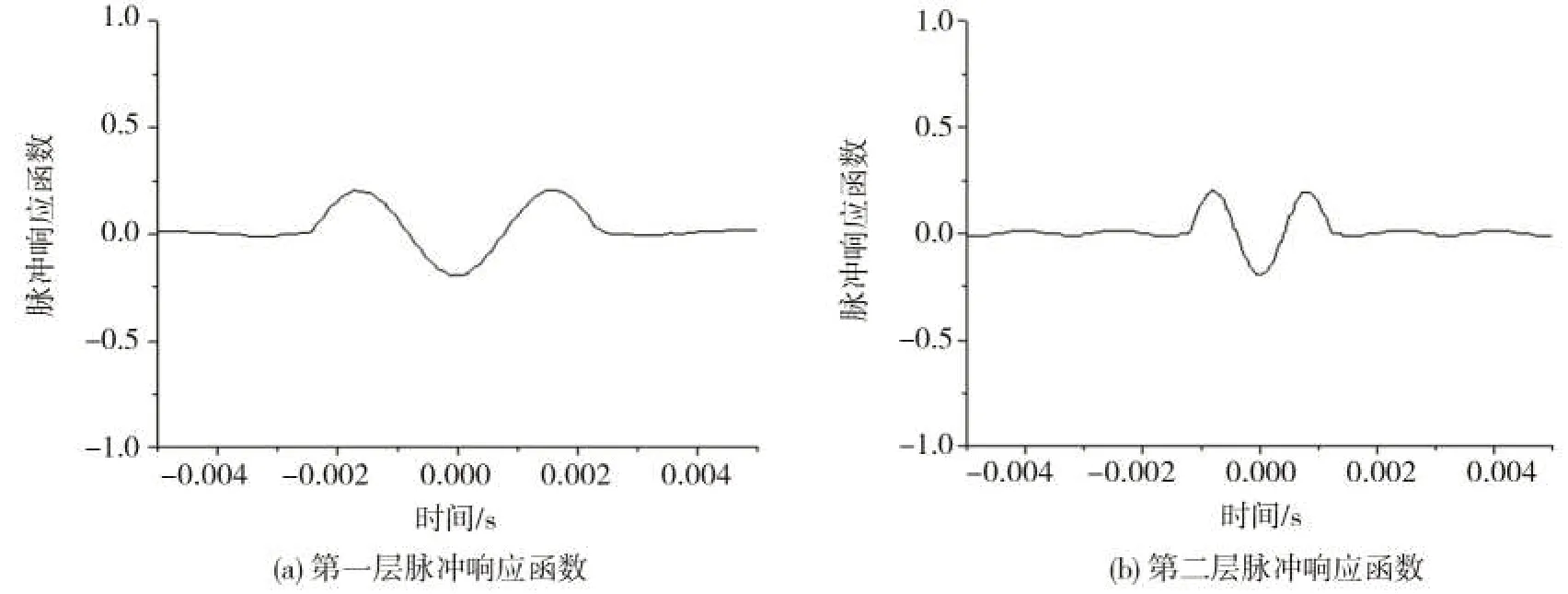
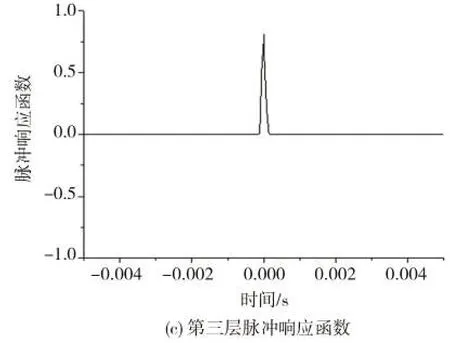
图5 各层脉冲响应函数Fig.5 Impulse response function of each layer
将求出的各层脉冲响应函数峰值的偏移时间代入式(13)及式(15),求得波在传播过程中的能量及损伤指标η,识别结果见表1。

表1 未损伤试验识别结果Table 1 Undamaged test identification results
当结构第二层发生损伤时,识别步骤与上述相同,识别结果见表2。

表2 损伤20%试验识别结果Table 2 Recognition result of damage 20%test
分析试验的识别结果可知:当结构未发生损伤时,损伤指标η值约在3%,而当结构第二层损伤20%时,损伤指标的值约为18%,结果表明:论文提出的方法能够识别出结构损伤,最大损伤误差约在3%,分析误差原因可能为受试验框架层高影响,导致所需采样频率较大使得记录的响应不能满足其精度要求,且记录的响应亦受环境影响,为验证误差原因,论文进一步采用数值模拟对识别方法进行验证。
4 数值模拟
为了进一步验证损伤指标识别结构损伤的精确性,建立了六层弹性分层剪切梁有限元模型,由弹性半空间支撑,垂直输入平面剪切波激励,如图6 所示。主要参数为:每层高3 m,宽6 m。弹性模量2 × 1011Pa,泊松比0.3,密度7 800 kg/m3。

图6 六层弹性分层剪切梁模型Fig.6 Six-layer elastic layered shear beam model
对弹性分层剪切梁模型输入白噪声激励,模拟环境激励信号。采样频率为10 000 Hz,激励时长10 s,输入信号见图7。
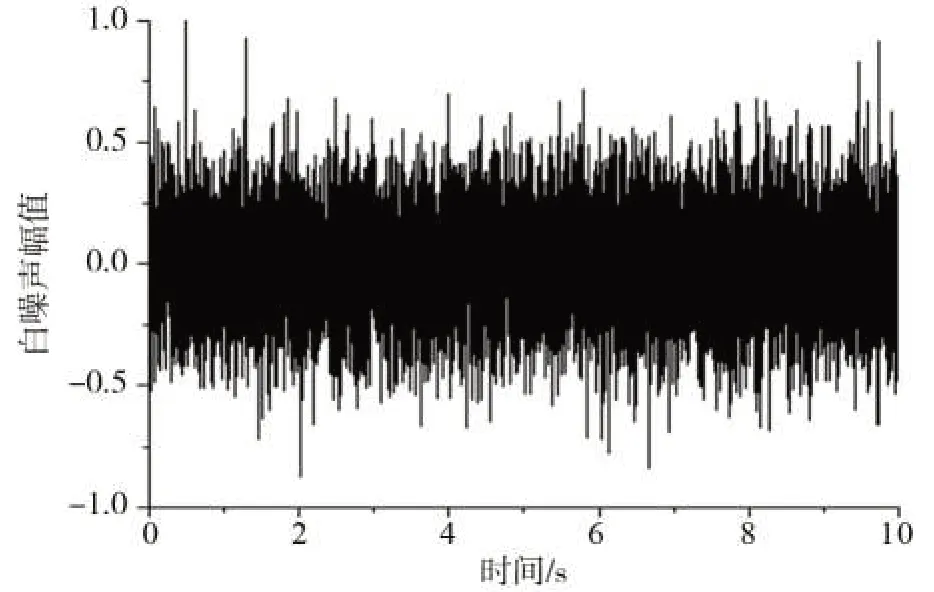
图7 输入信号Fig.7 Input signal
为了验证损伤指标能够识别损伤位置与损伤程度,定义四种损伤工况见表3。

表3 不同损伤工况Table 3 Different damage conditions
对于工况一刚度损伤10%,采集环境激励下结构1~6号节点位移时程信号见图8。

图8 工况一1~6号节点位移时程曲线Fig.8 No.1-6 node displacement time history curve of No.1 condition
对1~6节点的位移时程信号采用式(7)进行计算得到一至六层的脉冲响应函数见图9。
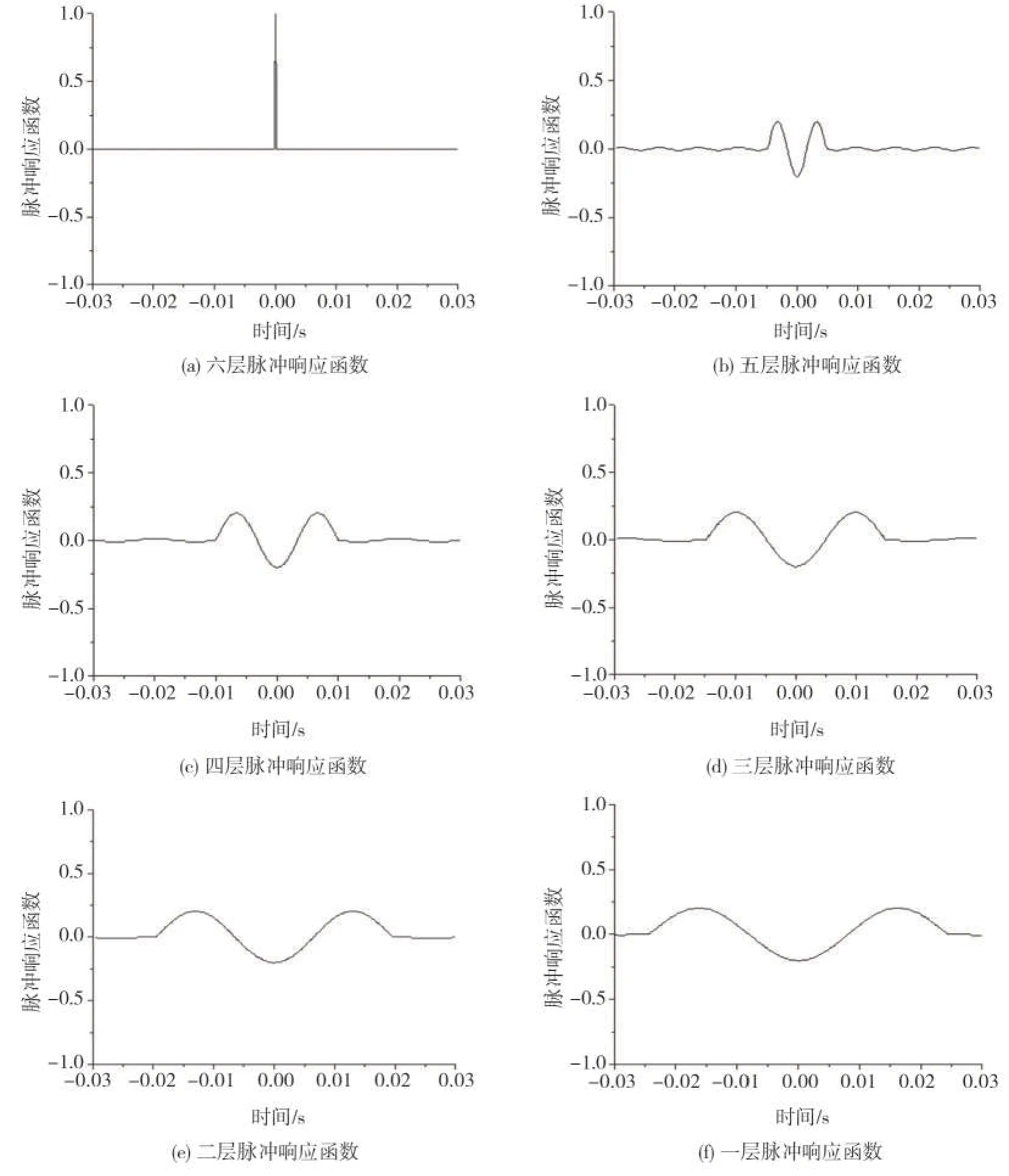
图9 1~6层脉冲响应函数Fig.9 1-6 layer impulse response function
取顶层作为参考点,即假设在顶层输入单位虚脉冲,进而求解出其他各层相对于顶层的脉冲峰值偏移时间即波在各层的传播时间,再由式(12)和式(13)计算得到完好状态下的
波动能量Eh和损伤状态下的波动能量Ed,最后代入式(15)得到损伤指标见表4。

图10 工况一的识别结果Fig.10 Recognition result of working condition one
从图9-10 和表3 可以看出:结构的第三层刚度下降10%时,第三层脉冲曲线峰值的偏移时间与其它层相比变大,从而导致损伤能量值变大。第三层的损伤指标增大到11%,说明第三层的损伤能量增大和刚度下降,以上情况符合设定的工况,说明损伤指标对结构损伤位置的敏感性较好,并且当损伤程度在20%及40%时,虽其余各层也存有少许损伤,但损伤程度大约在5%,相当于没有损伤,这与模拟的工况一相一致。
为验证损伤指标的精确性,采用文献[13]所提出的模态识别方法来识别工况一的结构损伤,求得结构的Pk(损伤程度)与k′f(频率平均斜率),见表5。

表5 模态识别结果Table 5 Modal method recognition results
从表5 可以看出:对于损伤40%的工况,模态法的识别结果较为精确,但对于损伤10%的工况,模态法识别精度较差,相比之下,基于波动能量的识别方法能更好地识别出小损伤。
因此,当结构发生不同程度的单个损伤时,损伤指标能精确的识别损伤位置与程度,且能识别小损伤。
从图11和表6可以看出:结构的第二层和第四层发生了损伤,损伤程度大约在20%和40%,其余各层也存有少许损伤,但损伤程度大约在5%,相当于没有损伤,这与模拟的工况二相一致。
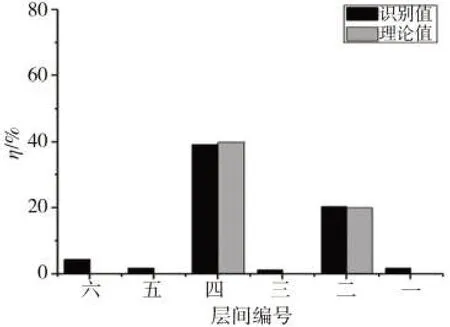
图11 工况二的识别结果Fig.11 Recognition result of working condition two
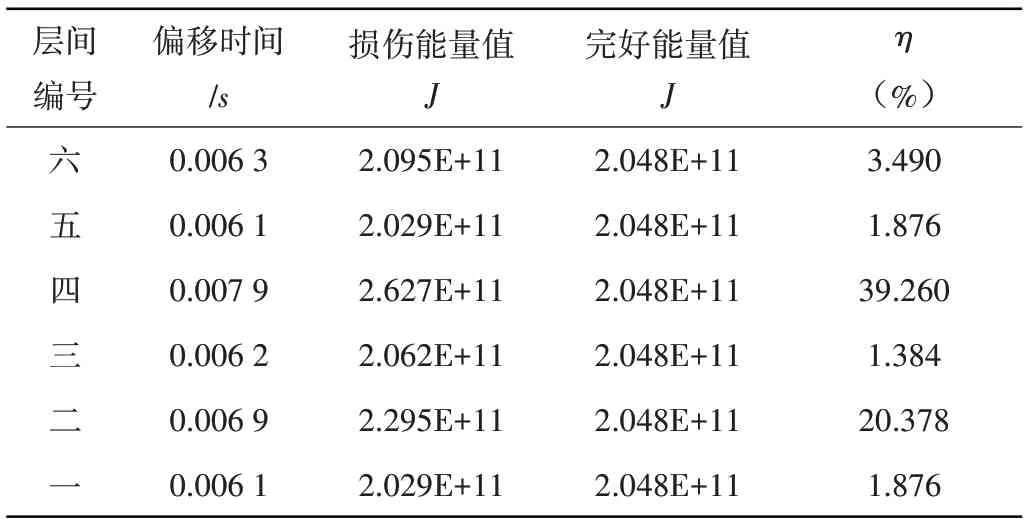
表6 工况二的识别结果Table 6 Identification result of working condition two
从图12和表7可以看出,结构的第一层、第三层和第五层发生了损伤,损伤程度大约
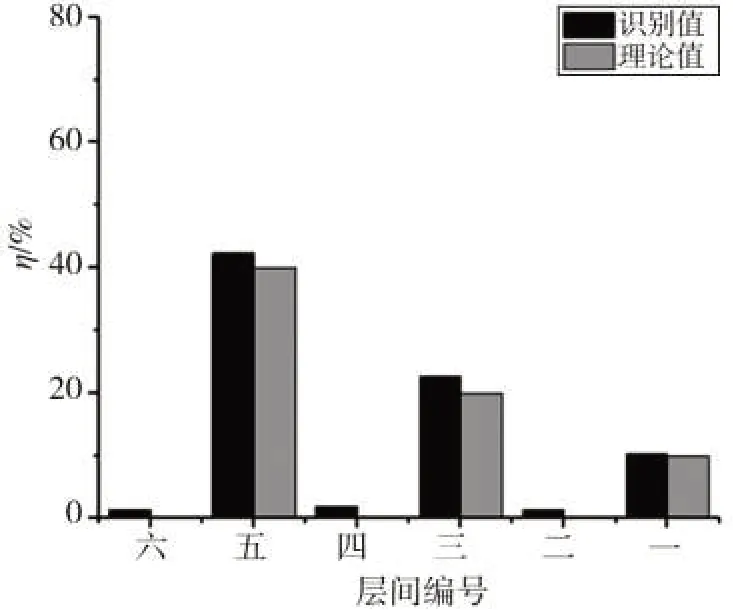
图12 工况三的识别结果Fig.12 Recognition result of working condition three
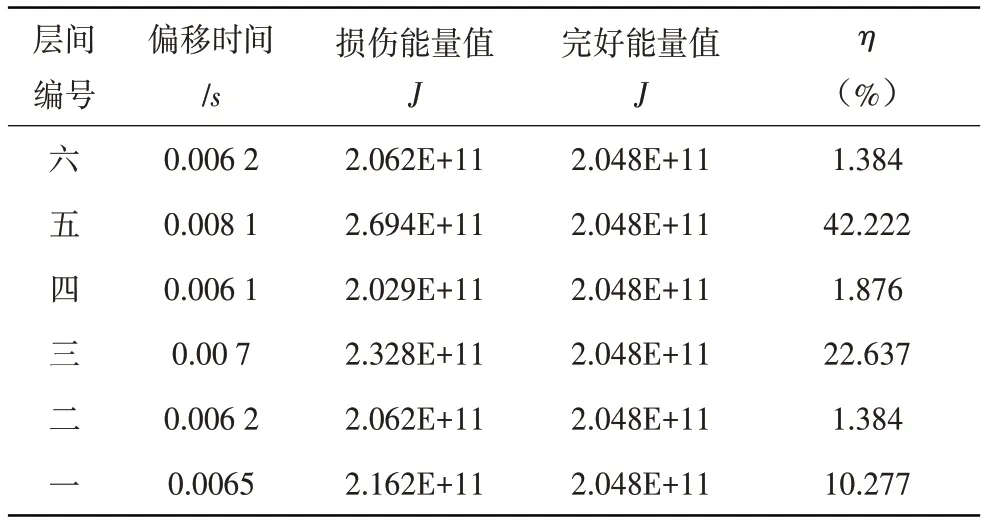
表7 工况三的识别结果Table 7 Identification result of working condition three
在10%、20%和40%,其余各层也存有少许损伤,但损伤程度大约在5%,相当于没有损伤这与模拟的工况三相一致。
比较工况二与工况三,当结构在不同位置发生不同程度的多处损伤时,损伤指标能够精确地识别出结构损伤位置与程度。
从图13和表8可以看出:识别出的损伤指标值都很小,相当于没有损伤,与模拟的工况四相一致。对比无损伤状态下的试验与数值模拟可知;数值模拟下损伤指标的识别精度较高,与试验的误差分析推断相一致,试验中受试验框架高度和环境影响使得损伤指标的识别值出现误差,但总体上符合试验误差范围。
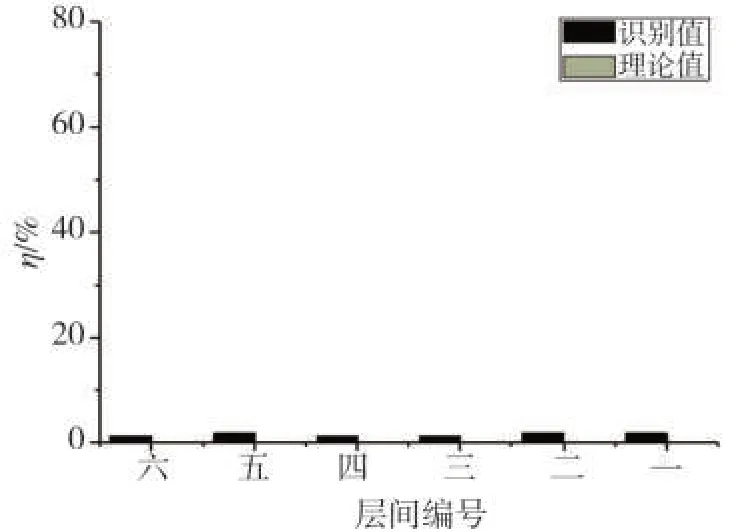
图13 工况四的识别结果Fig.13 Recognition result of working condition four
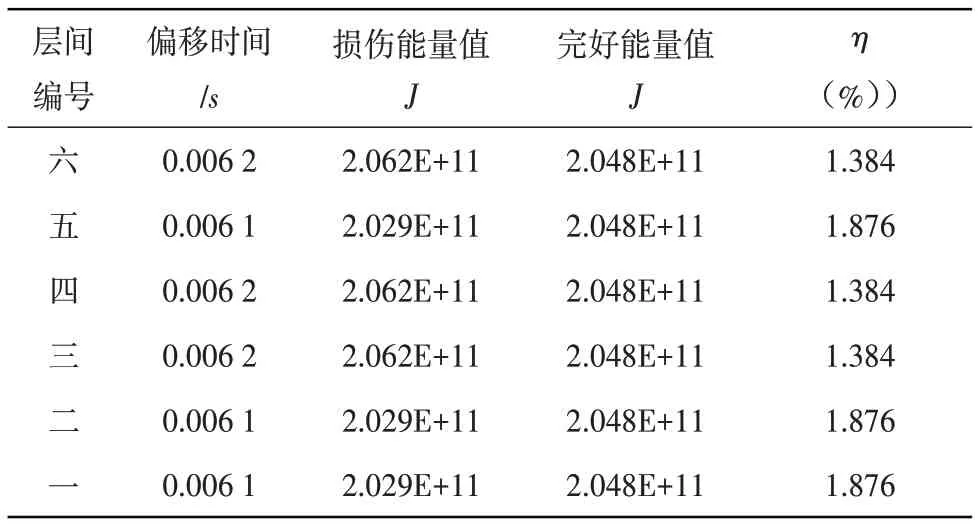
表8 工况四的识别结果Table 8 Identification result of working condition four
综上所述,结合试验与数值模拟验证,基于波能量的损伤指标能够识别结构单点及多点损伤的位置与损伤程度,且识别精度较高。
5 结论
基于其敏感直接的优势,波传播方法能够较精确地识别结构的局部损伤。作为时频分析方法的S 变换能很好地分析非平稳信号,进而解决环境激励下识别精度不高的问题。论文采用S 变换分析了结构响应信号,构建了基于刚度的波能量损伤指标,并将其应用于试验及数值模型,得到了理想的结果,并获得了如下结论:
(1)相比模态识别方法,基于刚度的波能量损伤指标能够精确识别结构是否损伤、损伤位置及损伤程度;且不仅可以识别单点损伤,还可以识别多点损伤且不受损伤位置的限制。
(2)S变换解决了环境激励下非平稳信号的问题,使得环境激励下基于波动能量的识别结果更精确。
(3)该研究成果为实际工程中的结构损伤识别应用提供支持。
